Prova orale concorso ordinario
Candidato: Milo Viviani
Classe di concorso: A026 - Matematica
Traccia
Geometria analitica nello spazio: Condizioni di parallelismo e perpendicolarità tra retta e piano e loro posizione reciproca
La classe
Indirizzo: Liceo Scientifico Tradizionale
Anno: II anno II biennio (IV anno)
Rifermento normativo: Indicazioni nazionali riguardanti gli obiettivi specifici di apprendimento (DPR 89/2010)
Composizione classe: 20-25 alunni e alunne, con possibili casi di DSA discalculici (107/2010)
TIC
Geogebra: - costruzione retta e piano nello spazio
- studio delle posizioni reciproche tra retta e piano nello spazio
-Lezioni frontali
-Esercizi svolti
- Strumenti digitali
-BYOD
Metodologie
Obiettivi specifici di apprendimento
-
CONOSCENZE: piani e rette nello spazio, loro posizioni reciproche, perpendicolarità e parallelismo
-
ABILITÀ: scrivere le equazioni di un piano e una retta nello spazio, determinare le loro posizioni reciproche
- COMPETENZE: applicare gli strumenti della geometria analitica e dell'algebra lineare per studiare la disposizone di rette e piani nello spazio
Programma lezioni
Lezione 1. Richiami di geometria analitica euclidea nello spazio
Lezione 2. Richiami di algebra lineare e condizioni di parallelismo e perpendicolarità tra retta e piano nello spazio
Lezione 3. Studio delle posizioni reciproche retta-piano
Lezione 4. Verifica competenze acquisite
Prerequisiti
-
Calcolo algebrico e polinomi
-
Geometria analitica nel piano
-
Geometria euclidea nel piano
-
Sistemi di equazioni lineari
- Calcolo vettoriale e matriciale
Differenziazione obiettivi di apprendimento
-
Livello alto: analizzare in dettaglio i casi degeneri delle equazioni studiate sia analaticamente che con GeoGebra
-
Livello base: assimilare e risolvere semplici esercizi inerenti al materiale presentato
- DSA discalculici: risolvere e interpretare le equazioni attraverso il solo utilizzo di GeoGebra
Lezione 1
L'equazione della retta nel piano \(Oxy\)
Formula in coordinate cartesiane
Retta passante per due punti \(P,Q\)
Formula parametrica, di parametro \(t\in\mathbb{R}\)
L'equazione della retta nello spazio \(Oxyz\)
Formula in coordinate cartesiane: intersezione di due piani
Retta passante per due punti \(P,Q\)
Formula parametrica, di parametro \(t\in\mathbb{R}\)
L'equazione della retta nello spazio \(Oxyz\)
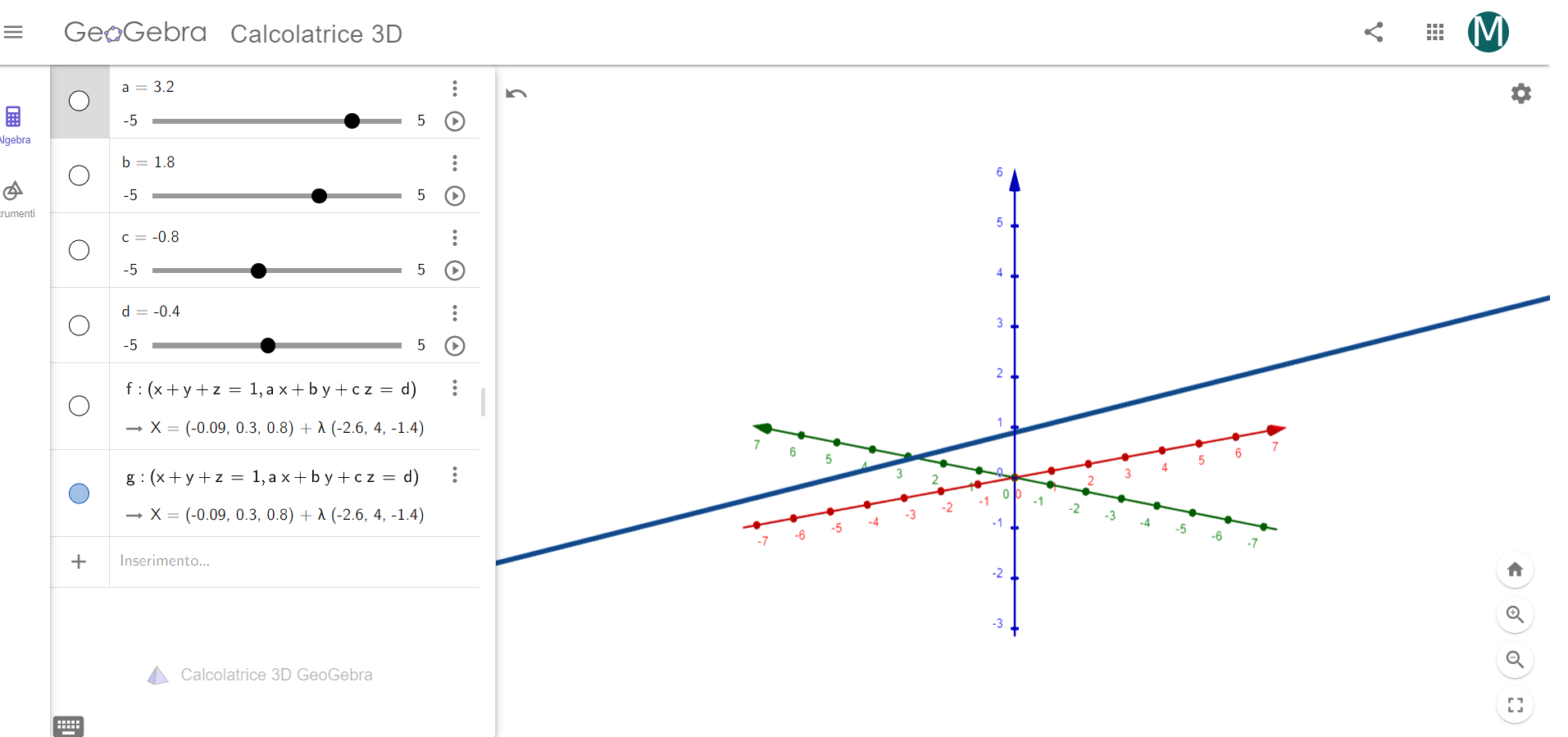
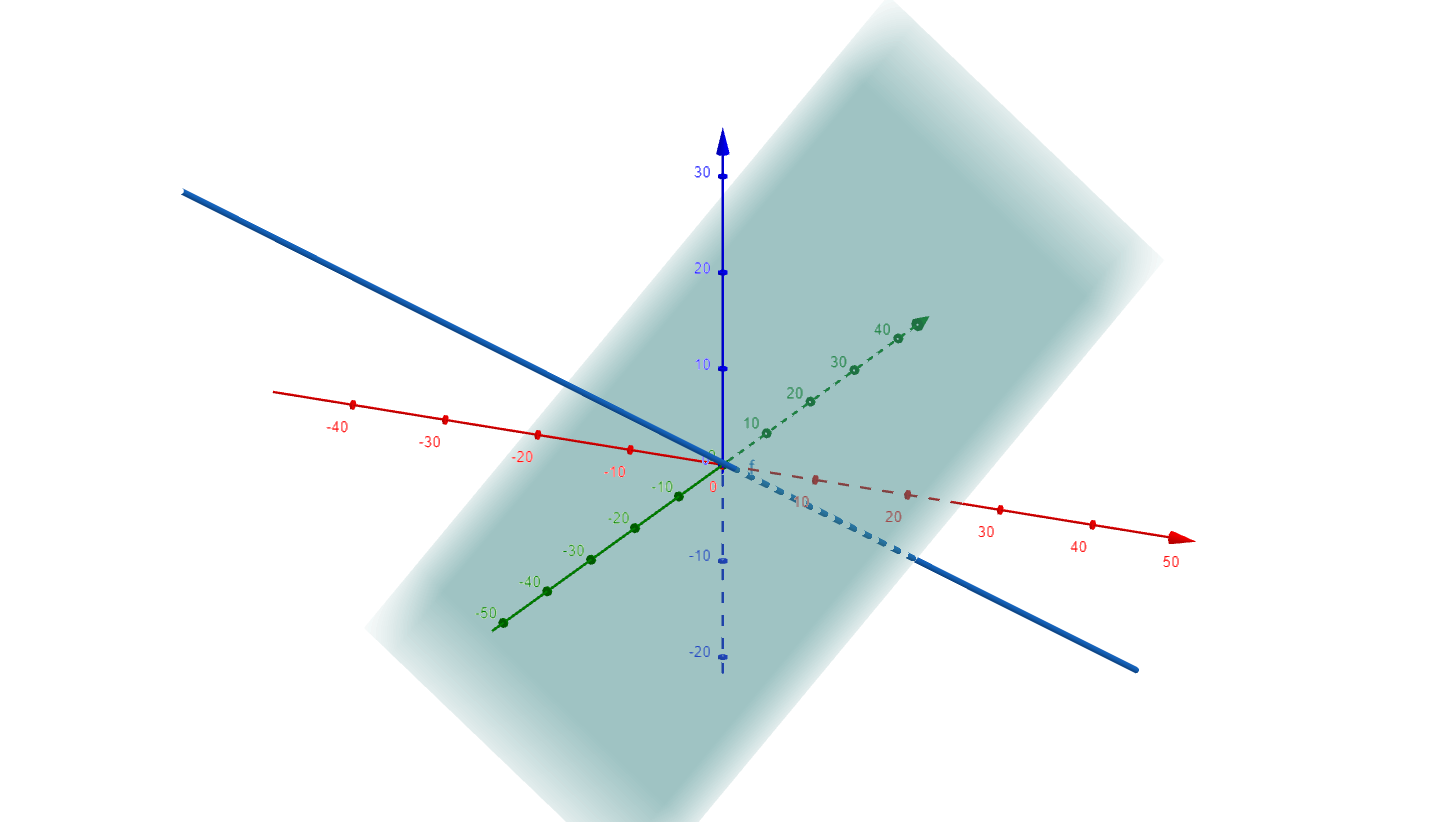
L'equazione della retta nello spazio \(Oxyz\)
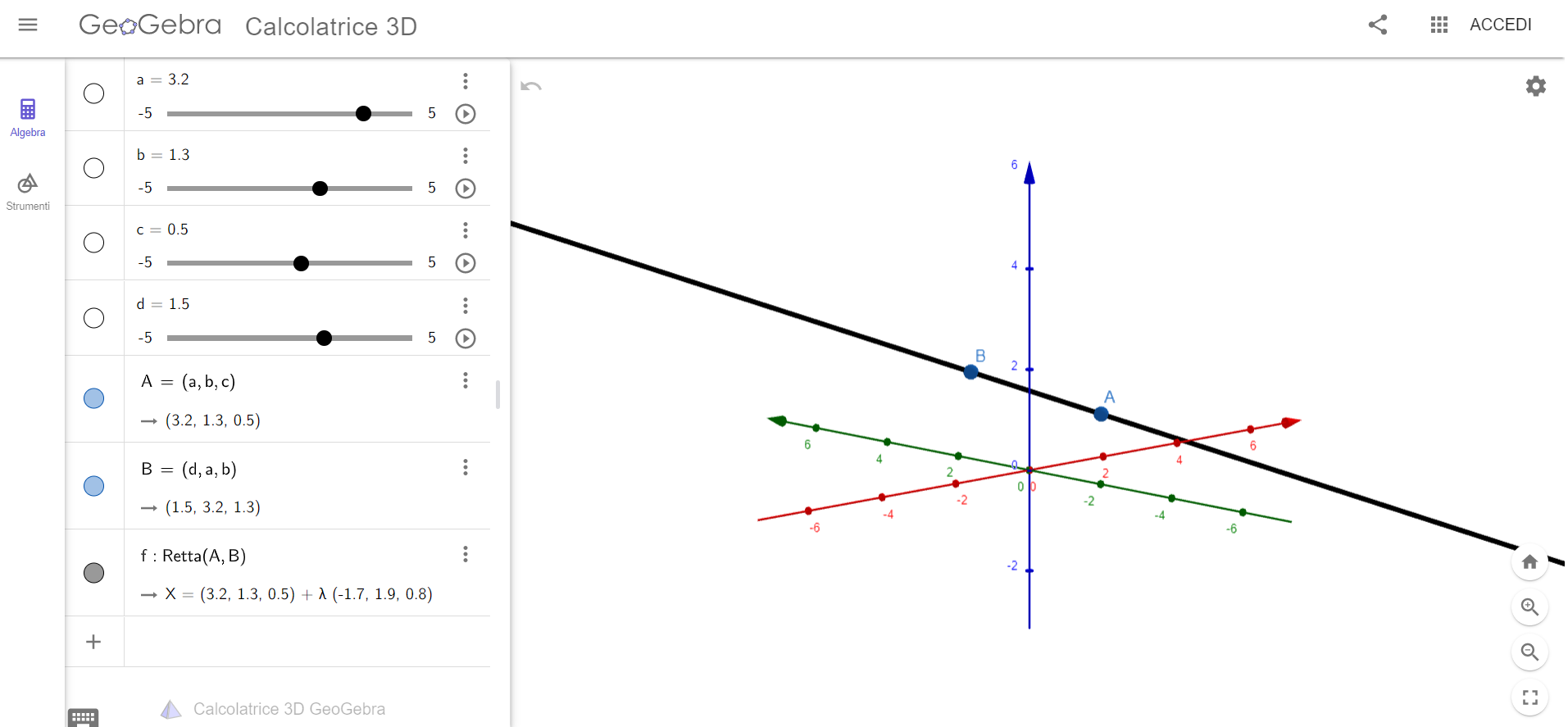
L'equazione del piano nello spazio \(Oxyz\)
Formula in coordinate cartesiane
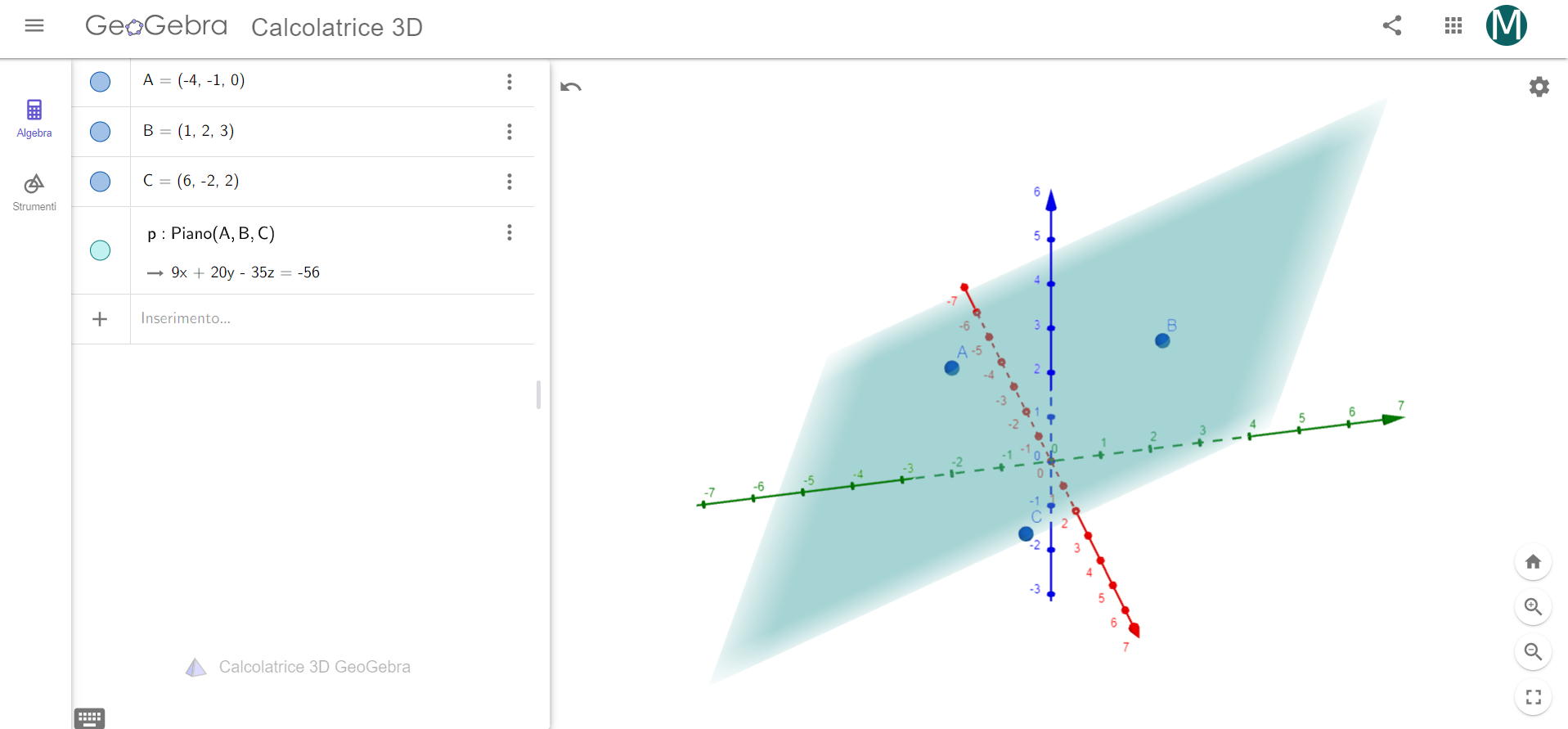
Piano passante per tre punti \(P,Q,R\)
Formula parametrica, di parametri \(t,s\in\mathbb{R}\)
L'equazione del piano nello spazio \(Oxyz\)
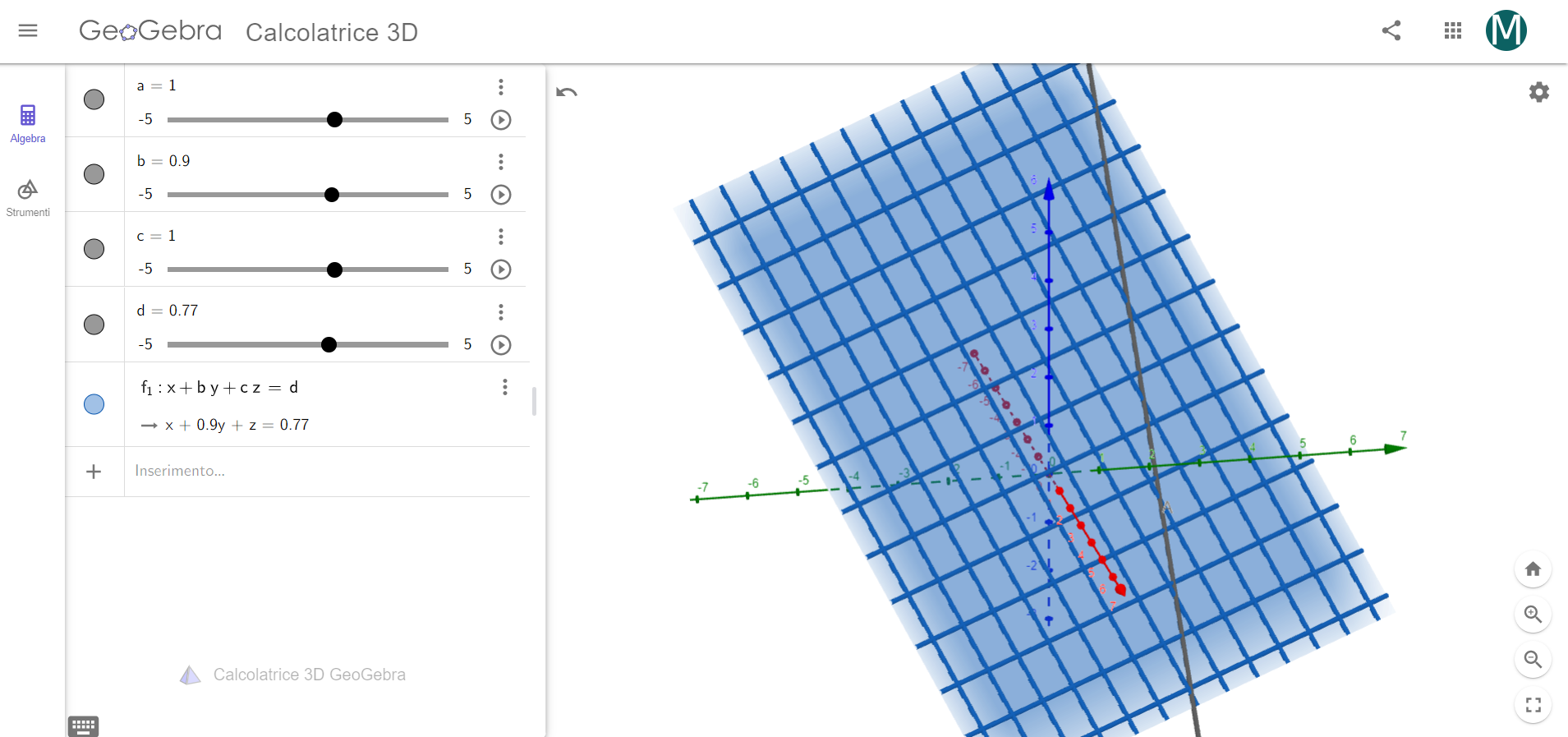
L'equazione del piano nello spazio \(Oxyz\)
Piano passante per tre punti \(P,Q,R\)
Lezione 2
Rette parallele nel piano \(Oxy\)
sono parallele se e solo se
Due rette nel piano in coordinate cartesiane
sono paralleli
Rette perpendicolari nel piano \(Oxy\)
sono perpendicolari se e solo se
Due rette nel piano in coordinate cartesiane
sono perpendicolari
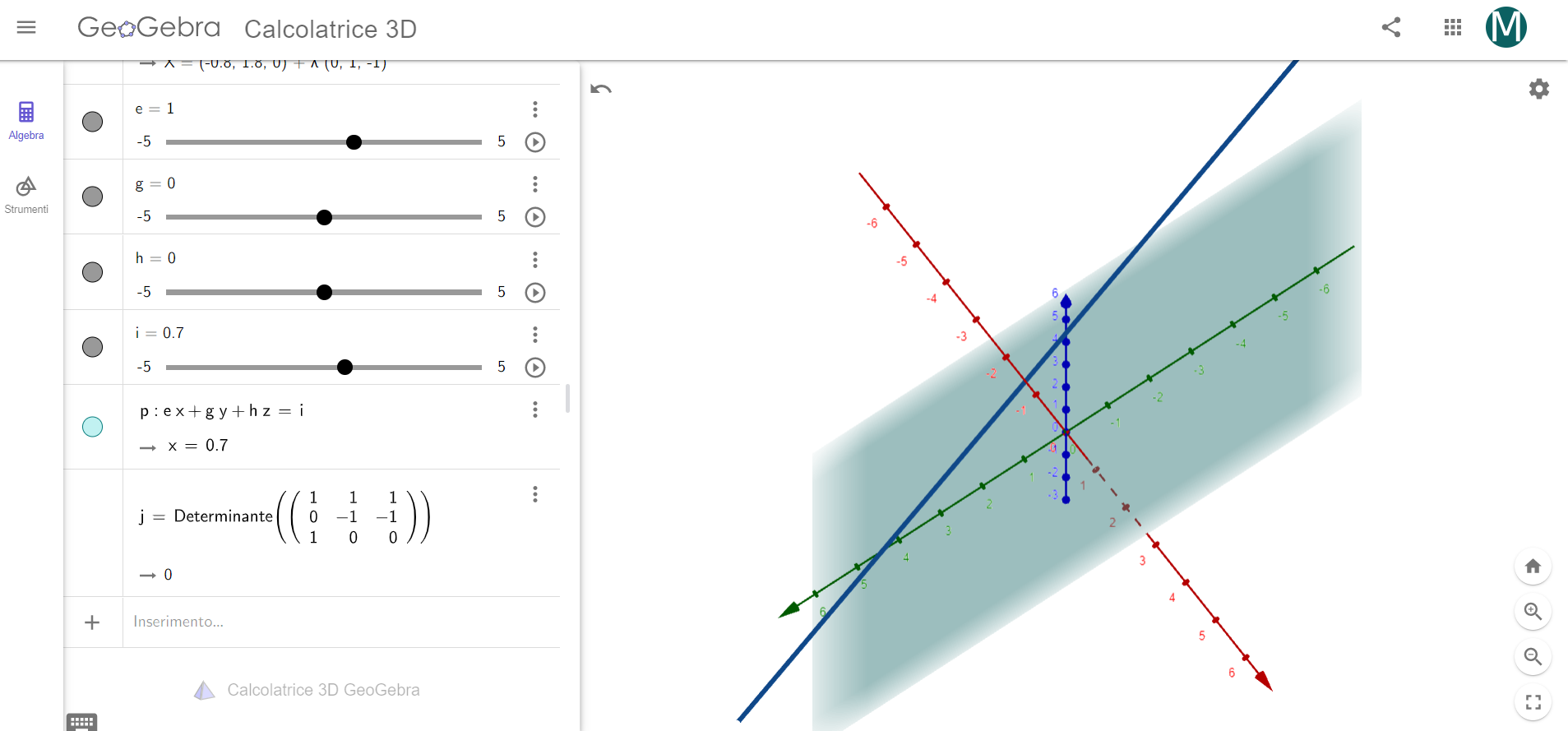
Retta parallela ad un piano nello spazio \(Oxyz\)
sono paralleli se e solo se
Una retta
e un piano nello spazio in coordinate cartesiane
Retta parallela ad un piano nello spazio \(Oxyz\)
Rette perpendicolari nel piano \(Oxy\)
sono perpendicolari se e solo se
Due rette nel piano in coordinate cartesiane
sono perpendicolari
Retta perpendicolare ad un piano nello spazio \(Oxyz\)
Una retta
e un piano nello spazio in coordinate cartesiane
sono perpendicolari se e solo se
Retta perpendicolare ad un piano nello spazio \(Oxyz\)

Lezione 3
Posizioni reciproche tra rette nel piano \(Oxy\)
Due rette nel piano in coordinate cartesiane
Parallele non coincidenti
Incidenti
Rette coincidenti
- \(Rk(A)<Rk(A|c)\)
-
\(Rk(A)=Rk(A|c)=2\)
- \(Rk(A)=Rk(A|c)=1\)
Posizioni reciproche tra retta e piano nello spazio \(Oxyz\)
Una retta
e un piano nello spazio in coordinate cartesiane
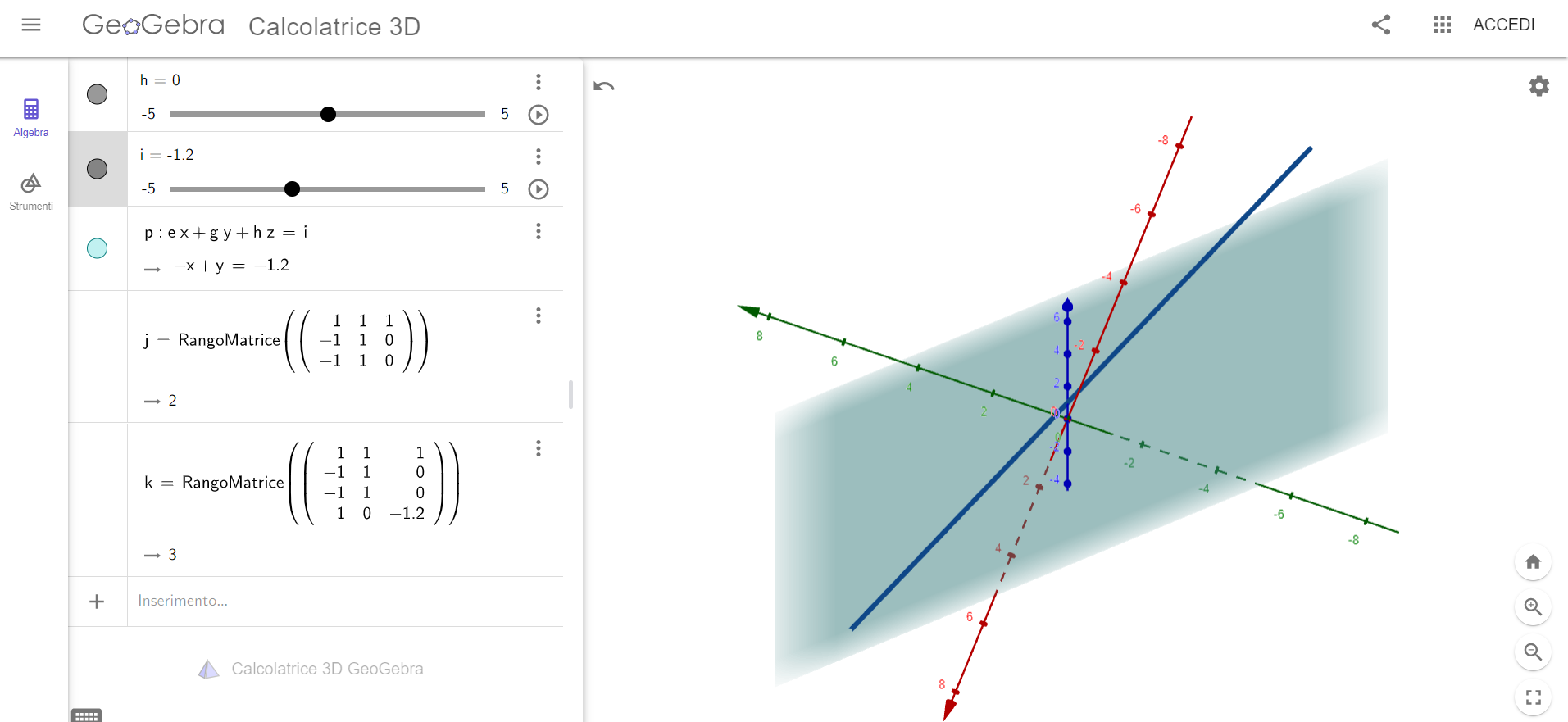
Paralleli con la retta esterna al piano
Incidenti
Retta giace sul piano
- \(Rk(A)<Rk(A|d)\)
-
\(Rk(A)=Rk(A|d)=3\)
- \(Rk(A)=Rk(A|d)=2\)
Posizioni reciproche tra retta e piano nello spazio \(Oxyz\)
Lezione 4
- Esercizi classici di calcolo dei punti di intersezione retta-piano nello spazio
- Prova laboratoriale con GeoGebra
N.B.: per i DSA discalculici solo prova 2.
Bibliografia
Libro di testo
Matematica blu Zanichelli 2.0 - Geometria nello spazio
GeoGebra
https://wiki.geogebra.org/it
Normative
- L. 107/2015 - Buona scuola
- L. 170/2010 - DSA
- D.P.R. 89/2010 - Regolamento licei