Zero-Noise Selection for Point Vortex Dynamics after Collapse
Milo Viviani (joint work with Francesco Grotto and Marco Romito)
Scuola Normale Superiore - Pisa
YoungStats Webinar - Stochastic fluid dynamics
15 November 2023
2D Euler Equations
Vorticity formulation
- \(\omega\) is the scalar vorticity field \(\omega=\nabla\times u\)
- \(\psi\) is the stream function
- The spatial domain is \(\mathbb{R}^2\)
- Global well posedness for \(\omega_0\in L^1(\mathbb{R}^2)\cap L^\infty(\mathbb{R}^2)\)
Point-vortex Equations
- \(x_i\) are the positions of the vortices
- \(\Gamma_i\) are the intensities of the vortices
- Well-posed for almost any initial configuration, w.r.t. the Lebesgue measure [Marchioro&Pulvirenti, 1994]
- The initial positions \(x_i(0)\) for which the vortices collapse is dense in \(\mathbb{R}^{2N}\), for \(N>2\)
for \(i=1,2,\dots,N\)
Point-vortex as solutions to the 2D Euler Equations
- Solves the Euler equations in the sense of distributions if the self-interaction terms are neglected [Schochet, 1996]
- Point-vortex equations can be obtained as limit of smooth solutions to the Euler equations
- Point-vortex solutions for a finite dimensional coadjoint orbit in \(\Xi_{vol}^*\) [Marsden&Weinstein, 1983]
Empirical measure
Continuation after collapse
Deterministic [Godota&Sakajo, 2016]
for \(i=1,2,\dots,N\)
where, for any \(\varepsilon>0\), \(K_\varepsilon = \varrho^\varepsilon\ast K\), \(K(x) = \frac{x^\perp}{|x|^2}\),
for \(\varrho:\mathbb{R}\rightarrow\mathbb{R}\) convolution kernel \(\varrho^\varepsilon(x) = \frac{1}{\varepsilon^2}\varrho(\frac{x}{\varepsilon})\)
Given \(x_1(0), x_2(0), x_3(0)\) collapsing intial configuration, for \(\varepsilon\rightarrow 0\)
- \(x_i^\varepsilon(t)\rightarrow x_i(t)\) for \(t\in[0,t_c]\)
- \(x_i^\varepsilon(t)\rightarrow \overline{x}_i(2t_c-t)\) for \(t\in[t_c,2t_c]\)
where \(\overline{x}_i=(x_{i,1},-x_{i,2})\)
Continuation after collapse
Stochastic [Flandoli&Gubinelli&Priola, 2011]
for \(i=1,2,\dots,N\)
where, for any \(\varepsilon>0\), \(B^i\) are i.i.d. 2D Brownian motions. Implies pathwise unique strong solution for \(t\geq 0\).
Given \(x_1(0)^\varepsilon, x_2(0)^\varepsilon, x_3(0)^\varepsilon\) collapsing intial configuration, for \(\varepsilon\rightarrow 0\)
- \(Law(x_1^\varepsilon,x_2^\varepsilon,x_3^\varepsilon)\Rightarrow Law(x_1,x_2,x_3)\), for \(\varepsilon\rightarrow 0\) in \(t\in[0,2t_c]\), up to subsequences
- Pathwise convergence before \(t_c\) but not after
OPEN QUESTION: What is the limit \(Law(x_1,x_2,x_3)\)?
First integrals in \(\mathbb{R}^2\)
The Point-vortex equations in \(\mathbb{R}^2\) admit the following first integrals
- Energy: \(H=-\frac{1}{2\pi}\sum_{i\neq j} \Gamma_i\Gamma_j \log|x_i-x_j|\)
- Barycenter: \(M=\sum_{i\neq j} \Gamma_ix_i\)
- Moment of intertia: \(I =\sum_{i\neq j} \Gamma_i\Gamma_j|x_i-x_j|^2\)
For N=3, the point-vortex equations exhibit (self similar) collapse in finite time if and only if
- \(\sum_{i\neq j} \Gamma_i\Gamma_j = 0\)
- \(I=\sum_{i\neq j} \Gamma_i\Gamma_j|x_i-x_j|^2 = 0\)
Reduced equations
-
For N=3, given a collapsing initial configuration with \(M=0\), by invariance under rotation and homotheties of the collapsing condition, we can study \(Rx_1\), such that
\(Rx_3=(1,0)\) and \(\Gamma_2Rx_2=-\Gamma_3Rx_3 -\Gamma_1Rx_1\), for a suitable matrix \(R\in O(2)^+\)
- Let \(Z:=Rx_1\)We then have \(H=H(Z)\) and \(I = I(Z)\)
- We study how \(H\) and \(I\) change after the collapse for \(\varepsilon\rightarrow 0\)
- The set \(\lbrace Z\in\mathbb{R}^2:H(Z)=H_0\cap I(Z)=I_0\rbrace\) determines the possible configurations
Numerical simulations
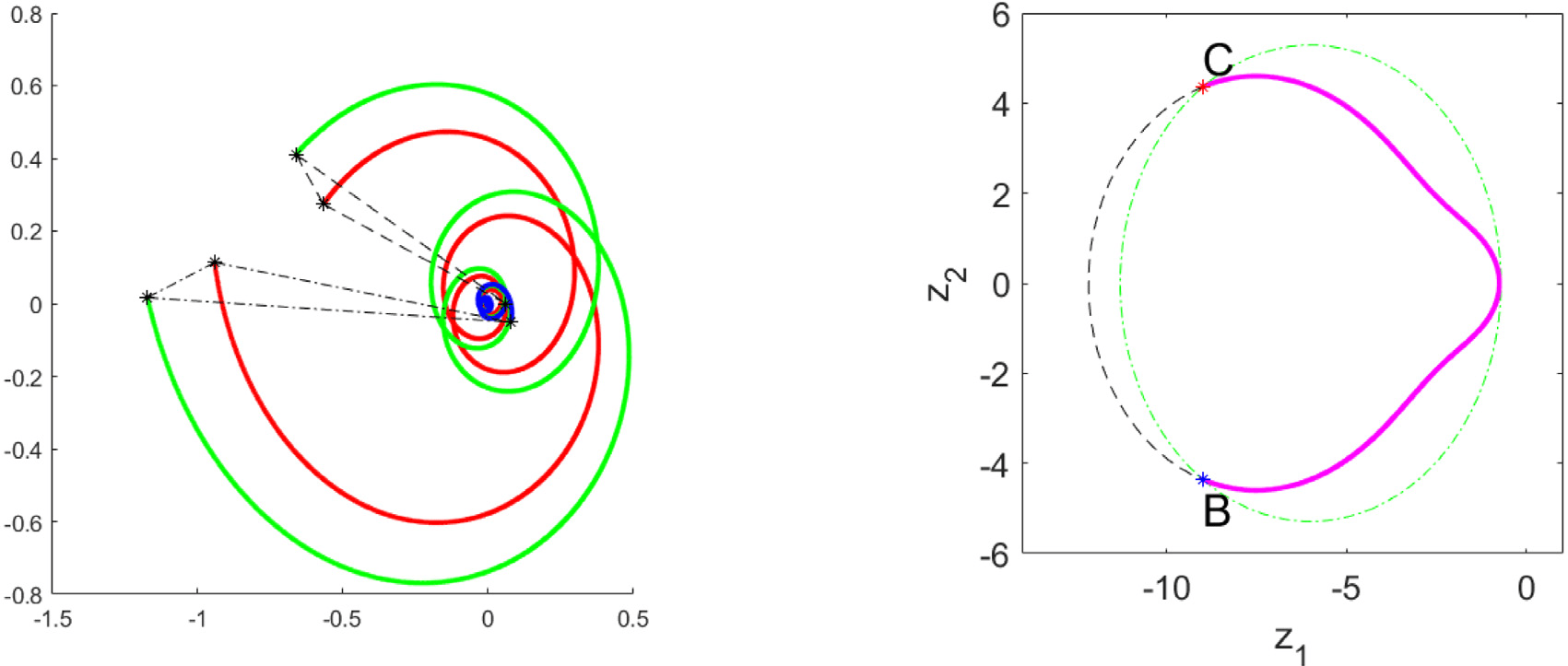
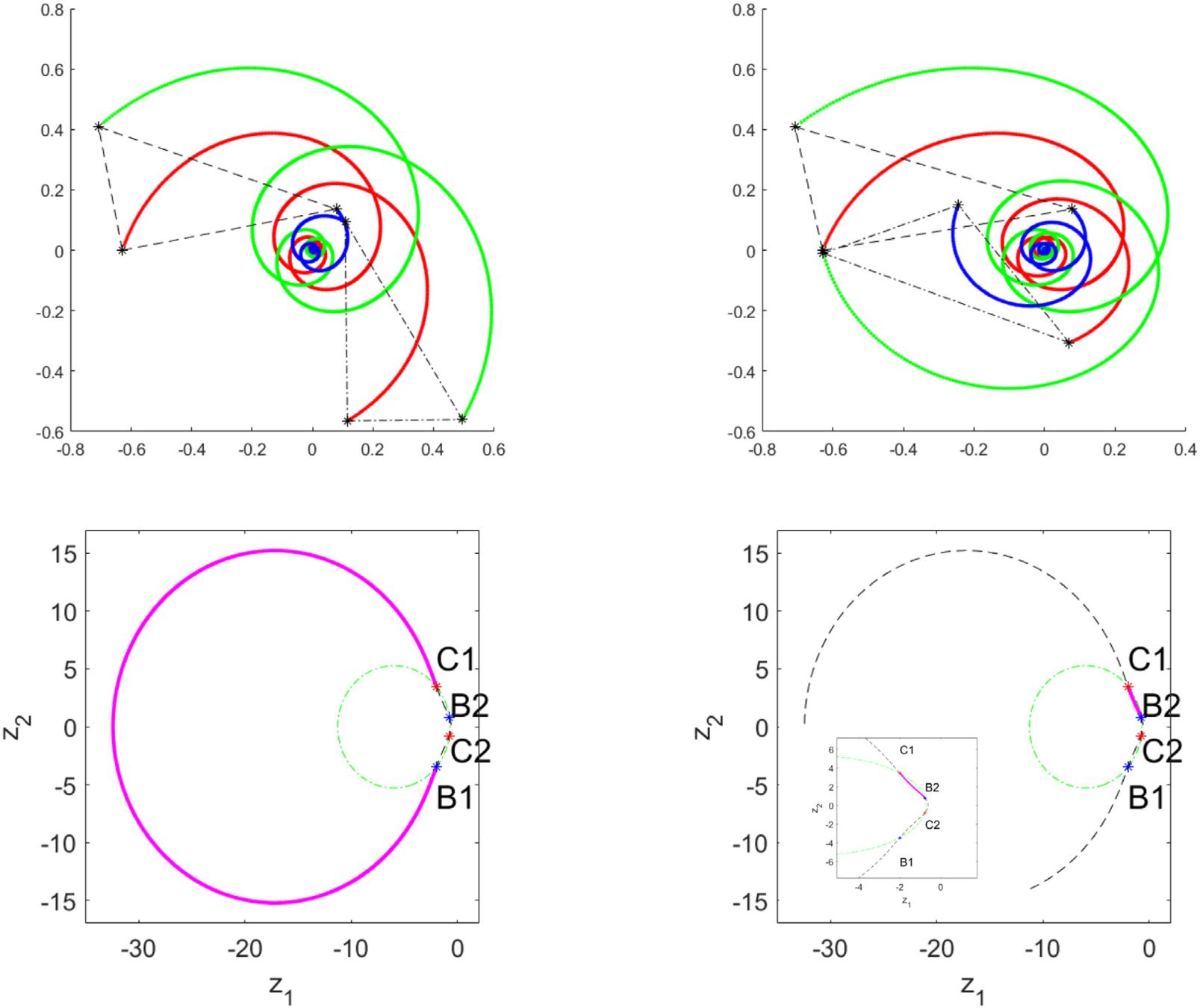
Trajectories \(x^\varepsilon_1,x^\varepsilon_2,x^\varepsilon_3\)
Evolution of \(Z(t)\) purple, green \(I=I_0\), black \(H=H_0\)
\(\varepsilon = 10^{-10}\)
Rmk: \(H\) and \(I\) are local martingales
Numerical scheme
- Adaptive symplectic integrator (midpoint scheme)
- Stochastic midpoint [Burrage&Burrage, 2014], two evaluations of the Wiener process
where the time-step \(h:=h(n)\) is such that \(h(n)\sigma(x^n_1,x^n_2,x^n_3)^\alpha=h(0)\sigma(x^0_1,x^0_2,x^0_3)^\alpha\), for \(\alpha=1.3\) and \( \sigma(x_1,x_2,x_3)=\frac{1}{\frac{1}{\|x_1-x_2\|^2}+\frac{1}{\|x_2-x_3\|^2}+\frac{1}{\|x_1-x_3\|^2}}\)
Statistics for the limiting distribution
- Evidences of non-uniform distribution of the reopening angle \(\theta\), defined as the angle between \(x_2^\varepsilon\) and the \(x-\)axis at \(t=2t_c\), for \(\varepsilon\rightarrow 0\):
- strong fluctuations of CDF for different \(\varepsilon\) may indicate non-unique limit distribution;
- p-values\(<<10^{-9}\), for \(\varepsilon=10^{-10}\), tested on the uniform distribution hypotesis for \(\theta\)
- Evidences of equal probability in keeping or changing configuration after collapse (4 intersections of \(H\) and \(I\)), p-value=0.295, for \(\varepsilon=10^{-10}\)
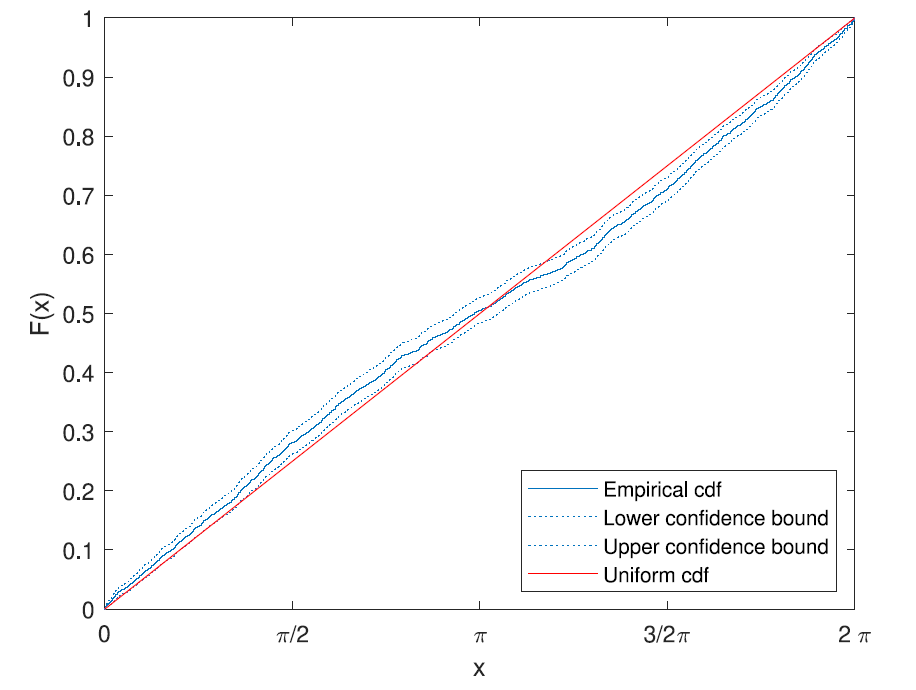
Empirical c.d.f. (solid blue) of the angle of \(x_2^\varepsilon(2t_c)\) for \(10^4\) samples, \(\varepsilon=10^{-10}\) . Dotted blue curves are confidence bounds (\(95\%\)) for the e.c.d.f. and the solid red line is the c.d.f. of the uniform distribution on \([0,2\pi]\).
Empirical CDF
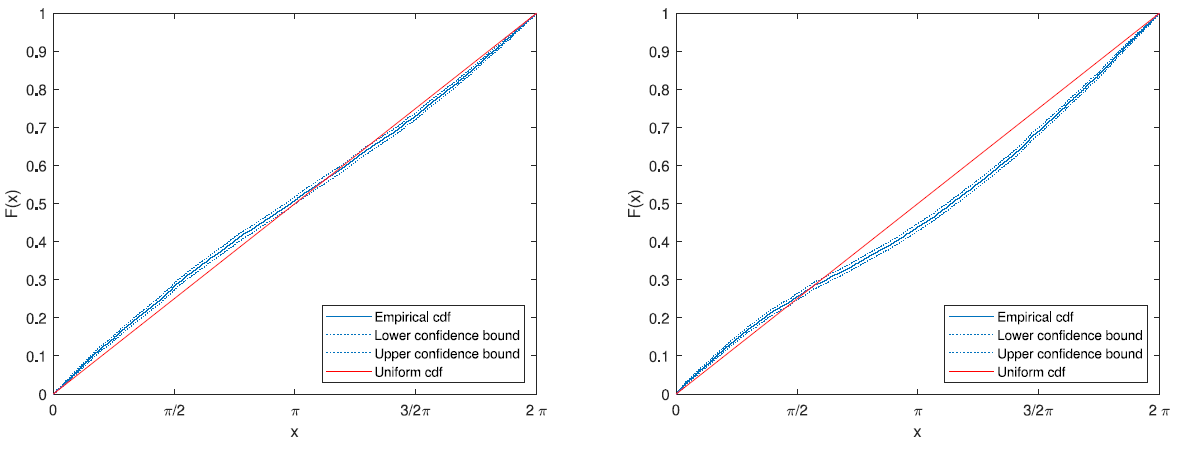
Empirical c.d.f. (solid blue) of the angle of \(x_2^\varepsilon(2t_c)\) for \(10^4\) samples, \(\varepsilon=10^{-10}\) . Dotted blue curves are confidence bounds (\(95\%\)) for the e.c.d.f. and the solid red line is the c.d.f. of the uniform distribution on \([0,2\pi]\). Samples being divided (right and left plots) according to the similarity class of the PV position triangle during burst.