Криптография без односторонних функций

Проект подготовили студенты группы 0372

Жуков Владимир
Пахаревская Элина

1/27

2/27

Данная работа выполнена с использованием материалов статьи "Secrecy without one-way functions" (D. Grigoriev, V. Shpilrain, 2013)

Роли членов команды

Пахаревская Элина:

- перевод статьи

- презентация

- анимации

Жуков Владимир:

- алгоритмы

- анимации

3/27

Содержание

Что такое односторонние функции?..................................................................5

Вычисление суммы чисел....................................................................................8

Вычисление произведения чисел....................................................................11

Сравнение двух чисел.........................................................................................13

Вычисление неоднородной функции..............................................................15

Битовая схема обязательств..............................................................................17

Ментальный покер..............................................................................................20

Решение квадратного уравнения.....................................................................24

Вычисление определителя матрицы...............................................................26

4/27

Что такое односторонние функции?

5/27

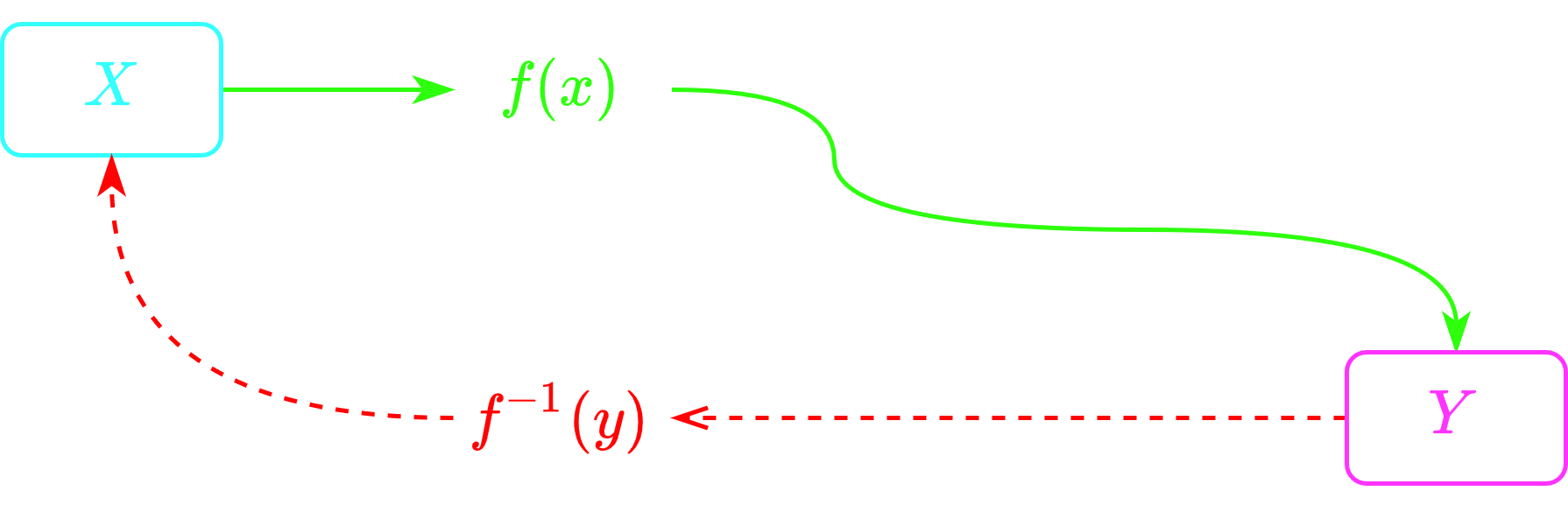
Односторонняя функция - это функция, которую довольно легко вычислить, но трудно* найти по значению функции соответствующее значение аргумента.

 

*Под «трудно найти» нужно понимать как: потребуется не один год расчетов с использованием ЭВМ.

Протоколы, представленные в проекте:

• вычисление суммы

• вычисление произведения

• сравнение двух чисел

• вычисление неоднородной функции

• битовая система обязательств

• ментальный покер

• решение квадратного уравнения

• вычисление определителя

6/27

7/27

Во всех описанных протоколах подразумевается следующее:

• ​все узлы объединены в замкнутую цепь \(P_1 \rightarrow P_2 \rightarrow \dots \rightarrow P_n\)
• передача информации между смежными узлами осуществляется по защищенным каналам (необходимо для предотвращения перехвата данных)
• все узлы в точности выполняют поставленные каждому из них в протоколе задачи
• для упрощения понимания протоколов рассматриваются примеры на множестве целых чисел

Вычисление суммы чисел

8/27

Постановка задачи: вычисление суммы элементов \(n_1,n_2, \dots,n_k\), хранимых узлами \(P_1, P_2, \dots,P_k\) соответственно, не раскрывая этих значений.

Протокол:

1. Узел \(P_1\) начинает алгоритм, отправляя случайное сгенерированное число \(n_{01}\) узлу \(P_2\).
2. Каждый узел \(P_i\) при получении элемента \(m\) от \(P_{i-1}\) прибавляет к нему свое число \(n_i\) и передает результат \(P_{i+1}\).
3. \(P_k\) также прибавляет к полученному от \(P_{k-1}\) свое число \(n_k\) и отправляет ее \(P_1\).
4. \(P_1\) прибавляет свое число \(n_1\) к полученному значению и вычитает из него \(n_{01}\). Теперь результат - это сумма \(S\) элементов всех узлов.
5. Узел \(P_1\) сообщает \(S\) остальным узлам по порядку, начиная со второго.\(^*\)

*После получения от \(P_k\) суммы \(S\) узел \(P_1\) может сравнивнить ее с той, которая была отправлена узлу \(P_2\). Если они отличаются, то в сети есть узел, который изменил сумму, то есть сообщил ложную информацию.

9/27

Исходный протокол:

1. Узел \(P_1\) начинает алгоритм, отправляя сумму \(n_1 + n_{01}\) узлу \(P_2\), где \(n_{01}\) - случайное число, сгенерированное \(P_1\).
2. Каждый узел от \(P_2\) до \(P_{k-1}\) включительно делают то же самое. \(P_i\) при получении элемента \(m\) от \(P_{i-1}\) прибавляет к нему свою сумму \(n_i+n_{0i}\) и передает результат \(P_{i+1}\).
3. \(P_k\) также прибавляет к полученному от \(P_{k-1}\) свою сумму \(n_k+n_{0k}\) и отправляет ее \(P_1\).
4. \(P_1\) вычитает \(n_{01}\) из полученного значения. Теперь результат - это сумма всех элементов и случайных чисел (кроме первого) узлов. После этого \(S\) становится известен всем.\(^*\)
5. Теперь все участники, кроме первого, раскрывают свои \(n_{0i}\) и происходит вычисление суммы этих значений. После этого вычисляется результат: из \(S\) вычитается сумма случайных чисел.
   
   *передаем по защищенному каналу, чтобы всем узлам не стало известно сгенерированное \(P_1\) число и \(P_2\) не смог вычислить хранимое \(P_1\) значение.

В исходном протоколе можно заметить избыточность. Если оставить способность генерации случайных чисел только первому узлу, не возникнет изменений ни в конечной сумме, ни в соблюдении секретности на всех шагах выполнения протокола. Мы предложили другой вариант, в котором сократится количество арифметических операций и снизится нагрузка на каналы связи.

10/27

Вычисление произведения чисел

11/27

Постановка задачи: вычисление произведения элементов \(n_1,n_2, \dots,n_k\), хранимых узлами \(P_1, P_2, \dots,P_k\) соответственно, не раскрывая этих значений.

Протокол для вычисления произведения также обладает избыточностью, что и протокол для вычисления суммы. Поэтому здесь также приведен измененный протокол.

12/27

Сравнение двух чисел

13/27

Постановка задачи: сравнить два числа \(n_1\) и \(n_2\), принадлежащие \(P_1\) и \(P_2\) соответственно, не раскрывая их значений.

Протокол:

1. \(P_1\) раскладывает свое число на разность \(n_1=n_{11}-n_{12}\). Затем отправляет \(n_{12}\) узлу \(P_2\).
2. \(P_2\) раскладывает свое число на разность \(n_2=n_{21}-n_{22}\). Затем отправляет \(n_{22}\) узлу \(P_1\).
3. \(P_1\) отправляет сумму \(n_{11}+n_{22}\) \(D\).
4. \(P_2\) отправляет сумму \(n_{21}+n_{12}\) \(D\).
5. \(D\) вычитает \(n_{21}+n_{12}\) из \(n_{11}+n_{22}\) чтобы получить \(n_1-n_2\) и выяснить результат.

На видео:

• Белые числа: \(n_i\)
• Нижние числа: \(n_{i1}\)
• Верхние числа: \(n_{i2}\)

14/27

Dummy - участник, которому запрещено генерировать случайные значения, он может лишь отвечать на конкретные запросы. В данном случае таким запросом будет вычисление суммы и возвращение результатов.

Вычисление неоднородной функции

15/27

Постановка задачи: поиск значения функции вида \(f(n_1,n_2,n_3)=n_1 \cdot n_2+g(n_3)\), где \(g\) - любая вычислимая функция.

Протокол:

1. Узел \(P_1\) начинает процесс с отправки случайного значения \(a_0\) узлу \(P_2\)
2. \(P_2\) умножает \(a_0\) на свое \(n_2\) и отправляет результат \(P_3\)
3. \(P_3\) умножает \(a_0 \cdot n_2\) на случайный элемент \(c_0\) и отправляет результат \(P_1\)
4. \(P_1\) умножает \(a_0 \cdot n_2 \cdot c_0\) на свой \(n_1\), делит его на \(a_0\) и отправляет результат обратно \(P_3\)
5. \(P_3\) делит \(n_1 \cdot n_2 \cdot c_0\) на \(c_0\), прибавляет \(g(n_3)\) и получает искомый результат \(n_1 \cdot n_2+g(n_3)\)

16/27

Битовая схема обязательств

17/27

Постановка задачи: организовать такой обмен значениями между узлами, при котором гарантируется

• секретность (к концу фазы передачи ни одна из сторон не владеет секретной информацией о другой стороне)
• однозначность (к концу фазы раскрытия отправленные и опубликованные узлами значения не должны отличаться).

Протокол:

1. Каждый узел раскладывает свое число на два случайных: \(n_i = r_i + s_i\). Если участники хотят работать с битами, то "0" они раскладывают или на \(0+0\) или на \(1+1\), а "1" на \(0+1\) или \(1+0\)
2. (Фаза передачи). \(P_1\) отправляет \(r_1\) узлу \(P_2\), затем \(P_2\) отправляет \(r_1+r_2\) узлу \(P_3\), \(P_3\) отправляет \(r_1+r_2+r_3\) узлу \(P_1\). После этого в обратную сторону, \(P_3\) отправляет \(s_3\) узлу \(P_2\), затем \(P_2\) отправляет \(s_2+s_3\) узлу \(P_1\), \(P_1\) отправляет \(s_1+s_2+s_3\) узлу \(P_3\).\(^*\)

*После этапа передачи ни один из участников не может восстановить какую-либо информацию о другом участнике. Имеющейся информации недостаточно. Можно исключить факт мошенничества, так как каждый фрагмент переданной узлу информации может быть подтвержден двумя другими.

18/27

После этапа передачи:

\(P_1\) знает: \(s_1\), \(r_1\), \(s_2 + s_3\), \(r_1+r_2+r_3\)

\(P_2\) знает: \(s_2\), \(r_2\), \(r_1\), \(s_3\)

\(P_3\) знает: \(s_3\), \(r_3\), \(r_1+r_2\), \(s_1+s_2+s_3\)

Частный случай. Частным случаем этой задачи является ситуация, когда участников двое. Для этого случая необходимо ввести третий узел Dummy, который не будет иметь возможности генерации случайных чисел и будет выступать в роли промежуточного.

3. (Фаза раскрытия) \(P_3\) отправляет \(n_1+n_2\) \(P_1\) и \(P_2\). Сейчас \(P_1\) знает \(n_2\), а \(P_2\) знает \(n_1\).
4. \(P_2\) отправляет \(r_1\) \(P_3\). Сейчас \(P_3\) может восстановить \(r_2\) с помощью \(r_1\) и \(r_1+r_2\).
5. \(P_1\) отправляет \(s_2+s_3\) \(P_3\). Сейчас \(P_3\) сможет узнать \(s_2\) из полученной суммы, зная \(r_2\), восстановить \(n_2\), а также \(n_1\) зная сумму \(n_1+n_2\).
6. \(P_1\) отправляет \(r_1+r_2+r_3\) \(P_2\). Теперь \(P_2\) может узнать \(r_3\) и восстановть \(n_3=r_3+s_3\)

19/27

Ментальный покер

20/27

Реализация: Идея алгоритма заключается в том, что сначала между участниками распределяются числа от 1 до \(m\) (количество карт), а после генерируется случайная перестановка из \(m\) элементов, используя которую карты раздаются игрокам.

Данный алгоритм реализуется путем последовательного выполнения двух протоколов, описания которых приведены на следующих слайдах.

Постановка задачи: необходимо раздать игрокам карты, гарантируя, что никто из них не сможет узнать карты другого или забрать себе заведомо выигрышную комбинацию.

21/27

Цель протокола 1: раздать числа каждому узлу так, чтобы никакой узел не мог догадаться о наборе чисел другого узла.

Протокол 1 (упрощенный):

1. \(P_1: m = 0 \rightarrow P_2\)
2. \(P_i:\) Если у узла меньше \(s = 6\) чисел, то:
   • Если узел встретил число впервые, то \(m \rightarrow P_{i + 1} \) и генерируется \(c_i \in [1; N]\)
   • Если \(q_m \le c_i\), то \(m \rightarrow P_{i + 1} \)
   • Если \(m = 36\), узел забирает его и передает следующему
   • Иначе узел забирает \(m \neq 0\) и \(m + 1 \rightarrow P_{i + 1}\)
3. Алгоритм завершается после того, как узел \(P_1\) видит число \(6s = 6 \cdot 6 = 36\) ровно N + 1 раз

Протокол 1:

Рассмотрим ситуацию, когда участников шестеро, а карт - 36 (\(s = \frac{36}{6} = 6\)). Перед началом все игроки договариваются о едином параметре \(N\), который означает максимальное количество обходов всех участников текущим числом. Пусть \(N=10\).

Формат данных узла:

\(q_m:c_i\), где \(q_m\) - счетчик получения узлом числа \(m\), \(c_i\) - максимальное значение счетчика \(q_m\)

22/27

Цель протокола 2: сгенерировать каждому участнику число, которое будет использовано в дальнейшем при непосредственной "раздаче карт"

Протокол 2:

Все узлы выбирают случайное число \(M\) от 1 до количества карт. Положим \(M\) = 36.

Протокол 2 (упрощенный):

1. \(P_{i - 1}: n_{i - 1} \mod M \rightarrow P_i \)
2. \(P_{i + 1}: n_{i + 1} \mod M \rightarrow P_i \)
3. \(P_i: n_i = (n_{i - 1} + n_{i + 1}) \mod M\)

Алгоритм раздачи карт:

1. Генерируется тождественная перестановка, количество элементов в которой равно числу карт в колоде
2. Выполняется тасование Кнута
3. Каждый узел получает карту, порядковый номер которой соответствует имеющемуся числу, полученного в первом протоколе

23/27

Решение квадратного уравнения

24/27

Постановка задачи: необходимо найти корни квадратного уравнения и сообщить их всем узлам \(P_1\), \(P_2\) и \(P_3\), которые хранят параметры соответственно \(a\), \(b\) и \(c\) в секретном виде.

Протокол (упрощенный):

1. \(P_1: n_1 = a \cdot m_1 \rightarrow P_3\)
2. \(P_3: n_2 = n_1 \cdot c \rightarrow P_2\)
3. \(P_1: m_1 \rightarrow P_2\)
4. \(P_2: \frac{n_2}{m_1} = a \cdot c \)
5. \(P_2: n_{01,02} = \left( -b \pm \sqrt{b^2 - 4ac} \over 2 \right) \cdot m_2 \rightarrow P_3\)
6. \(P_3: n_{11, 12} = n_{01, 02} \cdot m_3 \rightarrow P_1\)
7. \(P_1: n_{21, 22} = \frac{n_{11, 12}}{a} \rightarrow P_2\)
8. \(P_2: n_{31, 32} = \frac{n_{21, 22}}{m_2} \rightarrow P_3\)
9. \(P_3: x_{1, 2} = \frac{n_{31, 32}}{m_3} \rightarrow P_1, P_2\)

25/27

Положим \(m_1, m_2, m_3\) - случайные сгенерированные числа.

Вычисление определителя матрицы

26/27

Постановка задачи: необходимо найти определитель матрицы \(n\times n\), строки \(n_i\) которой распределены между \(n\) участниками сверху вниз.

Протокол:

1. Узел \(P_1\) умножает \(n_1\) на случайное сгенерированное число \(m_1\), и передает результат \(P_2\)
2. Узел \(P_i\) делает то же, объединяет полученное \(n_{i - 1}\) с \(n_i\) так, чтобы получилась матрица \(i \times n\), а \(n_i\) оказалась нижней строкой, и передает результат \(P_{i+1}\)
3. Последний узел передает \(P_1\) матрицу \(n \times n\), который находит ее определитель и посылает его \(P_2\)
4. \(P_i\) делит определитель на \(m_i\) и передает следующему узлу
5. Первый узел делит принятое число на \(m_1\), получая определитель исходной матрицы, который сообщает остальным участникам, начиная со второго

27/27

Замечание.

"Настоящая" секретность достигается на поле действительных чисел. На нем узлы не могут по НОД'у предположительно определить секретные случайные числа других узлов.