CS6015: Linear Algebra and Random Processes
Lecture 31: Describing distributions compactly, Bernoulli distribution, Binomial distribution
Learning Objectives
How can we describe distributions compactly ?
What is the Bernoulli distribution?
What is the Binomial distribution?
Discrete distributions
Probability Mass Functions for discrete random variables
Recap
Random variables

Distribution of a discrete random variable
An assignment of probabilities to all possible values that a discrete RV can take
(can be tedious even in simple cases)
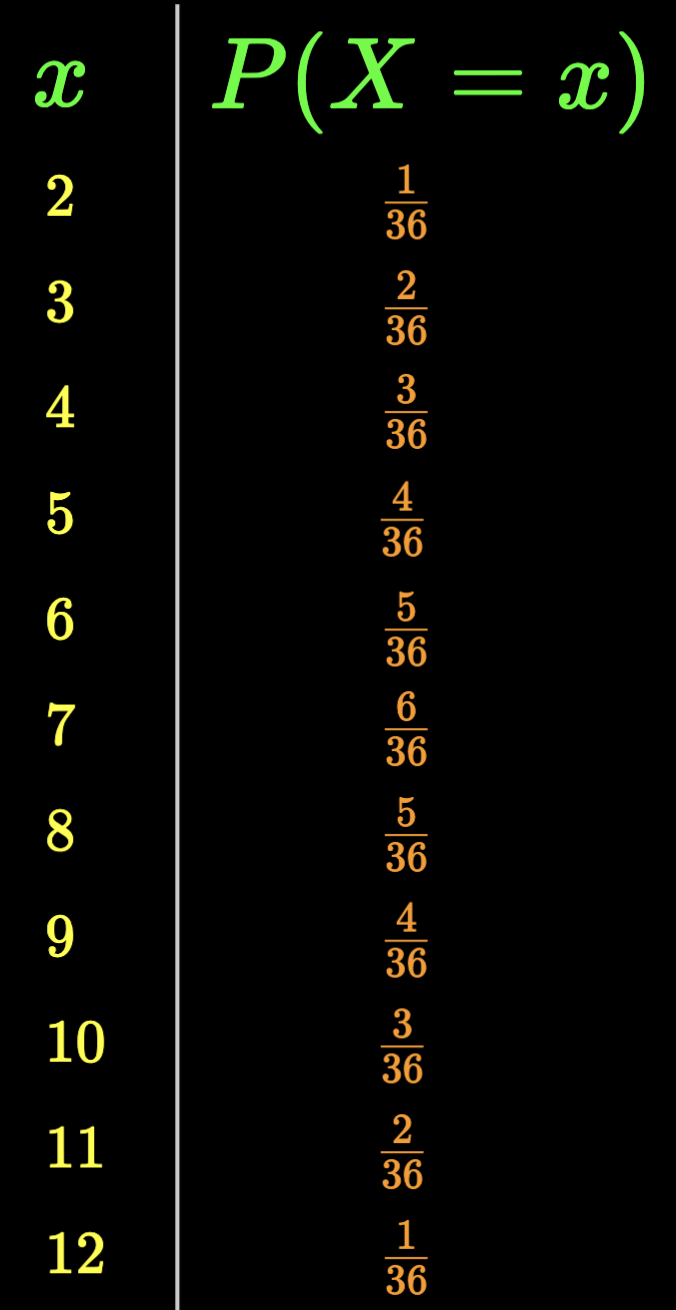
Can PMF be specified compactly?
p_X(x) = \begin{cases} \frac{1}{36} & if~x = 2 \\ \frac{2}{36} & if~x = 3 \\ \frac{3}{36} & if~x = 4 \\ \frac{4}{36} & if~x = 5 \\ \frac{5}{36} & if~x = 6 \\ \frac{6}{36} & if~x = 7 \\ \frac{5}{36} & if~x = 8 \\ \frac{4}{36} & if~x = 9 \\ \frac{3}{36} & if~x = 10 \\ \frac{2}{36} & if~x = 11 \\ \frac{1}{36} & if~x = 12 \\ \end{cases}
can be tedious to enumerate when the support of X is large
\mathbb{R}_X = \{1, 2, 3, 4, 5, 6, \dots, \infty\}
X: random variable indicating the number of tosses after which you observe the first heads
p_X(x) = \begin{cases} .. & if~x = 1 \\ .. & if~x = 2 \\ .. & if~x = 3 \\ .. & if~x = 4 \\ .. & if~x = 5 \\ .. & if~x = 6 \\ .. & .. \\ .. & .. \\ .. & if~x = \infty \\ \end{cases}
p_X(x) = (1-p)^{(x-1)}\cdot p
compact
easy to compute
no enumeration needed
but ... ....
Can PMF be specified compactly?
p: probability~of~heads
\mathbb{R}_X = \{1, 2, 3, 4, 5, 6, \dots, \infty\}
X: random variable indicating the number of tosses after which you observe the first heads
p_X(x) = (1-p)^{(x-1)}\cdot p
How did we arrive at the above formula?
Is it a valid PMF (satisfying propertied of a PMF)
What is the intuition behind it?
(we will return back to these Qs later)
Can PMF be specified compactly?
\mathbb{R}_X = \{1, 2, 3, 4, 5, 6, \dots, \infty\}
X: random variable indicating the number of tosses after which you observe the first heads
p_X(x) = (1-p)^{(x-1)}\cdot p
For now, the key point is
it is desirable to have the entire distribution be specified by one or few parameters
Can PMF be specified compactly?
Why is this important?
the entire distribution can be specified by some parameters

P(label = cat | image) ?
cat? dog? owl? lion?
p_X(x) = f(x)
A very complex function whose parameters are learnt from data!
Bernoulli Distribution

Experiments with only two outcomes

Outcome: {positive, negative}
Outcome: {pass, fail}

Outcome: {hit, flop}


Outcome: {spam, not spam}
Outcome: {approved, denied}
\{0, 1\}
X: \Omega
Bernoulli Random Variable
{failure, success}
\Omega:
Bernoulli trials
Bernoulli Distribution
\{0, 1\}
X: \Omega
Bernoulli Random Variable
{failure, success}
\Omega:
A:
event that the outcome is success
A:
Let~P(A) = P(success) = p
p_X(1) = p
p_X(0) = 1 - p
p_X(x) = p^x(1 - p)^{(1- x)}
Bernoulli Distribution
\{0, 1\}
X: \Omega
Bernoulli Random Variable
{failure, success}
\Omega:
p_X(x) \geq 0
\sum_{x \in\{0, 1\}}p_X(x) = p_X(0) + p_X(1)
= (1-p) + p = 1
\sum_{x \in\{0, 1\}}p_X(x) = 1 ?
Is Bernoulli distribution a valid distribution?
Binomial Distribution
Repeat a Bernoulli trial n times
independent
identical
(success/failure in one trial does not affect the outcome of other trials)
(probability of success 'p' in each trial is the same)




... n times
What is the probability of k successes in n trials?
(k \in [0, n])
Binomial Distribution (Examples)
Each ball bearing produced in a factory independently non-defective with probability p




... n times
If you select n ball bearings what is the probability that k of them will be defective?
Binomial Distribution (Examples)
The probability that a customer purchases something from your website is p




... n times
What is the probability that k out of the n customers will purchase something?
Assumption 1 : customers are identical (economic strata, interests, needs, etc)
Assumption 2 : customers are independent (one's decision does not influence another)
Binomial Distribution (Examples)
Marketing agency: The probability that a customer opens your email is p




... n times
If you send n emails what is the probability that the customer will open at least one of them?
Binomial Distribution




... n times
p_X(x) = ?
X:
random variable indicating the the number of successes in n trials
x \in \{0, 1, 2, 3, \dots, n\}
Challenge:
n and k can be very large
difficlult to enumerate all probabilities
Binomial Distribution




... n times
p_X(x) = ?
X:
random variable indicating the the number of successes in n trials
x \in \{0, 1, 2, 3, \dots, n\}
Desired:
Fully specify in terms of n and p
p_X(x)
(we will see how to do this)
Binomial Distribution




... n times
S, F
How many different outcomes can we have if we repeat a Bernoulli trial n times?
(sequence of length n from a given set of 2 objects)
2^n~outcomes
Binomial Distribution




... n times
TTT\\
TTH\\
THT\\
THH\\
HTT\\
HTH\\
HHT\\
HHH
Example: n = 3, k = 1
\Omega
0\\
1\\
2\\
3\\
X
A = \{HTT, THT, TTH\}
p_X(1) = P(A)
P(A) = P(\{HTT\}) \\+ P(\{THT\}) \\+P(\{TTH\})
P(\{HTT\}) = p(1-p)(1-p)
P(\{THT\}) = (1-p)p(1-p)
P(\{TTH\}) = (1-p)(1-p)p
Binomial Distribution




... n times
Example: n = 3, k = 1
A = \{HTT, THT, TTH\}
= 3 (1-p)^{(3-1)}p^1
p_X(1) = P(A) = 3 (1-p)^2p
= {3 \choose 1} (1-p)^{(3-1)}p^1
Binomial Distribution




... n times
Example: n = 3, k = 2
B = \{HTH, HHT, THH\}
= 3 (1-p)^{(3-2)}p^2
p_X(2) = P(B) = 3 (1-p)p^2
= {3 \choose 2} (1-p)^{(3-2)}p^2
Binomial Distribution




... n times
Observations
n \choose k
favorable outcomes
each of the k successes occur independently with a probability p
each of the n-k failures occur independently with a probability 1 - p
terms in the summation
n \choose k
each term will have the factor
p^k
each term will have the factor
(1-p)^{(n-k)}
n \choose k
p^k
(1-p)^{(n-k)}
Binomial Distribution




... n times
terms in the summation
n \choose k
each term will have the factor
p^k
each term will have the factor
(1-p)^{(n-k)}
n \choose k
p^k
(1-p)^{(n-k)}
p_X(k) =
Parameters:
p, n
the entire distribution is full specified once the values of p and n are known
Example 1: Social distancing




... n times
Suppose 10% of your colleagues from workplace are infected with COVID-19 but are asymptomatic (hence come to office as usual)
Suppose you come in close proximity of 50 of your colleagues. What is the probability of you getting infected?
(Assume you will get infected if you come in close proximity of a person)
Trial: Come in close proximity of a person
p = 0.1 - probability of success/infection in a single trial
n = 50 trials
Example 1: Social distancing




... n times
Suppose 10% of your colleagues from workplace are infected with COVID-19 but are asymptomatic (hence come to office as usual)
Suppose you come in close proximity of 50 of your colleagues. What is the probability of you getting infected?
n = 50, p = 0.1
P(getting~infected) = P(at~least~one~success)
= 1 - P(0~successes)
= 1 - p_X(0)
= 1 - {50 \choose 0}p^0(1-p)^{50}
= 1 - 1*1*0.9^{50} = 0.9948
Stay at home!!
Example 1: Social distancing




... n times
Suppose 10% of your colleagues from workplace are infected with COVID-19 but are asymptomatic (hence come to office as usual)
What if you interact with only 10 colleagues instead of 50
n = 10, p = 0.1
P(getting~infected) = P(at~least~one~success)
= 1 - P(0~successes)
= 1 - p_X(0)
= 1 - {10 \choose 0}p^0(1-p)^{10}
= 1 - 1*1*0.9^{10} = 0.6513
Still stay at home!!
Example 1: Social distancing




... n times
Suppose 10% of your colleagues from workplace are infected with COVID-19 but are asymptomatic (hence come to office as usual)
What if only 2% of your colleagues are infected instead of 10% ?
n = 10, p = 0.02
P(getting~infected) = P(at~least~one~success)
= 1 - P(0~successes)
= 1 - p_X(0)
= 1 - {10 \choose 0}p^0(1-p)^{10}
= 1 - 1*1*0.98^{10} = 0.1829
Perhaps, still not worth taking a chance!!
Example 2: Linux users




... n times
10% of students in your class use linux. If you select 25 students at random
(a) What is the probability that exactly 3 of them are using linux
(b) What is the probability that between 2 to 6 of them are using linux ?
(c) How would the above probabilities change if instead of 10%, 90% were using linux ?
n = 25, p =0.1, k = 3
n = 25, p =0.1, k = {2,3,4,5,6}
n = 25, p =0.9, p = 0.5
Example 2: Linux users




... n times
10% of students in your class use linux. If you select 25 students at random
n = 25, p =0.1, k = 3
n = 25, p =0.1, k = {2,3,4,5,6}
n = 25, p =0.9, p = 0.5
import seaborn as sb
import numpy as np
from scipy.stats import binom
x = np.arange(0, 25)
n=25
p = 0.1
dist = binom(n, p)
ax = sb.barplot(x=x, y=dist.pmf(x))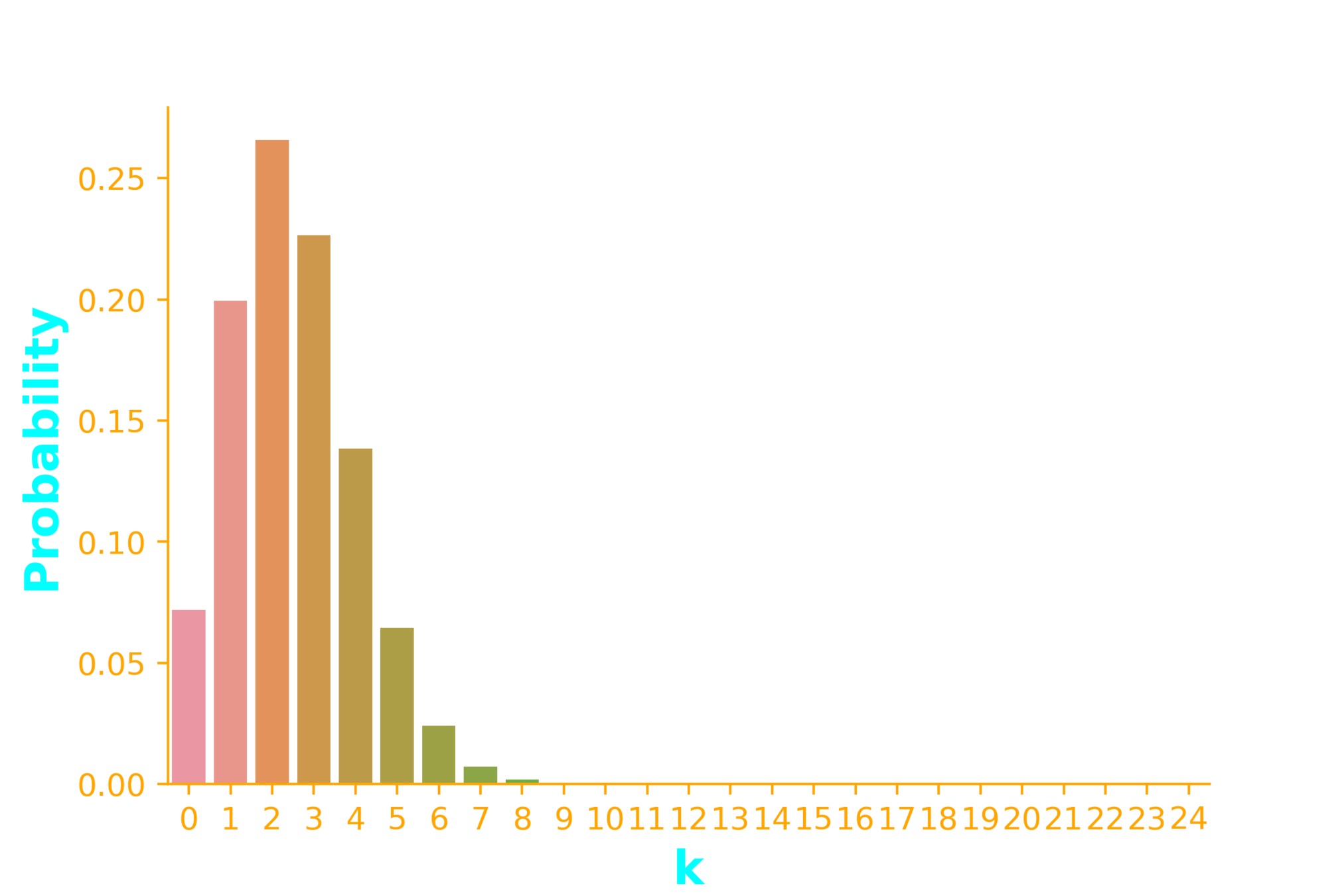
n \choose k
p^k
(1-p)^{(n-k)}
p_X(k) =
2042975 * 0.1^9 *0.9^{16}
= 0.000378
Example 2: Linux users




... n times
10% of students in your class use linux. If you select 25 students at random
n = 25, p =0.1, k = 3
n = 25, p =0.1, k = {2,3,4,5,6}
n = 25, p =0.9, p = 0.5
import seaborn as sb
import numpy as np
from scipy.stats import binom
x = np.arange(0, 25)
n=25
p = 0.1
dist = binom(n, p)
ax = sb.barplot(x=x, y=dist.pmf(x))n \choose k
p^k
(1-p)^{(n-k)}
p_X(k) =
2042975 * 0.1^{16} *0.9^{9}
= 7.1*10^{-11}
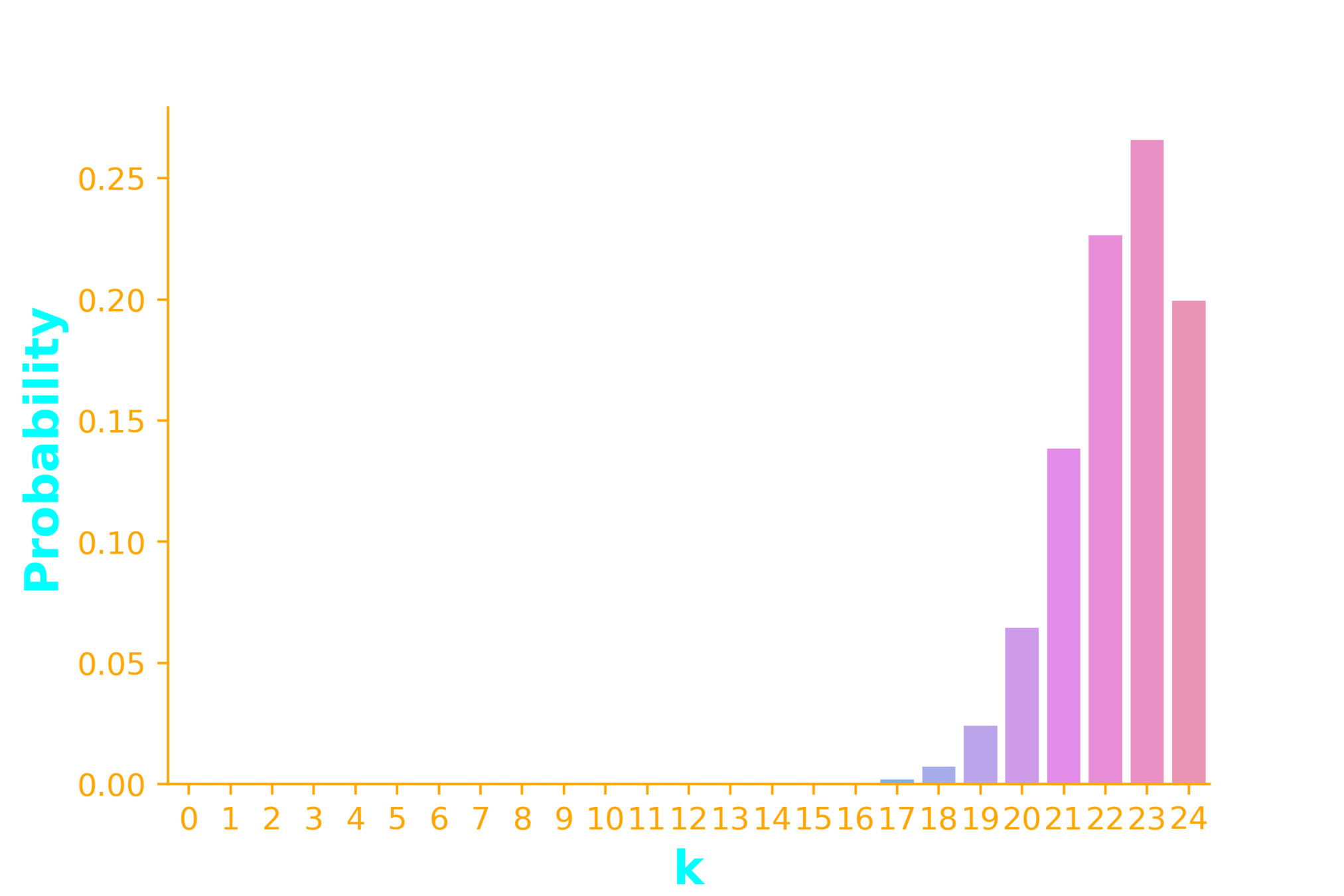
Example 2: Linux users




... n times
10% of students in your class use linux. If you select 25 students at random
n = 25, p =0.1, k = 3
n = 25, p =0.1, k = {2,3,4,5,6}
n = 25, p =0.9, p = 0.5
import seaborn as sb
import numpy as np
from scipy.stats import binom
x = np.arange(0, 25)
n=25
p = 0.1
dist = binom(n, p)
ax = sb.barplot(x=x, y=dist.pmf(x))n \choose k
p^k
(1-p)^{(n-k)}
p_X(k) =
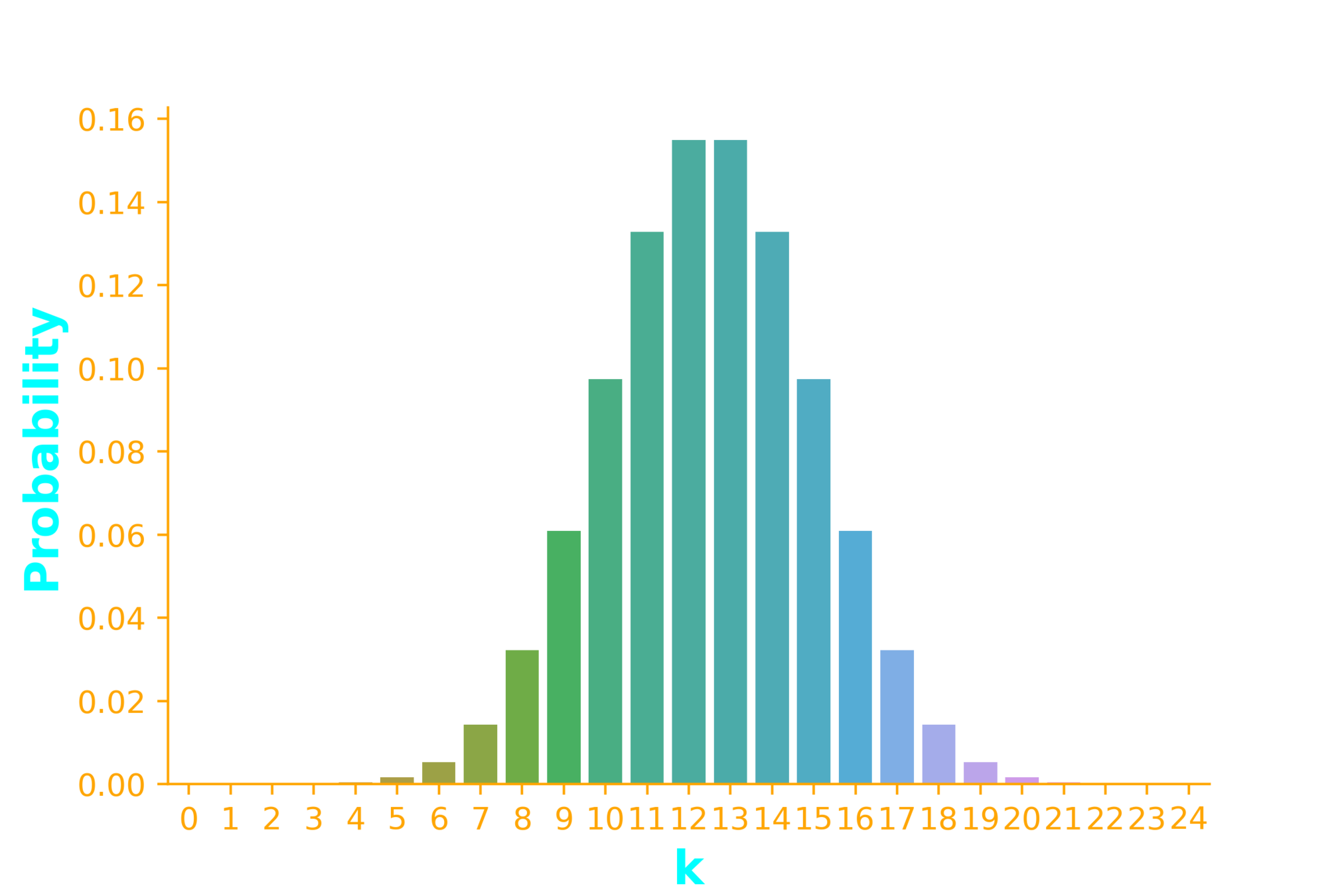
Binomial Distribution
p_X(x) \geq 0
\sum_{i=0}^n p_X(i) = 1 ?
Is Binomial distribution a valid distribution?




... n times
n \choose k
p^k
(1-p)^{(n-k)}
p_X(k) =
Binomial Distribution
\sum_{i=0}^n p_X(i) = 1 ?




... n times
\sum_{i=0}^n p_X(i)
= p_X(0) + p_X(1) + p_X(2) + \cdots + p_X(n)
= {n \choose 0} p^0(1-p)^{n} + {n \choose 1} p^1(1-p)^{(n - 1)} + {n \choose 2} p^2(1-p)^{(n - 2)} + \dots {n \choose n} p^n(1-p)^{0}
(a+b)^n = {n \choose 0} a^0b^{n} + {n \choose 1} a^1b^{(n - 1)} + {n \choose 2} a^2b^{(n - 2)} + \dots {n \choose n} a^n(b)^{0}
a = p, b = 1- p
Bernoulli (a special case of Binomial)




... n times
n \choose k
p^k
(1-p)^{(n-k)}
p_X(k) =
Binomial
Bernoulli
n = 1, k \in \{0, 1\}
p_X(0) = {1 \choose 0} p^0 (1-p)^1 = 1 - p
p_X(1) = {1 \choose 1} p^1 (1-p)^0 = p