CS6015: Linear Algebra and Random Processes
Lecture 34: Joint distribution, conditional distribution and marginal distribution of multiple random variables
Learning Objectives
What are joint, conditional and marginal pmfs?
What is conditional expectation?
What is the expectation of a function of multiple random variables?
Multiple random variables
X_1
X_2
X_3
X_4
X_5
Salinity
Pressure
Temperature
Y
Depth
Density
Oil
0/1
0/1
0/1
0/1
0/1
0/1
0: High 1: Low
Multiple random variables
Questions of Interest
P(Y=0|X_1=x_1, X_2=x_2, X_3=x_3, X_4=x_4, X_5=x_5, X_6=x_6)
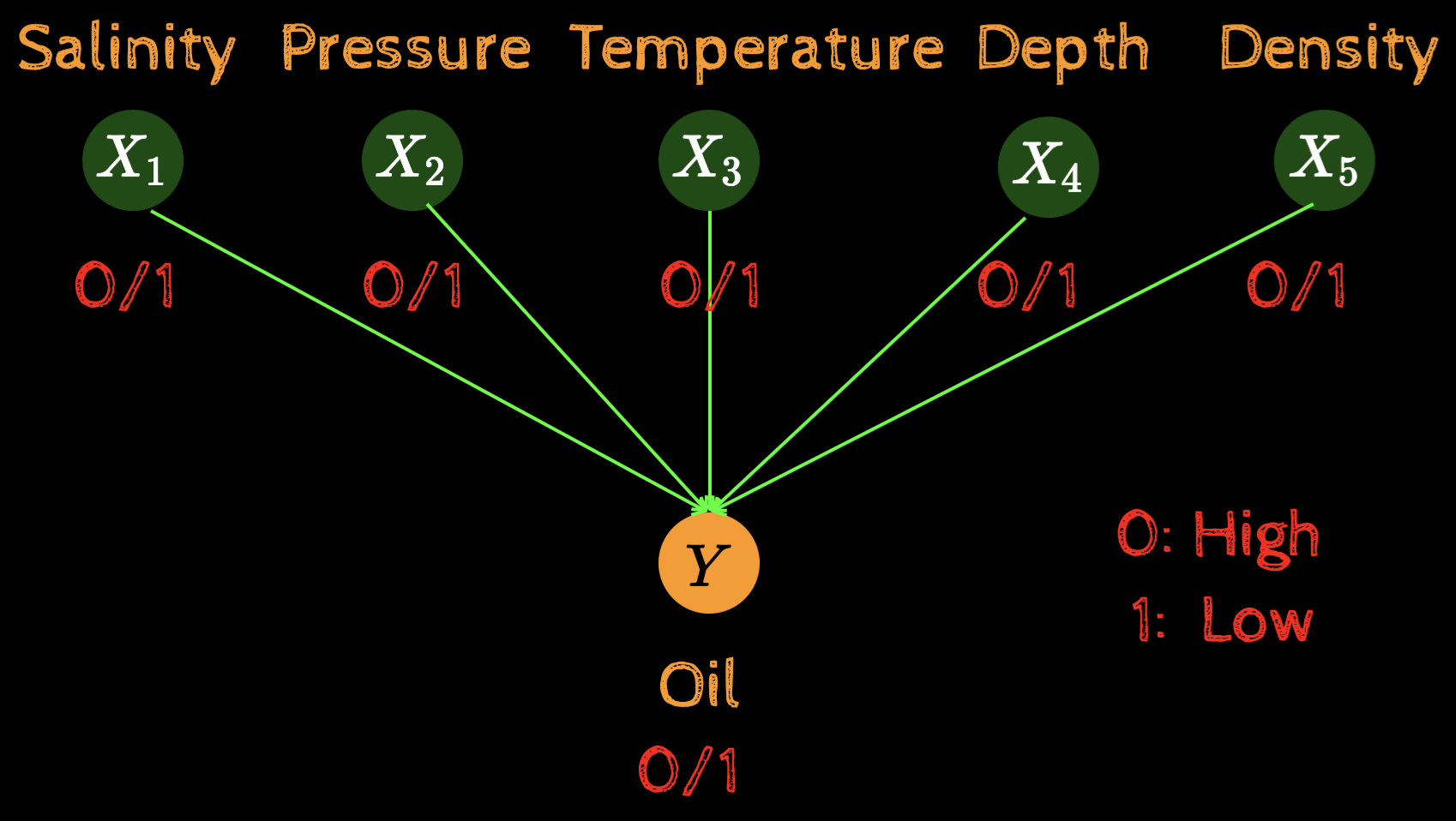
What is the probability that we will find oil?
What is the probability that everything will be high?
P(X_1=1,X_2=1,X_3=1,X_4=1,X_5=1,Y=1)
joint probability
conditional probability
P(X_5=1)
What is the probability that density will be high?
marginal probability
Understanding the notation
P(Y=0|X_1=x_1, X_2=x_2, X_3=x_3, X_4=x_4, X_5=x_5, X_6=x_6)
We have already discussed conditional distribution of events
The "event" notation
The "random variable" notation
P(\overbrace{Y=0}|\overbrace{X_1=x_1}, \overbrace{X_2=x_2}, \overbrace{X_3=x_3}, \overbrace{X_4=x_4}, \overbrace{X_5=x_5}, \overbrace{X_6=x_6})
events
p_{Y|X_1,X_2,X_3,X_4,X_5}(y|x_1,x_2,x_3,x_4,x_5)
\underbrace{~~~~~~~~~~~~~~~~~~~~~~~~~~~}
given
i.e., the values of these random variables are fixed
random variables
This is not a new concept - just a change of notation
Understanding the notation
p_X(x) = P(X=x)
p_{X,Y}(x,y) = P(X=x, Y=y)
p_{X|Y}(x|y) = P(X=x| Y=y)
marginal
conditional
joint
We will soon see that if we know the joint pmf we can compute the marginal and the conditional
Understanding the notation
P(X_1=x_1, X_2=x_2, X_3=x_3, X_4=x_4, X_5=x_5, X_6=x_6,Y=0)
p_{X_1,X_2,X_3,X_4,X_5,Y}(x_1,x_2,x_3,x_4,x_5,y)
P(Y=0|X_1=x_1, X_2=x_2, X_3=x_3, X_4=x_4, X_5=x_5, X_6=x_6)
joint probability of multiple events
joint pmf: 2^n different inputs possible
conditional probability
P(Y=0)
probability of a single event
p_{Y|X_1,X_2,X_3,X_4,X_5}(y|x_1,x_2,x_3,x_4,x_5)
conditional pmf: function of y, other values fixed
p_{Y}(y)
marginal pmf
Example
X: number of heads
| -1 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 1/8 | 0 | 0 | 0 |
| 1 | 0 | 1/8 | 1/8 | 1/8 |
| 2 | 0 | 2/8 | 1/8 | 0 |
| 3 | 0 | 1/8 | 0 | 0 |
TTT\\
TTH\\
THT\\
THH\\
HTT\\
HTH\\
HHT\\
HHH
\Omega
-1\\
3\\
2\\
2\\
1\\
1\\
1\\
1
0\\
1\\
1\\
2\\
1\\
2\\
2\\
3
X
Y
Y: position of first heads (-1 if no heads)
Y\\\overbrace{~~~~~~~~~~~~~~~~~~~~~~~}
X\begin{cases}
~\\
~\\
~\\
\end{cases}
p_{X,Y}(x,y)
=P(X=x, Y=y)
Can we compute the conditional and marginal distributions from the joint pmf?
Example
| -1 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 1/8 | 0 | 0 | 0 |
| 1 | 0 | 1/8 | 1/8 | 1/8 |
| 2 | 0 | 2/8 | 1/8 | 0 |
| 3 | 0 | 1/8 | 0 | 0 |
TTT\\
TTH\\
THT\\
THH\\
HTT\\
HTH\\
HHT\\
HHH
\Omega
-1\\
3\\
2\\
2\\
1\\
1\\
1\\
1
0\\
1\\
1\\
2\\
1\\
2\\
2\\
3
X
Y
Y\\\overbrace{~~~~~~~~~~~~~~~~~~~~~~~}
X\begin{cases}
~\\
~\\
~\\
\end{cases}
p_{X,Y}(x,y)
=P(X=x, Y=y)
Can we compute the conditional and marginal distributions from the joint pmf?
p_{X}(x) = \sum_{y}p_{X,Y}(x,y)
summing over all the different ways in which \(X\) can take the value \(x\)
Example
| -1 | 1 | 2 | 3 | |
|---|---|---|---|---|
| 0 | 1/8 | 0 | 0 | 0 |
| 1 | 0 | 1/8 | 1/8 | 1/8 |
| 2 | 0 | 2/8 | 1/8 | 0 |
| 3 | 0 | 1/8 | 0 | 0 |
TTT\\
TTH\\
THT\\
THH\\
HTT\\
HTH\\
HHT\\
HHH
\Omega
-1\\
3\\
2\\
2\\
1\\
1\\
1\\
1
0\\
1\\
1\\
2\\
1\\
2\\
2\\
3
X
Y
Y\\\overbrace{~~~~~~~~~~~~~~~~~~~~~~~}
X\begin{cases}
~\\
~\\
~\\
\end{cases}
p_{X,Y}(x,y)
=P(X=x, Y=y)
Can we compute the conditional and marginal distributions from the joint pmf?
p_{X|Y}(x|y) = P(X=x|Y=y)
= \frac{P(X=x,~Y=y)}{P(Y=y)}
= \frac{p_{X,Y}(x,y)}{p_{Y}(y)}
= \frac{p_{X,Y}(x,y)}{\sum_x p_{X,Y}(x,y)}
Revisiting the laws
Multiplication/Chain Rule
p_{X,Y}(x,y)
=p_{X|Y}(x|y) p_Y(y)
P(X=x, Y=y) = P(X=y|Y=y)P(Y=y)
Total Probability Theorem
p_{X}(x)
=\sum_{y} p_{X|Y}(x|y) p_Y(y)
P(X=x) = \sum_i P(X=x|Y=y_i)P(Y=y_i)
= \sum_{y}p_{X,Y}(x,y)
Bayes' Theorem
p_{X|Y}(x|y)
= \frac{p_{X,Y}(x,y)}{p_Y(y)}
= \frac{p_{X,Y}(x,y)}{\sum_x p_{X,Y}(x,y)}
= \frac{p_{Y|X}(y|x) p_X(x)}{\sum_x p_{Y|X}(y|x) p_X(x)}
A_1
A_5
A_4
A_3
A_2
A_6
A_7
B
\Omega
Revisiting the laws
Bayes' Theorem
\overbrace{p_{X|Y}(x|y)}
= \frac{\overbrace{p_{Y|X}(y|x)} \overbrace{p_X(x)}}{\sum_x p_{Y|X}(y|x) p_X(x)}
Prior
Likelihood
Posterior
Revisiting the laws
\sum_{x}\sum_{y}p_{X,Y}(x,y) = 1
\sum_{x}p_{X}(x) = 1
\sum_{x}p_{X|Y}(x|y) = 1
\sum_{y}p_{X|Y}(x|y) \neq 1
Generalising to more variables
p_{X,Y,Z}(x,y,z)
=p_X(x) p_{Y|X}(y|x) p_{Z|X,Y}(z|x,y)
| 0 | 0 | 1/4 | 3/4 |
| 0 | 1 | 1/8 | 7/8 |
| 1 | 0 | 2/5 | 3/5 |
| 1 | 1 | 1/2 | 1/2 |
p_{Z|X,Y}(z|x,y)
Z
X
Y
p_Z(z) = \sum_x\sum_y p_{X,Y,Z}(x,y,z)
Conditional distribution
Z=0
Z=1
Joint distribution
Marginal distribution
| 0 | 0 | 0 | 1/21 |
| 0 | 0 | 1 | 3/21 |
| 0 | 1 | 0 | 1/21 |
| 0 | 1 | 1 | 7/21 |
| 1 | 0 | 0 | 2/21 |
| 1 | 0 | 1 | 3/21 |
| 1 | 1 | 0 | 2/21 |
| 1 | 1 | 1 | 2/21 |
X
Y
p_{X,Y,Z}
| 0 | 6/21 |
| 1 | 15/21 |
Z
p_Z(z)
Independence
p_{X,Y,Z}(x,y,z)
=p_X(x) p_{Y|X}(y|x) p_{Z|X,Y}(z|x,y)
\(X,Y,Z\) are independent if
p_{X,Y,Z}(x,y,z)
=p_X(x) p_{Y}(y) p_{Z}(z)
\forall x,y,z
Z
| 0 | 0 | 0 | 1/20 |
| 0 | 0 | 1 | 3/20 |
| 0 | 1 | 0 | 2/20 |
| 0 | 1 | 1 | 6/20 |
| 1 | 0 | 0 | 1/20 |
| 1 | 0 | 1 | 3/20 |
| 1 | 1 | 0 | 1/20 |
| 1 | 1 | 1 | 3/20 |
X
Y
p_{X,Y,Z}
| 0 | 5/20 |
| 1 | 15/20 |
Z
p_Z(z)
| 0 | 0 | 1/4 | 3/4 |
| 0 | 1 | 1/4 | 3/4 |
| 1 | 0 | 1/4 | 3/4 |
| 1 | 1 | 1/4 | 3/4 |
p_{Z|X,Y}(z|x,y)
X
Y
Z=0
Z=1
| 1/4 |
|---|
| 3/4 |
| 1/20 |
|---|
| 3/20 |
| 2/20 |
| 6/20 |
| 2/20 |
| 2/20 |
| 0/20 |
| 4/20 |
| 0 | 0 | 1/4 | 3/4 |
| 0 | 1 | 1/4 | 3/4 |
| 1 | 0 | 1/2 | 1/2 |
| 1 | 1 | 0 | 1 |
X
Y
Z=0
Z=1
p_{Z|X,Y}(z|x,y)








Independence
\(X_1,X_2,X_3, \dots, X_n\) are independent if
p_{X_1,X_2,X_3, \dots, X_n}(x_1,x_2,x_3, \dots, x_n)
=p_{X1}(x_1) p_{X2}(x_2) p_{X3}(x_3)\dots p_{Xn}(x_n)
\forall x_1,x_2,x_3, \dots, x_n
Expectation: Recap
E[X] = \sum_x xp_X(x)
If we interpret \(p_X(x)\) as the long term relative frequency then \(E[X]\) is the long term average value of \(X\)
E[g(X)] = \sum_x g(x)p_X(x)
What if we have a function of multiple random variables?
Conditional Expectation
E[X|A]
What is the expected value of the sum of two die given that the second die shows an even number
X:
random variable indicating sum of the dice
A:
event that the second die shows an even no.
What are we interested in?
E[X] = \sum_x xp_X(x)
= \sum_x xp_{X|A}(x)
| (1 , 1) | (1 , 2) | (1 , 3) | (1 , 4) | (1 , 5) | (1 , 6) |
|---|---|---|---|---|---|
| (2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) | (2, 6) |
| (3, 1) | (3, 2) | (3, 3) | (3, 4) | (3, 5) | (3, 6) |
| (4, 1) | (4, 2) | (4, 3) | (4, 4) | (4, 5) | (4, 6) |
| (5, 1) | (5, 2) | (5, 3) | (5, 4) | (5, 5) | (5, 6) |
| (6, 1) | (6, 2) | (6, 3) | (6, 4) | (6, 5) | (6, 6) |
| (1 , 2) | (1 , 4) | (1 , 6) |
|---|---|---|
| (2, 2) | (2, 4) | (2, 6) |
| (3, 2) | (3, 4) | (3, 6) |
| (4, 2) | (4, 4) | (4, 6) |
| (5, 2) | (5, 4) | (5, 6) |
| (6, 2) | (6, 4) | (6, 6) |
A
\Omega
\mathbb{R}_X ={3,4,5,6,7,8,9,10,11,12}
p_{X|A} ={\frac{1}{18},\frac{1}{18},\frac{2}{18},\frac{2}{18},\frac{3}{18},\frac{3}{18},\frac{2}{18},\frac{2}{18},\frac{1}{18},\frac{1}{18}}
= 7.5
Conditional Expectation
E[g(X)|A]
E[X] = \sum_x xp_X(x)
= \sum_x g(x)p_{X|A}(x)
E[X|A]
= \sum_x xp_{X|A}(x)
Instead of conditioning on events we can condition on random variables
E[X|Y=y]
= \sum_x xp_{X|Y}(x|y)
E[g(X)|Y=y]
= \sum_x g(x)p_{X|Y}(x|y)
Total Expectation Theorem
E[X] = \sum_x xp_X(x)
A_1
A_5
A_4
A_3
A_2
A_6
A_7
B
\Omega
p_{X}(x) = \sum_{i=1}^n P(A_i)p_{X|A_i}(x)
Multiply by \(x\) on both sides and sum over \(x\)
\sum_x xp_{X}(x) = \sum_x x\sum_{i=1}^n P(A_i)p_{X|A_i}(x)
= \sum_{i=1}^n P(A_i)\sum_x x p_{X|A_i}(x)
= \sum_{i=1}^n P(A_i)E[X|A_i]
E[X]
Instead of conditioning on events we can also condition on random variables
E[X]
= \sum_{y} p_Y(y)E[X|Y=y]
Total Expectation Theorem
E[X] = \sum_x xp_X(x)
time taken


0.5
0.3
0.2

X:
E[X|A_1] = 60 mins
E[X|A_2] = 30 mins
E[X|A_3] = 45 mins
E[X] = ?
\sum_{i=1}^{3}P(A_i)E[X|A_i]
Expectation: Mult. rand. variables
Example: You lose INR 1 if the number on die 1 is less than that on die 2 and win INR 1 otherwise
E[g(X)] = \sum_x g(x)p_X(x)
g(X,Y) = \begin{cases}
-1~if X < Y\\
+1~if X \geq Y
\end{cases}
E[g(X,Y)] = ?
How do you compute this without computing the distribution of \(g(X,Y)\)?
Expectation: Mult. rand. variables
E[g(X)] = \sum_x g(x)p_X(x)
E[g(X,Y)] = \sum_{y} p_Y(y) E [g(X,Y)|Y=y]
= \sum_{y} p_Y(y) E [g(X,y)|Y=y]
= \sum_{y} p_Y(y) \sum_{x} g(x,y)p_{X|Y}(x|y)
= \sum_{x} \sum_{y} p_Y(y) g(x,y)p_{X|Y}(x|y)
= \sum_{x} \sum_{y} g(x,y)p_{X,Y}(x,y)
Expectation: Mult. rand. variables
Example: You lose INR 1 if the number on die 1 is less than that on die 2 and win INR 1 otherwise
g(X,Y) = \begin{cases}
-1~if X < Y\\
+1~if X \geq Y
\end{cases}
E[g(X,Y)] = \sum_x\sum_y g(x,y)p_{X,Y}(x,y)
p_X(x,y) = \frac{1}{36} \forall x,y
= \frac{1}{6}
Expectation: Mult. rand. variables
In general,
E[g(X,Y)] \neq g(E[X],E[Y])
Exception 1
E[g(X,Y)]
g(X,Y) = aX + bY
E[g(X,Y)] = \sum_x\sum_y g(x,y)p_X(x,y)
= \sum_x\sum_y (ax + by)p_X(x,y)
= a \sum_x x \sum_y p_X(x,y) + b \sum_y y \sum_x p_X(x,y)
\underbrace{~~~~~~~~~~~~~~~~~~~~}
\underbrace{~~~~~~~~~~~~~~~~~~~~~}
= a \sum_x x p_X(x) + b \sum_y y p_Y(y)
= a E[X] + b E[Y]
= g(E[X], E[Y])
= \sum_x\sum_y g(x,y)p_X(x,y)
\underbrace{~~~~~~~~~~}
\underbrace{~~~~~~~~~~}
Expectation: Mult. rand. variables
In general,
E[g(X,Y)] \neq g(E[X],E[Y])
Exception 2
E[g(X,Y)]
g(X,Y) = XY
E[g(X,Y)] = \sum_x\sum_y g(x,y)p_X(x,y)
= \sum_x\sum_y g(x,y)p_X(x,y)
\(X,Y\) are independent
= \sum_x\sum_y xyp_X(x)p_Y(y)
= \sum_x xp_X(x) \sum_y yp_Y(y)
= E[X]E[Y]
= g(E[X],E[Y])
\underbrace{~~~~~~~~~~~~~~~~~~~}
\underbrace{~~~~~~~~~~~~~~~~~~~}
Variances: Mult. rand. variables
Recap,
Var(aX) = a^2 Var(X)
E[g(X,Y)] = \sum_x\sum_y g(x,y)p_X(x,y)
Var(X+a) = Var(X)
In general,
Var(X+Y) \neq Var(X) + Var(Y)
Examples, X = Y, X = -Y
Exception: If \(X\) and \(Y\) are independent
Var(X+Y) = E [(X+Y)^2] - (E[X+Y])^2
Variances: Mult. rand. variables
Proof: (given: \(X~and~Y\) are independent)
E[g(X,Y)] = \sum_x\sum_y g(x,y)p_X(x,y)
Var(X+Y) = E [(X+Y)^2] - (E[X+Y])^2
= E [X^2 + 2XY + Y^2] - (E[X] + E[Y])^2
= E [X^2] + 2E[XY] + E[Y^2] - (E[X]^2 + 2E[X]E[Y] + E[Y]^2)
= E [X^2] + 2E[X]E[Y] + E[Y^2] - E[X]^2 - 2E[X]E[Y] - E[Y]^2
= E [X^2] - E[X]^2 + E[Y^2] - E[Y]^2
= Var(X) + Var(Y)
Where did we use the independence property?
Summary of main results
X
X|Y
X, Y
E[X] = \sum_x xp_X(x)
"long term" average
E[g(X)] = \sum_x g(x)p_X(x)
function of RV
E[a X + b] = a E[X] + b
linearity of expectation
Var(X) = E[(X - E[X])^2]
spread in the data
Var(a X + b) = a^2 Var(X)
E[X|A] = \sum_x xp_{X|A}(x)
conditioned on event
E[X|Y] = \sum_x xp_{X|Y}(x|y)
conditioned on RV
E[g(X)|A] = \sum_x g(x)p_{X|A}(x)
E[g(X)|Y=y] = \sum_x g(x)p_{X|Y}(x|y)
E[X] = \sum_{i=1}^n P(A_i)E[X|A_i]
E[X] = \sum_{y} p_Y(y)E[X|Y=y]
total expectation theorem
E[g(X,Y)] = \sum_x\sum_y g(x,y)p_X(x,y)
function of multiple RVs
E[g(X,Y)] \neq g(E[X],E[Y])
in general, not equal but
E[aX+bY)] = aE[X] + b E[Y]
E[XY)] = E[X]E[Y]
if \(X\) and \(Y\) are independent
Var(X+Y) = Var(X) + Var(Y)