CS6015: Linear Algebra and Random Processes
Lecture 36: Uniform distribution, Normal distribution
Learning Objectives
What is the uniform distribution?
What is the normal distribution?
What are some properties of the normal distribution?
Uniform distribution (continuous)
Discrete Uniform Distribution
\frac{1}{b - a}
b
p_X(x)
f_X(x)
Continuous Uniform Distribution
a_1
b_1
[
]
P(a_1 \leq X \leq b_1) = \frac{1}{b-a} (b_1 - a_1)
a
b
\dots
\dots
\frac{1}{b - a + 1}
a
b
Expectation

f_X(x)
p_X(x)
a
b
\dots
\dots
\frac{1}{b - a + 1}
E[X] = \sum_x xp_X(x)
E[g(X)] = \sum_x g(x) p_X(x)
Var(X) = E[X^2] - (E[X])^2
E[X] = \int_{-\infty}^{\infty} xf_X(x) dx
E[g(X)] = \int_{-\infty}^{\infty}g(x) p_X(x)dx
Var(X) = E[X^2] - (E[X])^2
Mean and variance (Uniform Distribution)
E[X] = \int_{a}^{b} x\frac{1}{b-a} dx
E[g(X)] = \int_{-\infty}^{\infty}g(x) p_X(x) dx
Var(X) = E[X^2] - (E[X])^2
\frac{1}{b - a}
b
f_X(x)
a
b
=\frac{a+b}{2}
E[X] = \int_{-\infty}^{\infty} xf_X(x) dx
E[X^2] = \int_{a}^{b} x^2\frac{1}{b-a} dx
=\frac{1}{b-a}(\frac{b^3}{3} - \frac{a^3}{3})
Var(X) = E[X^2] - (E[X])^2 = \frac{(b-a)^2}{12}
E[X] = \int_{a}^{b} x\frac{1}{b-a} dx
E[X^2] = \int_{a}^{b} x^2\frac{1}{b-a} dx
E[X] =\frac{1}{b-a} * \frac{x^2}{2} |_{a}^b
= \frac{1}{b-a} * (\frac{b^2}{2} - \frac{a^2}{2}) = \frac{1}{b-a}\frac{b^2 - a^2}{2}
= \frac{1}{b-a}\frac{(b - a)(b+a)}{2} = \frac{a+b}{2}
=\frac{1}{b-a} * \frac{x^3}{3} |_{a}^b
= \frac{1}{b-a} * (\frac{b^3}{3} - \frac{a^3}{3}) = \frac{1}{b-a}\frac{b^3 - a^3}{3}
= \frac{1}{b-a}\frac{(b - a)(a^2 + ab + b^2)}{3} = \frac{a^2 + ab + b^2}{3}
Var(X) = E[X^2] - E[X]^2
= \frac{a^2 + ab + b^2}{3} - (\frac{a+b}{2})^2
= \frac{a^2 + ab + b^2}{3} - \frac{a^2 + 2ab + b^2}{4}
= \frac{(b-a)^2}{12}
Normal Distribution
Some fun with functions

x^2
e^x

x



e^{-x}
e^{x^2}
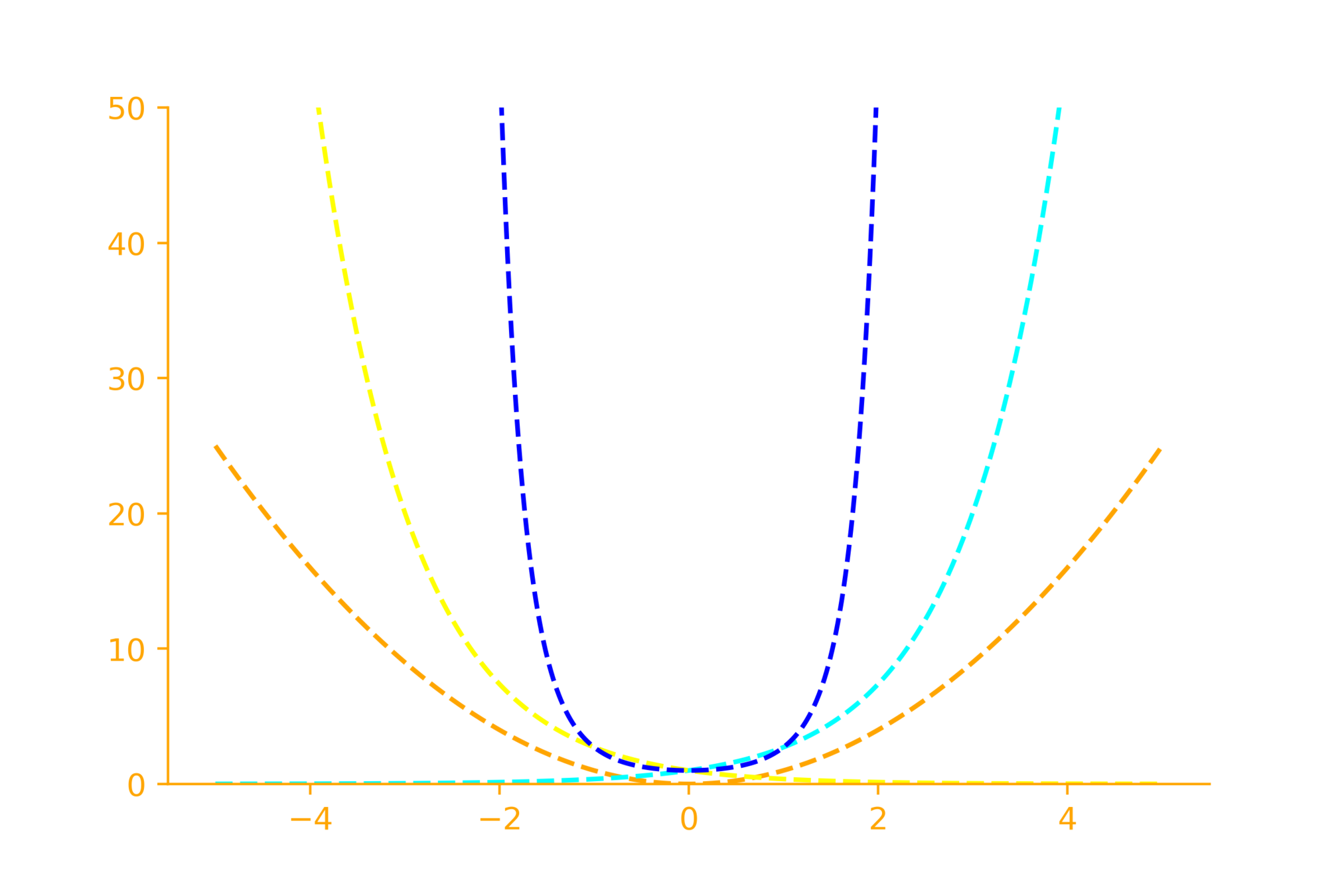
e^{-x^2}


20 * e^{-x^2}
Some fun with functions
e^{-x^2}








Normal distribution
\mathcal{N}(0, 1) = \frac{1}{\sqrt{2 \pi}}e^{-x^2}








\int_{-\infty}^{\infty} \frac{1}{\sqrt{2 \pi}}e^{-x^2} dx = 1
Normal distribution
\mathcal{N}(0, 1) = \frac{1}{\sqrt{2 \pi}}e^{-x^2}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{-x^2} dx
= 0
Var[X] = E[X^2] - (E[X])^2

= 1
zero mean, unit variance
\mu = 0, \sigma = 1
Normal distribution (changing
\mathcal{N}(\mu, 1) = \frac{1}{\sqrt{2 \pi}}e^{-\frac{(x-\mu)^2}{2}}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{-\frac{(x-\mu)^2}{2}} dx
= \mu
Var[X] = E[X^2] - (E[X])^2

= 1
\mu = 2

\mu = 0
\mu = -2

\mu)
Normal distribution (changing
\mathcal{N}(0, \sigma^2) = \frac{1}{\sqrt{2 \pi}}e^{\frac{-x^2}{2\sigma^2}}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{\frac{-x^2}{2\sigma^2}} dx
= 0
Var[X] = E[X^2] - (E[X])^2
= \sigma^2
\sigma = 0.5
\sigma = 1
\sigma = 2
\sigma)



Normal distribution (changing
\mathcal{N}(\mu, \sigma^2) = \frac{1}{\sqrt{2 \pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}}
E[X] = \int_{-\infty}^{\infty}x\cdot\frac{1}{\sqrt{2 \pi}}e^{\frac{-(x-\mu)^2}{2\sigma^2}} dx
= \mu
Var[X] = E[X^2] - (E[X])^2
\mu = 2, \sigma = 0.5
\mu, \sigma)

= \sigma^2
The distribution is fully specified by the parameters:
\mu, \sigma^2
Normal distribution
\sigma
\sigma
\sigma
\sigma
\sigma
\sigma
\sigma
\sigma
68\%
95\%
99\%
P(\mu - \sigma \leq X \leq \mu + \sigma)
= \int_{\mu - \sigma}^{\mu + \sigma} \frac{1}{\sqrt{2\pi}} e^{ \frac{-(x - \mu)}{2 \sigma^2} } dx

\approx 0.68
P(\mu - 2\sigma \leq X \leq \mu + 2\sigma)
= \int_{\mu - 2\sigma}^{\mu + 2\sigma} \frac{1}{\sqrt{2\pi}} e^{ \frac{-(x - \mu)}{2 \sigma^2} } dx
\approx 0.95