CS6015: Linear Algebra and Random Processes
Lecture 6: Vector spaces, subspaces, independence, span, basis, dimensions
Learning Objectives
What is a vector space and a subspace?
What is the basis of a space/subspace?
What is the span of a set of vectors?
What are independent vectors?
What is the dimension of a space/subspace?
(for today's lecture)
The bigger picture
\begin{bmatrix}
~~~&~~~&~~~\\
~~~&~~~&~~~\\
~~~&~~~&~~~\\
\end{bmatrix}
m < n
m=n
\begin{bmatrix}
~~~&~~~&~~~&~~~&~~~\\
~~~&~~~&~~~&~~~&~~~\\
~~~&~~~&~~~&~~~&~~~\\
\end{bmatrix}
\begin{bmatrix}
~~~&~~~&\\
~~~&~~~&\\
~~~&~~~&\\
~~~&~~~&\\
~~~&~~~&\\
~~~&~~~&
\end{bmatrix}
m > n
rank =
A
A
A
Q1. For which b's does a solution not exist?
0,1,\infty~solutions
Q2. Which x's are a solution for Ax = 0?
Q3. What's the connection between these two Qs?
A\mathbf{x}=\mathbf{b}
n pivots
1 unique solution
Find L,U
Or find
A^{-1}

Vector spaces
Why this detour?
All b's for which a solution to Ax=b exists
(well, it's not really a detour)
We need some vocabulary to specify:
All x's which are a solution to Ax=0
[Answer: some vector (sub)space]
[Answer: some vector (sub)space]
We will spend some time in learning this vocabulary (concepts)!
Recap: What do you do with vectors?
Linear equations
\mathbf{x} =\begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix}
\mathbf{y} =\begin{bmatrix}
y_1 \\ y_2 \\ y _3
\end{bmatrix} \in \mathbb{R}^3
Add
\mathbf{x} + \mathbf{y} =\begin{bmatrix}
x_1 + y_1 \\ x_2 + y_2 \\ x_3 + y_3
\end{bmatrix} \in \mathbb{R}^3
Scale
a\mathbf{x} =\begin{bmatrix}
ax_1 \\ ax_2 \\ ax_3
\end{bmatrix}
=a\begin{bmatrix}
x_1 \\ x_2 \\ x_3
\end{bmatrix} \in \mathbb{R}^3
Linear combinations
a\mathbf{x} + b\mathbf{y}=\begin{bmatrix}
ax_1 + by_1\\ ax_2 + by_2\\ ax_3 + by_3
\end{bmatrix}
Vector Spaces
Linear equations
\mathbf{u},\mathbf{v},\mathbf{w} \in V
a,b \in \mathbb{R}~(scalars)
(definitions and properties)
V
A vector space is a collection of vectors which can be added together and be multiplied by scalars (i.e., we can take linear combinations)

\mathbf{u}+(\mathbf{v}+\mathbf{w}) = (\mathbf{u}+\mathbf{v})+\mathbf{w}
\mathbf{u}+\mathbf{v} = \mathbf{v}+\mathbf{u}
\mathbf{v}+\mathbf{0} = \mathbf{v}
\mathbf{v}+\mathbf{-v} = \mathbf{0}
Addition properties
a(b\mathbf{v}) = (ab)\mathbf{v}
1(\mathbf{v}) = \mathbf{v}
a(\mathbf{u} + \mathbf{v}) = a\mathbf{u} + a\mathbf{v}
(a + b)\mathbf{v} = a\mathbf{v} + b\mathbf{v}
Multiplication properties
Closure Properties
\mathbf{u} + \mathbf{v} \in V
a\mathbf{u} \in V
a\mathbf{u} + b\mathbf{v} \in V
Examples of Vector Spaces
Linear equations
(that we care about)
\mathbb{R}
\mathbb{R}^2
\mathbb{R}^3
\mathbb{R}^n
\cdots
\begin{bmatrix}
1 \\ 2 \\ 3
\end{bmatrix}
\begin{bmatrix}
2 \\ 1 \\ 4
\end{bmatrix}
\begin{bmatrix}
0 \\ 0 \\ 0
\end{bmatrix}
\cdots
\cdots

We will take these for granted
This is what we will really worry about
a\mathbf{u} + b\mathbf{v} \in V
Subset of a Vector Space
Linear equations

What if we remove one vector from
a\mathbf{u} + b\mathbf{v} \in V
\mathbb{R}^3
(say, the 0 vector) ?
Is this subset a vector space?
(we get a subset of )
\mathbb{R}^3
(clearly not: )
a\mathbf{u} \notin V~for~a=0
Can we think of a subset of \(\mathbb{R}^3\) that still satisfies the requirements of a vector space?
Subspaces
Linear equations
A subspace is a non-empty subset of a vector space that still satisfies the requirements of a vector space

Closure Properties
\mathbf{u} + \mathbf{v} \in S
a\mathbf{u} \in S
a\mathbf{u} + b\mathbf{v} \in S
if~\mathbf{u}, \mathbf{v} \in S
(of course, the addition and multiplication properties should also be satisfied)
Examples of subspaces
Linear equations
Let~V = \mathbb{R}^2
(i.e., the original space)

We are looking for subspaces of this space
The \(\mathbf{0}\) vector is a subspace (trivial)
u=\begin{bmatrix}
4\\4
\end{bmatrix}
Is \(S = \{\mathbf{u}\} \) a subspace?
(clearly not: )
a\mathbf{u} \notin S~for~a=0
What should we add to \(S \) to make it a subspace?
\mathbf{0}
2\mathbf{u}
3\mathbf{u}
4\mathbf{u}
\dots
(all multiples of )
\mathbf{u}
Examples of subspaces
Linear equations

What are the possible subspaces of \(\mathbb{R}^2\) ?
The \(\mathbf{0}\) vector (trivial)

u=\begin{bmatrix}
4\\4
\end{bmatrix}
Any line passing through the origin
The whole of \(\mathbb{R}^2\)
(all multiples of any vector )
\mathbf{u}
Note that the \(\mathbb{0}\) vector will always be a part of any subspace
(if~\mathbf{u} \in S~then~0\cdot\mathbf{u}=\mathbf{0}~must~be~\in S)
Examples of subspaces
Linear equations

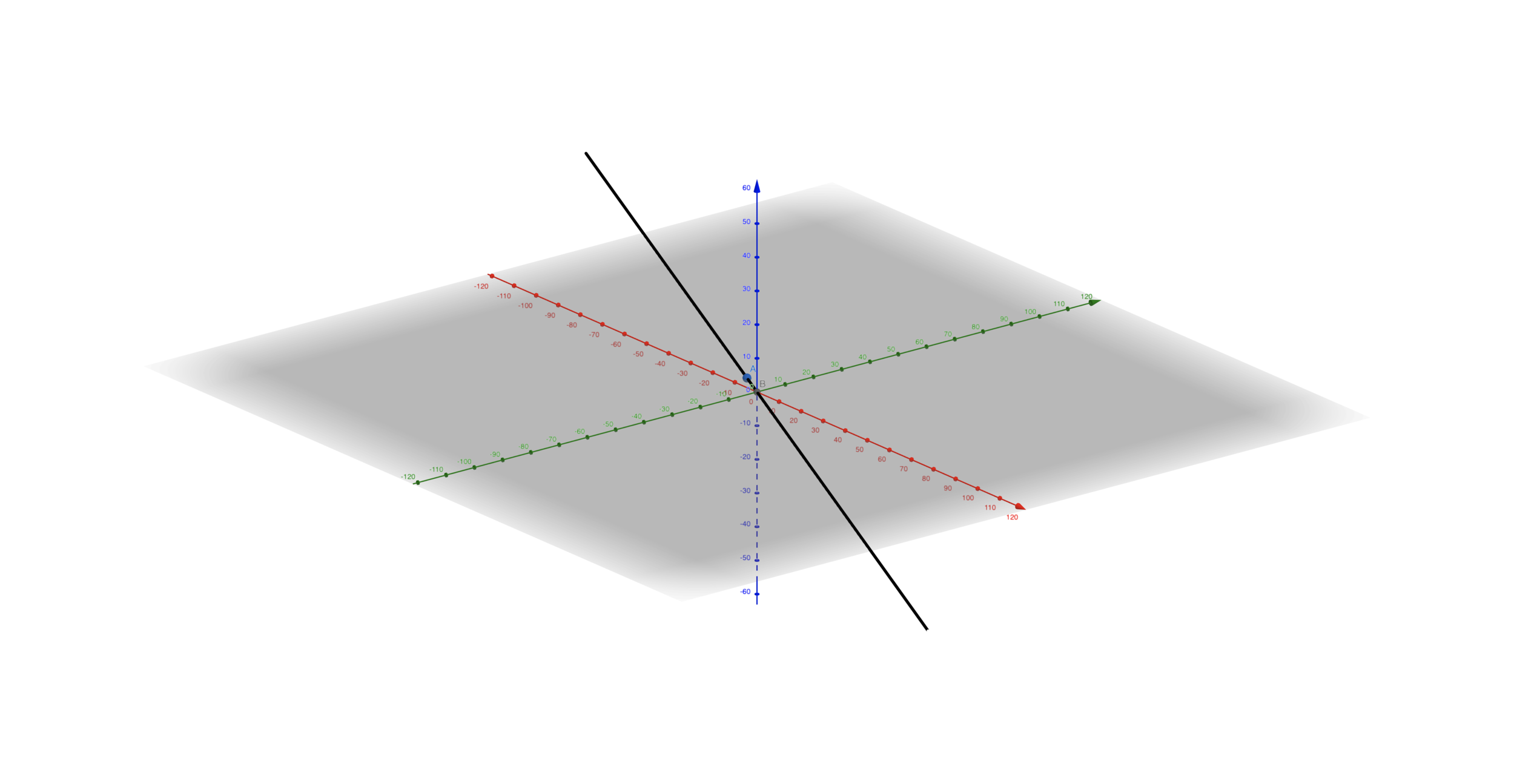
What are the possible subspaces of \(\mathbb{R}^3\) ?
\mathbf{u}
Examples of subspaces
Linear equations

What are the possible subspaces of \(\mathbb{R}^3\) ?
The \(\mathbf{0}\) vector (trivial)
The whole of \(\mathbb{R}^3\)
(all multiples of any vector \(\mathbf{u}\)
Note that the \(\mathbb{0}\) vector will always be a part of any subspace
Any line passing through the origin
(all linear combinations of )
Any plane passing through the origin
\mathbf{u},\mathbf{v}
(if~\mathbf{u} \in S~then~0\cdot\mathbf{u}=\mathbf{0}~must~be~\in S)

Examples of subspaces
Linear equations

Possible subspaces of \(\mathbb{R}^3\)
Puzzles: complete these subspaces
Linear equations
\mathbf{u}=\begin{bmatrix}
1\\
-1\\
2
\end{bmatrix}
\mathbf{v}=\begin{bmatrix}
2\\
2\\
1
\end{bmatrix}
\mathbf{w}=\begin{bmatrix}
1\\
1\\
3
\end{bmatrix}
a\mathbf{u}
\forall a \in \mathbb{R}
\mathbf{u}=\begin{bmatrix}
1\\
-1\\
2
\end{bmatrix}
a\mathbf{u} + b\mathbf{v}
\forall a,b \in \mathbb{R}
\mathbf{v}=\begin{bmatrix}
2\\
2\\
1
\end{bmatrix}
\mathbf{u}=\begin{bmatrix}
1\\
-1\\
2
\end{bmatrix}
a\mathbf{u} + b\mathbf{v} + c\mathbf{w}
\forall a,b,c \in \mathbb{R}
What kind of a surface would it be?
(line)
(2d plane)
whole of
\mathbb{R}^3
Puzzles: complete these subspaces
Linear equations
\mathbf{u}=\begin{bmatrix}
1\\
-1\\
2\\
1
\end{bmatrix}
\mathbf{v}=\begin{bmatrix}
2\\
2\\
1\\
1
\end{bmatrix}
\mathbf{w}=\begin{bmatrix}
1\\
1\\
3\\
1
\end{bmatrix}
a\mathbf{u}
\forall a \in \mathbb{R}
\mathbf{u}=\begin{bmatrix}
1\\
-1\\
2\\
1
\end{bmatrix}
a\mathbf{u} + b\mathbf{v}
\forall a,b \in \mathbb{R}
\mathbf{v}=\begin{bmatrix}
2\\
2\\
1\\
1
\end{bmatrix}
\mathbf{u}=\begin{bmatrix}
1\\
-1\\
2\\
1
\end{bmatrix}
a\mathbf{u} + b\mathbf{v} + c\mathbf{w}
\forall a,b,c \in \mathbb{R}
What kind of a surface would each of it be?
(line)
(2d plane)
(3d hyperplane)
Puzzles: what is the subspace?
Linear equations
\mathbf{u}=\begin{bmatrix}
1\\
1\\
1\\
1
\end{bmatrix}
\mathbf{v}=\begin{bmatrix}
1\\
2\\
3\\
4
\end{bmatrix}
\implies a\mathbf{u} + b\mathbf{v} + c\mathbf{w} + d \mathbf{z} \in S
\forall a,b,c,d \in \mathbb{R}
\mathbf{w}=\begin{bmatrix}
-1\\
-1\\
-1\\
-1
\end{bmatrix}
\mathbf{z}=\begin{bmatrix}
-1\\
-2\\
-3\\
-4
\end{bmatrix}
\(\mathbf{u,v,w,z} \in S\)
\implies a\mathbf{u} + b\mathbf{v} + c(-\mathbf{u}) + d (-\mathbf{v}) \in S
\implies (a-c)\mathbf{u} + (b-d)\mathbf{v} \in S
all linear combinations of 2 vectors: a 2d plane
Puzzles: what is the subspace?
Linear equations
\mathbf{u}=\begin{bmatrix}
1\\
1\\
1\\
1
\end{bmatrix}
\mathbf{v}=\begin{bmatrix}
1\\
2\\
3\\
4
\end{bmatrix}
\implies a\mathbf{u} + b\mathbf{v} + c\mathbf{w} + d \mathbf{z} \in S
\forall a,b,c,d \in \mathbb{R}
\mathbf{w}=\begin{bmatrix}
-1\\
-1\\
-1\\
-1
\end{bmatrix}
\mathbf{z}=\begin{bmatrix}
2\\
3\\
4\\
5
\end{bmatrix}
\(\mathbf{u,v,w,z} \in S\)
\implies a\mathbf{u} + b\mathbf{v} + c(-\mathbf{u}) + d (\mathbf{u}+\mathbf{v}) \in S
\implies (a-c+d)\mathbf{u} + (b+d)\mathbf{v} \in S
all linear combinations of 2 vectors: a 2d plane
Puzzles: what is the subspace?
Linear equations
\mathbf{u}\in \mathbb{R}^5
\implies a\mathbf{u} + b\mathbf{v} + c\mathbf{w} + d \mathbf{y} + e \mathbf{z} \in S
\forall a,b,c,d,e \in \mathbb{R}
\(\mathbf{u,v,w,y,z} \in S\)
\implies a\mathbf{u} + b\mathbf{v} + c(a\mathbf{u}) + d (b\mathbf{u}+c\mathbf{v}) + e(d\mathbf{v}) \in S
\implies (a+ac+db)\mathbf{u} + (b+dc+ed)\mathbf{v} \in S
all linear combinations of 2 vectors: a 2d plane
,\mathbf{v}\in \mathbb{R}^5
,\mathbf{w}=a\mathbf{u}, \mathbf{y}=b\mathbf{u} + c\mathbf{v}, \mathbf{z}=d\mathbf{v}
(5 vectors)
\(\mathbf{w,y,z}\) are dependent on \(\mathbf{u,v}\)
Demo: Linear combination
Linear equations
Independent Vectors
Linear equations
We say that \(\mathbf{v_1}, \mathbf{v_2}, \mathbf{v_3}, \dots, \mathbf{v_n} \in \mathbb{R}^n\) are independent if no combination of these vectors gives the \( \mathbf{0} \) vector (except the 0 combination)
c_1\mathbf{v_1}+c_2\mathbf{v_2}+c_3\mathbf{v_3}+\dots+c_n\mathbf{v_n}=0~only~if~c_i=0~\forall i
The vector \(\mathbf{v_k}\) is dependent on \(\mathbf{v_1}, \mathbf{v_2}, \mathbf{v_3}, \dots, \mathbf{v_n}\) if it can be expressed as a linear combination of these vectors
Span
Linear equations
\mathbf{v_1}, \mathbf{v_2}, \mathbf{v_3}, \dots, \mathbf{v_n} \in V
We say that \(\mathbf{v_1}, \mathbf{v_2}, \mathbf{v_3}, \dots, \mathbf{v_n}\) span \(V\) if every vector in \(V\) can be written as a linear combination of these vectors
Examples:
\begin{bmatrix}
1\\0
\end{bmatrix}
\begin{bmatrix}
0\\1
\end{bmatrix}
span \(\mathbb{R}^2\)
\begin{bmatrix}
1\\0\\0
\end{bmatrix}
\begin{bmatrix}
0\\1\\0
\end{bmatrix}
span \(\mathbb{R}^3\)
\begin{bmatrix}
0\\0\\1
\end{bmatrix}
\begin{bmatrix}
2\\3
\end{bmatrix}
\begin{bmatrix}
1\\2
\end{bmatrix}
span \(\mathbb{R}^2\)
span \(\mathbb{R}^3\)
\begin{bmatrix}
1\\1\\1
\end{bmatrix}
\begin{bmatrix}
1\\2\\3
\end{bmatrix}
\begin{bmatrix}
3\\4\\1
\end{bmatrix}
Basis of a space
Linear equations
We say that \(\mathbf{v_1}, \mathbf{v_2}, \mathbf{v_3}, \dots, \mathbf{v_n} \in V\) form the basis of \(V\) if
\begin{bmatrix}
1\\0\\0
\end{bmatrix}
\begin{bmatrix}
0\\1\\0
\end{bmatrix}
span \(\mathbb{R}^3\)
\begin{bmatrix}
0\\0\\1
\end{bmatrix}
\begin{bmatrix}
1\\1\\1
\end{bmatrix}
\begin{bmatrix}
1\\2\\3
\end{bmatrix}
\begin{bmatrix}
3\\4\\1
\end{bmatrix}
but we don't need all of them
the last 3 vectors are dependent on the first 3
these vectors are independent
these vectors span the space \(V\)
\mathbf{v_1}, \mathbf{v_2}, \mathbf{v_3}, \dots, \mathbf{v_n} \in V
Basis of a space
Linear equations
Examples:
\begin{bmatrix}
1\\0
\end{bmatrix}
\begin{bmatrix}
0\\1
\end{bmatrix}
\begin{bmatrix}
1\\0\\0
\end{bmatrix}
\begin{bmatrix}
0\\1\\0
\end{bmatrix}
\begin{bmatrix}
0\\0\\1
\end{bmatrix}
\begin{bmatrix}
2\\3
\end{bmatrix}
\begin{bmatrix}
1\\2
\end{bmatrix}
\begin{bmatrix}
1\\1\\1
\end{bmatrix}
\begin{bmatrix}
1\\2\\3
\end{bmatrix}
\begin{bmatrix}
3\\4\\1
\end{bmatrix}
Basis of \(\mathbb{R}^2\)
Basis of \(\mathbb{R}^3\)
\begin{bmatrix}
1\\1\\1
\end{bmatrix}
\begin{bmatrix}
1\\2\\3
\end{bmatrix}
\begin{bmatrix}
3\\4\\1
\end{bmatrix}
\begin{bmatrix}
1\\0\\0
\end{bmatrix}


Same space can have multiple basis
Every basis of a space will have the same number of vectors (dimension of the space)




A puzzle
Linear equations
\mathbf{u}=\begin{bmatrix}
1\\1\\1
\end{bmatrix}
\mathbf{v}=\begin{bmatrix}
1\\2\\3
\end{bmatrix}

What is the span?
Can you think of an alternative basis?
What is the dimension of the spanned subspace?
c\mathbf{u} + d\mathbf{v}~~\forall c,d \in \mathbb{R}
2\mathbf{u}, 3\mathbf{v}
2
a 2 dimensional plane
How many vectors in the basis of \(\mathbb{R}^n\) ?
n