CS6015: Linear Algebra and Random Processes

Lecture 9: Solving Ax=b, Rank Nullity Theorem, Some unsolved mysteries

Learning Objectives

How do you find one solution for Ax=b? (if it exists)

What is the connection between rank and number of solutions?

How do you find all solutions for Ax =b?

(for today's lecture)

A couple of unsolved mysteries!

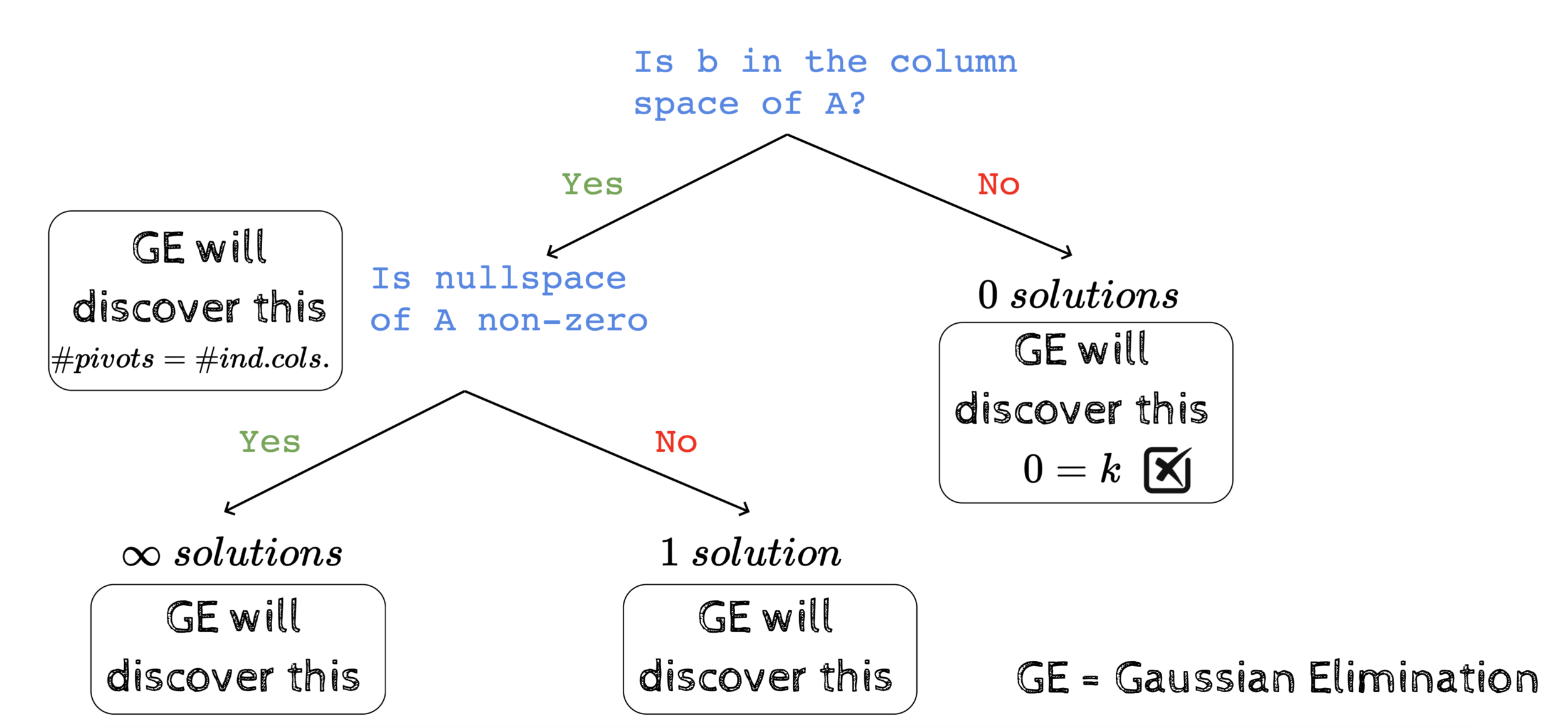
Recap: Two possibilities

Solution does not exist

GE will discover this

Solution exists

GE will discover this

We will now see how to find the solutions

(ridiculously easy)
0=1
\begin{bmatrix} 1&1&2\\ 0&1&1\\ 0&0&0\\ 0&0&0\\ \end{bmatrix}
\mathbf{x}
=\begin{bmatrix} 1\\ 1\\ 0\\ 1 \end{bmatrix}
0=0
\begin{bmatrix} 1&1&2\\ 0&1&1\\ 0&0&0\\ 0&0&0\\ \end{bmatrix}
\mathbf{x}
=\begin{bmatrix} 1\\ 1\\ 0\\ 0 \end{bmatrix}

Solving Ax = b

\begin{bmatrix} 1&1&2\\ 1&2&3\\ 1&3&4\\ 1&4&5\\ \end{bmatrix}
\mathbf{x}
=\begin{bmatrix} 1\\ 2\\ 3\\ 4 \end{bmatrix}

Gauss Elimination

Set the free variables to 0

Why is it okay to do this?

Solve for pivot variables by back-substitution

x_1+x_2+2x_3 = 1
x_2+x_3 = 1
x_2+ 0 = 1
\therefore x_2 = 1
x_1+1+2(0) = 1
\therefore x_1 = 0
\mathbf{x}_{particular}=\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}
if we can write b as a linear combination of the 3 columns then we should also be able to write it as a linear combination of the 2  pivot/independent columns (the third column is redundant as it does not add any new information)
\begin{bmatrix} 1&1&2\\ 0&1&1\\ 0&0&0\\ 0&0&0\\ \end{bmatrix}
=\begin{bmatrix} 1\\ 1\\ 0\\ 0 \end{bmatrix}
\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}

Pivot columns

\underbrace{~~~~~~~~~~}
\underbrace{~}

Free columns

Solving Ax = b

\begin{bmatrix} 1&1&2\\ 1&2&3\\ 1&3&4\\ 1&4&5\\ \end{bmatrix}
\mathbf{x}
=\begin{bmatrix} 1\\ 2\\ 3\\ 4 \end{bmatrix}

Gauss Elimination

\mathbf{x}_{particular}=\begin{bmatrix} 0\\ 1\\ 0 \end{bmatrix}

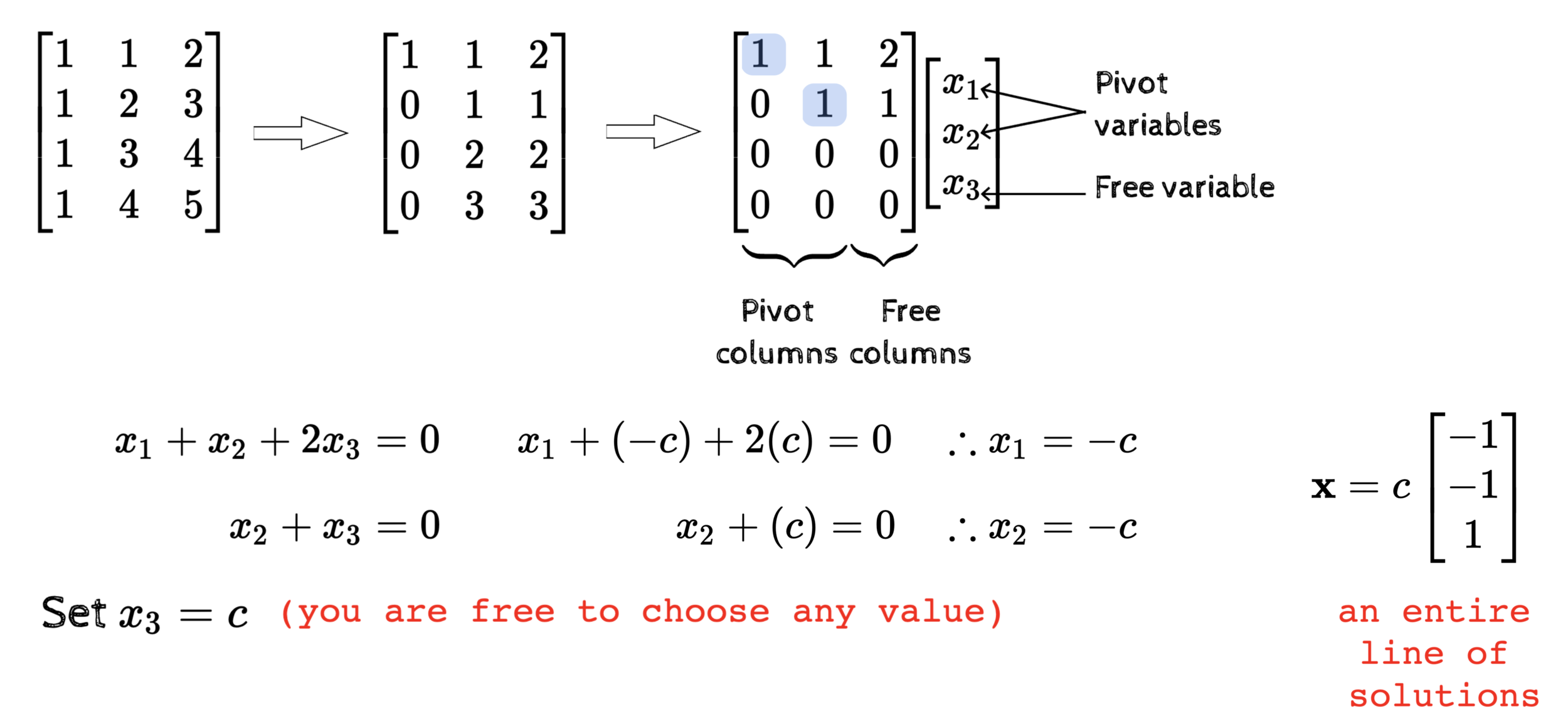
(the complete solution)

\mathbf{x}_{complete}=\mathbf{x}_{particular} + \mathbf{x}_{nullspace}
\mathbf{x}_{complete}=
+~~~c\begin{bmatrix} -1\\ -1\\ 1\end{bmatrix}
\begin{bmatrix} 0\\1\\0 \end{bmatrix}
A
A
A
=
\mathbf{b}
+~~\mathbf{0}
\begin{bmatrix} 1&1&2\\ 0&1&1\\ 0&0&0\\ 0&0&0\\ \end{bmatrix}
=\begin{bmatrix} 1\\ 1\\ 0\\ 0 \end{bmatrix}
\begin{bmatrix} x_1\\ x_2\\ x_3 \end{bmatrix}

Pivot columns

\underbrace{~~~~~~~~~~}
\underbrace{~}

Free columns

Solving Ax = b

\mathbf{x}_{particular}=\begin{bmatrix} -3\\ 8\\ 0\\ 0\\ \end{bmatrix}

(another example)

\begin{bmatrix} 1&1&1&1\\ 1&2&3&4\\ 2&3&4&5 \end{bmatrix}
=\begin{bmatrix} 5\\ 13\\ 18 \end{bmatrix}
\mathbf{x}

Gauss Elimination

x_1+x_2+x_3+x_4 = 5
x_2+2x_3+3x_4 = 8
\therefore x_2 = 8
\therefore x_1 = -3

Set the free variables to 0

Solve for pivot variables by back-substitution

x_1+8+0+0 = 5
x_2+2(0)+3(0)= 8

Pivot columns

\underbrace{~~~~~~~~~~}

Free columns

\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}
\begin{bmatrix} 1&1&1&1\\ 0&1&2&3\\ 0&0&0&0 \end{bmatrix}
\underbrace{~~~~~~~~~~}
=\begin{bmatrix} 5\\ 8\\ 0 \end{bmatrix}

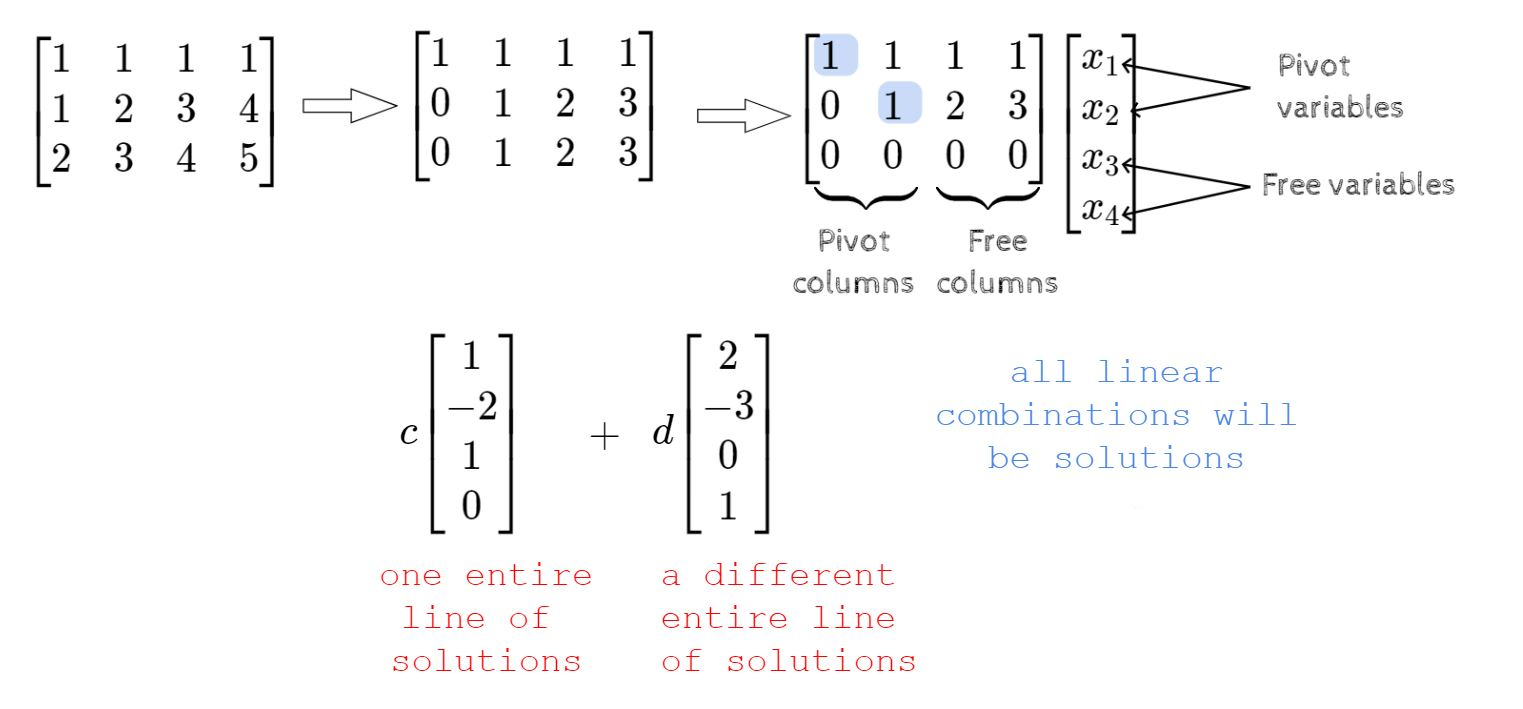
Solving Ax = b

(another example)

\mathbf{x}_{complete}=\mathbf{x}_{particular} + \mathbf{x}_{nullspace}
\mathbf{x}_{complete}= \begin{bmatrix} -3\\ 8\\ 0\\ 0\\ \end{bmatrix}
+~c\begin{bmatrix} 1\\ -2\\ 1\\ 0 \end{bmatrix} +~d\begin{bmatrix} 2\\ -3\\ 0\\ 1 \end{bmatrix}
\begin{bmatrix} 1&1&1&1\\ 1&2&3&4\\ 2&3&4&5 \end{bmatrix}

Pivot columns

\underbrace{~~~~~~~~~~}

Free columns

\begin{bmatrix} x_1\\ x_2\\ x_3\\ x_4 \end{bmatrix}
=\begin{bmatrix} 5\\ 13\\ 18 \end{bmatrix}
\begin{bmatrix} 1&1&1&1\\ 0&1&2&3\\ 0&0&0&0 \end{bmatrix}
\underbrace{~~~~~~~~~~}
\mathbf{x}

Gauss Elimination

=\begin{bmatrix} 5\\ 8\\ 0 \end{bmatrix}

Solving Ax = b

(the geometric view)

(switch to geogebra)

\mathbf{x}_{complete}=
+~~~c\begin{bmatrix} -1\\ -1\\ 1\end{bmatrix}
\begin{bmatrix} 0\\1\\0 \end{bmatrix}

Nullspace: all the multiples of vector (-1,-1,1), Particular solution: vector (0,1,0)

Solving Ax = b

(the geometric view)

Nullspace: xy plane , Particular solution: vector (1,1,1)

Solving Ax = b

(the geometric view)

Rank of a matrix

What does the rank tell us about the number of solutions?

rank

= number of independent rows            = number of non-zero pivots after GE = number of independent columns

(everything)

Pivot columns

Free columns

rank < n,m

Non-zero pivots

zero pivots

rows with all 0s after GE

Things that we know so far....

Rows with zeros \(\implies \) it is possible that there are 0 solutions

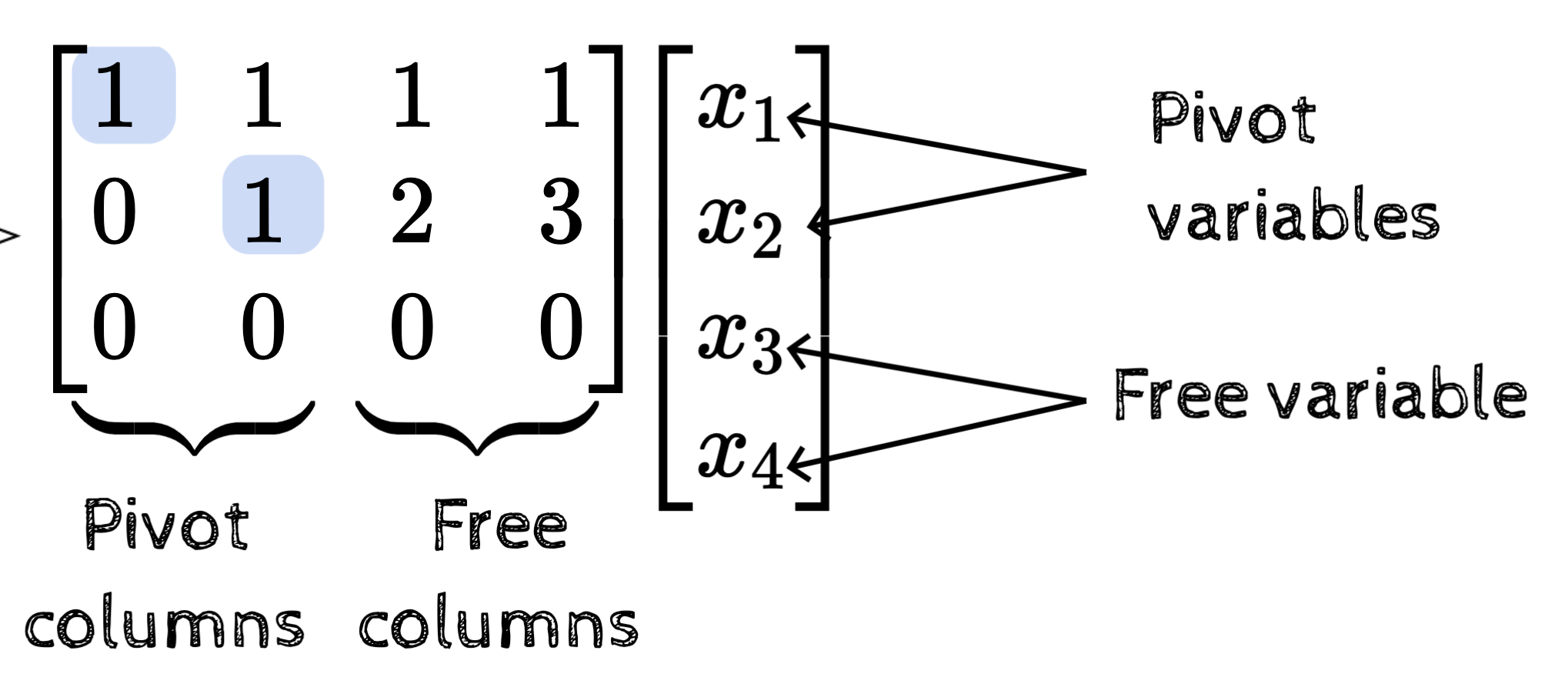
Free columns \(\implies \) non-zero nullspace \(\implies\) infinite solutions (if 1 exists)

No free columns \(\implies \) zero nullspace \(\implies\) 1 solution (if 1 exists)

1~solution
\infty~solutions
0~or~1~solution
0~or~\infty~solutions
\begin{bmatrix} ~~~&~~~&~~~\\ ~~~&~~~&~~~\\ ~~~&~~~&~~~\\ \end{bmatrix}
rank=m=n
rank=m < n
\begin{bmatrix} ~~~&~~~&~~~&~~~&~~~\\ ~~~&~~~&~~~&~~~&~~~\\ ~~~&~~~&~~~&~~~&~~~\\ \end{bmatrix}
\underbrace{~~~~~~~~~~~~~~~~~~}
\underbrace{~~~~~~~~~~~~~~~}
\begin{bmatrix} ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~& \end{bmatrix}

No Free columns

rank=n < m
\begin{bmatrix} ~~~&~~~&~~~&~~~&~~~\\ ~~~&~~~&~~~&~~~&~~~\\ ~~~&~~~&~~~&~~~&~~~\\ \end{bmatrix}

Pivot columns

\underbrace{~~~~~~~~~~~~~}
\underbrace{~~~~~~~~~~~~~~~~~~~~}

Free columns

\begin{bmatrix} ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~&\\ ~~~&~~~& \end{bmatrix}
\underbrace{~~~~~~}

Free

Pivot

\underbrace{~~~~~~~~~}

Practice Problems

For each of the above matrices, find out the number of possible solutions for Ax = b (for any b)

\begin{bmatrix} 1&2&3\\ 1&1&2\\ 2&1&0 \end{bmatrix}
\begin{bmatrix} 1&2&3&3&2&1\\ 1&2&2&1&1&2\\ 2&0&0&1&2&2 \end{bmatrix}
\begin{bmatrix} 0&2&2\\ 1&2&1\\ 2&1&3\\ 3&1&1\\ -1&1&-2\\ 2&1&0\\ \end{bmatrix}

Bonus Q: Also figure out what does the rref  look like

\begin{bmatrix} 1&2&3&3&2&1\\ 2&1&0&1&2&2\\ 4&5&6&7&6&4 \end{bmatrix}

Rank Nullity Theorem

rank(A) + nullity(A) = n
rank(A) = dimension~of~column~space~of~A
nullity(A) = dimension~of~nullspace~of~A
n = number~of~columns~of~A

https://www.math.purdue.edu/files/academic/courses/2010spring/MA26200/4-9.pdf

The mystery

Why is the number of independent rows equal to the number of independent columns? (or why does GE discover independent columns)

Outline of Proof: Enough to show that the dimension of the column space of \( A \)  is the same as the dimension of the column space of \( A^\top \)

\begin{bmatrix} 1&1&2\\ 0&1&1\\ 0&0&0\\ 0&0&0\\ \end{bmatrix}
\begin{bmatrix} 1&1&2\\ 1&2&3\\ 1&3&4\\ 1&4&5\\ \end{bmatrix}
A
\begin{bmatrix} 1&1&1&1\\ 1&2&3&4\\ 2&3&4&5 \end{bmatrix}
\begin{bmatrix} 1&1&1&1\\ 0&1&2&3\\ 0&0&0&0 \end{bmatrix}
A^\top

The mystery

Why is it enough to show this?

\begin{bmatrix} 1&1&2\\ 0&1&1\\ 0&0&0\\ 0&0&0\\ \end{bmatrix}
\begin{bmatrix} 1&1&2\\ 1&2&3\\ 1&3&4\\ 1&4&5\\ \end{bmatrix}
\begin{bmatrix} 1&1&1&1\\ 1&2&3&4\\ 2&3&4&5 \end{bmatrix}
\begin{bmatrix} 1&1&1&1\\ 0&1&2&3\\ 0&0&0&0 \end{bmatrix}
A
A^\top

Outline of Proof: Enough to show that the dimension of the column space of \( A \)  is the same as the dimension of the column space of \( A^\top \)

because we know that ... ...

number of independent columns of \(A\) = dimension of column space of \(A\)

number of independent columns of \(A^\top\) = dimension of column space of \(A^\top\)

number of independent columns of \(A^\top\) = number of independent rows of \(A\)

The mystery

Theorem: \(A^\top A\mathbf{x} = 0\) iff  \(A\mathbf{x} = 0\)

(number of indep. rows = number of indep. columns)

Proof (the if part): \(A^\top A\mathbf{x} = 0\) if  \(A\mathbf{x} = 0\)

Proof (the only if part): \(A\mathbf{x} = 0\) if  \(A^\top A\mathbf{x} = 0\)

\(A\mathbf{x} = 0\)

\(\mathcal{N}(A^\top A) = \mathcal{N}(A) \)  

Multiplying both sides by \(A^\top\) 

\(A^\top A\mathbf{x} = A^\top0 = 0\)

Multiplying both sides by \(\mathbf{x}^\top\) 

\(A^\top A\mathbf{x} = 0\)

\(\implies\)

\(\mathbf{x}^\top A^\top A\mathbf{x} = 0\)

\((A\mathbf{x})^\top A\mathbf{x} = 0\)

\(\implies\)

\(A\mathbf{x} = 0\)

The mystery

(number of indep. rows = number of indep. columns)

Previous Theorem: 

\(A\mathbf{x} = \mathbf{0}\) iff \(A^\top(A\mathbf{x}) = \mathbf{0}\) 

\( \implies  \mathcal{N}(A) = \mathcal{N}(A^\top A) \)

\( \implies  dim(\mathcal{N}(A)) = dim(\mathcal{N}(A^\top A)) \)

\( \implies  dim(\mathcal{C}(A)) = dim(\mathcal{C}(A^\top A)) \leq dim(\mathcal{C}(A^\top))\)

(rank + nullity thm.)

now replace \( A \) by \( A^\top \)

\(A^\top\mathbf{x} = \mathbf{0}\) iff \(A(A^\top\mathbf{x}) = \mathbf{0}\) 

\( \implies  \mathcal{N}(A^\top) = \mathcal{N}(A A^\top) \)

(columns of \(A^\top A\) are lin. comb. of columns of \(A^\top\) )

\( \implies  dim(\mathcal{N}(A^\top)) = dim(\mathcal{N}(AA^\top)) \)

\( \implies  dim(\mathcal{C}(A^\top)) = dim(\mathcal{C}(AA^\top)) \leq dim(\mathcal{C}(A))\)

The mystery

(number of indep. rows = number of indep. columns)

\( \therefore  dim(\mathcal{C}(A)) = dim(\mathcal{C}(A^\top)) \)

\( \therefore  rank(A) = rank(A^\top) \)

\( \therefore \) number of indep. columns of A = number of indep. columns of \( A^\top \)

\( \therefore \) number of indep. columns of A = number of indep. rows of \( A \)

Hence GE discovers independent columns while discovering independent rows!

Another mystery

The number of vectors in the basis of \( \mathbb{R}^n \) cannot be greater than \( n \)

(coming soon

..... in Quiz 1)

Hint: You can answer this based on whatever you have learnt today!

Learning Objectives

How do you find one solution for Ax=b? (if it exists)

What is the connection between rank and number of solutions?

How do you find all solutions for Ax =b?

(achieved)

A couple of unsolved mysteries!

Made with Slides.com