CS6910: Fundamentals of Deep Learning

Lecture 2: McCulloch Pitts Neuron, Thresholding Logic, Perceptrons, Perceptron Learning Algorithm and Convergence, Multilayer Perceptrons (MLPs), Representation Power of MLPs

Mitesh M. Khapra

Department of Computer Science and Engineering, IIT Madras

Learning Objectives

At the end of this lecture, student will master the basics behind McCulloch Pitts Neuron, Thresholding Logic, Perceptrons, Perceptron Learning Algorithm and Convergence, Multilayer Perceptrons (MLPs), Representation Power of MLPs

Module 2.1: Biological Neurons

The most fundamental unit of a deep neural network is called an artificial neuron

Why is it called a neuron ? Where does the inspiration come from ?

The inspiration comes from biology (more specifically, from the brain)

biological neurons = neural cells = neural processing units

We will first see what a biological neuron looks like

Artificial Neuron

$$x_1$$

$$w_1$$

$$x_2$$

$$x_3$$

$$y_1$$

$$\sigma$$

$$w_2$$

$$w_3$$

dendrite: receives signals from other neurons

synapse: point of connection to other neurons

soma: processes the information

axon: transmits the output of this neuron

Biological Neurons*

*Image adapted from

https://cdn.vectorstock.com/i/composite/12,25/neuron-cell-vector-81225.jpg

soma

dendrite

axon

synapse

Let us see a very cartoonish illustration of how a neuron works

Our sense organs interact with the outside world

They relay information to the neurons

The neurons (may) get activated and produces a response (laughter in this case)

There is a massively parallel interconnected network of neurons

Of course, in reality, it is not just a single neuron which does all this

The sense organs relay information to the lowest layer of neurons

Some of these neurons may fire (in red) in response to this information and in turn relay information to other neurons they are connected to

These neurons may also fire (again, in red) and the process continues

An average human brain has around $10^{11} $(100 billion) neurons!

eventually resulting in a response (laughter in this case)

This massively parallel network also ensures that there is division of work

Each neuron may perform a certain role or respond to a certain stimulus

This massively parallel network also ensures that there is division of work

Each neuron may perform a certain role or respond to a certain stimulus

A simplified illustration

fires if visual is funny

fires if speech style is funny

fires if text is funny

fires if at least 2 of 3 inputs fired

We illustrate this with the help of visual cortex (part of the brain) which deals with processing visual information

Starting from the retina, the information is relayed to several layers (follow the arrows)

We observe that the layers V1, V2 to AIT form a hierarchy (from identifying simple visual forms to high level objects)

The neurons in the brain are arranged in a hierarchy

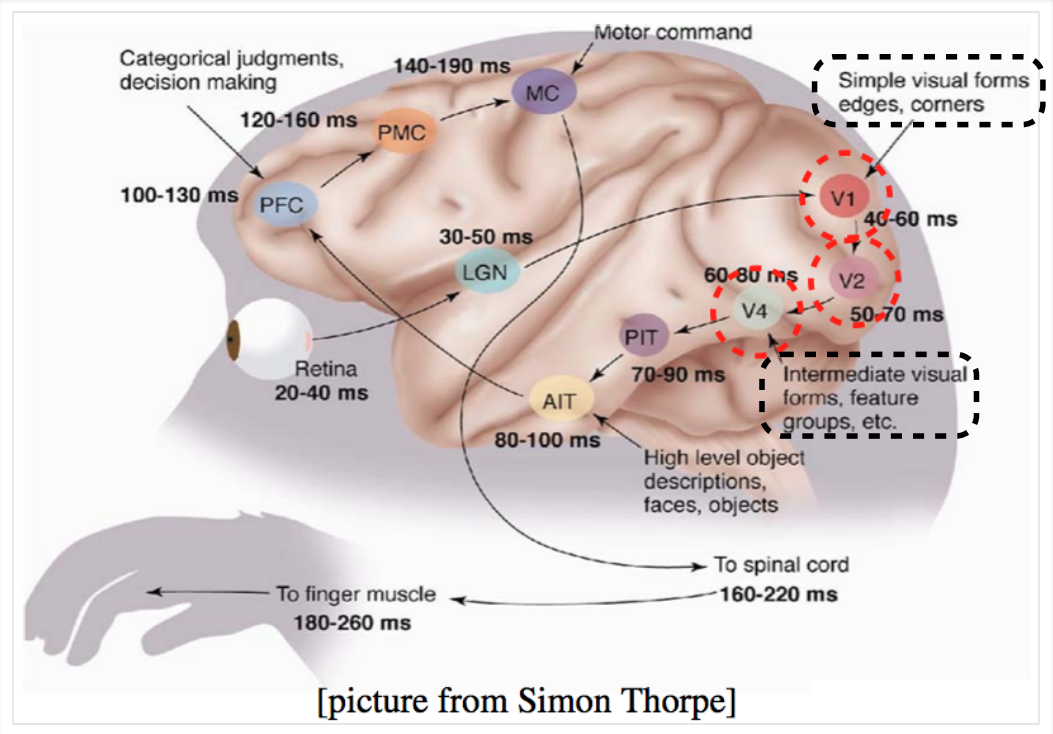
Sample illustration of hierarchical processing*

________________________________________

*Idea borrowed from Hugo Larochelle’s lecture slides

Layer 1: detect edges & corners

Layer 3: detect high level objects, faces, etc.

face

nose

mouth

eyes

Layer 2: form feature groups

Disclaimer

I understand very little about how the brain works!

What you saw so far is an overly simplified explanation of how the brain works!

But this explanation suffices for the purpose of this course!

Module 2.2: McCulloch Pitts Neuron

McCulloch (neuroscientist) and Pitts (logician) proposed a highly simplified computational model of the neuron (1943)

$y = 0$ if any $x_i$ is inhibitory, else

g(x_1,x_2,...,x_n) = g(x) = \sum_{i=1}^{n}\ x_i

$y=f(g(x)) = 1$ if $g(x) \geq \theta$

$\theta$ is called the thresholding parameter

This is the thresholding logic

$f$

$g$

$x_1$

$x_2$

$x_n$

..

$y\in \lbrace0,1\rbrace$

$g$ aggregates the inputs

The inputs can be excitatory or inhibitory

$\in \lbrace0,1\rbrace$

and the function $f$ takes a decision based on this aggregation

$= 0$ if $g(x) < \theta$

Let us implement some boolean functions using this McCulloch Pitts (MP) neuron ...

$x_1$

$\theta$

$x_2$

$y\in \lbrace0,1\rbrace$

$x_3$

A McCulloch Pitts unit

* circle at the end indicates inhibitory input: if any inhibitory input is 1 the output will be 0

AND function

$y\in \lbrace0,1\rbrace$

$x_1$

$x_2$

$x_3$

$x_1$

$x_2$

$y\in \lbrace0,1\rbrace$

$x_3$

OR function

$x_1$ AND !$x_2$*

$x_1$

$x_2$

$y\in \lbrace0,1\rbrace$

NOR function

$x_1$

$x_2$

$y\in \lbrace0,1\rbrace$

NOT function

$x_1$

$y\in \lbrace0,1\rbrace$

Can any boolean function be represented using a McCulloch Pitts unit?

Before answering this question let us first see the geometric interpretation of a MP unit...

A single MP neuron splits the input points (4 points for 2 binary inputs) into two halves

Points lying on or above the line $\sum_{i=1}^{n}\ x_i-\theta=0$ and points lying below this line

In other words, all inputs which produce an output 0 will be on one side $(\sum_{i=1}^{n}\ x_i<\theta$) of the line and all inputs which produce an output 1 will lie on the other side $(\sum_{i=1}^{n}\ x_i\geq \theta$) of this line

Let us convince ourselves about this with a few more examples (if it is not already clear from the math)

$y\in \lbrace0,1\rbrace$

$x_1$

$x_2$

OR function

x_1 + x_2 = \sum_{i=1}^{2}\ x_i \geq 1

$x_1$

$x_2$

$y\in \lbrace0,1\rbrace$

AND function

x_1 + x_2 = \sum_{i=1}^{2}\ x_i \geq 2

$x_1$

$x_2$

$y\in \lbrace0,1\rbrace$

Tautology (always ON)

What if we have more than 2 inputs?

Well, instead of a line we will have a plane

For the OR function, we want a plane such that the point (0,0,0) lies on one side and the remaining 7 points lie on the other side of the plane

$x_1$

$x_2$

$y\in \lbrace0,1\rbrace$

$x_3$

$x_1 + x_2 + x_3= \theta = 1$

The story so far ...

A single McCulloch Pitts Neuron can be used to represent boolean functions which are linearly separable

Linear separability (for boolean functions) : There exists a line (plane) such that all inputs which produce a 1 lie on one side of the line (plane) and all inputs which produce a 0 lie on other side of the line (plane)

Module 2.3: Perceptron

The story ahead ...

What about non-boolean (say, real) inputs ?

Do we always need to hand code the threshold ?

Are all inputs equal ? What if we want to assign more weight (importance) to some inputs ?

What about functions which are not linearly separable ?

Frank Rosenblatt, an American psychologist, proposed the classical perceptron model (1958)

Refined and carefully analyzed by Minsky and Papert (1969) - their model is referred to as the perceptron model here

A more general computational model than McCulloch–Pitts neurons

Main differences: Introduction of numerical weights for inputs and a mechanism for learning these weights

Inputs are no longer limited to boolean values

$$x_1$$

$$x_2$$

$$x_n$$

$$y$$

$$w_1$$

$$w_2$$

$$w_n$$

$$..$$

if \displaystyle\sum_{\textcolor{red}{i=1}}^n \ w_i*x_i \geq \theta

if \displaystyle\sum_{\textcolor{red}{i=1}}^n \ w_i*x_i < \theta

y = 1

= 0

Rewriting the above,

if \displaystyle\sum_{\textcolor{red}{i=1}}^n \ w_i*x_i - \theta \geq 0

if \displaystyle\sum_{\textcolor{red}{i=1}}^n \ w_i*x_i - \theta < 0

y = 1

= 0

A more accepted convention,

if \displaystyle\sum_{\textcolor{red}{i=0}}^n \ w_i*x_i \geq 0

if \displaystyle\sum_{\textcolor{red}{i=0}}^n \ w_i*x_i < 0

y = 1

= 0

where, $x_0 = 1$ and $w_0 = -\theta$

$$x_0=1$$

$$w_0=-\theta$$

$$x_1$$

$$w_1$$

$$x_2$$

$$x_n$$

$$w_2$$

$$w_n$$

$$..$$

$$y$$

We will now try to answer the following questions:

Why are we trying to implement boolean functions?

Why do we need weights ?

Why is $w_0 = -\theta$ called the bias ?

x1 = isActorDamon

x2 = isGenreThriller

x3 = isDirectorNolan

Consider the task of predicting whether we would like a movie or not

Suppose, we base our decision on 3 inputs (binary, for simplicity)

Based on our past viewing experience (data), we may give a high weight to isDirectorNolan as compared to the other inputs

Specifically, even if the actor is not Matt Damon and the genre is not thriller we would still want to cross the threshold $\theta$ by assigning a high weight to isDirectorNolan

$$x_1$$

$$w_1$$

$$x_2$$

$$y$$

$$w_2$$

$$w_3$$

$$x_0=1$$

$$w_0=-\theta$$

$$x_3$$

$$x_1$$

$$w_1$$

$$x_2$$

$$y$$

$$w_2$$

$$w_3$$

$$x_0=1$$

$$w_0=-\theta$$

$$x_3$$

x1 = isActorDamon

x2 = isGenreThriller

x3 = isDirectorNolan

$w_0$ is called the bias as it represents the prior (prejudice)

A movie buff may have a very low threshold and may watch any movie irrespective of the genre, actor, director $[\theta=0]$

On the other hand, a selective viewer may only watch thrillers starring Matt Damon and directed by Nolan $[\theta=3]$

The weights $(w_1, w_2, ..., w_n)$ and the the bias $(w_0)$ will depend on the data (viewer history in this case)

What kind of functions can be implemented using the perceptron? Any difference from McCulloch Pitts neurons?

All inputs which produce a 1 lie on one side and all inputs which produce a 0 lie on the other side

In other words, a single perceptron can only be used to implement linearly separable functions

Then what is the difference?

We will first revisit some boolean functions and then see the perceptron learning algorithm (for learning weights)

McCulloch Pitts Neuron

(assuming no inhibitory inputs)

if \displaystyle\sum_{i=0}^n \ x_i \geq 0

if \displaystyle\sum_{i=0}^n \ x_i < 0

y = 1

= 0

if \displaystyle\sum_{i=0}^n \ \textcolor{red}{w_i}*x_i \geq 0

if \displaystyle\sum_{i=0}^n \ \textcolor{red}{w_i} * x_i < 0

y = 1

= 0

Perceptron

From the equations it should be clear that even a perceptron separates the input space into two halves

The weights (including threshold) can be learned and the inputs can be real valued

$x_1$

$x_2$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

w_0 + \sum_{i=1}^{2}\ w_ix_i < 0

w_0 + \sum_{i=1}^{2}\ w_ix_i \geq 0

w_0 + w_1 . 0 + w_2 . 0 < 0 \implies w_0 < 0

w_0 + w_1 . 0 + w_2 . 1 \geq 0 \implies w_2 \geq -w_0

w_0 + w_1 . 1 + w_2 . 0 \geq 0 \implies w_1 \geq -w_0

w_0 + w_1 . 1 + w_2 . 1 \geq 0 \implies w_1 + w_2 \geq -w_0

One possible solution to this set of inequalities is $w_0 = 1$, $w_1 = 1.1$,$w_2 = 1.1$ (and various other solutions are possible)

Note that we can come up with a similar set of inequalities and find the value of $\theta$ for a McCulloch Pitts neuron also (Try it!)

Module 2.4: Errors and Error Surfaces

Let us fix the threshold ($-w_0 = 1$) and try different values of $w_1$, $w_2$

Say, $w_1 = -1$, $w_2 = -1$

What is wrong with this line?

Lets try some more values of $w_1$, $w_2$ and note how many errors we make

We are interested in those values of $w_0$, $w_1$,$ w_2$ which result in 0 error

Let us plot the error surface corresponding to different values of $w_0$, $w_1$, $ w_2$

We make an error on 1 out of the 4 inputs

$w_1$

$w_2$

errors

$-1$

$3$

$1.5$

$0$

$1$

$0.45$

$3$

For ease of analysis, we will keep $w_0$ fixed (-1) and plot the error for different values of $w_1$, $w_2$

For a given $w_0$, $w_1$, $w_2$ we will compute $-w_0+w_1x_1+w_2x_2$ for all comb-inations of ($x_1,x_2$) and note down how many errors we make

For the OR function, an error occurs if ($x_1,x_2$) = ($0,0$) but $-w_0+w_1x_1+w_2x_2 \geq 0$ or if ($x_1,x_2$) $\neq$ ($0,0$) but $-w_0+w_1x_1+w_2x_2 < 0$

We are interested in finding an algorithm which finds the values of $w_1$, $w_2$ which minimize this error

Module 2.5: Perceptron Learning Algorithm

We will now see a more principled approach for learning these weights and threshold but before that let us answer this question...

Apart from implementing boolean functions (which does not look very interesting) what can a perceptron be used for ?

Our interest lies in the use of perceptron as a binary classifier. Let us see what this means...

Let us reconsider our problem of deciding whether to watch a movie or not

Suppose we are given a list of m movies and a label (class) associated with each movie indicating whether the user liked this movie or not : binary decision

Further, suppose we represent each movie with $n$ features (some boolean, some real valued)

We will assume that the data is linearly separable and we want a perceptron to learn how to make this decision

In other words, we want the perceptron to find the equation of this separating plane (or find the values of $w_0,w_1,w_2,...,w_m$)

x1 = isActorDamon

x2 = isGenreThriller

x3 = isDirectorNolan

...

x4 = imdbRating

(scaled to 0 to 1)

xn = criticsRating

(scaled to 0 to 1)

$$w_1$$

$$w_2$$

$$w_n$$

$$..$$

$$w_0=-\theta$$

$$x_1$$

$$x_2$$

$$x_n$$

$$y$$

$$..$$

$$x_0=1$$

Why would this work ?

To understand why this works we will have to get into a bit of Linear Algebra and a bit of geometry...

$P \gets$ $inputs$ $with$ $label$ $1$;

$N \gets$ $inputs$ $with$ $label$ $0$;

Initialize $\text w$ randomly;

while $!convergence$ do

Pick random $\text x$ $\isin$ $ P$ $\cup$ $ N$ ;

$\text w$ = $\text w$ $+$ $\text x$ ;

end

end

//the algorithm converges when all the inputs
are classified correctly

if $\text x$ $\isin$ $\text P$ $and$ $\sum_{i=0}^{n}\ w_i*x_i < 0$ then

end

if $\text x$ $\isin$ $\text N$ $and$ $\sum_{i=0}^{n}\ w_i*x_i \geq 0$ then

$\text w$ = $\text w$ $-$ $\text x$ ;

Algorithm: Perceptron Learning Algorithm

We are interested in finding the line $\text w^\text T \text x=0$ which divides the input space into two halves

Every point ($\text x$) on this line satisfies the equation $\text w^\text T \text x=0$

What can you tell about the angle ($\alpha$) between $\text w$ and any point ($\text x$) which lies on this line ?

Since the vector $\text w$ is perpendicular to every point on the line it is actually perpendicular to the line itself

The angle is $90^\circ$

($\because$ $cos \alpha $= ${w^Tx\over \parallel w \parallel \parallel x \parallel}$ = $0$)

Consider two vectors $\text w$ and $\text x$

$\text w$ $=[w_0,w_1,w_2,...,w_n]$

$\text x$ $=[1,x_1,x_2,...,x_n]$

$\text w \sdot \text x = \text w^\text T \text x = \displaystyle\sum_{i=0}^n \ w_i * x_i$

We can thus rewrite the perceptron rule as

$y = 1$ $if \text w^\text T \text x \geq 0$

$ = 0$ $if \text w^\text T \text x < 0$

Consider some points (vectors) which lie in the positive half space of this line (i.e., $\text w^\text T \text x=0$)

What will be the angle between any such vector and $\text w$ ?

What about points (vectors) which lie in the negative half space of this line (i.e., $\text w^\text T \text x<0$)

What will be the angle between any such vector and $\text w$ ?

Of course, this also follows from the formula

($cos \alpha $= ${w^Tx\over \parallel w \parallel \parallel x \parallel}$)

Keeping this picture in mind let us revisit the algorithm

$x_2$

$x_1$

$p_2$

$p_3$

$\text w$

$p_1$

$n_1$

$n_2$

$n_3$

Obviously, less than $90^\circ$

Obviously, greater than $90^\circ$

\text w ^ \text T \text x = 0

Algorithm: Perceptron Learning Algorithm

$P \gets$ $inputs$ $with$ $label$ $1$;

$N \gets$ $inputs$ $with$ $label$ $0$;

Initialize $\text w$ randomly;

while $!convergence$ do

Pick random $\text x$ $\isin$ $ P$ $\cup$ $ N$ ;

$\text w$ = $\text w$ $+$ $\text x$ ;

end

end

//the algorithm converges when all the inputs
are classified correctly

if $\text x$ $\isin$ $\text P$ $and$ $\sum_{i=0}^{n}\ w_i*x_i < 0$ then

end

if $\text x$ $\isin$ $\text N$ $and$ $\sum_{i=0}^{n}\ w_i*x_i \geq 0$ then

$\text w$ = $\text w$ $-$ $\text x$ ;

For $\text x$ $\isin$ $ P$ if $\text w^\text T \text x < 0$ then it means that the angle ($\alpha$) between this $\text x$ and the current $\text w$ is greater than $90^\circ$

What happens to the new angle ($\alpha_{new}$) when $\text w_{\text {new}} = \text w + \text x$

$cos$($\alpha_{new}$) $\varpropto$ ($\text w_{\text {new}})^\text T + \text x$

$\varpropto (\text w+\text x)^\text T \text x$

$\varpropto \text w^\text T \text x + \text x^\text T \text x$

$\varpropto cos \alpha + \text x^\text T \text x$

$cos$($\alpha_{new}$) $> cos \alpha$

Thus $\alpha_{new}$ will be less than $\alpha$ and this is exactly what we want

($cos \alpha $= ${w^Tx\over \parallel w \parallel \parallel x \parallel}$)

(but we want to be less than $90^\circ$)

Algorithm: Perceptron Learning Algorithm

$P \gets$ $inputs$ $with$ $label$ $1$;

$N \gets$ $inputs$ $with$ $label$ $0$;

Initialize $\text w$ randomly;

while $!convergence$ do

Pick random $\text x$ $\isin$ $ P$ $\cup$ $ N$ ;

$\text w$ = $\text w$ $+$ $\text x$ ;

end

end

//the algorithm converges when all the inputs
are classified correctly

if $\text x$ $\isin$ $\text P$ $and$ $\sum_{i=0}^{n}\ w_i*x_i < 0$ then

end

if $\text x$ $\isin$ $\text N$ $and$ $\sum_{i=0}^{n}\ w_i*x_i \geq 0$ then

$\text w$ = $\text w$ $-$ $\text x$ ;

For $\text x$ $\isin$ $ N$ if $\text w^\text T \text x \geq 0$ then it means that the angle ($\alpha$) between this $\text x$ and the current $\text w$ is less than $90^\circ$

What happens to the new angle ($\alpha_{new}$) when $\text w_{\text {new}} = \text w - \text x$

$cos$($\alpha_{new}$) $\varpropto$ ($\text w_{\text {new}})^\text T + \text x$

$\varpropto (\text w-\text x)^\text T \text x$

$\varpropto \text w^\text T \text x - \text x^\text T \text x$

$\varpropto cos \alpha - \text x^\text T \text x$

$cos$($\alpha_{new}$) $< cos \alpha$

Thus $\alpha_{new}$ will be greater than $\alpha$ and this is exactly what we want

($cos \alpha $= ${w^Tx\over \parallel w \parallel \parallel x \parallel}$)

(but we want to be greater than $90^\circ$)

We will now see this algorithm in action for a toy dataset

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $p_1$), apply correction $\text w = \text w + \text x$ ($\because$ $\text w \sdot \text x < 0$) (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $p_2$), apply correction $\text w = \text w + \text x$ ($\because$ $\text w \sdot \text x < 0$) (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $n_1$), apply correction $\text w = \text w - \text x$ ($\because$ $\text w \sdot \text x \geq 0$) (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $n_3$), no correction
needed $\because\ \text w \sdot \text x < 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $n_2$), no correction
needed $\because\ \text w \sdot \text x < 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $p_3$), apply correction $\text w = \text w + \text x$ ($\because$ $\text w \sdot \text x < 0$) (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $p_1$), no correction
needed $\because\ \text w \sdot \text x \geq 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $p_2$), no correction
needed $\because\ \text w \sdot \text x \geq 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $n_1$), no correction
needed $\because\ \text w \sdot \text x < 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $n_3$), no correction
needed $\because\ \text w \sdot \text x < 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $n_2$), no correction
needed $\because\ \text w \sdot \text x < 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

Randomly pick a point (say, $p_3$), no correction
needed $\because\ \text w \sdot \text x \geq 0$ (you can check the angle visually)

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

We initialized $\text w$ to a random value

We observe that currently, $\text w \sdot \text x < 0$ ($\because$ angle $\alpha > 90^\circ$ for all the positive points and $\text w \sdot \text x \geq 0$ ($\because$ angle $\alpha < 90^\circ$ for all the negative points (the situation is exactly opposite of what we actually want it to be)

We now run the algorithm by randomly going over the points

The algorithm has converged

$x_2$

$x_1$

$p_2$

$p_3$

$p_1$

$n_1$

$n_2$

$n_3$

Module 2.6: Proof of Convergence

Now that we have some faith and intuition about why the algorithm works, we will see a more formal proof of convergence ...

Theorem

Definition: Two sets $P$ and $N$ of points in an $n$-dimensional space are called absolutely linearly separable if $n+1$ real numbers $w_0,w_1,...,w_n$ exist such that every point ($x_1,x_2,...,x_n)\in P$ satisfies $\sum_{i=1}^{n}\ w_ix_i > 0$ and every point $(x_1,x_2,...,x_n) \in N$ satisfies $\sum_{i=1}^{n}\ w_ix_i < w_0$.

Proposition: If the sets $P$ and $N$ are finite and linearly separable, the perceptron learning algorithm updates the weight vector $w_t$ a finite number of times. In other words: if the vectors in $P$ and $N$ are tested cyclically one after the other, a weight vector $w_t$ is found after a finite number of steps $t$ which can separate the two sets.

Proof: On the next slide

$n+1$ real numbers $w_0,w_1,...,w_n$ exist such that every point ($x_1,x_2,...,x_n)\in P$ satisfies $\sum_{i=1}^{n}\ w_ix_i > 0$ and every point $(x_1,x_2,...,x_n) \in N$ satisfies $\sum_{i=1}^{n}\ w_ix_i < w_0$.

such that every point ($x_1,x_2,...,x_n)\in P$ satisfies $\sum_{i=1}^{n}\ w_ix_i > 0$ and every point $(x_1,x_2,...,x_n) \in N$ satisfies $\sum_{i=1}^{n}\ w_ix_i < w_0$.

and every point $(x_1,x_2,...,x_n) \in N$ satisfies $\sum_{i=1}^{n}\ w_i*x_i < w_0$.

the perceptron learning algorithm updates the weight vector $w_t$ a finite number of times. In other words: if the vectors in $P$ and $N$ are tested cyclically one after the other, a weight vector $w_t$ is found after a finite number of steps $t$ which can separate the two sets.

In other words: if the vectors in $P$ and $N$ are tested cyclically one after the other, a weight vector $w_t$ is found after a finite number of steps $t$ which can separate the two sets.

a weight vector $w_t$ is found after a finite number of steps $t$ which can separate the two sets.

$N \gets$ $inputs$ $with$ $label$ $0$;

Initialize $\text w$ randomly;

while $!convergence$ do

Pick random $\text p$ $\isin$ $ P'$

$\text w$ = $\text w$ $+$ $\text x$ ;

end

end

//the algorithm converges when all the inputs are classified correctly

if $\text x$ $\isin$ $\text P$ $and$ $\sum_{i=0}^{n}\ w_i*x_i < 0$ then

$N^-$ contains negations of all points in $N$;

$P' \gets P \cup N$

$p \gets$ ${p \over \parallel p \parallel}$ (so now, $\parallel p\parallel = 1)$

Setup

If $\text x \in N$ then $-x \in P$ ($\because w^T x < 0 \Longrightarrow w^T (-x) \geq 0$)

//notice that we do not need the other if condition

because by construction we want all points in $P'$ to lie

We can thus consider a single set $P' = P \cup N^-$ and for every element $p \in P'$ ensure that $w^Tp \geq 0$

Further we will normalize all the $p'$s so that $\parallel p \parallel = 1$ (notice that this does not affect the solution $\because if$ $w^T{p \over \parallel p \parallel} \geq 0$ then $w^Tp \geq 0$

Let $w*$ be the normalized solution vector (we know one exists as the data is linearly separable)

Algorithm: Perceptron Learning Algorithm

$P \gets$ $inputs$ $with$ $label$ $1$;

Proof:

Observations:

Now suppose at time step $t$ we inspected the point pi and found that $w^T \sdot p_i \leq 0$

We make a correction $w_{t+1} = w_t + p_i$

Let $\beta$ be the angle between $w^*$ and $w_{t+1}$

$cos \beta = $${w^* \sdot w_{t+1} \over \parallel w_{t+1} \parallel}$

$Numerator =$ $w^* \sdot w_{t+1} = w^* \sdot (w_t+p_i)$

$=w^* \sdot w_t + w^* \sdot p_i$

$\geq w^* \sdot (w_{t-1} +p_j) + \delta$

$\geq w^* \sdot w_{t-1} + w^* \sdot p_j + \delta$

$\geq w^* \sdot w_{t-1} + 2\delta$

$\geq w^* \sdot w_0 + (k)\delta$ (By induction)

$w^*$ is some optimal solution which exists but we don’t know what it is

We do not make a correction at every time-step

We make a correction only if $w^T \sdot p_i \leq 0$ at that time step

So at time-step $t$ we would have made only $k(\leq t)$ corrections

Every time we make a correction a quantity $\delta$ gets added to the numerator

So by time-step $t$, a quantity $k\delta $ gets added to the numerator

$\geq w^* \sdot w_t + \delta$

($\delta=min$ {$w^* \sdot p_i | \forall i$})

Proof (continued):

So far we have, $w^T \sdot p_i \leq 0$ (and hence we made the correction)

$cos \beta = $${w^* \sdot w_{t+1} \over \parallel w_{t+1} \parallel}$ (by definition)

$Numerator =$ $\geq w^* \sdot w_0 + (k)\delta$ (proved by induction)

$=(w_t+p_i) \sdot (w_t+p_i)$

$=\parallel w_t \parallel ^2 + 2w_t \sdot p_i + \parallel p_i \parallel ^2 $

$\leq \parallel w_t \parallel ^2 + \parallel p_i \parallel ^2 $

($\because w_t \sdot p_i \leq 0$)

$Denominator ^2= \parallel w_{t+1} \parallel ^2$

($\because \parallel p_i \parallel ^2 = 1$)

$\leq \parallel w_t \parallel ^2 + 1 $

$\leq (\parallel w_{t-1} \parallel ^2 + 1)+1$

$\leq \parallel w_{t-1} \parallel ^2 + 2$

$\leq \parallel w_0 \parallel ^2 + (k)$ (By same observation that we made about $\delta$)

Proof (continued):

So far we have, $w^T \sdot p_i \leq 0$ (and hence we made the correction)

$cos \beta = $${w^* \sdot w_{t+1} \over \parallel w_{t+1} \parallel}$ (by definition)

$Numerator $ $\geq w^* \sdot w_0 + (k)\delta$ (proved by induction)

$Denominator ^2 $ $\leq \parallel w_0 \parallel ^2 + (k)$ (By same observation that we made about $\delta$)

$cos \beta = $${w^* \sdot w_0 + k \delta \over \sqrt {{\parallel w_0 \parallel}^2 + k}}$ (by definition)

$cos \beta$ thus grows proportional to $\sqrt k$

As $k$ (number of corrections) increases $cos \beta$ can become arbitrarily large

But since $cos \beta \leq 1$, $k$ must be bounded by a maximum number

Thus, there can only be a finite number of corrections $(k)$ to $w$ and the algorithm will converge!

Coming back to our questions

What about non-boolean (say, real) inputs?

Do we always need to hand code the threshold?

What about functions which are not linearly separable ? Not possible with a single perceptron but we will see how to handle this ..

Real valued inputs are allowed in perceptron

No, we can learn the threshold

Are all inputs equal? What if we want to assign more weight (importance) to some inputs?

A perceptron allows weights to be assigned to inputs

Not possible with a single perceptron but we will see how to handle this ..

Module 2.7: Linearly Separable Boolean Function

So what do we do about functions which are not linearly separable ?

Let us see one such simple boolean function first ?

$x_1$

$x_2$

XOR

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

w_0 + \sum_{i=1}^{2}\ w_ix_i < 0

w_0 + \sum_{i=1}^{2}\ w_ix_i \geq 0

w_0 + \sum_{i=1}^{2}\ w_ix_i < 0

w_0 + w_1 . 0 + w_2 . 0 < 0 \implies w_0 < 0

w_0 + w_1 . 0 + w_2 . 1 \geq 0 \implies w_2 \geq -w_0

w_0 + w_1 . 1 + w_2 . 0 \geq 0 \implies w_1 \geq -w_0

w_0 + w_1 . 1 + w_2 . 1 < 0 \implies w_1 + w_2 < -w_0

The fourth condition contradicts conditions 2 and 3

And indeed you can see that it is impossible to draw a line which separates the red points from the blue points

Hence we cannot have a solution to this set of inequalities

Most real world data is not linearly separable and will always contain some outliers

While a single perceptron cannot deal with such data, we will show that a network of perceptrons can indeed deal with such data

In fact, sometimes there may not be any outliers but still the data may not be linearly separable

We need computational units (models) which can deal with such data

Before seeing how a network of perceptrons can deal with linearly inseparable data, we will discuss boolean functions in some more detail ...

How many boolean functions can you design from 2 inputs ?

Let us begin with some easy ones which you already know ..

Of these, how many are linearly separable ? (turns out all except XOR and !XOR - feel free to verify)

In general, how many boolean functions can you have for $n$ inputs ?

How many of these $2^{2^n}$ functions are not linearly separable ? For the time being, it suffices to know that at least some of these may not be linearly inseparable (I encourage you to figure out the exact answer :-))

$x_1$

$x_2$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$1$

$0$

$f_1$

$f_2$

$f_3$

$f_4$

$f_5$

$f_6$

$f_7$

$f_8$

$f_9$

$f_{10}$

$f_{11}$

$f_{12}$

$f_{13}$

$f_{14}$

$f_{15}$

$f_{16}$

(turns out all except XOR and !XOR - feel free to verify)

$2^{2^n}$

For the time being, it suffices to know that at least some of these may not be linearly inseparable (I encourage you to figure out the exact answer :-))

Module 2.8: Representation Power of a Network of Perceptrons

We will now see how to implement any boolean function using a network of perceptrons ...

$$x_1$$

$$x_2$$

$$y$$

For this discussion, we will assume True = +1
and False = -1

We consider 2 inputs and 4 perceptrons

Each input is connected to all the 4 perceptrons with specific weights

The bias ($w_0$) of each perceptron is $-2$ (i.e., each perceptron will fire only if the weighted sum of its input is $\geq 2$)

Each of these perceptrons is connected to an output perceptron by weights (which need to be learned)

The output of this perceptron ($y$) is the output
of this network

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$x_1$$

$$x_2$$

$$y$$

Terminology:

This network contains 3 layers

The layer containing the inputs ($x_1,x_2$) is called the input layer

The middle layer containing the 4 perceptrons is called the hidden layer

The final layer containing one output neuron is called the output layer

The red and blue edges are called layer 1 weights

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

$$bias=-2$$

The outputs of the 4 perceptrons in the hidden layer are denoted by $h_1,h_2,h_3,h_4$

$w_1,w_2,w_3,w_4$ are called layer 2 weights

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

We claim that this network can be used to implement any boolean function (linearly separable or not) !

In other words, we can find $w_1,w_2,w_3,w_4$ such that the truth table of any boolean function can be represented by this network

Each perceptron in the middle layer fires only for a specific input (and no two perceptrons fire for the same input)

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

Astonishing claim! Well, not really, if you understand what is going on

Well, not really, if you understand what is going on

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

the first perceptron fires for {-1,-1}

-1,-1

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

We claim that this network can be used to implement any boolean function (linearly separable or not) !

In other words, we can find $w_1,w_2,w_3,w_4$ such that the truth table of any boolean function can be represented by this network

Each perceptron in the middle layer fires only for a specific input (and no two perceptrons fire for the same input)

Astonishing claim! Well, not really, if you understand what is going on

Well, not really, if you understand what is going on

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

the second perceptron fires for {-1,1}

-1,-1

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

We claim that this network can be used to implement any boolean function (linearly separable or not) !

In other words, we can find $w_1,w_2,w_3,w_4$ such that the truth table of any boolean function can be represented by this network

Each perceptron in the middle layer fires only for a specific input (and no two perceptrons fire for the same input)

Astonishing claim! Well, not really, if you understand what is going on

Well, not really, if you understand what is going on

-1,1

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

the third perceptron fires for {1,-1}

-1,-1

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

We claim that this network can be used to implement any boolean function (linearly separable or not) !

In other words, we can find $w_1,w_2,w_3,w_4$ such that the truth table of any boolean function can be represented by this network

Each perceptron in the middle layer fires only for a specific input (and no two perceptrons fire for the same input)

Astonishing claim! Well, not really, if you understand what is going on

Well, not really, if you understand what is going on

-1,1

1,-1

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

the fourth perceptron fires for {1,1}

-1,-1

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

We claim that this network can be used to implement any boolean function (linearly separable or not) !

In other words, we can find $w_1,w_2,w_3,w_4$ such that the truth table of any boolean function can be represented by this network

Each perceptron in the middle layer fires only for a specific input (and no two perceptrons fire for the same input)

Astonishing claim! Well, not really, if you understand what is going on

Well, not really, if you understand what is going on

-1,1

1,-1

1,1

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

-1,-1

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

-1,1

1,-1

1,1

Let us see why this network works by taking an example of the XOR function

We claim that this network can be used to implement any boolean function (linearly separable or not) !

In other words, we can find $w_1,w_2,w_3,w_4$ such that the truth table of any boolean function can be represented by this network

Each perceptron in the middle layer fires only for a specific input (and no two perceptrons fire for the same input)

Astonishing claim! Well, not really, if you understand what is going on

Well, not really, if you understand what is going on

Let $w_0$ be the bias output of the neuron (i.e.,
it will fire if $\sum_{i=1}^{4}\ w_ih_i\geq w_0$

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

This results in the following four conditions to implement XOR: $w_1<w_0$, $w_2 \geq w_0$, $w_3 \geq w_0$, $w_4 < w_0$

Unlike before, there are no contradictions now and the system of inequalities can be satisfied

Essentially each $w_i$ is now responsible for one of the 4 possible inputs and can be adjusted to get the desired output for that input

-1,-1

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

-1,1

1,-1

1,1

$x_1$

$x_2$

$XOR$

$0$

$x_1$

$x_2$

$1$

$0$

$h_1$

$h_2$

$0$

$h_3$

$h_4$

$\sum_{i=1}^{4}\ w_ih_i$

$$w_1$$

$1$

$0$

$1$

$0$

$1$

$0$

$$w_2$$

$0$

$1$

$0$

$1$

$0$

$$w_3$$

$1$

$0$

$1$

$$w_4$$

It should be clear that the same network can be used to represent the remaining 15 boolean functions also

red edge indicates $w$ = -1

blue edge indicates $w$ = +1

Each boolean function will result in a different set of non-contradicting inequalities which can be satisfied by appropriately setting $w_1,w_2,w_3,w_4$

Try it!

-1,-1

$$x_1$$

$$x_2$$

$$y$$

$$bias=-2$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$h_1$$

$$h_2$$

$$h_3$$

$$h_4$$

-1,1

1,-1

1,1

What if we have more than 3 inputs ?

Again each of the 8 perceptorns will fire only for one of the 8 inputs

Each of the 8 weights in the second layer is responsible for one of the 8 inputs and can be adjusted to produce the desired output for that input

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$x_2$$

$$x_1$$

$$y$$

$$w_5$$

$$w_6$$

$$w_7$$

$$w_8$$

$$bias=-3$$

What if we have more than $n$ inputs ?

Theorem

Any boolean function of $n$ inputs can be represented exactly by a network of perceptrons containing 1 hidden layer with $2^n$ perceptrons and one output layer containing 1 perceptron

Proof (informal:) We just saw how to construct such a network

Note: A network of $2^n + 1$ perceptrons is not necessary but sufficient. For example, we already saw how to represent AND function with just 1 perceptron

Catch: As $n$ increases the number of perceptrons in the hidden layers obviously increases exponentially

Again, why do we care about boolean functions ?

How does this help us with our original problem: which was to predict whether we like a movie or not? Let us see!

Let us see!

We are given this data about our past movie experience

For each movie, we are given the values of the various factors ($x_1,x_2,...,x_n$) that we base our decision on and we are also also given the value of $y$ (like/dislike)

$p_i's$ are the points for which the output was 1 and $n_i's$ are the points for which it was $0$

The data may or may not be linearly separable

The proof that we just saw tells us that it is possible to have a network of perceptrons and learn the weights in this network such that for any given $p_i$ or $n_j$ the output of the network will be the same as $y_i$ or $y_j$ (i.e., we can separate the positive and the negative points)

\begin{bmatrix} x_{11} & x_{12} & ... & x_{1n} & y_1=1\\ x_{21} & x_{22} & ... & x_{2n} & y_2=1\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ x_{k1} & x_{k2} & ... & x_{kn} & y_i=0\\ x_{j1} & x_{j2} & ... & x_{jn} & y_j=0\\ \vdots & \vdots & \vdots & \vdots & \vdots\\ \end{bmatrix}

\begin{matrix} p_1\\ p_2\\ \vdots\\ n_1\\ n_2\\ \vdots\\ \end{matrix}

$$y$$

$$w_1$$

$$w_2$$

$$w_3$$

$$w_4$$

$$w_5$$

$$w_6$$

$$w_7$$

$$w_8$$

$$bias=-3$$

$$x_1$$

$$x_2$$

$$x_3$$

CS6910: Fundamentals of Deep Learning

Lecture 2: McCulloch Pitts Neuron, Thresholding Logic, Perceptrons, Perceptron Learning Algorithm and Convergence, Multilayer Perceptrons (MLPs), Representation Power of MLPs

Mitesh M. Khapra

Learning Objectives

At the end of this lecture, student will master the basics behind McCulloch Pitts Neuron, Thresholding Logic, Perceptrons, Perceptron Learning Algorithm and Convergence, Multilayer Perceptrons (MLPs), Representation Power of MLPs

Module 2.1: Biological Neurons

The most fundamental unit of a deep neural network is called an artificial neuron

Why is it called a neuron ? Where does the inspiration come from ?

The inspiration comes from biology (more specifically, from the brain)

biological neurons = neural cells = neural processing units

We will first see what a biological neuron looks like

dendrite: receives signals from other neurons

synapse: point of connection to other neurons

soma: processes the information

axon: transmits the output of this neuron

Biological Neurons*

*Image adapted from

Let us see a very cartoonish illustration of how a neuron works

Our sense organs interact with the outside world

They relay information to the neurons

The neurons (may) get activated and produces a response (laughter in this case)

There is a massively parallel interconnected network of neurons

Of course, in reality, it is not just a single neuron which does all this

The sense organs relay information to the lowest layer of neurons

Some of these neurons may fire (in red) in response to this information and in turn relay information to other neurons they are connected to

These neurons may also fire (again, in red) and the process continues

An average human brain has around \(10^{11} \)(100 billion) neurons!

eventually resulting in a response (laughter in this case)

This massively parallel network also ensures that there is division of work

Each neuron may perform a certain role or respond to a certain stimulus

This massively parallel network also ensures that there is division of work

Each neuron may perform a certain role or respond to a certain stimulus

A simplified illustration

We illustrate this with the help of visual cortex (part of the brain) which deals with processing visual information

Starting from the retina, the information is relayed to several layers (follow the arrows)

We observe that the layers V1, V2 to AIT form a hierarchy (from identifying simple visual forms to high level objects)

The neurons in the brain are arranged in a hierarchy

Sample illustration of hierarchical processing*

*Idea borrowed from Hugo Larochelle’s lecture slides

Layer 1: detect edges & corners

Layer 3: detect high level objects, faces, etc.

Layer 2: form feature groups

Disclaimer

I understand very little about how the brain works!

What you saw so far is an overly simplified explanation of how the brain works!

But this explanation suffices for the purpose of this course!

Module 2.2: McCulloch Pitts Neuron

McCulloch (neuroscientist) and Pitts (logician) proposed a highly simplified computational model of the neuron (1943)

\(y = 0\) if any \(x_i\) is inhibitory, else

\(\theta\) is called the thresholding parameter

This is the thresholding logic

\(f\)

\(g\)

\(x_1\)

\(x_2\)

\(x_n\)

..

..

\(y\in \lbrace0,1\rbrace\)

\(g\) aggregates the inputs

The inputs can be excitatory or inhibitory

\(\in \lbrace0,1\rbrace\)

and the function \(f\) takes a decision based on this aggregation

Let us implement some boolean functions using this McCulloch Pitts (MP) neuron ...

\(x_1\)

\(\theta\)

\(x_2\)

\(y\in \lbrace0,1\rbrace\)

\(x_3\)

* circle at the end indicates inhibitory input: if any inhibitory input is 1 the output will be 0

\(y\in \lbrace0,1\rbrace\)

\(x_1\)

\(x_2\)

\(x_3\)

\(x_1\)

\(x_2\)

\(y\in \lbrace0,1\rbrace\)

\(x_3\)

\(x_1\)

\(x_2\)