Variational Quantum Linear Solver for Multiphysics Problems (Final)
Mostafa Atallah
Cairo University
\frac{\partial^2 T}{\partial x^2} = 0
The Laplace Equation
T_{i+1} - 2T_{i}+ T_{i-1} = 0
apply FDM
\begin{pmatrix}
-2 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\
0 & -2 & 0 & 1 & 0 & 0 & 0 & 0\\
1 & 0 & -2 & 0 & 1 & 0 & 0 & 0\\
0 & 1 & 0 & -2 & 1 & 1 & 0 & 0\\
0 & 0 & 1 & 1 & -2 & 0 & 1 & 0\\
0 & 0 & 0 & 1 & 0 & -2 & 0 & 1\\
0 & 0 & 0 & 0 & 1 & 0 & -2 & 0\\
0 & 0 & 0 & 0 & 0 & 1 & 0 & -2
\end{pmatrix}
\begin{pmatrix}
T_{0} \\
T_{1} \\
T_{2} \\
T_{3} \\
T_{4} \\
T_{5} \\
T_{6} \\
T_{7}
\end{pmatrix}
=\begin{pmatrix}
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
0 \\
0
\end{pmatrix}
A x = b
A = 2 \left( I -0.125\; X_0 X_1 X_2 + 0.125 \; X_0 Y_1 Y_2 + 0.125 \; Y_0 X_1 Y_2 - 0.125 \; Y_0 Y_1 X_2 - 0.25 \; X_1 X_2 - 0.25 \; Y_1 Y_2 - 0.5 \; X_2 \right)
VQLS
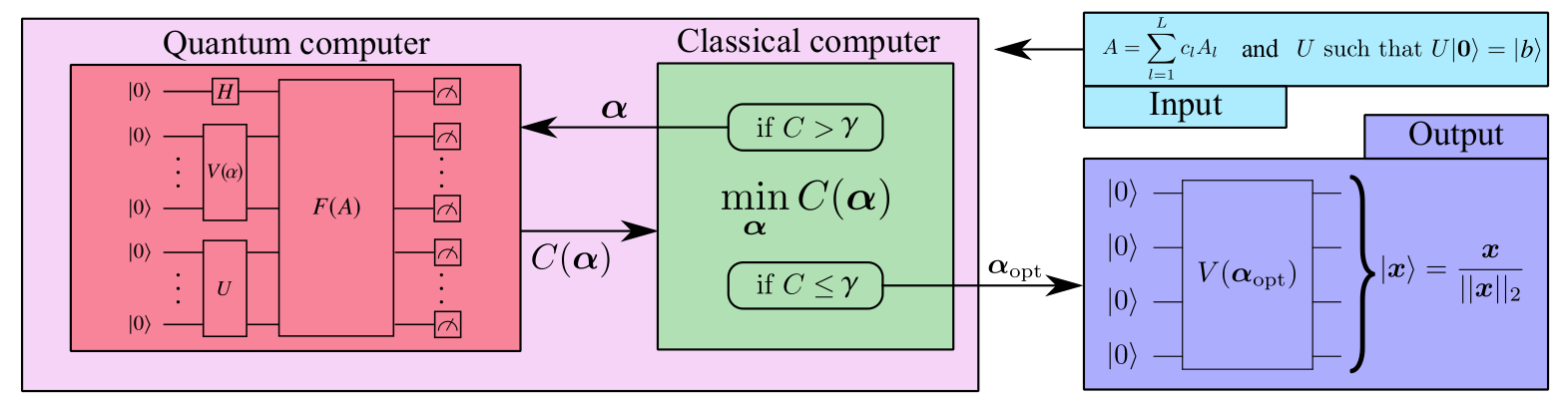
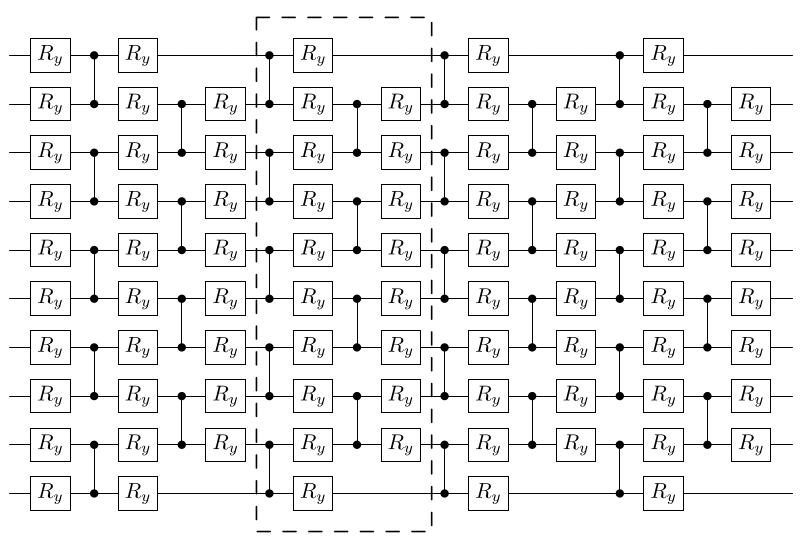
R_y(\alpha_i) = \mathbf{e}^{-\imath \; \alpha_i Y / 2}
V(\alpha)
\[ H = A^\dagger (\mathbb{I} - |b> <b|) A \]
\[ C = <x|H|x>\]
Cost Convergence
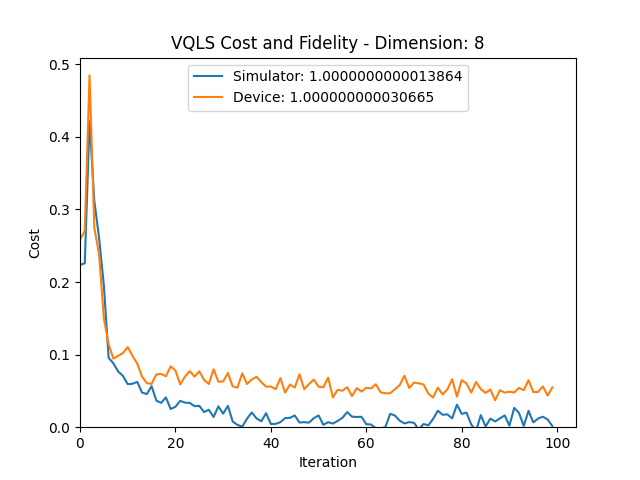
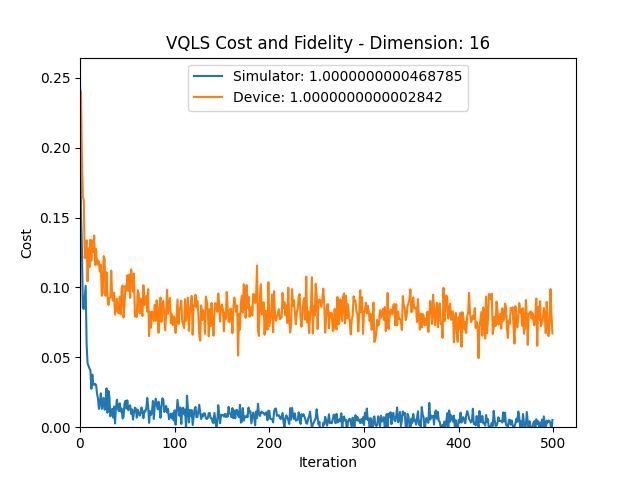
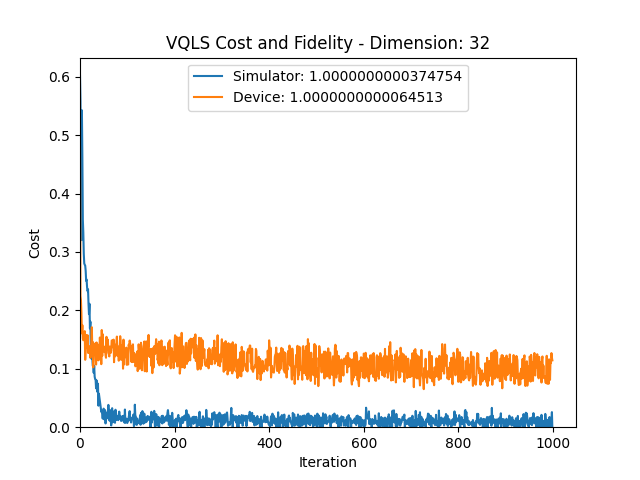
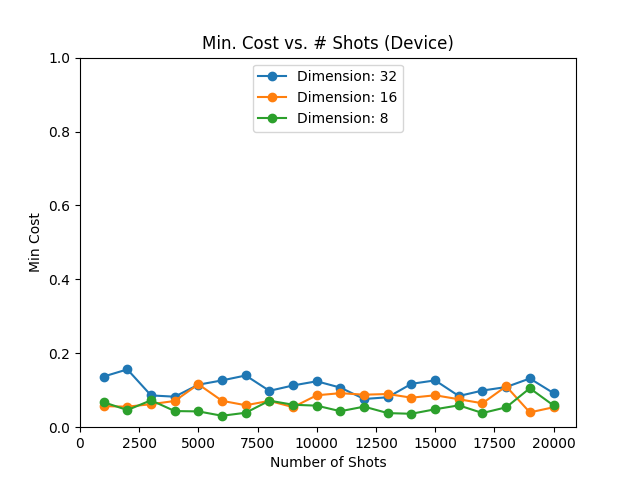
Cost vs. Shots
Goals Checklist
- Study and analyze the performance of the Variational Quantum Linear Solver (VQLS) in general.
- Solve some Multiphysics problems such as the Heat equation, etc. using VQLS.
- Execute the results using Qiskit on both a simulator and a device.
- Work with higher dimensions and employ Qiskit runtime and the local cost approach.
- Study quantum chip qubits connectivity and use the error mitigation techniques which can significantly improve expectation values and therefore the final fidelity.