Functional Programming
By
m.recachinas (at) gmail (dot) com
plan of attack
- Brief History
- Functional Concepts
- Demo
- ...
- Profit!

Brief history

Timeline
1930s – Alonzo Church & λ-calculus
1958 – John McCarthy & Lisp
1972 – Dennis Ritchie & C
(for perspective)
1973 – Robin Milner & ML
1977 – John Backus & Functional Programming
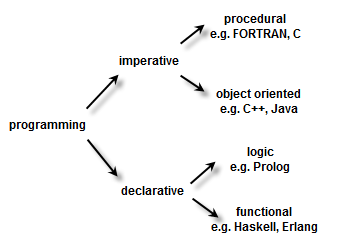
Programming language paradigms
DECLARATIVE:
Focus on the high-level "
what
"
FUNCTIONAL:
"subset" of Declarative*
Concepts

no side-effects
OCaml/Haskell
count :: List -> Int
When this function count runs on a List, we get back an Int. No more, no less.
C
int count(List l) { ... }
C++ however doesn't promise integrity. Maybe it's doing file IO or updating a global variable. You can't trust the code won't burn down your house.
Immutability
Given that FP seeks to eschew side effects, reassignment is usually not valid.
let x = 3;;
x = 4;; (* => bool = false, '=' here is actually testing equality *)
x := 4;;(* => Error: This expression has type int but an expression was
expected of type 'a ref *)
Also, as previously mentioned, functions do not mutate state, they only return new values.
let arr = [1; 2; 3] (* declare a list *)
double arr (* => [2; 4; 6], arr has not changed *)Lambda calculus
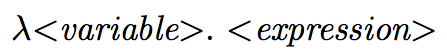
e.g.
λx. x == function(x) { return x; }
λx. y == function(x) { return y; }
λx. x UNICORN == function(x) { return x; }(UNICORN) // => UNICORN
λs. (s s) == function(f) { return f(f); }
λs. (s s) λs. (s s) == function(f) { return f(f); }(function(f) { return f(f); })=> λs. (s s) λs. (s s) => λs. (s s) λs. (s s) => ...
some formalisms
f :: A → B
f is a function mapping a set A to a set B
e.g.
add1 :: integer → integer
add1 takes in an integer and returns an integer
functions
Higher-order Functions
functions that work on other functions; they take one or more functions as an argument and can also return a function.
map(function, array) # => new arrayFirst-class Functions
the language treats functions as values – you can assign a function to a variable, pass it around, return it, etc.
var f = function(x) { return 2 * x; };
var double = { name: 'double' };
double.fn = f;
double.fn(3) // => 6Quick Summary
Functional Programming...
Does not cause side effects
Functional Python

Map
map(function, iterable, ...)
What's its type?
map :: (a → b) → [a] → [b]
Example
def square(x): return x ** 2
map(square, [1, 2, 3, 4, 5]) # => [1, 4, 9, 16, 25]Reduce
reduce(function, iterable, initializer=None) What's its type?
reduce (aka fold) :: (a → b → b) → b → [a] → b def mult(x,y): return x * y
reduce(mult, [1, 2, 3, 4, 5], 1) # => 120Filter
filter(function, iterable)
What's its type?
filter : (a → boolean) → [a] → [a] def is_even(x): return x % 2 == 0
filter(is_even, [1, 2, 3, 4, 5]) # => [2, 4]Lambda Expressions

lambdas in Python are anonymous functions of the form
lambda arguments: expression def f(x): return x ** 2 # regular function
g = lambda x: x ** 2 # lambda, or anonymous function
f(8) # => 64
g(8) # => 64Lambdas cont'd
We can easily convert our previous examples to lambdas
map(lambda x: x ** 2, [1, 2, 3, 4, 5] # => [1, 4, 9, 16, 25]
reduce(lambda x,y: x * y, [1, 2, 3, 4, 5], 1) # => 120
filter(lambda x: x % 2 == 0, [1, 2, 3, 4, 5]) # => [2, 4]
You can also nest, or curry, them!
nest = lambda x: lambda y: lambda z: x + y + z
nest(1)(2)(3) # => 6list comprehensions
Follow mathematical set builder notation
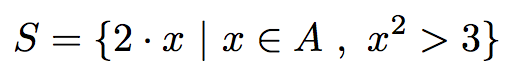
where A is some set
map() and filter() all in one!
a_list = [1, 2, 3, 4, 5]
S = [ 2 * x for x in a_list if x ** 2 > 3 ] # => [4, 6, 8, 10]def qsort(L):
if len(L) <= 1: return L
return qsort( [ lt for lt in L[1:] if lt < L[0] ] ) + \
[ L[0] ] + qsort( [ ge for ge in L[1:] if ge >= L[0] ] )
Generator expressions
Similar to list comprehensions, except using iterators
a_list = [1, 2, 3, 4, 5, 6]
S = ( 2 * x for x in a_list if x ** 2 > 3 ) # => <generator object
<genexpr> at 0x221164>
S.next() # => 4
S.next() # => 6
S.next() # => 8
S.next() # => 10
S.next() # => 12currying
Given a function f of type f : (X → Y) → Z, currying makes it into curry(f) : X → (Y → Z)
def make_incrementor(n): return lambda x: x + n
f = make_incrementor(1) # => (lambda x: x + 1)
g = make_incrementor(10)# => (lambda x: x + 10)
f(5) # => 6
g(5) # => 15
Decorators
def logger(func):
def inner(*args, **kwargs):
print "Arguments were: %s, %s" % (args, kwargs)
return func(*args, **kwargs)
return inner
@logger
def foo(x, y): return x * y
foo(5, 4) # => 20, output=Arguments were: (5, 4), {} @total_ordering # this is a decorator, you supply __eq__ and such
class Student:
def __eq__(self, other):
return ((self.lastname.lower(), self.firstname.lower()) ==
(other.lastname.lower(), other.firstname.lower()))
def __lt__(self, other):
return ((self.lastname.lower(), self.firstname.lower()) <
(other.lastname.lower(), other.firstname.lower()))functools
from functools import partialbasetwo = partial(int, base=2) # int takes in int(x, base=10) basetwo('10010') # => 18 Partial function application!
(Note: this is slightly different than currying*)
What's the type?
(((a → b) → c) → a) → (b → c) = λ(f, x). λy. f (x, y) // watimport itertools chain('ABC', 'DEF') # => A B C D E F
compress('ABCDEF', [1,0,1,0,1,1]) # => A C E F
dropwhile(lambda x: x<5, [1,4,6,4,1]) # => 6 4 1
ifilter(lambda x: x%2, range(10)) # => 1 3 5 7 9
ifilterfalse(lambda x: x%2, range(10)) # => 0 2 4 6 8
imap(pow, (2,3,10), (5,2,3)) # => 32 9 1000
starmap(pow, [(2,5), (3,2), (10,3)]) # => 32 9 1000
takewhile(lambda x: x<5, [1,4,6,4,1]) # => 1 4
izip('ABCD', 'xy') # => Ax By
izip_longest('ABCD', 'xy', fillvalue='-') # => Ax By C- D-
permutations('ABCD', 2) # => AB AC AD BA BC BD CA CB CD DA DB DC
combinations # => AB AC AD BC BD CD
combinations_with_replacement('ABCD', 2) # => AA AB AC AD BB BC BD CC CD DD
Functional JS

Similar to python
var arr = [1, 2, 3, 4, 5]
arr.map(function(element) { return Math.pow(element, 2); });
// => [1, 4, 9, 16, 25]; arr is still [1, 2, 3, 4, 5]
arr.filter(function(element) { return x % 2 === 0; });
// => [2, 4]; arr is still [1, 2, 3, 4, 5]
arr.reduce(function(prev, current, index, array) {
return prev * current;
});
// => 120; arr is still [1, 2, 3, 4, 5]Notice the anonymous functions?
$('#yolo').click( function() { // Even in jQuery too!
alert("swag!")
});
closures
Whenever you see the function keyword within another function, the inner function has access to variables in the outer function.
This creates a closure. You can use this to curry.
var add = function(x) {
return function(y) {
return x + y;
}
};
var incrementor = add(1);
incrementor(5) // => 6compose
a() b() c()
↓
Composition
↓
a(b(c(x))) == compose(a, b, c)(x)
var add1 = function add1(x) { return x + 1; };
var add3 = compose(add1, add1, add1);
add3(0) // => 3 var addSalutation = function(x) { return 'G`day, ' + x; };
var addTitle = function(x) { return 'Mr. ' + x; };
var meetAndGreet = compose(addSalutation, addTitle);
addSalutation(addTitle('Baggins')); // => G`day, Mr. Baggins
meetAndGreet('Baggins'); // => G`day, Mr. Bagginsabc's
var friendlyGreet = function(somebody) {
alert("Hi, " + somebody.name + ", I'm " + this.name);
};
Apply - calls the same function with the params (this, [args specified in an array])
friendlyGreet.apply(Bob, [Alice]); // => "Hi, Alice, I'm Bob" Bind - returns a function that will act like the original function but with this predefined
friendlyGreet.bind(Bob)(Alice); // => "Hi, Alice, I'm Bob"
Call - calls the same function with the specified arguments, beginning with this.
friendlyGreet.call(Bob, Alice); // => "Hi, Alice, I'm Bob"
friendlyGreet.bind(Bob).call(Alice, Bob); // => "Hi, Bob, I'm Bob"
external libraries
Tons of very good libraries
A bit of Ocaml
(with just a smidge of Haskell)

OCaml in a nutshell
- OCaml is a statically typed, interpreted and compiled language
-
Integers are 31-bits and 63-bits (Why?!)
- OCaml is slower than C, but faster than C++ (Whaa??!)
(* Comments can (* be (* nested *) *) *)
let x = ... (* This is how you define an immutable variable *)
(* The compiler infers type, so you don't need annotations! *)
let x = ref ... (* This is a reference, similar to pointers in C/C++ *)
let y = !x (* This is how you access a referenced value *)
x := !x + 1 (* This will change the contents of x to (x+1) *)
let double x = 2 * x (* == int double(x){ return 2*x; } *)
let rec fact x = function (* You have to denote recursive functions *)
| 0 -> 1 (* Pattern matching!! *)
| n -> n * fact (n-1)
examples
Pattern Matching
let rec last = function
| [ ] -> None
| [a] -> Some(a)
| _ :: tl -> last tlFold - the most powerful function ever
let sum = List.fold_left (fun a x -> x + a) 0
let map f l = List.fold_right (fun x a -> (f x) :: a) l []
let rev l = List.fold_left (fun a x -> x :: a) [] l
let filter f l =
List.fold_right (fun x a -> if f x then x :: a else a) l []
Note: each of the above uses currying
Simple Binary Tree & height() in OCaml
type binarytree =
| Node of binarytree * int * Node of binarytree
| Leaf of int
let rec height tree = match tree with
| Leaf _ -> 1
| Node(x,_,y) -> 1 + max (height x) (height y)*Bonus* Quick Sort in Haskell
qsort [] = []
qsort (p:xs) = (qsort lesser) ++ [p] ++ (qsort greater)
where
lesser = filter (< p) xs
greater = filter (>= p) xsSo beautiful!
Advanced topics

typing
OCaml, like Haskell, has static typing alongside type inference - e.g. there is never confusion about types.
f x = 2 * x (* f :: Int → Int *)
In C, typing is static, but is weakly enforced.
printf("%d", 'c' + 5); // this shouldn't workPython & JS have dynamic typing (duck typing).
evaluation
strict
OCaml has strict evaluation.
lazy
Haskell has lazy evaluation.
Nothing is evaluated unless necessary, e.g.
head (sort lst) # will only be sorted enough to find the minimum [1..] # infinite data structure print len([1 + 1, 2 * 2, 3 / 0, 4 - 1]) # => ZeroDivisionError: ...Referential Transparency
Replace each reference to a variable with its definition
let y = 55;;
let f x = x + y;;
f 3;; (* => 3 + y => 3 + 55 => 58 *)
Tail Recursion
A function call is said to be tail recursive if there is nothing to do after the function returns except return its value
# ----- Recursive, but not tail recursive -----
def fact(n):
if n == 0: return 1
return n * fact(n - 1)
# ----- Tail Recursive -----
def fact1(n, accumulator):
if n == 0: return accumulator
return fact1(n - 1, n * accumulator)
def fact(n):
return fact1(n, 1)
monads
Don't ask me what a monad is.

(or ask me after)
potential speedups?
Could we parallelize map, fold, filter, etc.?
Python, OCaml, Haskell have libraries that do this.
For map and filter, this absolutely lends itself to parallel processing. To a lesser extent, same with fold.
Why?
functional C++

Just kidding
although there are lambdas in C++11...
[] () -> int { return 1; };
or
[] () { return 1; }; // compiler knows this returns an integer...
recap

It's often much easier to understand a function in functional programming, because it only touches what you see and it's harder to have hidden bugs and bad program state.
Abstraction is important because humans suck, and functional programming makes certain abstraction easier.
Immutability
keep concurrency predictable
Type Inference
keep code clean
First class functions
keep things flexible
Pattern Matching
keep your needles out of haystacks
Only Price
Complexity

- AT&T - Haskell to automate form processing
- Amazon - Erlang to implement SimpleDB (database services for EC2)
-
Bank of America & Merril Lynch - Haskell for data transformation & loading
- BAE Systems - Haskell for almost everything in their SAFE project
- Bloomberg - OCaml for advanced financial derivatives risk management
- Citrix - OCaml for a world class server virtualization system
- Ericsson - Erlang for its support nodes, used in GPRS and 3G mobile networks
-
Facebook - Haskell/OCaml for manipulating PHP codebase; Erlang for chat service
-
Google - Haskell for internal IT structure; MapReduce
- Intel - Haskell for part of their research on multicore parallelism at scale
-
Jane Street - OCaml for everything (infrastructure, trading, ops, accounting systems)
-
MITRE - Haskell for cryptographic protocol analysis
- Motorola - Erlang for call processing products in the public-safety industry
- NRAO - Haskell for core science algorithms in telescope scheduling system
-
NVIDIA - Haskell for in-house tools
- NY Times - Haskell to process images from 2013 New York Fashion Week
-
Qualcomm, Inc. - generate Lua bindings
- T-Mobile - Erlang for SMS and authentication systems
- Twitter/Linkedin/Foursquare - Scala for a ton of stuff
- Yahoo! - Erlang for its social bookmarking service, Delicious
our goal
We want to write beautiful and powerful code.
Functional programming lends itself to it.
References
- http://wikipedia.org
- http://shuklan.com/haskell/
- http://ocaml.org
- http://www.haskell.org
- http://stackoverflow.com/questions/1636455/where-is-erlang-used-and-why
- http://www.secnetix.de/olli/Python/lambda_functions.hawk
- http://www.cs.virginia.edu/~weimer/2014-4610/lectures/weimer-pl-02.pdf
- http://www.inf.ed.ac.uk/teaching/courses/inf1/fp/lectures/2012/lect01.pdf
- http://www.slideshare.net/al3x/why-scala-for-web-20
- http://www.slideshare.net/kaw2/cv-js-26316409
- http://code.activestate.com/recipes/66473-just-for-fun-quicksort-in-3-lines/
- http://simeonfranklin.com/blog/2012/jul/1/python-decorators-in-12-steps/
-
http://ua.pycon.org/static/talks/kachayev/
