ALGORYTM BADAJĄCY PRZYNALEŻNOŚĆ PUNKTU DO ODCINKA

Algorytmy sprawdzające przynależność danego punktu do różnych obszarów może być przydatna. Dobrym przykładem są przypadki, kiedy chcemy sprawdzić, czy moduł GPS znalazł się poza wyznaczonym obszarem.

poniżej przykład takiego algorytmu

Mamy odcinek AB, określony przez punkty A(Xa;Ya) i B(Xb;Yb). Sprawdzamy, czy punkt C(Xc;Xb) należy do tego odcinka.

Krok 1: Sprawdzamy, czy współrzędne punktu C spełniają warunek:

 

XbY+XaYb+XYa-XaY-XbYa-XYb=0

KROK 2: Jeśli tak, to punkt C przynależy do prostej zawierającej odcinek AB, teraz sprawdzamy kolejne warunki ->

Xc ≥ min(Xa,Xb)

Xc ≤ max(Ax,Xb)

Yx ≥ min(Ya,Yb)

Yx ≤ max(Ya,Yb)

ALGORYTM BADAJĄCY POŁOŻENIE PUNKTU WZGLĘDEM PROSTEJ

Najprostsza możliwość jest taka, kiedy punkt ma współrzędne c,y, a prosta jest opisana wzorem x=c. Wtedy wszystkie punkty należą do tej prostej.

W innym przypadku możemy posłużyć się algorytmem.

poniżej przykład takiego algorytmu

Dana jest prosta  y=ax+b. a i b to liczby rzeczywiste.

 

Krok 1: Podstawiamy współrzędne punktu do równania i sprawdzamy, czy spełnia jego warunek.

Krok 2: Do zmiennej możemy podstawić wartość wyrażenia.

Krok 3: Jeśli Yp (współrzędna punktu) spełnia to wyrażenie, to punkt należy do prostej.

ALGORYTM OBLICZAJĄCE POLE OBSZARU OGRANICZONEGO

Zagadnienie polega na pokryciu obszaru, który chcemy obliczyć prostokątami i obliczenie ich pola powierzchni. Im więcej figur użyjemy, tym dokładniejszy będzie wynik.

poniżej przykład takiego algorytmu

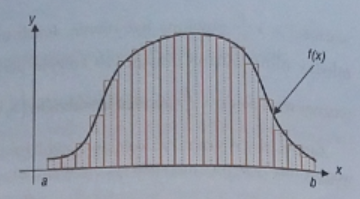
Dany jest obszar wydzielony osią X, wykresem funkcji i prostymi a i b.

Krok 1: Określamy szerokość pojedynczego prostokąta.

Krok 2: Wyznaczamy wysokość

prostokąta, która jest wartością

funkcji w danym punkcie.

Krok 3: Obliczamy sumę pól

powierzchni wszystkich

prostokątów.

w=(b-a)/n