Intro to Graphs
Muhammad Magdi
Agenda
- Motivation
- Graph Terminology
- Graph Classification
- Graph Representation
- Graph Traversal
- Common Problems
Hundreds of interesting computational problems are
couched in terms of graphs.--CLRS
Graphs have applications in a host of different domains,
including mapping, transportation, electrical engineering, and computer networks.--Data Structures and Algorithms in C++
Pairwise connections between items play a critical role in a vast array of computational applications.
--Algorithms Book
Motivation
Motivation

- What's the shortest route from Cairo to Alex?
- What's the fastest way to get from Cairo to Alex?
- What's the min cost to ship some orders from a group of warehouses to the customres?
- Is there a short-circuit in a given circuit?
- Can a given circuit be put onto a chip without crossing wires?
- How to match some people with their limited interest list?
- How to send this peace of info through internet with minimum latency?
- How can a compiler build a modular system?
- How to suggest friends in a social network?
- and more...
Graph Terminology
Nodes/Vertices (n)
Usually used to represent object in a given problem
Edges/Arcs (m)
Usually used to represent relationships between those objects (nodes)
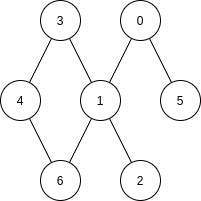
Graph
A way of representing relationships between pairs of objects. Visualized as circles connected by lines representing nodes and edges respectively

Nodes a, b are called adjacents (Neighbors), iff there's a direct edge between them.

Adjacency Relation
A sequence of nodes connected by edges.
Path
A Path whose first and last nodes are the same.
Cycle
A graph having multiple edges between the same pair of nodes.
Multigraph
An edge connecting a node to itself.
Self-loop
A graph that's neither multigraph nor having self-loops.
Simple Graph
Graph Classification
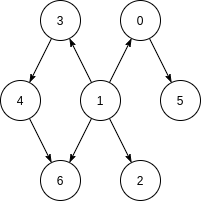
Directed
A graph whose all edges are having directions.
Undirected
A graph whose all edges are NOT having directions.

Graph Classification
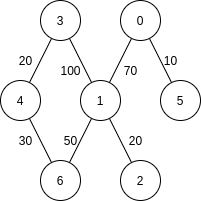
Weighted
A graph having a weight (number) associated with each edge.
Unweighted
A graph whose all edges are considered equivalent in length (weight).


Graph Classification
Connected
A graph in which there's a path between every pair of nodes.
Disconnected
A graph consisted of a set of connected components (subgraphs).

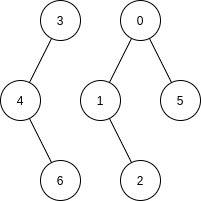
Graph Classification
Cyclic
Acyclic
A graph with no cycles.


A graph that is/contains a cycle.
Graph Classification
Dense
A graph having a relatively few of the possible edges missing
Sparse
A graph having a relatively few of the possible edges present

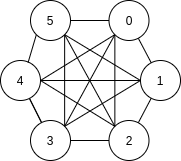
Graph Classification
Explicit
Implicit
A graph whose nodes or edges are not explicitly represented as objects in computer memory, but are determined algorithmically in runtime from some input.
--Wikipedia

Graph Classification
Special Types of Graphs
A graph in which each pair of nodes is directly connected by an edge
Complete Graph

Special Types of Graphs
The most dense graph

A graph that can be divided into 2 sets such that there's no edge between nodes within the same set.
Bipartite Graph
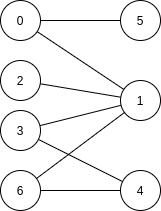
Special Types of Graphs
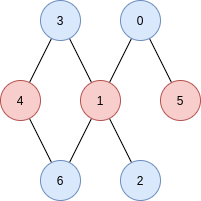
- Connected Acyclic Graph
- Undirected Graph in which there's exactly one unique path between each pair of nodes
that means:
1. One Connected Component
2. Edges = nodes - 1
3. Acyclic
Tree Graph
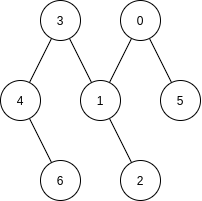
Special Types of Graphs
Directed Acyclic Graph
DAG
Special Types of Graphs
