Dataset Sensitive Autotuning of Multi-Versioned Code based on Monotonic Properties

Autotuning in Futhark

Art by Robert Schenck

Philip Munksgaard, Svend Lund Breddam, Troels Henriksen, Fabian Cristian Gieseke & Cosmin Oancea

A general method for finding the near-optimal* tuning parameters for multi-versioned code

* Subject to some assumptions

A general method for finding the near-optimal* tuning parameters for multi-versioned code

  • A way of choosing at run-time between multiple semantically identical but differently optimized versions of code
  • Generalizes to all programs that are structured in a similar way
  • Is implemented as part of the Futhark project
  • Functional languages are ideal for experimenting with generating different code versions

This talk

  • Motivation and running example
  • Autotuning
  • Results
  • Related work
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

Two levels of parallelism

  • Outer parallelism
    • Degree m
  • Inner parallelism
    • Degree n
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

  • There could be any number of levels of parallelism in the code
  • Hardware has limited number of levels of parallelism
  • How do we map code to hardware?
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

Ways to parallelize

  • Parallelize outer, sequentialize inner
  • Parallelize inner, sequentialize outer
  • There are more ways
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

Tall matrix?

mm threads, sequential inner code

n=5n = 5
n = 5
m=100m = 100
m = 100
let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

nn threads,

sequential outer code

n=100n = 100
n = 100
m=5m = 5
m = 5

Wide matrix?

let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

So which version to use?

 

Inner or outer?

let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

We don't know at compile-time!

let mapscan [m][n] (xss: [m][n]i32) : [m][n]i32 =
    map2 (\(row: [n]i32) (i: i32) ->
            loop (row: [n]i32) for _ in 0..<64 do
              let row' = map (+ i) row
              in scan (+) 0 row'
         )
         xss (0..<m)

An example

Instead, let's generate multiple versions, and choose at compile-time

Henriksen, Troels, et al. "Incremental flattening for nested data parallelism." Proceedings of the 24th Symposium on Principles and Practice of Parallel Programming. 2019.

Incremental flattening!

m≥tm \geq t
m \geq t

Parallelize outer

Parallelize inner

true

false

An example

Incremental flattening!

m≥tm \geq t
m \geq t

Parallelize outer

Parallelize inner

true

false

An example

Incremental flattening!

  • Generate multiple different versions of code
  • Right-leaning tree
  • pp was degree of parallelism of left child, but can be any scalar known at run-time
  • tt is "user-defined" threshold
p1≥t1p_1 \geq t_1
p_1 \geq t_1

true

false

p2≥t2p_2 \geq t_2
p_2 \geq t_2

Version 2

true

false

Version 3

Version 1

An example

p1≥t1p_1 \geq t_1
p_1 \geq t_1

true

false

p2≥t2p_2 \geq t_2
p_2 \geq t_2

Version 2

true

false

Version 3

Version 1

But how do we determine set of tt that gives us best performance, for all datasets?

  • Really an optimization problem
  • Minimize number of test-runs

Autotuning

Assumptions

  • Right-leaning tree, but generalizes to forests
  • A single unknown per threshold/branch
  • Monotonicity requirement
  • Compiler instrumentation
  • Representative datasets
p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Size-invariance

  • Size-invariant: During the execution of a certain dataset, pip_i is constant

 

p1p_1 can be size-variant and p2p_2 can be size-invariant on a certain dataset

 

Analysis is done per-threshold

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Size-invariance

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
n=100n = 100
n = 100
m=5m = 5
m = 5

Input:

p1p_1 is height of matrix (mm)

So the size is invariant

55
5
p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Size-invariance

What if there's a loop?

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

What if there's a loop?

loop:
n=100n = 100
n = 100
m=5m = 5
m = 5

Input:

n=100n = 100
n = 100
m=5m = 5
m = 5
n=100n = 100
n = 100
m=5m = 5
m = 5
n=100n = 100
n = 100
m=5m = 5
m = 5
{5,5,5,5}\{5, 5, 5, 5\}
\{5, 5, 5, 5\}

Still invariant

Size-invariance

Size-invariant tuning

For each dataset, a single code version is best

Therefore, to tune a program on a single dataset, run each code version once and pick thresholds such that the fastest version is executed

To tune a program on multiple datasets, tune individually and combine thresholds, somehow

Autotuning a single dataset

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

How do we make sure each version is run exactly once?

Program and dataset is given as is, we only control thresholds

Bottom-up traversal of the tuning tree

Autotuning a single dataset

Setting all thresholds to ∞\infty forces the bottom-most version to run

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
t1t_1
t_1
t2t_2
t_2

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Setting all thresholds to ∞\infty forces the bottom-most version to run

∞\infty
\infty
∞\infty
\infty

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Setting all thresholds to ∞\infty forces the bottom-most version to run

∞\infty
\infty
∞\infty
\infty

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Setting all thresholds to ∞\infty forces the bottom-most version to run

∞\infty
\infty
∞\infty
\infty

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Setting all thresholds to ∞\infty forces the bottom-most version to run

∞\infty
\infty
∞\infty
\infty

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Setting all thresholds to ∞\infty forces the bottom-most version to run

∞\infty
\infty
∞\infty
\infty

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Setting all thresholds to ∞\infty forces the bottom-most version to run

∞\infty
\infty
∞\infty
\infty

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Setting all thresholds to ∞\infty forces the bottom-most version to run

∞\infty
\infty
∞\infty
\infty

This allows us to record the run-time of v3v_3

With a bit of compiler instrumentation, we can also get information about what p1p_1 and p2p_2 was when they were compared against the thresholds

This allows us to pick v2v_2 next

p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Setting t2=100t_2 = 100 (or any value below that) will force execution of v2v_2

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Setting t2=100t_2 = 100 (or any value below that) will force execution of v2v_2

100100
100

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Setting t2=100t_2 = 100 (or any value below that) will force execution of v2v_2

100100
100

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Setting t2=100t_2 = 100 (or any value below that) will force execution of v2v_2

100100
100

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Setting t2=100t_2 = 100 (or any value below that) will force execution of v2v_2

100100
100

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Setting t2=100t_2 = 100 (or any value below that) will force execution of v2v_2

100100
100

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100

Setting t2=100t_2 = 100 (or any value below that) will force execution of v2v_2

100100
100

Now, we can set the threshold t2t_2 optimally for the bottom-most branch

Any value for t2t_2 larger than 100 will select v3v_3. Any value lower than 100 will select v2v_2

Thus, the optimal choice is a range:

If v2v_2 is preferable, 0≤t2≤1000 \leq t_2 \leq 100

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
p2≥p_2 \geq
p_2 \geq
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10
p2=100p_2 = 100
p_2 = 100
100100
100

To continue tuning, collapse bottom nodes into one and repeat

Autotuning a single dataset

p1≥p_1 \geq
p_1 \geq
v1v_1
v_1
∞\infty
\infty
p1=10p_1 = 10
p_1 = 10

To continue tuning, collapse bottom nodes into one and repeat

v2′v_2'
v_2'

We already know the best run-time for v2′v_2', so we can jump straight to running v1v_1

Autotuning multiple datasets

For each dataset, we have found an optimal range for each threshold

We need to combine the tuning results from each dataset

Example:

Dataset 1: 0≤t2≤1000 \leq t_2 \leq 100 is optimal

Dataset 2 : 50<t2≤∞50 < t_2 \leq \infty is optimal

Intersecting those ranges, 50<t2≤10050 < t_2 \leq 100 is optimal for both datasets!

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Autotuning multiple datasets

But is there always a valid intersection?

Example:

Dataset 1: 0≤t2≤1000 \leq t_2 \leq 100

Dataset 2: 500<t2≤∞500 < t_2 \leq \infty

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Monotonicity assumption

p1≥t1p_1 \geq t_1
p_1 \geq t_1
v1v_1
v_1
v2v_2
v_2

p1p_1 represents parallelism of v1v_1

If v1v_1 is faster than v2v_2 for a given value of p1p_1, it should also be faster for larger values

p1p_1 could represent something else, but we assume that the same property holds

Monotonicity assumption

Besides, if no range intersection exists, no choice of t2t_2 will choose the best code version for all datasets

p1≥t1p_1 \geq t_1
p_1 \geq t_1
v1v_1
v_1
v2v_2
v_2

Size-invariant tuning

This method allows us to optimally tune size-invariant programs using exactly n×dn \times d runs

nn: number of code versions

dd: number of datasets

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
loop:

But the size can change

Size-variance

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
loop:

But the size can change

n=100n = 100
n = 100
m=5m = 5
m = 5

Input:

n=5n = 5
n = 5
m=100m = 100
m = 100
n=50n = 50
n = 50
m=50m = 50
m = 50
{5,50,100}\{5, 50, 100\}
\{5, 50, 100\}

This program is size-variant!

Size-variance

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
loop:
{5,5,5,5}\{5, 5, 5, 5\}
\{5, 5, 5, 5\}

Size-variance

When the program is size-invariant, there is always a single best version of the code for each dataset

Always prefer v1v_1 for this dataset

p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3
loop:
{5,50,100}\{5, 50, 100\}
\{5, 50, 100\}

Size-variance

When the program is size-variant, there is not always a single best version of the code for each dataset

When p1p_1 is 55 or 5050, prefer v1v_1 otherwise prefer v2v_2

Size-variant tuning

loop:
{5,50,100}\{5, 50, 100\}
\{5, 50, 100\}
p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

It's no longer enough to run each code version once for each dataset

Each dataset does not necessarily have a single best code version

n=100n = 100
n = 100
m=5m = 5
m = 5

Input:

n=5n = 5
n = 5
m=100m = 100
m = 100
n=50n = 50
n = 50
m=50m = 50
m = 50

Size-variant tuning

loop:
p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Each dataset does not necessarily have a single best code version

Best for p2=50,100p_2 = 50, 100

Best for p2=5p_2 = 5

Result is still a range, and combining results is still the same, but how do we efficiently find the best range for each dataset?

Size-variant tuning

loop:
p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Best for p2=50,100p_2 = 50, 100

Best for p2=5p_2 = 5

Only values in {0,5,50,100,∞}\{0, 5, 50, 100, \infty\} are relevant to test

There could be many values. A loop that iterates a million times?

Binary search!

Size-variant tuning

loop:
p1≥t1p_1 \geq t_1
p_1 \geq t_1
p2≥t2p_2 \geq t_2
p_2 \geq t_2
v1v_1
v_1
v2v_2
v_2
v3v_3
v_3

Best for p2=50,100p_2 = 50, 100

Best for p2=5p_2 = 5

Binary search!

0,5,50,100,∞0, 5, 50, 100, \infty
0, 5, 50, 100, \infty

Measure

Measure

Measure

Gradient

Assuming such a gradient exists!

Size-variant tuning

If a gradient exists, we find the optimal tuning range for a single dataset and threshold in O(log⁡p)O(\log p) runs

pp: number of distinct parameter values for the given threshold

Results

Compare to previous tuning tool, based on OpenTuner

  • Black box
  • No knowledge of program structure
  • Explores enormous search space
  • Optimized with memoization

Tuning-time Results

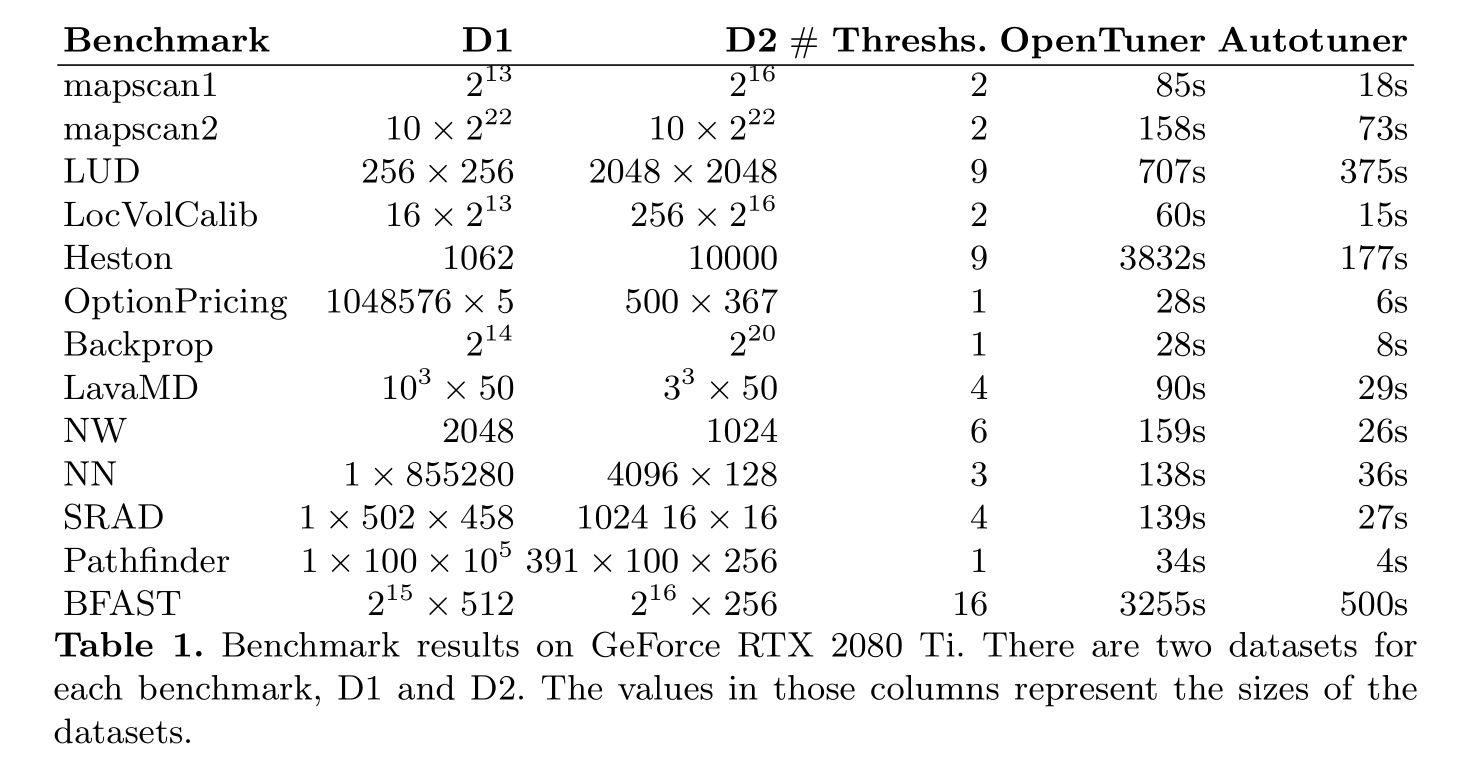
Performance of tuned program

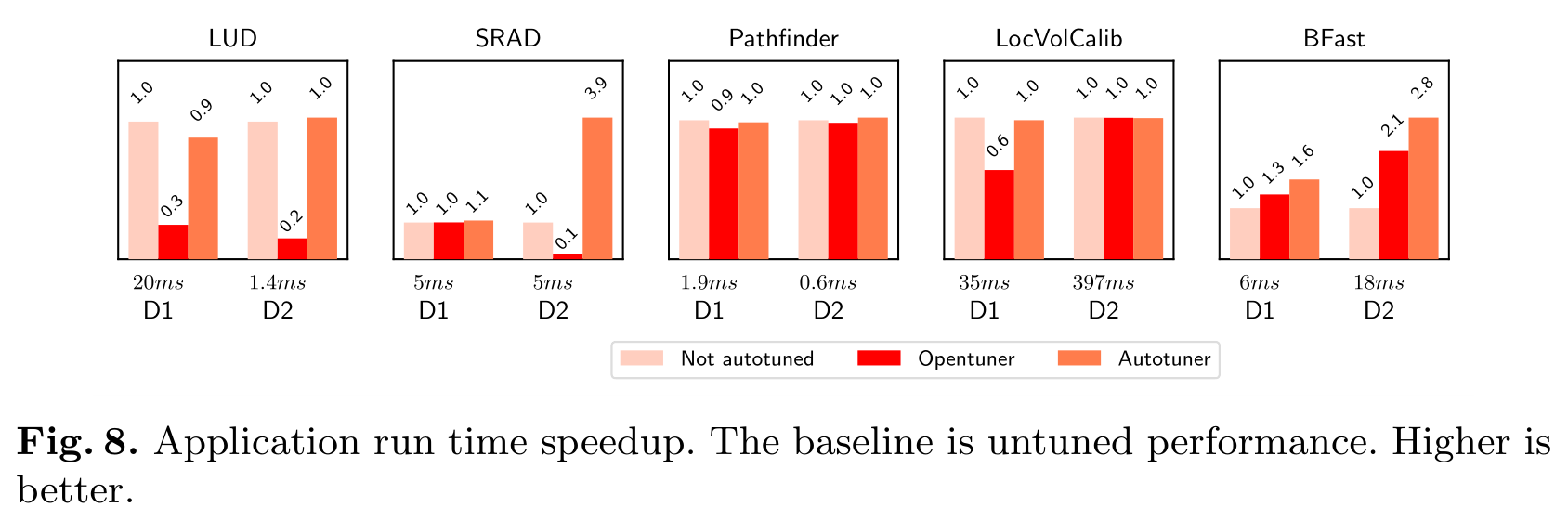
Only benchmarks which have different performance

Reliable even for programs with small number of thresholds

Other approaches

  1. Tune compiler flags for best average performance1^1
  2. Multi-versioned compilation, tune for a  single dataset on specific hardware
    • LIFT3,4^{3,4}, SPIRAL5^5
  3. General black-box tuning
    • OpenTuner6^6
  1. FURSIN, Grigori, et al. Milepost gcc: Machine learning enabled self-tuning compiler. International journal of parallel programming, 2011, 39.3: 296-327.
  2. STEUWER, Michel, et al. Generating performance portable code using rewrite rules: from high-level functional expressions to high-performance OpenCL code. ACM SIGPLAN Notices, 2015, 50.9: 205-217.
  3. HAGEDORN, Bastian, et al. High performance stencil code generation with Lift. In: Proceedings of the 2018 International Symposium on Code Generation and Optimization. 2018. p. 100-112.
  4. FRANCHETTI, Franz, et al. SPIRAL: Extreme performance portability. Proceedings of the IEEE, 2018, 106.11: 1935-1968.
  5. ANSEL, Jason, et al. Opentuner: An extensible framework for program autotuning. In: Proceedings of the 23rd international conference on Parallel architectures and compilation. 2014. p. 303-316.

Conclusion

Our technique combines multi-versioned compilation with a one-time autotuning process producing one executable that  selects the most efficient combination of code versions for any dataset.

  • Co-design between compiler and tuner
  • One variable per threshold
  • Maybe there is no intersection
  • But in practice it works

Thank you for listening

Made with Slides.com