fastTextに学ぶ高速化

自己紹介

中西克典(@n_kats_)
数学していました
たまにQiitaに書いています

fastTextとは

facebook製
自然言語処理
単語のベクトル化ができる
文章の分類ができる

単語のベクトル化

単語に意味が現れそうなベクトルを対応させる
word2vecが有名
製作者のトマス・ミコロフ氏はfastTextにも
CBOW
skip-gram

fastTextを試す

ソースがgithubにある
facebookresearch/fastText
詳細はREADMEに
〇〇.shを動かす
とても大きなデータをDLすることになるので注意
学習済みデータも数Gするので注意

fastTextの特徴

速い
CPUで高性能を挙げる
C++11(標準ライブラリのみ)
大量のクラスへの分類の技術とも見れる
（大量にある単語のどれが来るかの推測など）

モデル（言語部分）

CBOW
skip-gram
文章の分類

いずれのモデルも、単語などの配列を入力にして、単語やラベルを予想する

CBOW
周りの単語から中心に来る単語を推測する
skip-gram
中心の単語から周りの単語を推測する

文章の分類

学習データには教師データが必要
（その文章がどのクラスになるかの情報が必要）
__label__1のような単語を追加したデータを使う
入力は、文章を単語の配列だと思って扱う
ラベルは一つの文章に複数あってもOK

モデル（学習）

softmax regression（速くない）
negative sampling
階層的softmax

メインは階層的softmax。

いずれのモデルも

入力（単語の列）

→　各単語をベクトル化

→　平均を取る

→　線形な処理

→　非線形な処理で確率に

数学的に整理し直すと

入力（単語などの列）

→　単語などに対応するone-hotベクトルの
　　平均をとる

→　行列をかける

→　softmaxやsigmoidを適用する

（→　目的の確率の形に直す）

\frac{1}{N}(\cdots 1\ 0\ 1\cdots) \begin{pmatrix} & & \\ & & \\ & & \\ & & \\ \end{pmatrix} \begin{pmatrix} & & & & & \\ & & & & & \end{pmatrix}

\frac{1}{N}(\cdots 1\ 0\ 1\cdots) \begin{pmatrix} & & \\ & & \\ & & \\ & & \\ \end{pmatrix} \begin{pmatrix} & & & & & \\ & & & & & \end{pmatrix}

行列をかけている部分の模式図

（入力）m次元

m×h行列

ｈ×n行列

行列を二回かける意味は、

中間の次元を小さくすることで

パラメータの数を減らすことができる

m, h, nを入力・中間・出力の次元とすると

中間がないとm×n

中間があると(m+n)×h

階層的softmax

二分木を使って各クラスになる確率を決定する

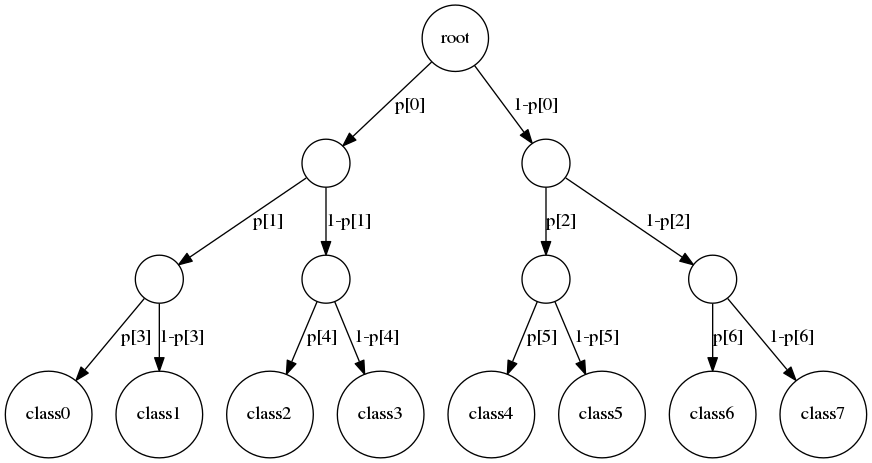
階層的softmaxでは、

いきなり、目的の確率を計算するのではなく、

左右どちらを選ぶかの確率を一度計算する。

（行列をかけた後、sigmoid関数を使う）

学習も目的のクラスにたどり着く経路にある分岐だけを学習すれば良い。

分岐の数をnとすると、

学習すべき分岐の数はlog nのオーダー。

fastTextの場合では

x: 入力(one-hotベクトルの平均)

A: 一つ目の行列

B: 二つ目の行列

p: 分岐で左を選ぶ確率

p = \mathrm{sigmoid}(x A B)

p = \mathrm{sigmoid}(x A B)

\frac{1}{N}(\cdots1\ 0\ 1\ \cdots) \begin{pmatrix} & & \\ & & \\ & & \\ & & \\ \end{pmatrix} \begin{pmatrix} & & & & & \\ & & & & & \end{pmatrix}

\frac{1}{N}(\cdots1\ 0\ 1\ \cdots) \begin{pmatrix} & & \\ & & \\ & & \\ & & \\ \end{pmatrix} \begin{pmatrix} & & & & & \\ & & & & & \end{pmatrix}

学習で更新する部分の模式図

他との比較

softmax
右の行列のすべての項目を更新する必要がある
negative sampling
二分木は使わないが、右の行列の更新が一部で済む

\mathrm{softmax}(x) = \left(\frac{e^{x_1}}{\sum_{k=1,\ldots,n}{e^{x_k}}}, \ldots, \frac{e^{x_n}}{\sum_{k=1,\ldots,n}{e^{x_k}}}\right)

\mathrm{softmax}(x) = \left(\frac{e^{x_1}}{\sum_{k=1,\ldots,n}{e^{x_k}}}, \ldots, \frac{e^{x_n}}{\sum_{k=1,\ldots,n}{e^{x_k}}}\right)

なぜ高速化が必要か

単純に単語だけでなく、単語の一部を取り出したsubwordを入力に使っている。(n-gram)

パターンが一気に増える。

本当は、単語とsubwordの列から推測を行う。

例(subword)

s,u,b,w,o,r,d,

su,ub,bw,wo,or,rd,

sub,ubw,bwo,wor,ord,

subw,ubwo,bwor,word,

subwo,ubwor,bword,

subwor, ubword

subword

実際は長さを制限する

ハッシュ化

単語やsubwordにIDを割り当てたい。

順番にIDを振ると探すのが大変。

文字列から計算で、IDを割り当てよう。

単語のIDが被るとまずいから、被ったらずらす。

subwordのハッシュは被っても気にしない。

ハッシュの値の許容範囲には制限をかける。

数百万まで許すと、学習データがでかくなる。

高速化に工夫が必要。

まとめ・感想

疎なものにすると高速化する
階層的softmaxでそれが実現される
機械学習はまだまだ進化しそう