On the Random

Subset Sum Problem

and Neural Networks

Emanuele Natale jointly with A. Da Cunha & L. Viennot

23 March 2023

Deep Learning on the Edge

Turing test (1950)

Today

1st AI winter (1974–1980)

2nd AI winter (1974–1980)

"A hand lifts a cup"

©️ Google's Imagen Video

Use of GPUs in AI (2011)

Today, most AI heavy lifting is done in the cloud due to the concentration of large data sets and dedicated compute, especially when it comes to the training of machine learning (ML) models. But when it comes to the application of those models in real-world inferencing near the point where a decision is needed, a cloud-centric AI model struggles. [...] When time is of the essence, it makes sense to distribute the intelligence from the cloud to the edge.

ARM Blueprint Blog

Roadmap

1. ANN pruning

2. The Strong Lottery Ticket Hypothesis

3. SLTH for CNNs

4. Neuromorphic hardware

Dense ANNs

Feed-forward homogeneous dense ANN \(f\):

Application of \(\ell\) layers \(N_i\) with

\(N_i(x) = \sigma(W_i x)\),

ReLu activation \(\sigma(x)=\max(0,x)\)

and weight matrices \(W_i\), so that

\[f(x)=\sigma(W_{\ell}(\sigma(W_{\ell-1}(...(x)))).\]

Compressing ANN

Matrix techniques

E.g. DLRT by Schotthöfer et al. Neurips 2022.

Quantization techniques

E.g. GPT3.int8() by Dettmers et al. Neurips 2022.

Pruning techniques

E.g. SPDY by Frantar et al. ICML 2022.

Neural Network Pruning

Blalock et al. (2020): iterative magnitude pruning still SOTA pruning technique.

train

prune

train

The Lottery Ticket Hypothesis

Frankle & Carbin (ICLR 2019):

Large random networks contains sub-networks that reach comparable accuracy when trained

train

sparse random network

sparse

bad network

..., train&prune

train&prune, ...,

large random network

sparse good network

train

sparse "ticket" network

sparse

good network

rewind

Roadmap

1. ANN pruning

2. The Strong Lottery Ticket Hypothesis

3. SLTH for CNNs

4. Neuromorphic hardware

The Strong LTH

Ramanujan et al. (CVPR 2020) find a good subnetwork without changing weights (train by pruning!)

A network with random weights contains sub-networks that can approximate any given sufficiently-smaller neural network (without training)

Formalizing the SLTH

Random network \(R_0\) with \(h\cdot d\) parameters

lottery ticket

\(N_{L}\subseteq N_0\)

Target network that solves task \(N_T\)

with \(d\) parameters

\approx

Proving the SLTH

Malach et al. (ICML 2020)

w_1

w_n

Find random weight

close to \(w\)

Idea: Find patterns in the random networks which are equivalent to sampling a weight until you are lucky.

Q: How many uniform\((-1,1)\) sample to approximate \(z\) up to \(\epsilon\)?

Malach et al.'s Idea

Suppose \(x\) and all \(w'_i\)s are positive, then

\[y=\sum_i w_i\sigma(w'_i x) = \sum_i w_i w'_i x \]

For general \(x\), use the ReLu trick \(x=\sigma(x)-\sigma(-x)\):

\[y= \sum_{i:w'_i\geq 0} w_i\sigma(w'_i x)+\sum_{i:w'_i<0} w_i\sigma(w'_i x) \]

\[= \sum_{i:w'_i\geq 0} w_i w'_i x {\mathbb 1}_{x\geq 0}+\sum_{i:w'_i<0} w_i w'_i x {\mathbb 1}_{x< 0}\]

w_1

w_n

w'_n

w'_1

Better Bound for SLTH

(assume \(x\) and \(w'_i\)s are positive)

\(y= \sum_{i} w_i w'_i x \)

Pensia et al. (NeurIPS 2020)

Find combination of random weights close to \(w\)

alternative in Orseau et al. (Neurips 2020)

w_1

w_n

w'_n

w'_1

RSSP. Given \(X_1,...,X_n\) i.i.d. random variables, with prob. \(1-\epsilon\) for each \(z\in [-1,1]\) find a subset \(S\subseteq\{1,...,n\}\) such that \(|z-\sum_{i\in S} X_i |\leq \epsilon.\)

Lueker '98. Solution exists with prob. \(1-\epsilon\) if \(n=O(\log \frac 1{\epsilon})\).

RSS - Proof Idea 1/2

If \(n=O(\log \frac 1{\epsilon})\), given \(X_1,...,X_n\) i.i.d. random variables, with prob. \(1-\epsilon\) for each \(z\in [-\frac 12, \frac 12]\) there is \(S\subseteq\{1,...,n\}\) such that \(|z-\sum_{i\in S} X_i |\leq \epsilon.\)

Let \(f_t(z)=\mathbf 1(z\in (-\frac 12, \frac 12),\exists S\subseteq\{1,...,t\}: |z-\sum_{i\in S} X_i |\leq \epsilon)\)

then \(f_t(z)=f_{t-1}(z)+(1-f_{t-1}(z))f_{t-1}(z-X_t)\).

Observation: If we can approximate any \(z\in (a,b)\) and we add \(X'\) to the sample, then we can approximate any

\(z\in (a,b) \cup (a+X',b+X')\).

RSS - Proof Idea 2/2

\(z\in(-\frac 12, \frac 12), f_t(z)=f_{t-1}(z)+(1-f_{t-1}(z))f_{t-1}(z-X_t)\).

\(\int_{-\frac 12}^{\frac 12}f_{t-1}(z)dz+\mathbb E[\int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))f_{t-1}(z-X_t)dz|\,X_{t-1},...,X_1]\)

\(=v_{t-1}+\frac 12 (1-v_{t-1})v_{t-1}.\)

\(=v_{t-1}+\frac 12 \int_{-1}^{1}[\int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))f_{t-1}(z-x)dz]dx\)

\(=v_{t-1}+\frac 12 \int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))[\int_{-1}^{1}f_{t-1}(z-x)dx]dz\)

\(=v_{t-1}+\frac 12 \int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))[\int_{z-1}^{z+1}f_{t-1}(s)ds]dz\)

\(=v_{t-1}+\frac 12 \int_{-\frac 12}^{\frac 12}(1-f_{t-1}(z))[\int_{-\frac 12}^{\frac 12}f_{t-1}(s)ds]dz\)

\(\mathbb E[v_t\,|\,X_{t-1},...,X_1]=\)

Let \(v_t=\int_{-\frac 12}^{\frac 12}f_t(z)dz\), then

"Revisiting the Random Subset Sum problem" https://hal.science/hal-03654720/

s = z-x

Roadmap

1. ANN pruning

2. The Strong Lottery Ticket Hypothesis

3. SLTH for CNNs

4. Neuromorphic hardware

Convolutional Neural Network

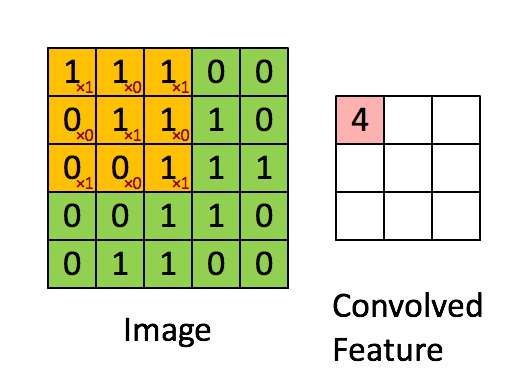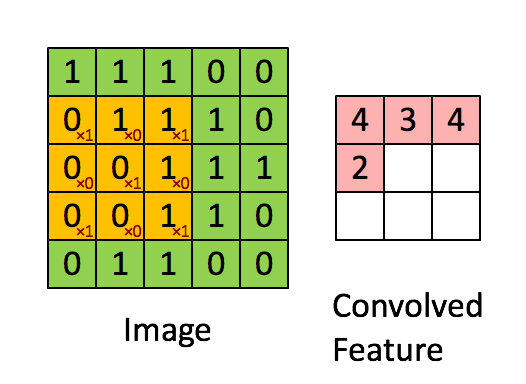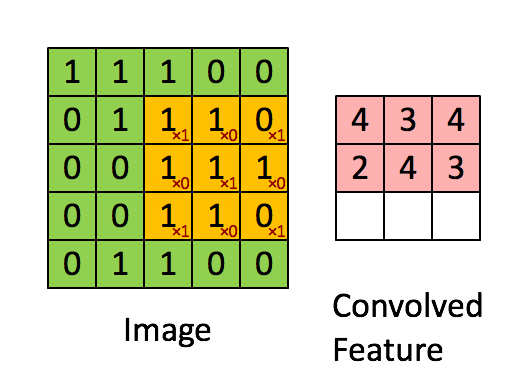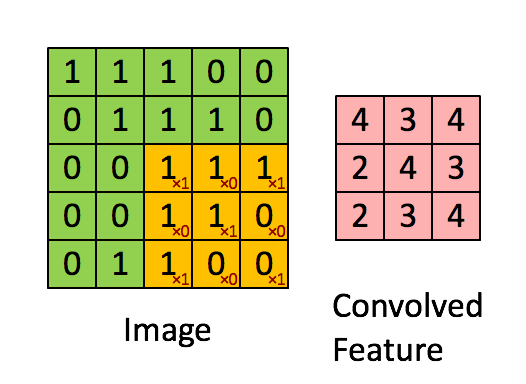
The convolution of \(K\in\reals^{d\times d\times c}\) and \(X\in\reals^{D\times D\times c}\) is \( \left(K * X\right)_{i,j\in\left[D\right]}=\)\[\sum_{i',j'\in\left[d\right],k\in\left[c\right]}K_{i',j',k}\cdot X_{i-i'+1,j-j'+1,k}, \]

where \(X\) is zero-padded.

A simple CNN \(N:\left[0,1\right]^{D\times D\times c_{0}}\rightarrow\mathbb{R}^{D\times D\times c_{\ell}}\) is defined as

\[ N\left(X\right)= \sigma\left( K^{(\ell)}*\sigma\left(K^{(\ell-1)}*\sigma\left(\cdots * \sigma\left(K^{(1)} * X\right)\right)\right)\right)\]

where \(K^{(i)} \in\mathbb R^{d_{i}\times d_{i}\times c_{i-1}\times c_{i}}\).

2D Discrete Convolution

If \(K\in\reals^{d\times d\times c_{0}\times c_{1}}\) and \(X\in\reals^{D\times D\times c_{0}}\)

\[ \left(K * X\right)_{i,j\in\left[D\right],\ell\in\left[c_{1}\right]}=\sum_{i',j'\in\left[d\right],k\in\left[c_{0}\right]}K_{i',j',k,\ell}\cdot X_{i-i'+1,j-j'+1,k}.\]

SLTH for Convolutional Neural Networks

Theorem (da Cunha et al., ICLR 2022).

Given \(\epsilon,\delta>0\), any CNN with \(k\) parameters and \(\ell\) layers, and kernels with \(\ell_1\) norm at most 1, can be approximated within error \(\epsilon\) by pruning a random CNN with \(O\bigl(k\log \frac{k\ell}{\min\{\epsilon,\delta\}}\bigr)\) parameters and \(2\ell\) layers with probability at least \(1-\delta\).

Proof Idea 1/2

For any \(K\in [-1,1]^{d\times d\times c\times1}\) with \(\|K\|_{1}\leq1\) and \(X\in [0,1]^{D\times D\times c}\) we want to approximate \(K*X\) with \(V*\sigma(U*X)\) where \(U\) and \(V\) are tensors with i.i.d. \(\text{Uniform}(-1,1)\) entries.

Let \(U\) be \(d\times d \times c\times n\) and \(V\) be \(1\times 1 \times n \times 1\).

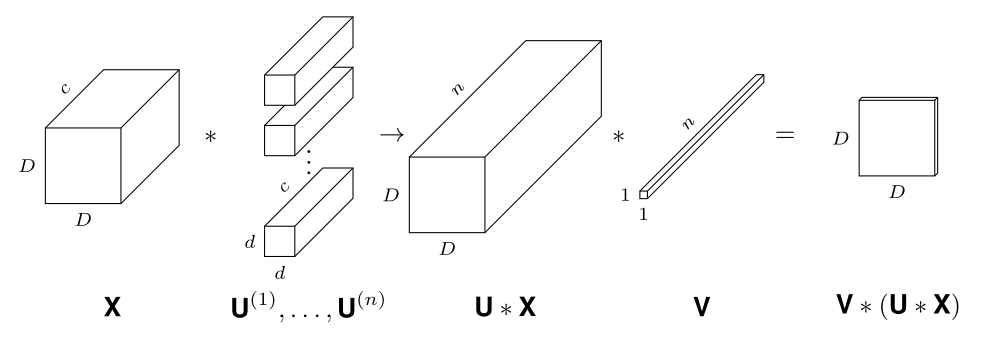
Proof Idea 2/2

\left(V*\left(U* X\right)\right)_{r,s,1} =\sum_{t=1}^{n}V_{1,1,t,1}\cdot\left(U* X\right)_{r,s,t}\\ =\sum_{t=1}^{n}V_{1,1,t,1}\cdot\left(\sum_{i,j\in\left[d\right],k\in\left[c\right]}U_{i,j,k,t}\cdot X_{r-i+1,s-j+1,k}\right)_{r,s,t}\\ =\sum_{t=1}^{n}\sum_{i,j\in\left[d\right],k\in\left[c\right]}\left(V_{1,1,t,1}\cdot U_{i,j,k,t}\right)\cdot X_{r-i+1,s-j+1,k}\\ =\sum_{i,j\in\left[d\right],k\in\left[c\right]}\left(\sum_{t=1}^{n}V_{1,1,t,1}\cdot U_{i,j,k,t}\right)\cdot X_{r-i+1,s-j+1,k}\\ =\sum_{i,j\in\left[d\right],k\in\left[c\right]}L_{i,j,k,1}\cdot X_{r-i+1,s-j+1,k}

where \(L_{i,j,k,1}=\sum_{t=1}^{n}V_{1,1,t,1}\cdot U_{i,j,k,t}\)

Prune negative entries of \(U\) so that \(\sigma(U*X)=U*X\).