On the Random
Subset Sum Problem
and Neural Networks
Emanuele Natale
jointly with
A. Da Cunha & L. Viennot
11 January 2023
Deep Learning on the Edge
Turing test (1950)
Today
1st AI winter (1974–1980)
2nd AI winter (1974–1980)
"A hand lifts a cup"
Use of GPUs in AI (2011)
Today, most AI heavy lifting is done in the cloud due to the concentration of large data sets and dedicated compute, especially when it comes to the training of machine learning (ML) models. But when it comes to the application of those models in real-world inferencing near the point where a decision is needed, a cloud-centric AI model struggles. [...] When time is of the essence, it makes sense to distribute the intelligence from the cloud to the edge.
Neural Network Pruning
Blalock et al. (2020): iterated magnitude pruning still SOTA compression technique.
train
train
prune
prune
train
The Lottery Ticket Hypothesis
Frankle & Carbin (ICLR 2019):
Large random networks contains sub-networks that reach comparable accuracy when trained
train
sparse random network
sparse
bad network
..., train&prune
train&prune, ...,
large random network
sparse good network
train
sparse "ticket" network
sparse
good network
rewind
The Strong LTH
Ramanujan et al. (CVPR 2020) find a good subnetwork without changing weights (train by pruning!)
A network with random weights contains sub-networks that can approximate any given sufficiently-smaller neural network (without training)
Proving the SLTH
Pensia et al. (NeurIPS 2020)
Find combination of random weights close to w
Malach et al. (ICML 2020)
Find random weight
close to w
SLTH and the Random Subset-Sum Problem
Find combination of random weights close to w:
Lueker '98: n=O(logϵ1)
RSSP. For which n does the following holds?
Given X1,...,Xn i.i.d. random variables, with prob. 1−ϵ for each z∈[−1,1] there is S⊆{1,...,n} such that z−ϵ≤i∈S∑Xi≤z+ϵ.
SLTH for Convolutional Neural Networks
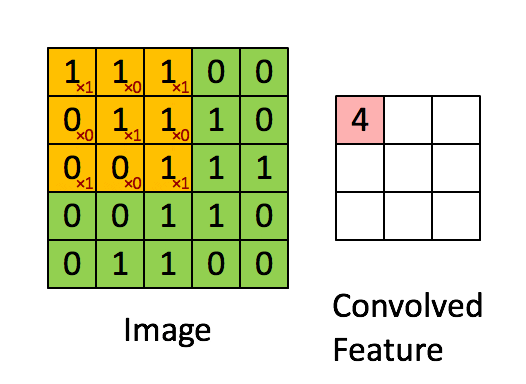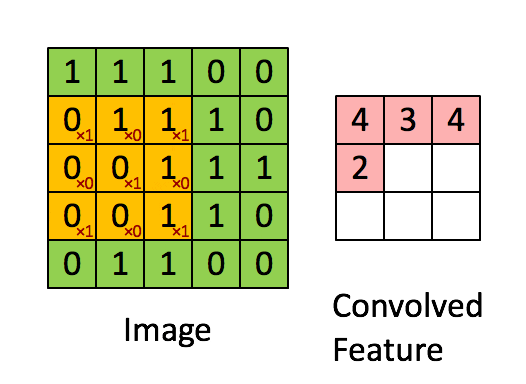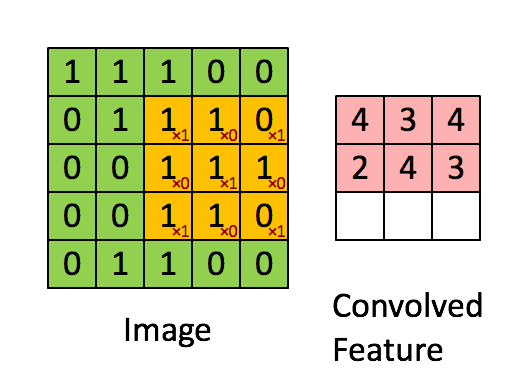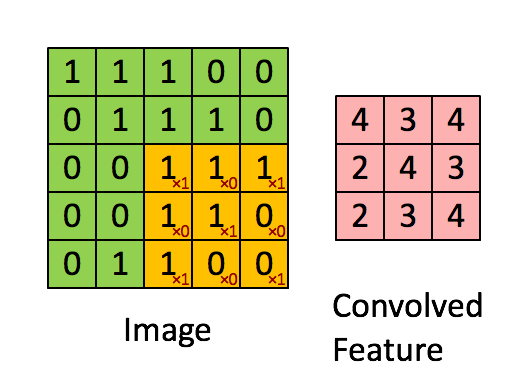
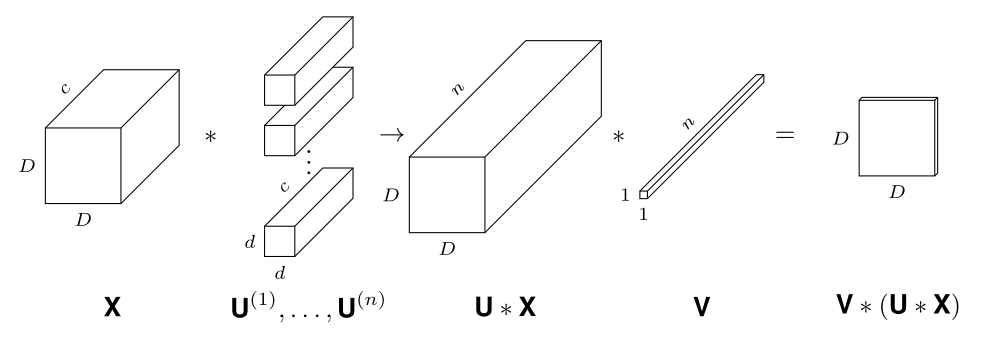
Theorem (da Cunha et al., ICLR 2022).
Given ϵ,δ>0, any CNN with k parameters and ℓ layers, and kernels with ℓ1 norm at most 1, can be approximated within error ϵ by pruning a random CNN with O(klogmin{ϵ,δ}kℓ) parameters and 2ℓ layers with probability at least 1−δ.
Reducing Energy: the Hardware Way
Resistive Crossbar Device
Analog MVM via crossbars of programmable resistances
Problem: Making precise programmable resistances is hard
Cfr. ~10k flops for digital 100x100 MVM
"Résistance équivalente modulable
à partir de résistances imprécises"
INRIA Patent deposit FR2210217
Leverage noise itself
to increase precision
RSS
Theorem
Programmable
effective resistance
Random Subset Sum Theory
bits of precision for any target value are linear w.r.t. number of resistances
Worst case among
2.5k instances