On the Random
Subset Sum Problem
and Neural Networks
Emanuele Natale
30 May 2023


Supported by
Academic Path
- 2017 - PhD in CS, Sapienza University
- 2014/15 - IRIF, Paris
- 2016, 2018 - Simons Institute for the Theory of Computing
- 2017-2018 - Max-Planck Institute for Informatics
- 2019 - COATI, INRIA d'Université Côte d'Azur

Research Interests


Best PhD + Young Resercher Prizes by It. Ch. EATCS
Computational Dynamics
Collaboration with

/CRONOS
Assembly Calculus

Ideas are sculpted in the brain by sparsifying it.
- L. Valiant
Neural Network Pruning
Blalock et al. (2020): iterated magnitude pruning still SOTA compression technique.
train
train
prune
prune
train
The Lottery Ticket Hypothesis
Frankle & Carbin (ICLR 2019):
Large random networks contains sub-networks that reach comparable accuracy when trained
train
sparse random network
sparse
bad network
..., train&prune
train&prune, ...,
large random network
sparse good network
train
sparse "ticket" network
sparse
good network
rewind
The Strong LTH
Ramanujan et al. (CVPR 2020) find a good subnetwork without changing weights (train by pruning!)
A network with random weights contains sub-networks that can approximate any given sufficiently-smaller neural network (without training)

Proving the SLTH
Pensia et al. (NeurIPS 2020)
Find combination of random weights close to \(w\)
Malach et al. (ICML 2020)
Find random weight
close to \(w\)
SLTH and the Random Subset-Sum Problem
Find combination of random weights close to \(w\):
RSSP. For which \(n\) does the following holds?
Given \(X_1,...,X_n\) i.i.d. random variables, with prob. \(1-\epsilon\) for each \(z\in [-1,1]\) there is \(S\subseteq\{1,...,n\}\) such that \[z-\epsilon\leq\sum_{i\in S} X_i \leq z+\epsilon.\]
Lueker '98: \(n=O(\log \frac 1{\epsilon})\)
Deep connection with integer linear programs
[Dyer & Frieze '89,
Borst et al. '22]
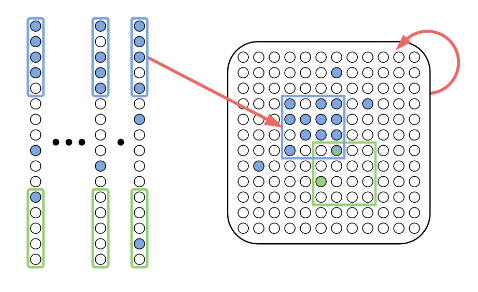
SLTH for Convolutional Neural Networks
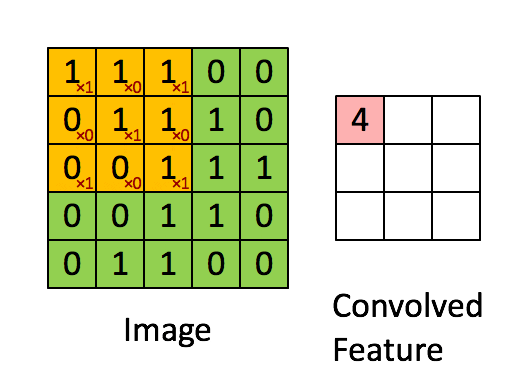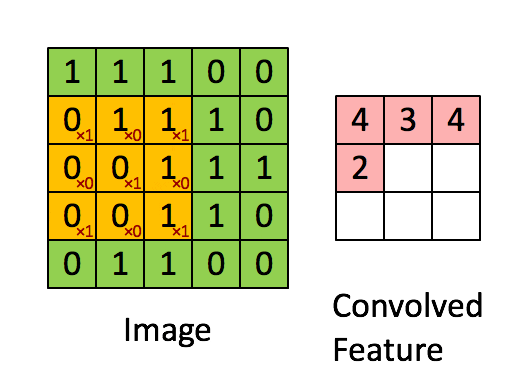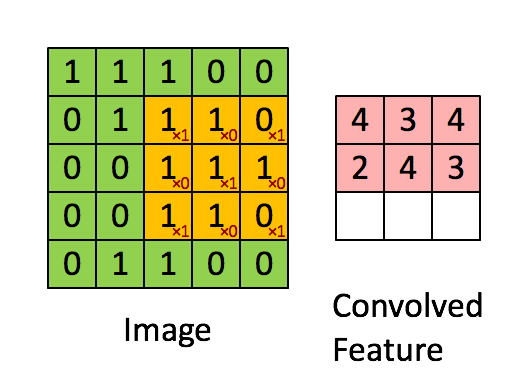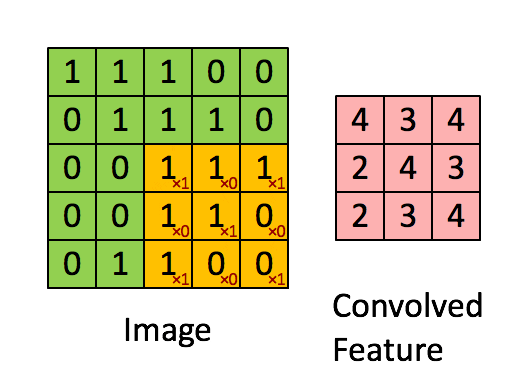
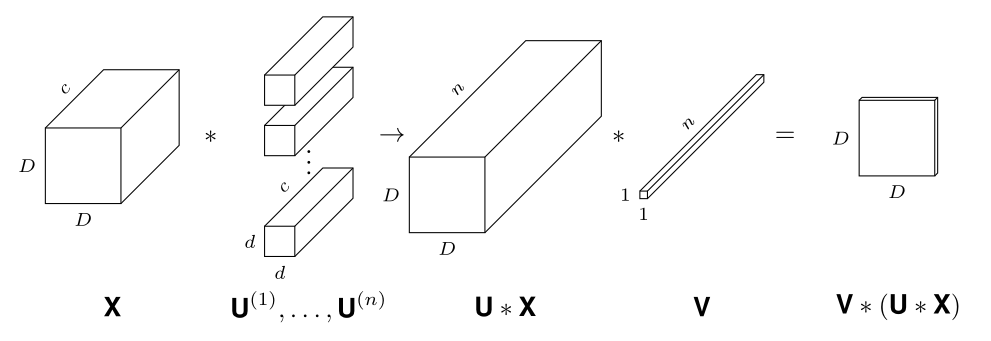
Theorem (da Cunha et al., ICLR 2022).
Given \(\epsilon,\delta>0\), any CNN with \(k\) parameters and \(\ell\) layers, and kernels with \(\ell_1\) norm at most 1, can be approximated within error \(\epsilon\) by pruning a random CNN with \(O\bigl(k\log \frac{k\ell}{\min\{\epsilon,\delta\}}\bigr)\) parameters and \(2\ell\) layers with probability at least \(1-\delta\).