Applications of Artificial Intelligence to Computational Chemistry

Nicholas J. Browning

Supervisor: Prof. Dr. Ursula Roethlisberger

  • Introduction
     
  • Motivation
     
  • EVOLVE
     
  • GAML
     
  • ML-MTS

Overview

1

Science, 2018, 361, 6400, pp. 360-365

Chemical Design

2

Chemical Space

Space defined by all possible molecules given a set of construction rules and boundary conditions

Chemical spaces are vast

J. Am. Chem. Soc., 2009, 131, 25, pp 8732–8733

ACS Chem Neurosci., 2012, 3, 9, pp 649–657.

3

> 10^{60}

Chemical Accuracy

Full CI

HF

DFT

MP2

Computational Cost

Accuracy

CC

\text{Experiment}
\infin

4

Motivating Remarks

 Designing new compounds with interesting properties requires searching incomprehensibly large chemical spaces

Requiring chemical accuracy for predicted properties engenders the use of computationally expensive electronic structure methods

5

1. Searching Chemical Space

2. Improving Chemical Accuracy, for Less

Evolutionary Algorithms

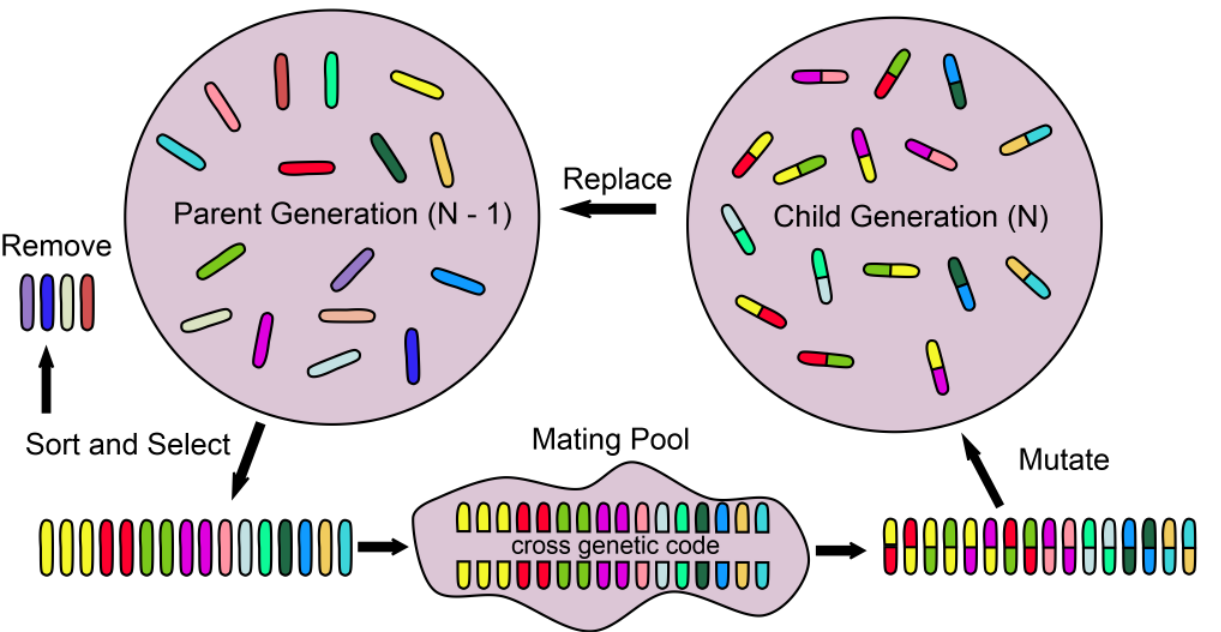
Optimisation algorithms inspired by biological processes or species behaviour

6

Particle Swarm Optimisation

Genetic Algorithms

Machine Learning

Replace expensive electronic structure calculation with cheaper, data-driven regression model

\left < \Psi| \hat H | \Psi \right >\rightarrow f(\{Z, R\})

7

Motivating Remarks

8

1. Searching Chemical Space

2. Improving Chemical Accuracy, for Less

EVOLVE: An Evolutionary Toolbox for the Design of Peptides and Proteins

Nicholas J. Browning, Marta A. S. Perez, Elizabeth Brunk, Ursula Roethlisberger, in submission, JCTC, 2019.

  • Introduction
  • Motivation
  • EVOLVE
  • GAML
  • ML-MTS

 

Haemoglobin (PDB 1A3N)

  • DNA Signalling
  • Acid-base catalysis
  • atom/group transfer
  • Electron transfer
  • Redox catalysis

Design of proteins is attractive:

  • Tune or change activity
  • Improve solvent tolerance
  • Increase thermal stability

Proteins fulfill a wide scope of biological functions ranging from regulation to catalytic activity:

Protein Design

Issues:

  • Search space is large
  • E.g 50-residue protein:

 

20^{50} \approx 1 \times 10^{65}

possible sequences

9

Short 20-mer polyalanine

Central 8 residues open to mutation (purple spheres)

EVOLVE Algorithm and Prototype

Side chain dihedrals discretised into set of 177 low-energy conformers [1]

1. Proteins, 2000, 40, pp 389-408

10

\vec{\chi} = \{\chi_i\}
f = \Delta E^\text{mutant}_{\text{system}} - \Delta E^{\text{ref}}_\text{system} = E^\text{mutant}_\text{system} - E^\text{ref}_\text{system} + \sum_i^N (E^{\text{ref}}_\text{aa}(i) - E^{\text{mutant}}_\text{aa}(i))
E_\text{system} = E^{FF99SB}_\text{system} + \Delta G^{GB}_{sol}

Amber FF99SB force field


Solvent effects modelled by implicit solvent model

Backbone stability measure

\epsilon = 80
\epsilon = 5 0
\epsilon = 10

Buried Protein Environment

Solvent Exposed

Intermediary

EVOLVE Fitness Function

11

94 Rotamers

177 Rotamers

177 Rotamers

-40.6 kcal/mol

-28.4 kcal/mol

-42.3 kcal/mol

EVOLVE Optimisation Curves

12

Fittest Individuals - Hydrophobic Environment

94 Rotamers

f = -28.4 kcal/mol

Buried Core Protein

13

Solvent Exposed Environment

Fittest Individuals - Solvent Exposed Environment

14

177 Rotamers

f = -40.6 kcal/mol

Homohelix Study

-40.6 kcal/mol

-28.4 kcal/mol

-42.3 kcal/mol

-28.1 kcal/mol

-28.0 kcal/mol

-27.9 kcal/mol

W04

15

Selection probabilities show consistent convergence towards a subset of chemical space

Selection Probabilities

16

Can use this subset to focus GA exploration on more interesting regions

55 Rotamer subset of residues: TRP, GLU, ASP, HIP, ARG

New fitness: -42.4 kcal/mol

Subspace Search

17

Outlook

J. Am. Chem. Soc., 2018, 140, 13, pp 4517–4521

Mutant protein solvent and pH tolerant

 

Thermostability greatly increased compared to wild-type

B1 Domain Protein G

18

1. Searching Chemical Space

2. Improving Chemical Accuracy, for Less

Genetic Optimisation of Training Sets for Improved Machine Learning Models of Molecular Properties

Nicholas J. Browning, Raghu Ramakrishnan, O. Anatole von Lilienfeld, Ursula Roethlisberger, JPCL, 2017

  • Introduction
  • Motivation
  • EVOLVE
  • GAML
  • ML-MTS

 

  • Can the error be improved by intelligent sampling - is less more?

  • Are there systematic trends in “optimal” training sets?

Chemical Interpolation

19

Chemical Database

8 heavy-atom subset of the QM-9 database [2]

10 thermochemical and electronic properties computed with DFT/B3LYP

2. Sci. Data, 2014, 1.

Out-of-sample test error used as fitness metric

Complex optimisation problem:

Database QM-8

Kernel Ridge Regression

\approx 10^{1449}

C(10900, 1000)

20

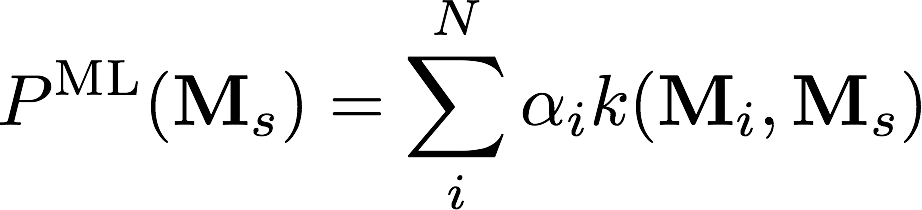
Significant reduction in out-of-sample errors

 

Fewer training molecules required to reach given accuracy

random sampling

GA optimised

Learning Curves - Enthalpy of Atomisation

21

Direct Learning

Delta Learning

Systematic Trends - Moments of Inertia

22

Certain molecules are more representative

Systematic shifts in distance, property, and shape distributions

Systematic Trends - Property Distributions

23

Certain molecules are more representative

Systematic shifts in distance, property, and shape distributions

Motivating Remarks

1. Searching Chemical Space

2. Improving Chemical Accuracy, for Less

24

Machine Learning Enhanced Multiple Time Step Ab Initio Molecular Dynamics

Nicholas J. Browning, Pablo Baudin, Elisa Liberatore, Ursula Roethlisberger

  • Introduction
  • Motivation
  • EVOLVE
  • GAML
  • ML-MTS

 

Molecular Dynamics

Provides a 'window' into the microscopic motion of atoms in a system

F_A = -\nabla_A E_0(\{R, r\})

Forces acting on (classical) nuclei calculated from a potential energy surface

25

Key Issues
 

  • the accuracy of the potential energy surface : ML
  • timestep used to integrate atomic forces : MTS 

Multiple Time Step Integrators

Address the time step issue by observing that the forces acting on a system have different timescales

 

 

 

 

Separate "fast" and "slow" components of the total force, which can be integrated using smaller and larger timesteps

 

 

 

 

Slow forces typically expensive to compute therefore MTS yields a computational gain

26

MTS Algorithm

\gamma = (q_1, q_2, \dots, q_N, p_1, p_2, \dots, p_N)
iL = iL_\text{fast} + iL_\text{slow}
a(\gamma_t) = e^{iLt}a(\gamma_0)
e^{iL\Delta t} \approx e^{iL_{slow} \frac{\Delta t}{2}} \times e^{iL_\text{fast}\Delta t} (\Delta t) \times e^{iL_{slow} \frac{\Delta t}{2}}
e^{iL\Delta t} \approx e^{iL^\text{slow} (\Delta t/2)} \Big[ e^{iL^\text{fast} (\Delta t/n)} \Big]^n e^{iL^\text{slow} (\Delta t/2)}

Propagatation of phase space vector

Separate slow and fast components

phase space vector

Discrete time propagator obtained from Trotter factorisation

# initialise x, p
dt = 0.36
Dt = dt*n
Fslow = compute_slow_forces(x)
Ffast = compute_fast_forces(x)

for t in range(0, total_time, Dt): 
  p = p + 0.5*Dt*Fslow # Integrate slow components

  for i in range(1, n):  # Integrate fast components
    p = p + 0.5*dt*Ffast 
    x = x + dt * p/m
    Ffast = compute_fast_forces(x)
    p = p + 0.5*dt*Ffast

  Fslow = compute_slow_forces(x)
  p = p + 0.5*Dt*Fslow # Integrate slow components

27

\delta t

Ab Initio MTS

28

Machine Learning Potentials

Replace expensive electronic structure method with data-driven kernel model

 

Delta-learning model naturally results in an MTS scheme

F^\text{fast} = F^\text{low}
F^\text{slow} = \Delta F^\text{ML}
F^\text{fast} = F^\text{low} + \Delta F^\text{ML}
F^\text{slow} = F^\text{high} - F^\text{fast}

Scheme I ML-MTS

Scheme II ML-MTS

\Delta F^\text{ML} = F^\text{high} - F^\text{low}

Exact slow forces

Cost of high level, evaluated infrequently

Approximate slow forces

Cost of low level

29

\Delta E^\text{ML}(M_I) = E^\text{high}(M_I) - E^\text{low}(M_I) = \sum_I\sum_J k(M_I, M_J) \alpha_J
\Delta F_L^\text{ML}(M_I) = -\frac{\partial \Delta E^\text{ML}}{\partial R_L}(M_I) = -\sum_I\sum_J \frac{\partial k(M_I, M_J)}{\partial M_I} \frac{\partial M_I}{\partial R_L} \alpha_J

Use a computationally efficient kernel method [3]:

  • Generalisable
  • No 2nd derivatives required, only kernel and descriptor gradients
     

Representation:

  • ​​Atomic environments: Atomic Spectrum of London-Axilrod-Teller-Muto representation (aSLATM) [4]
     

MPI-ML code implemented into CPMD

Machine Learning Potentials

3. Chem. Phys., 2019, 150, 064105

4. ArXiv, 2017, https://arxiv.org/abs/1707.04146

30

Training Data

Trajectories of small isolated N-water molecule clusters

Fast components = LDA
Slow components = PBE0 -  LDA

Predictions made on liquid water

31

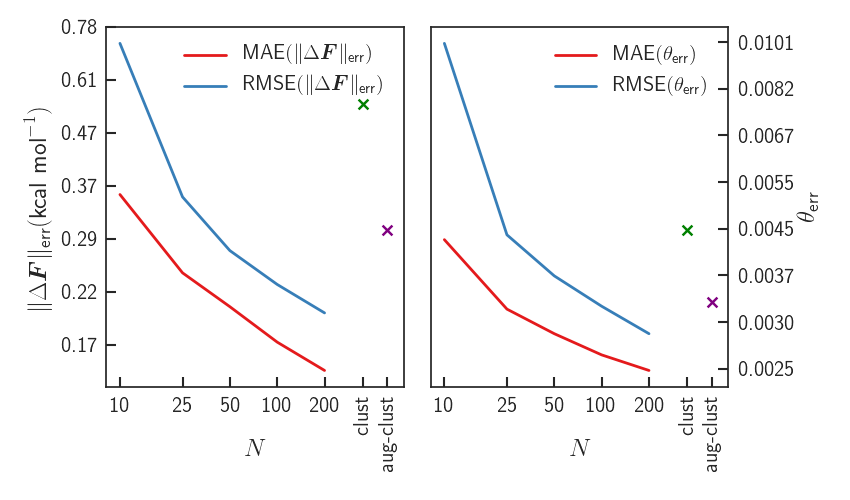
Results - Errors

32

Results - Errors

Significant improvement upon LDA - forces almost identical to PBE0

33

Results - Time Step and Speedup

Significant increase in outer timestep wrt. standard MTS


 

Resonance effects limit maximum outer timestep


 

Encouraging increase in overall speedup


Speedup dictated by number of SCF cycles to converge wfn

\epsilon = \frac{1}{N}\sum_i \frac{E_i - \bar{E}}{\bar E}

34

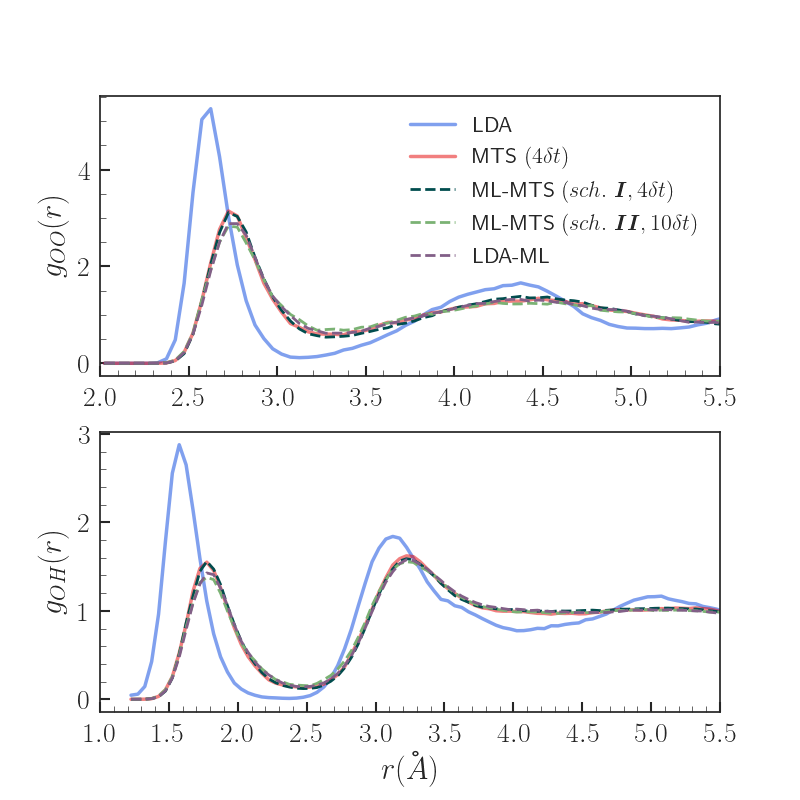
Results - Properties

MTS (n=4dt) identified as yielding properties with excellent agreement wrt. VV-PBE0 in previous work [5]

 

 

 

 

Both scheme I and II ML-MTS result in significantly improved radial distributions

5. J. Chem. Theory Comput., 2018, 14, 6, pp 2834–2842

35

1. Searching Chemical Space

Conclusions

  • EVOLVE is capable of searching through inordinately large chemical spaces
     
  • Meaningful chemical space insights can be gained from the EVOLVE procedure
     
  • Potential for experimental reach

36

2. Improving Chemical Accuracy, for Less

  • Within a specified chemical space, the accuracy of ML models can be significantly improved with intelligent sampling
     
  • kernel methods can provide a significant increase in timestep used in MTS integrators
    • ​Maintain good accuracy
    • Significantly reduce computational cost

Acknowledgements and Thanks

Dr. Raghu Ramakrishnan

Dr. Esra Bozkurt

Dr. Marta A. S. Perez

Dr. Pablo Baudin

Dr. Elisa Liberatore

Prof. Ursula Roethlisberger

37

Prof. O. Anatole von Lilienfeld

Prof. Clemence Corminboeuf

 Dr. Albert Bartók-Pártay

Dr. Ruud Hovius

Acknowledgements and Thanks

38

Thermostability Measure

f = \Delta E^\text{mutant}_{\text{system}} - \Delta E^{\text{ref}}_\text{system} = E^\text{mutant}_\text{system} - E^\text{ref}_\text{system} + \sum_i^N (E^{\text{ref}}_\text{aa}(i) - E^{\text{mutant}}_\text{aa}(i))
E_\text{system} = E^{FF99SB}_\text{system} + \Delta G^{GB}_{OBC}

Backbone stability measure

M. A. S. Perez, E. Bozkurt, N. J. Browning U. Roethlisberger, in preparation

39

Thermostability Measure

40

Manual Mutations

\epsilon = 80

D03-E05 -> R*-E05... =  -30.1 kcal/mol

-40.6 kcal/mol

-28.4 kcal/mol

-42.3 kcal/mol

D03-E05 -> E*-E05... =  -39.2 kcal/mol

\epsilon = 10

W04-W04-W04-W04-F04-Q05-W04 -> {8 x W*} =  -28.2 kcal/mol

41

EVOLVE: MOGA

42

Amino Acids

43

GA-ML Small Optimal Training Sets

44

GA-ML Distance Distributions

45

\boldsymbol{M}_I^{(2)}(r) = \frac{1}{2} \sum_{J\ne I} Z_IZ_J \frac{1}{\sigma_r \sqrt{2\pi} r^6} e^{-\frac{\left \lVert r - R_{IJ} \right \rVert ^2}{2\sigma_r^2}}
\boldsymbol{M}_I^{(3)}(\theta)= \frac{1}{3}\sum_{I \ne J \ne K} Z_I Z_J Z_K \frac{1}{\sigma_\theta \sqrt{2\pi}} e^{-\frac{\left ( \theta - \theta_{IJK} \right )^2}{2\sigma_\theta^2}} \frac{1 + \cos\theta \cos\theta_{JKI}\cos\theta_{KIJ}}{\left (R_{IJ} R_{IK} R_{KJ}\right)^3}
\boldsymbol{M}_I = \left \{ \boldsymbol{M}^{(1)}_I, \boldsymbol{M}^{(2)}_I, \boldsymbol{M}^{(3)}_I\right \}

SLATM Parameters

46

R_c = 4.8 A
\theta_\text{min} = -0.35 \ \text{rad}
\theta_\text{max} = 3.5 \ \text{rad}
\text{grid resolution}= 0.1A
\text{angular grid resolution}= 0.1 \ \text{rad}

Two-body term:

Three-body term:

\sigma_r = 0.05
\sigma_{\theta} = 0.05

Thermostability

47

Made with Slides.com