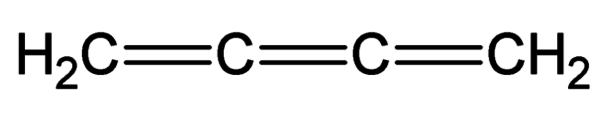Multi-configurational Time Dependant Hartree (MCTDH)
Nicholas J. Browning
Contents
-
Time Dependant Picture
-
Standard Method (SM)
-
Variational Principle (VP)
-
SM Equations of Motion (EoM)
-
Pitfalls of SM
-
-
Multi-configurational TDH (MCTDH)
- MCTDH EoM
- MCTDH Memory Requirements
- MCTDH Numerical Effort
- MCTDH Limitations
- MCTDH Mode Combination
- MCTDH Example
Time Dependant Picture
i\dot \Psi = H \Psi
(TI) orthonormal basis functions
Goal: derive equations of motion for coefficients
the Standard Method
nuclear coordinates or DoF
TD expansion coefficients
number of basis functions for DoF k
number of DoF
{\left\langle{\delta\Psi}\right |}H - i\frac{\delta}{\delta t}
{\left|{\Psi}\right\rangle} = 0
Variational Principle
\Psi \in \{\delta\Psi\}
\delta_tH = 0
Dirac-Frenkel Variational Principle
\langle \chi_{l_1} \ldots \chi_{l_f} | \sum\limits_{j_1 \ldots j_f} C_{j_1 \ldots j_f} H \chi_{j_1} \ldots \chi_{j_f} \rangle
=
i\langle \chi_{l_1} \ldots \chi_{l_f} | \sum\limits_{j_1 \ldots j_f} \dot C_{j_1 \ldots j_f}\chi_{j_1} \ldots \chi_{j_f} \rangle
\delta\Psi = \sum\limits_{l_1\ldots l_f}\frac{\delta\Psi}{\delta C_{l_1 \ldots l_f}}\delta C_{l_1 \ldots l_f}=\sum\limits_{l_1 \ldots l_f} \chi_{l_1}^{(1)}(q_1)\ldots \chi_{l_f}^{(f)}(q_f)\delta C_{l_1}\ldots l_f
\dot\Psi=\sum\limits_{j_1 \ldots j_f} \dot C_{j_1 \ldots j_f}(t) \chi_{j_1}^{(1)}(q_1)\ldots \chi_{j_f}^{(f)}(q_f)
\sum\limits_{j_1 \ldots j_f} \langle \chi_{l_1} \ldots \chi_{l_f} | H \chi_{j_1} \ldots \chi_{j_f} \rangle C_{j_1 \ldots j_f}
=
i \dot C_{j_1 \ldots j_f}
J=(j_1\ldots j_f)
\chi_J = \prod\limits_{\kappa=1}^f\chi_{j_\kappa}
i \dot C_{L} = \sum\limits_{J} \langle \chi_{L} | H| \chi_{J} \rangle C_{J}
SM Equations of Motion
Pitfalls of the Standard Method
Need at least 10 basis functions
per degree of freedom
10^f
coupled equations to be solved
f=3N-6 =12=10^{12}
E.g. 6 atom molecule
J=(j_1\ldots j_f)
\chi_J = \prod\limits_{\kappa=1}^f\chi_{j_\kappa}
i \dot C_{L} = \sum\limits_{J} \langle \chi_{L} | H |\chi_{J} \rangle C_{J}
Time Dependant Hartree (TDH)
constraints:
variation in
variation in
TDH EoM
choice of gk is arbitrary - simply shifts phase factors between a and \psi_k
TDH Pitfalls
20^{12}
12 \times 20
TDH reduces an f-dimensional PDE to a set of f one-dimensional PDEs
SM
TDH
visualisation of v - <v>
MCTDH
\Psi (q_1, \ldots, q_f, t) = \sum\limits_{j_1}^{n_1}\ldots\sum\limits_{j_f}^{n_f}A_{j_1 \ldots j_f}(t) \prod\limits_{k=1}^{f}\psi_{j_k}^{(k)}(q_k, t)
=\sum\limits_JA_J\Phi_J
\psi_{j_k}^{(k)}(q_k, t) = \sum\limits_{i_k=1}^{N_k}c_{i_kj_k}^{(k)}(t)\chi_{i_k}^{(k)}(q_k)
J=(j_1\ldots j_f)
MCTDH
\Psi_l^{(k)} = \langle\psi_l^{(k)}|\Psi\rangle = \sum\limits_{J^k}A_{J_l^k}\prod\limits_{v\ne k}\psi_{j_v}^{(v)}
\Psi (q_1, \ldots, q_f, t) = \sum\limits_JA_J\Phi_J =\sum\limits_{j=1}^{n_k}\psi_j^{(k)}\Psi_j^{(k)}
\langle H \rangle_{jl}^{(k)} = \langle \Psi_j^{(k)}| H| \Psi_l^{(k)} \rangle
\rho_{jl}^{(k)} = \langle\Psi_j^{(k)}|\Psi_l^{(k)}\rangle = \sum\limits_{J^k}A_{J_j^k}^*A_{J_l^k}
P^{(k)} = \sum\limits_{j=1}^{n_k}|\psi_j^{(k)}\rangle\langle\psi_j^{(k)}|
DFVP
i\dot A_J = \sum\limits_L\langle\Phi_J|H|\Phi_L\rangle A_L- i\sum\limits_{k=1}^f\sum\limits_{l=1}^{n_k}g_{j_kl}^{(k)}A_{J^k_l}
i \dot {\mathbf{\psi}}^{(k)}= (\hat g^{(k)}\mathbf{1})\mathbf{\psi}^{(k)}+ (1 -P^{(k)})\{ (\mathbf{\rho}^{(k)})^{-1}\langle\mathbf H \rangle^{(k)} - \hat g ^{(k)} \mathbf{1}\}\mathbf{\psi}^{(k)}
i\dot A_J = \sum\limits_L\langle\Phi_J|H|\Phi_L\rangle A_L
i \dot {\mathbf{\psi}}^{(k)}=(1 -P^{(k)})\{h^{(k)} \mathbf{1} + (\mathbf{\rho}^{(k)})^{-1}\langle\mathbf H_R \rangle^{(k)} \}\mathbf{\psi}^{(k)}
H=\sum\limits_kh^{(k)} + H_R
\hat g^{(k)} \equiv 0
\mathbf{\psi}^{(k)}= (\psi_1^{(k)}, \ldots, \psi_{n_k}^{(k)})^T
MCTDH - Memory
| f | Standard Method | MCTDH | |||
|---|---|---|---|---|---|
| 3 | 1.54MB | 190KB | 343 | 672 | 32768 |
| 4 | 48MB | 620KB | 2401 | 896 | 1.05E+06 |
| 6 | 48GB | 22MB | 117E+03 | 1344 | 1.07E+09 |
| 9 | 1.54PB | 7.2GB | 40E+06 | 2016 | 3.5E+13 |
\text{mem}_{\text{St.Mthd}} = 3 \times N^f \times \text{complex16 bytes}
\text{mem}_{\text{MCTDH}}=12\times( n^f + fnN ) \times \text{complex16 bytes}
n=7, N=32
gain_{mem} = \frac {1}{4}(\frac{N}{n})^f
n^f
fnN
N^f
MCTDH - CPU EFFORT
\text{effort}_\text{St.Method} \approx c_0.f.N^{f+1}
gain_{CPU} = \frac{c_0}{c_2}\frac{1}{sf}(\frac{N}{n})^{f+1}
\text{effort}_\text{MCTDH} \approx c_1.s.f.n.N^2 + c_2.s.f^2.n^{f+1}
Limiting factor for both memory and CPU is A-vector length
MCTDH - Limitations
n^f
\text{mem}_{\text{MCTDH}}=12\times( n^f + fnN ) \times \text{complex16 bytes}
\text{effort}_\text{MCTDH} \approx c_1.s.f.n.N^2 + c_2.s.f^2.n^{f+1}
MCTDH - Mode Combination
Q_k\equiv(q_{k,1},q_{k,2 }, \ldots, q_{k, d})
\psi_j^{(k)}(Q_k, t)=\psi_j^{(k)}(q_{k,1},q_{k,2 }, \ldots, q_{k, d})
\Psi(Q_1, \ldots, Q_p, t) = \sum\limits_{j_1}^{n_1}\ldots\sum\limits_{j_p}^{n_p}A_{j_1 \ldots j_p}(t) \prod\limits_{k=1}^{p}\psi_{j_k}^{(k)}(Q_k, t)
\equiv\Psi (q_1, \ldots, q_f, t)
\psi_j^{(k)} (Q_k, t)=\sum\limits_{i_1\ldots i_d}C_{i_1\ldots i_d}^{(k,j)} \chi^{(k,1)}(q_{k, 1})\ldots\chi^{(k,d)}(q_{k, d})
MCTDH-MC Pictoral Representation
a) Standard method
b) MCTDH
c) MCTDH with Mode Combination
d) ML-MCTDH (3 layer)
e) ML-MCTDH (4 layer)
MCTDH Mode Combination - Memory
| f | St. Method | MCTDH | 2-mode MCTDH | 3-mode MCTDH |
|---|---|---|---|---|
| 2 | 48KB | 282KB | - | - |
| 4 | 48MB | 620KB | 6MB | - |
| 6 | 48GB | 22MB | 10MB | 290MB |
| 10 | 48PB | 51GB | 160MB | 310MB |
| 15 | - | - | 210GB |
|
| 18 | - | - | 7.38TB | 29.3GB |
\text{mem}_{\text{MCTDH-MC}} = 12\times( \tilde {n}^{p} + p\tilde{n}N^d ) \times \text{complex16 bytes}
\text{mem}_{\text{St.Mthd}} = 3 \times N^f \times \text{complex16 bytes}
\text{mem}_{\text{MCTDH}}=12\times( n^f + fnN ) \times \text{complex16 bytes}
\tilde {n}_2 = 15
\tilde {n}_3= 23
N=32
n = 7
Example: Butatriene PhotoIonisation
C. Cattarius, G. A. Worth, H. D. Meyer, L. S. Cederbaum, J. Chem. Phys, 115 (2001), 2088-2100.
18f, 2 electronic states
