Введение в информационный поиск

Лекция 5

Оценивание результатов поиска

nzhiltsov.github.io/IR-course/

Обзор

Компоненты оценивания
Меры оценивания
Статистическая значимость результатов
Подсчет со скользящим контролем
Инструменты оценивания: trec_eval, galago eval

Компоненты оценивания

Тестовая коллекция документов
Набор тестовых информационных потребностей
- Поисковые запросы
Набор оценок релевантности для пар "запрос-документ"
- Даются специально натренированными людьми (асессорами)
- Как правило, бинарные (релевантен/нерелевантен)
- Могут иметь градацию (нерелевантен/слабо релевантен/релевантен/сильно релевантен)

Пример интерфейса асессора

Инициативы для оценки поиска

Text REtrieval Conference (TREC), trec.nist.gov
Initiative for the Evaluation of XML Retrieval (INEX)
Conference and Labs of the Evaluation Forum (CLEF), www.clef-initiative.eu
РОМИП, romip.ru

Меры оценивания

Меры качества без учета ранжирования

Точность (precision):
Полнота (recall):
F-мера (F-measure):

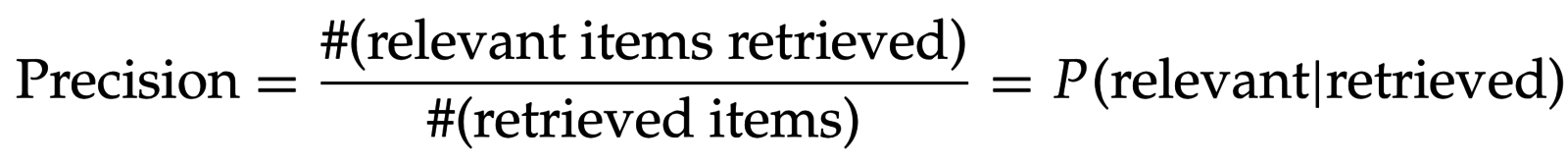
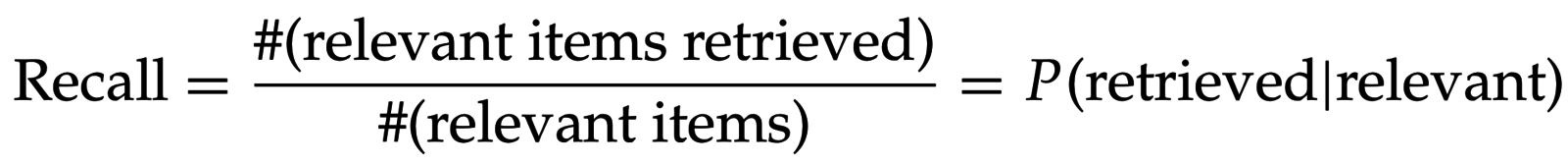
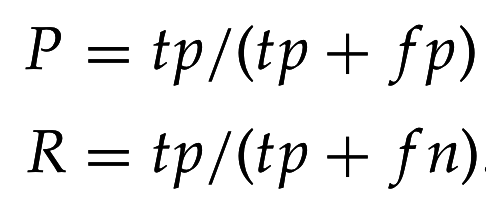
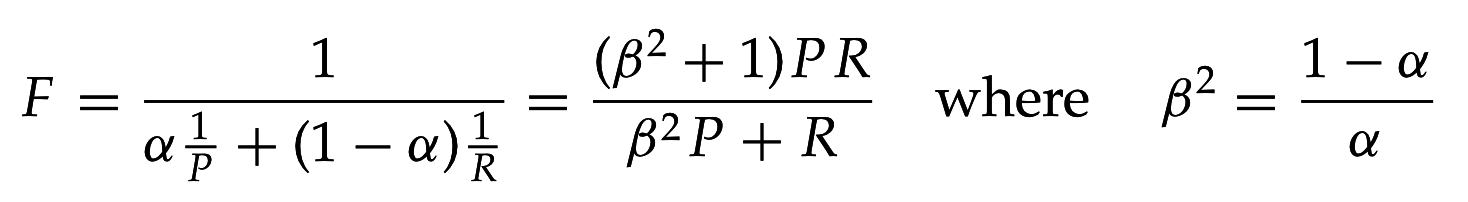
\alpha \in [0,1], \beta^2 \in [0,+\infty)

α \in [0, 1], β ​ 2 ​ ​ \in [0, + \infty)

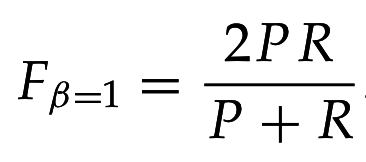
Кривая "точность-полнота"

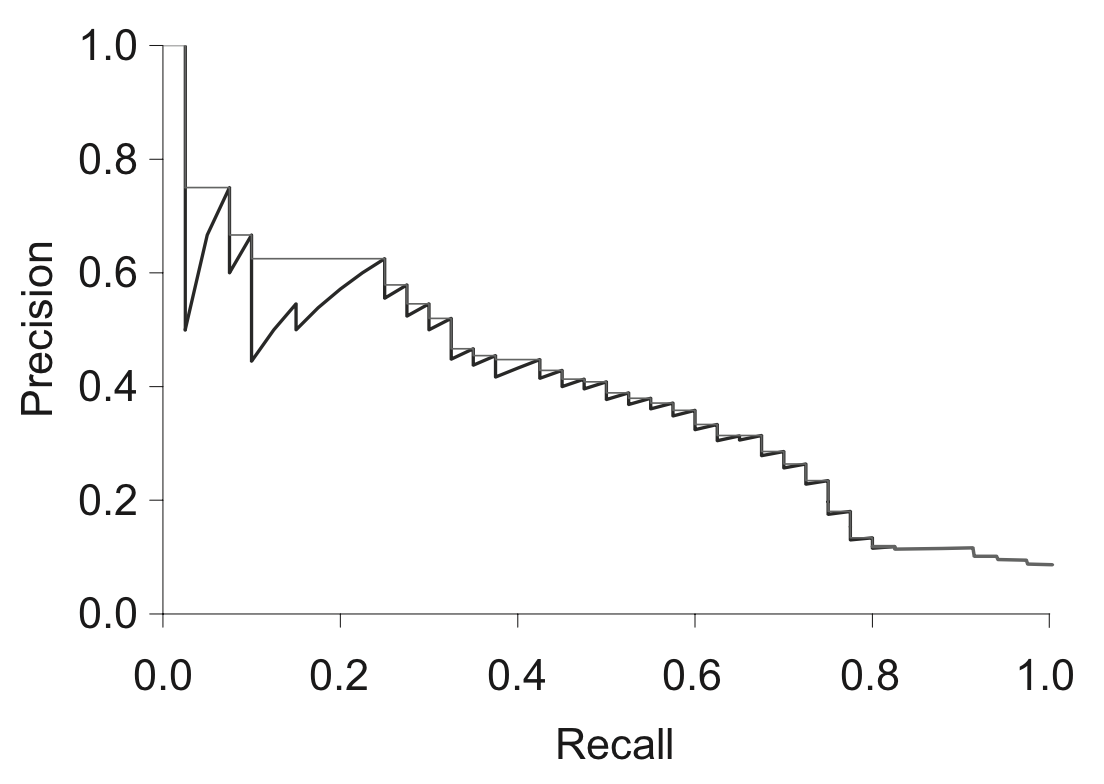
Строится для k первых документов, для разных k
Интерполированная точность для значений полноты :

r' \geq r

r ​' ​ ​ \geq r

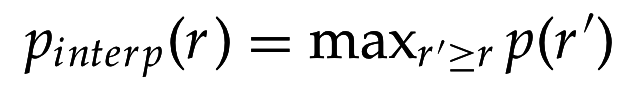
Средняя точность, интерполированная по 11 точкам

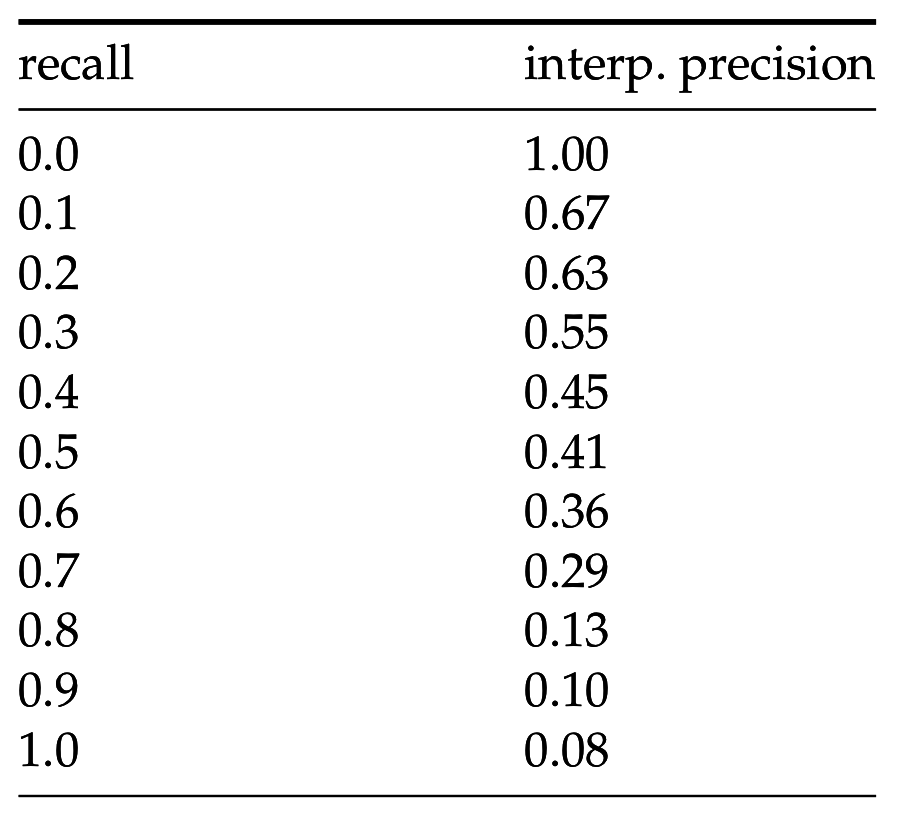
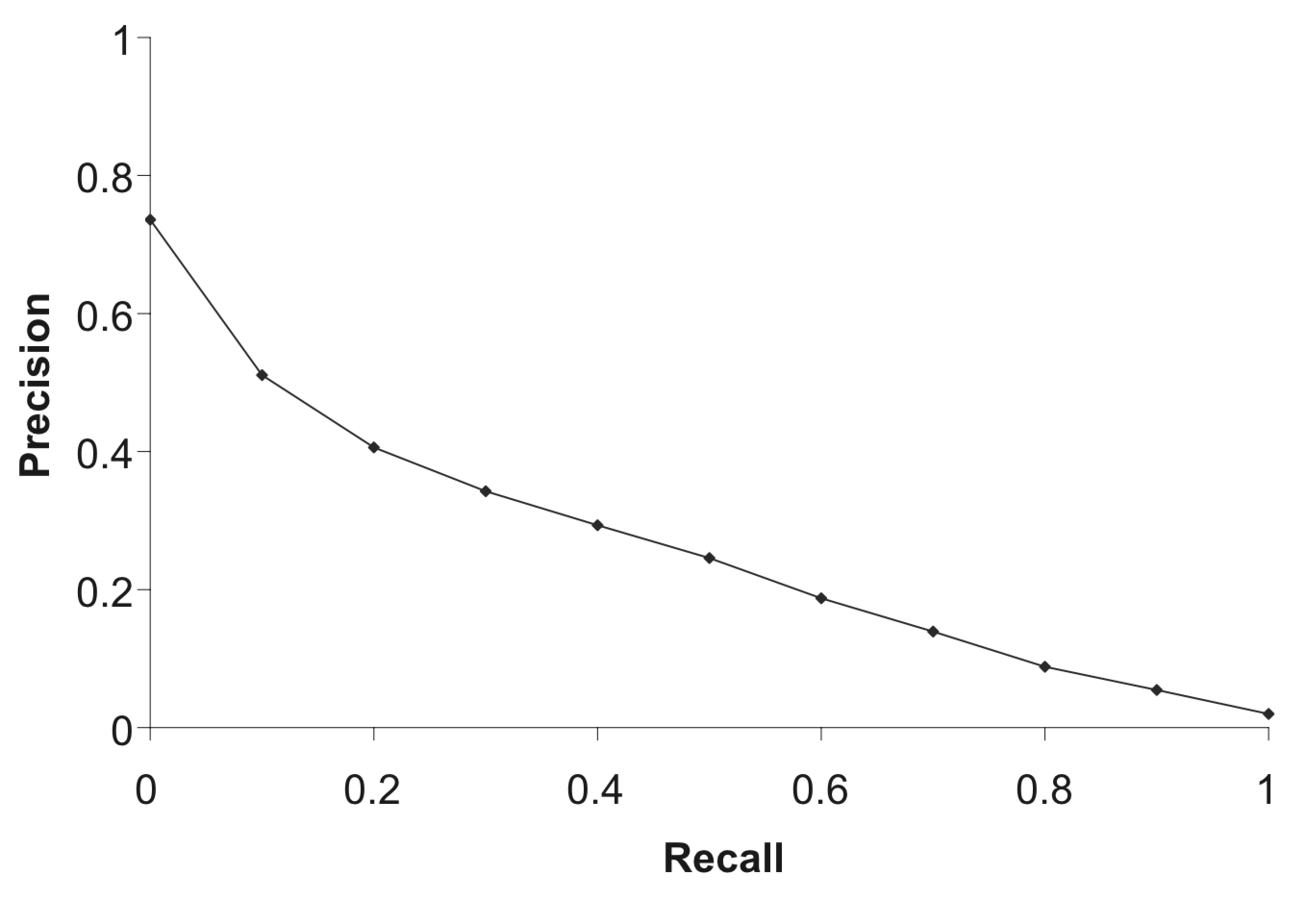
Для каждого запроса вычисляется
Для каждого уровня полноты вычисляется среднее арифметическое значение по всем запросам
Средняя точность (Average Precision)

p_{interp} (r), r \in \{0, 0.1, 0.2, ..., 1.0\}

p ​ i n t e r p ​ ​ (r), r \in {0, 0.1, 0.2, . . ., 1.0}

p_{interp}(r)

p ​ i n t e r p ​ ​ (r)

Макроусредненная средняя точность

Mean Average Precision (MAP)
Считаем значения точности на уровне очередного релеватного документа
Усредняем => средняя точность
Усредняем средние точности по всем запросам, нормируя по числу релевантных результатов:

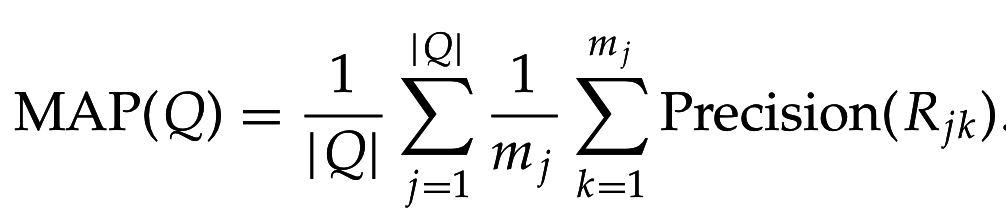
- релевантные документы для q
- множество top-k результатов
MAP - устойчивая мера качества и часто используется при оценке
MAP площадь под интерполированной кривой точность-полнота

d_1, ..., d_{m_j}

d ​ 1 ​ ​, . . ., d ​ m ​ j ​ ​ ​ ​

R_{jk}

R ​ j k ​ ​

\approx

\approx

Учет градации релевантности

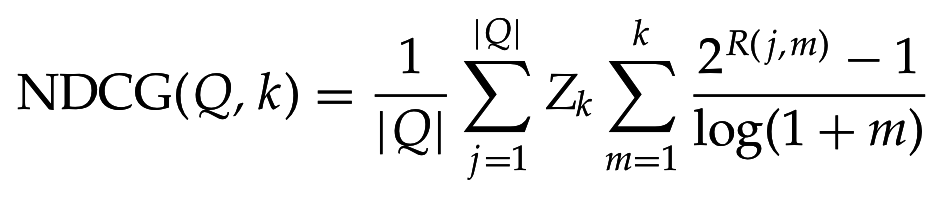
Нормированная дисконтированная совокупная выгода (normalized discounted cumulative gain, NDCG)
Считается на уровне top-k документов
- оценка релевантности документа d для запроса j
=> не учитывает позицию
=> "штраф" за низкий ранг
- оценка "идеального" DCG для данного запроса, то есть DCG(k), когда top-k документы отсортированы по
Усредняем по всем запросам => NDCG

R(j,d)

R (j, d)

Z_k

Z ​ k ​ ​

DCG(k)=\sum_{m=1}^k \frac{2^{R(j,m)}-1}{\log(1+m)}

D C G (k) = \sum ​ m = 1 ​ k ​ ​ \frac{​ 2 ​ R ( j , m ) ​ ​ - 1 ​ ​}{​ lo g ( 1 + m ) ​}

R(j,d)

R (j, d)

CG(k)=\sum_{m=1}^k 2^{R(j,m)}

C G (k) = \sum ​ m = 1 ​ k ​ ​ 2 ​ R (j, m) ​ ​

Mean Reciprocal Rank

MRR=\frac{1}{Q}\sum_{i=1}^{|Q|}\frac{1}{rank_i}

M R R = \frac{​ 1 ​ ​}{​ Q ​} \sum ​ i = 1 ​ ∣ Q ∣ ​ ​ \frac{​ 1 ​ ​}{​ r a n k ​ i ​ ​ ​}

Усредненный обратный ранг
- ранг первого релевантного документа
Усредняем обратные ранги по всем запросам => MRR
Широко применяется при оценке вопросно-ответного поиска (question answering, QA)

rank_i

r a n k ​ i ​ ​

Статистическая значимость

Статистическая значимость результатов поиска

Позволяет ответить на вопрос:
- значим ли прирост на X% по мере M для данного набора из Q запросов?
- либо прирост мог быть получен случайно
Используется аппарат математической статистики:
- тесты для проверки гипотез
На практике - если сложный метод не дает статистически значимый прирост по сравнению с основным простым методом (baseline) => лучше взять простой метод

Общий принцип проверки на статистическую значимость

Выбирается тестовая статистика, по которой нужны сравнить две поисковые системы
- Например, разность MAP
В качестве нулевой гипотезы предполагается, что между двумя системами нет разницы
Исследуем распределение тестовой статистики в предположении нулевой гипотезы
Вычисляем p-value, вероятность появления наблюдаемых значений тестовой статистики больше определенного уровня значимости (0.01;0.05)
Если значимость низка => отбрасываем нулевую гипотезу, иначе => системы не различаются

Тест Фишера (Fisher's Randomization Test)

Допустим системы A и B идентичны (нулевая гипотеза)
Разность MAP - тестовая статистика
Значит существует система N, которая генерирует результаты для запросов из Q и случайно помечает их то A, то B => способов
Любые перестановки меток равновероятны
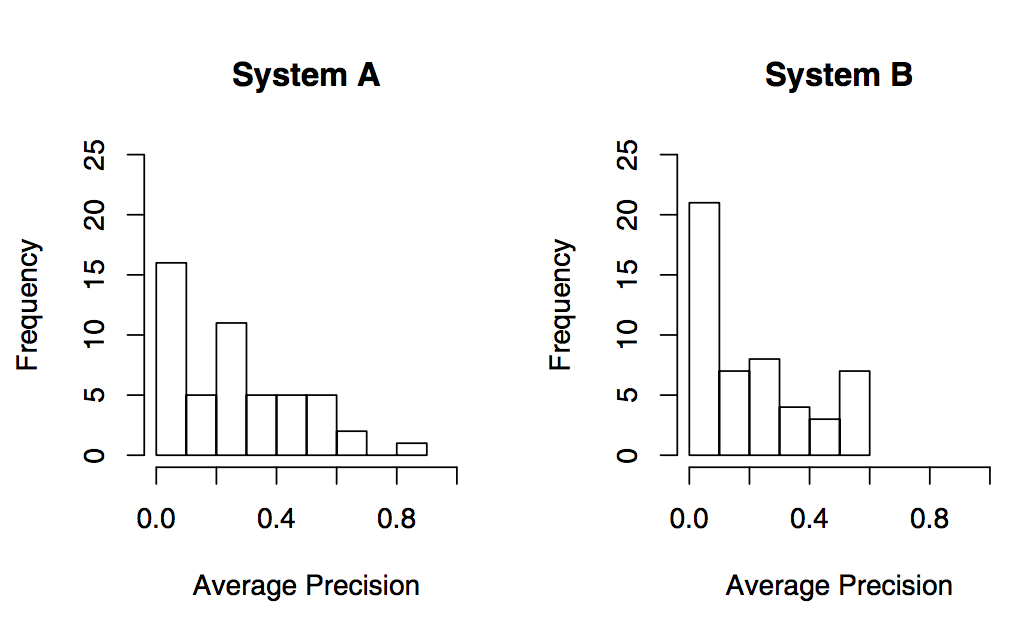
Одна из таких перестановок - наблюдаемая, пусть с результатом: MAP(A) = 0.258, MAP(B)=0.206
Считаем разность MAP на всевозможных перестановках
Считаем количество случаев S, когда разность MAP по модулю >= наблюдаемой 0.258-0.206=0.052
p-value (two-sided)
Обычно слишком велико, рассматривают случайную выборку, напр.,

2^{Q}

2 ​ Q ​ ​

2^{Q}

2 ​ Q ​ ​

=\frac{S}{2^Q}

= \frac{​ S ​ ​}{​ 2 ​ Q ​ ​ ​}

2^{Q}

2 ​ Q ​ ​

10^5

1 0 ​ 5 ​ ​

Тест Фишера (Fisher's Randomization Test)

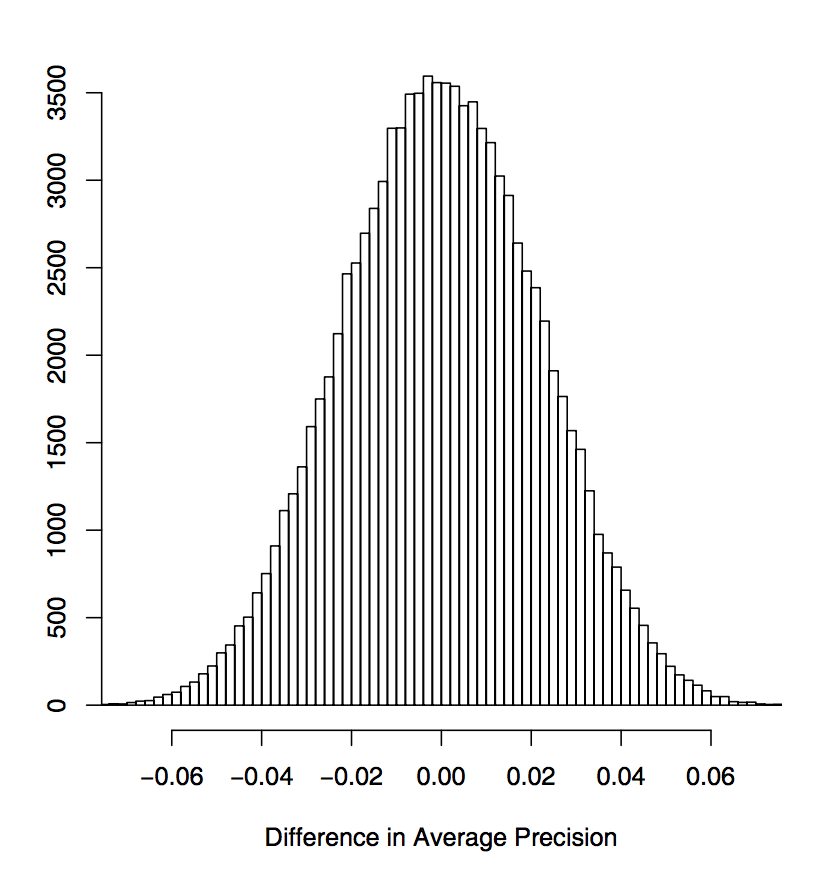
Разность MAP на перестановках

10^5

1 0 ​ 5 ​ ​

Наблюдаемые MAP

Пусть S=1380 => p-value=
Пусть уровень значимость p<0.05
=> c вероятностью (1-p)=95% можно отбросить нулевую гипотезу и признать, что система A статистически значимо лучше системы B

1380/10^5=0.0138

1380 / 1 0 ​ 5 ​ ​ = 0.0138

Подсчет со скользящим контролем

Мотивация

В некоторых функциях ранжирования есть параметры, для которых необходимо подобрать оптимальные значения для наилучших результатов
- параметры k1, b в BM25
- параметры сглаживания в языковых моделях
- машинное обучение ранжированию
Как корректно сравнить модели, требующие оптимизацию?
=> разделить множество поисковых запросов на два: 1) на котором оптимизируем (обучающее) и 2) на котором проверяем оптимизированную модель (контрольное, тестовое)
Уменьшение эффективного множества запросов для оценивания?

Схема блочного скользящего контроля

Случайно разбиваем множество запросов на k подмножеств
Оптимизируем параметры модели на объединении k-1 множеств по отношению к некоторой мере оценивания (напр., MAP)
Считаем меру оценивания на оставшемся i множестве
Повторяем k раз процедуру 1-3 для других
Усредняем результаты, полученные на 3 шаге

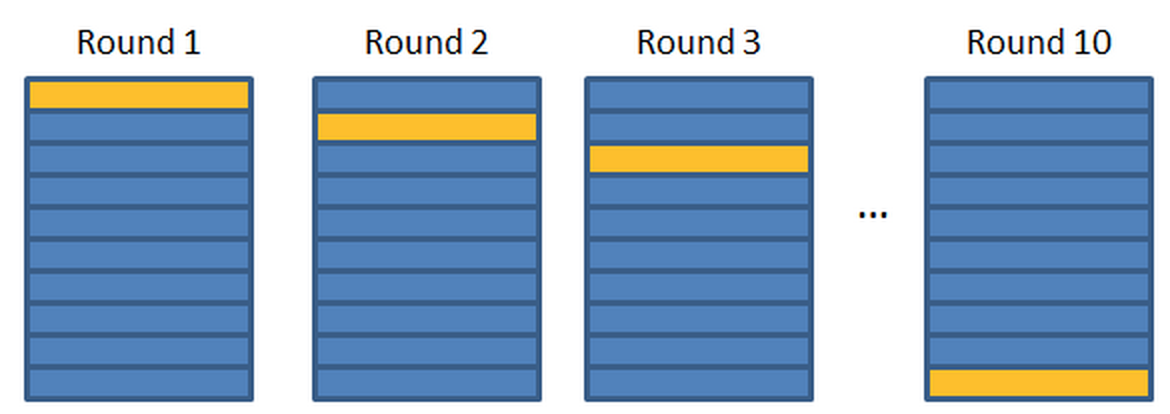
На практике обычно k=5 или k=10

i=\overline{1,k}

i = ​ 1, k ​ ​ ​

k-fold cross validation

Инструменты оценивания

trec_eval

Консольное приложение на C
Доступно на trec.nist.gov/trec_eval
Реализованы все основные меры оценивания поиска
Форматы файлов:

qrels

run

> trec_eval -q -c -m map qrels run

Galago Eval

Доступен как часть поисковой системы Galago (на Java): sourceforge.net/p/lemur/wiki/Galago
Функционал схож с trec_eval, те же форматы
Реализованы тесты статистической значимости (в т.ч. тест Фишера)
Пример команды:
- > bin/galago eval --judgments=qrels --runs+run1 --runs+run2 --metrics+map --metrics+P10

* означает значимость по тесту Фишера с p<0.05