Gränsvärden
\lim\limits_{x\to - 1} \frac{x^2+2x+1}{x+1}=0
\lim\limits_{x\to\infty} \frac{2x}{x-1}=2
y=3-2^{-x}
\lim\limits_{x\to\infty} \left(3-2^{-x}\right)=\lim\limits_{x\to\infty} \left(3-\frac{1}{2^x}\right)=3
Illustrerat gränsvärde
Bestäm eventuellt gränsvärde numeriskt
|
|
|
|---|---|
| -0,9 | 0,1 |
| -0,99 | 0,01 |
| -0,999 | 0,001 |
| -0,9999 | 0,0001 |
\lim\limits_{x\to - 1} \frac{x^2+2x+1}{x+1}
\frac{x^2+2x+1}{x+1}
x
Bestäm eventuellt gränsvärde numeriskt
\lim\limits_{x\to - 1} \frac{x^2+2x+1}{x+1}
\frac{x^2+2x+1}{x+1}
\lim\limits_{x\to - 1} \frac{x^2+2x+1}{x+1}=0
\lim\limits_{x\to 1} \frac{x^2+2x+1}{x-1}
|
|
|
|---|---|
| 0,9 | ≈ -36 |
| 0,99 | ≈ -396 |
| 0,999 | ≈ -3 996 |
| 0,9999 | ≈ -39 996 |
\frac{x^2+2x+1}{x-1}
Gränsvärde saknas!
x
x
|
|
|
|---|---|
| -1,1 | 0,1 |
| -1,01 | 0,01 |
| -1,001 | 0,001 |
| -1,0001 | 0,0001 |
\lim\limits_{x\to - 1} \frac{x^2+2x+1}{x+1}=
Bestäm eventuellt gränsvärde algebraiskt
=\lim\limits_{x\to - 1} \frac{(x+1)^2}{x+1}=
=\lim\limits_{x\to - 1} x+1=0
\lim\limits_{x\to\infty} \frac{2x}{x-1}=
=\lim\limits_{x\to\infty} \frac{2x-2+2}{x-1}=
=\lim\limits_{x\to\infty} \left(\frac{2x-2}{x-1}+\frac{2}{x-1}\right)=
=\lim\limits_{x\to\infty} \left(\frac{2(x-1)}{x-1}+\frac{2}{x-1}\right)=
=\lim\limits_{x\to\infty} \left(2+\frac{2}{x-1}\right)=2+0=2
Derivata
f'(x)
\frac{dy}{dx}
y'
D(f(x))
\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h}
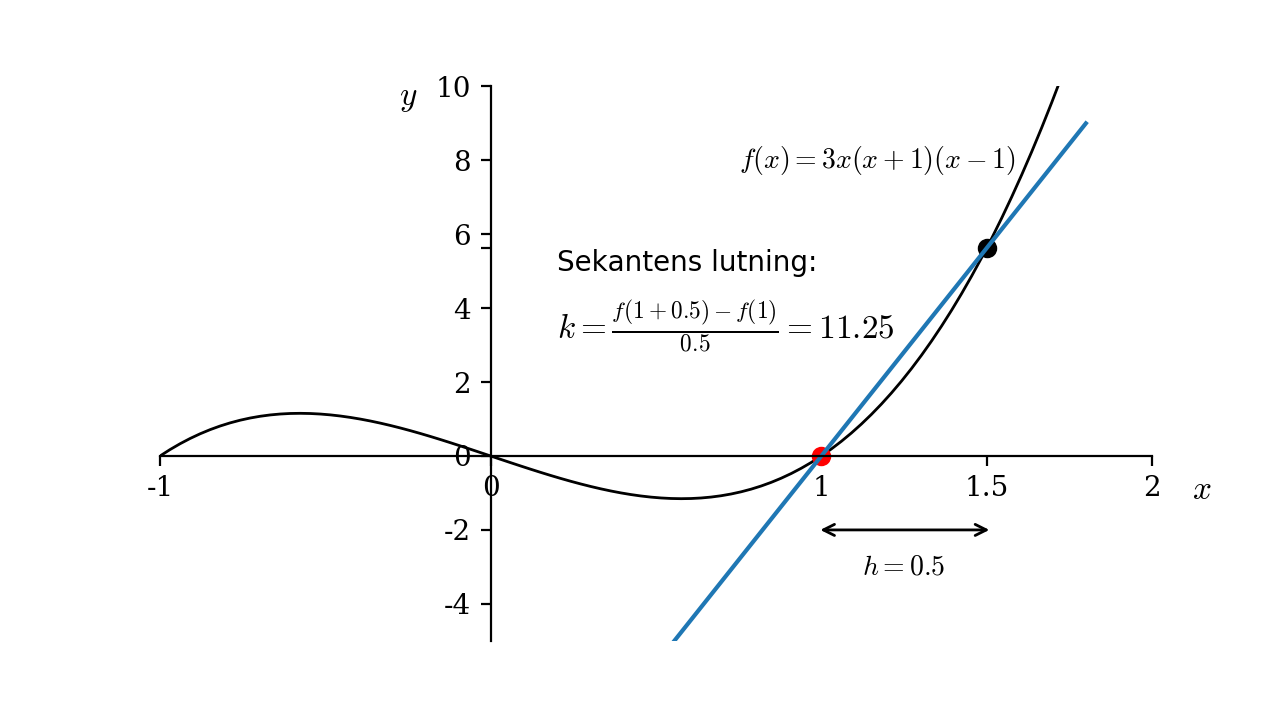
Sekantens lutning
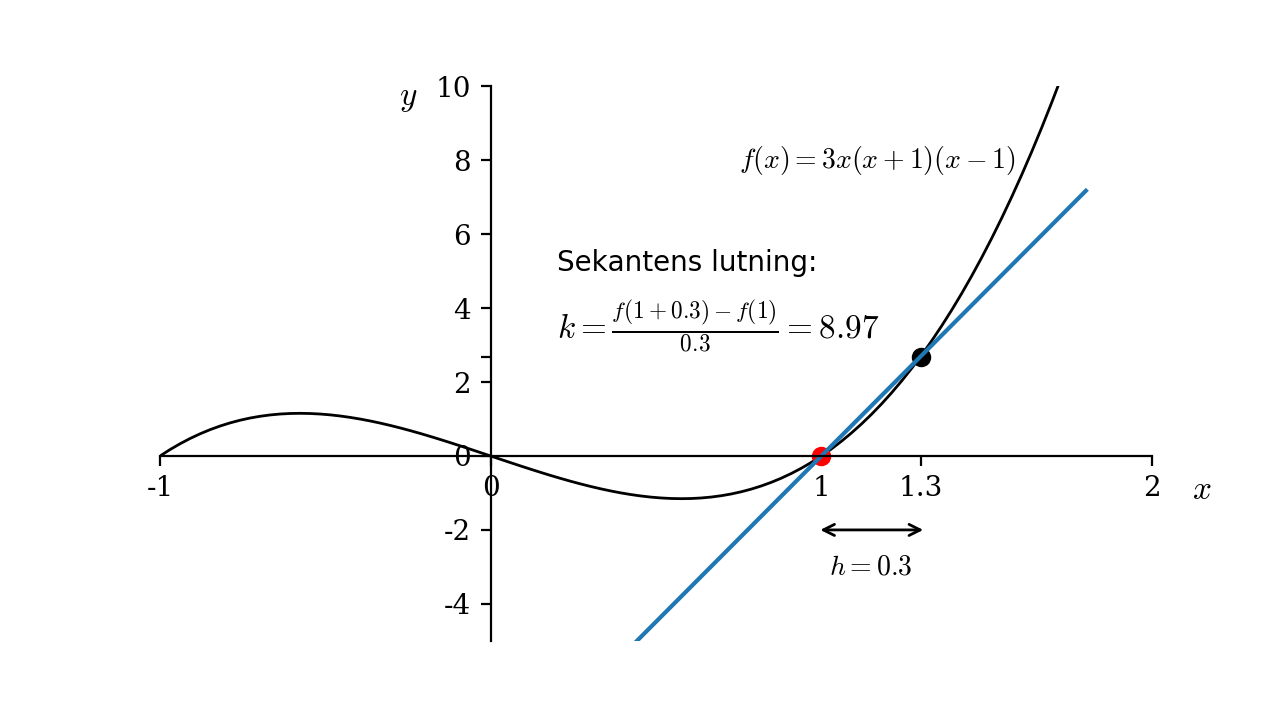
Sekantens lutning
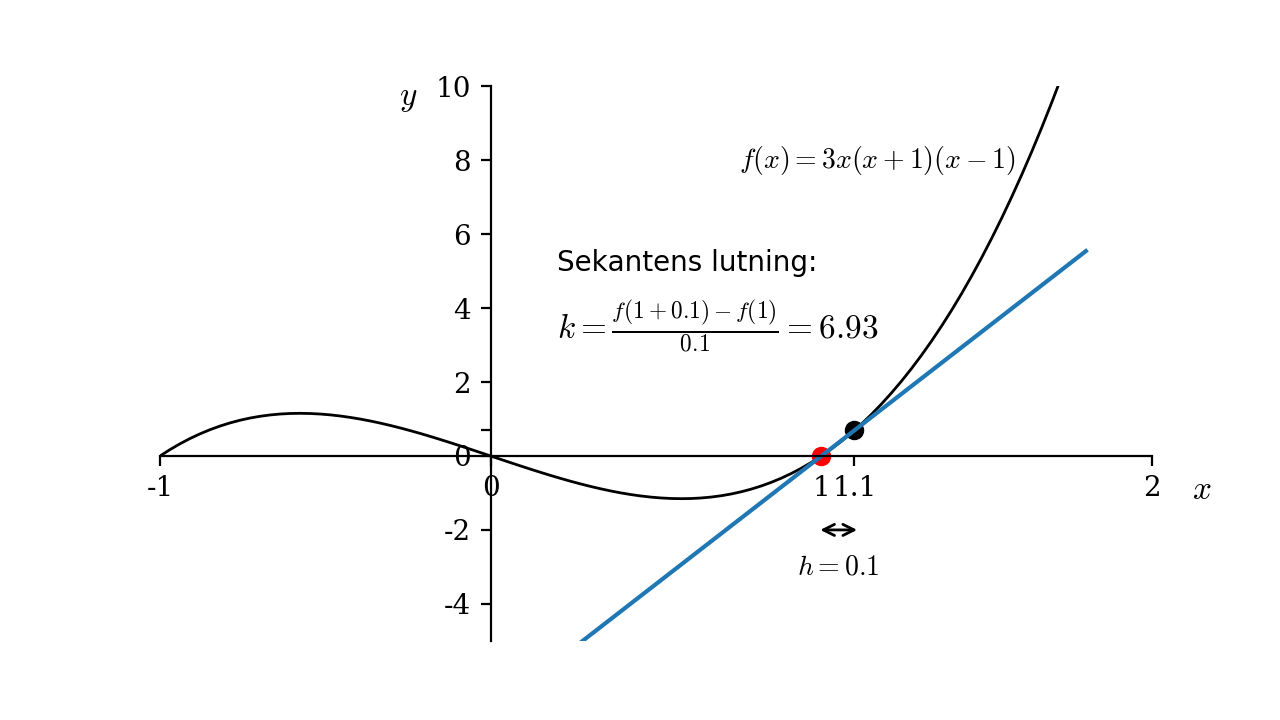
Sekantens lutning
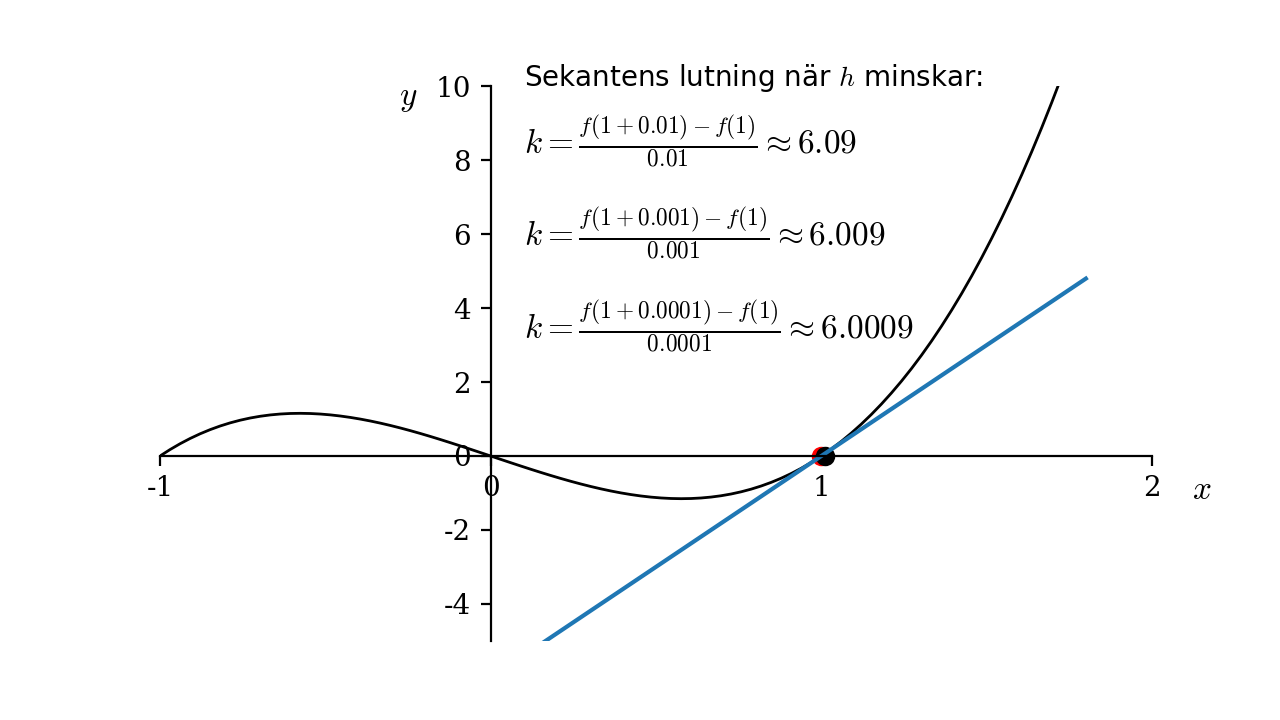
Sekantens lutning
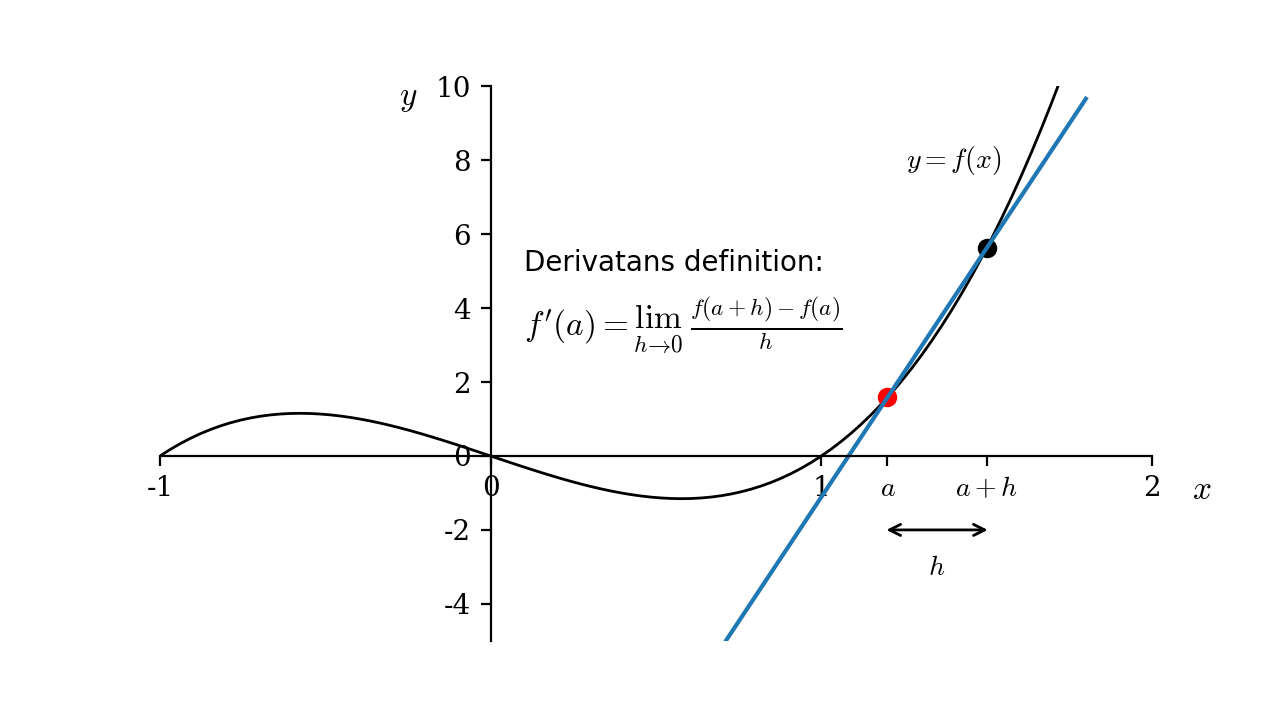
Derivatans definition
Exempel på tavlan
Låt \(f(x)=x^2\). Bestäm \(f'(-1)\)
Låt \(f(x)=3x+4\). Bestäm \(f'(2)\)