Talföljder och serier

Talföljder

Exempel på talföljder som definieras i en sluten formel

0,1,1,2,3,5,8,13,...

5, 7, 9, 11,...

a_1

a_2

a_3

a_4

a_n=a_1+d(n-1)=5+2(n-1)=3+2n

\text{(Detta gäller för \textbf{aritmetiska} följder)}

2, 10, 50, 250,...

a_n=a_1k^{n-1}=2\cdot 5^{n-1}

\text{(Detta gäller för \textbf{geometriska} följder)}

3,5,9,17,33,...

a_1=3

a_{n+1}=2a_n-1

a_1=0,a_2=1

a_{n+1}=a_{n-1}+a_n

5, 7, 9, 11,...

a_1=5

a_{n+1}=a_n+2

Exempel på talföljder som definieras i en rekursiv formel

a_1k^0

a_1k^2

a_1k^3

a_1k^1

Sierpinskis triangel

"Visuell rekursion", bygg ut mönstret efter samma regel.

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

Pascals triangel...

...modulo 2...

...blir en Sierpinskis triangel.

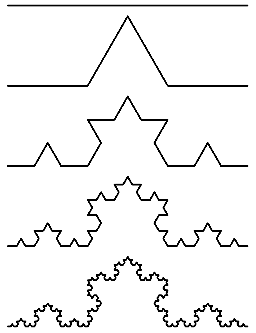
von Kochs kurva

von Kochs snöflinga

Aritmetiska serier

Vi utgår från en aritmetisk talföljd med fyra element och kallar dess summa .

s_4

s_4=5+10+15+20

s_4=20+15+10+5

2s_4=25+25+25+25=4\cdot(5+20)

s_4=\frac{4\cdot (5+20)}{2}

Allmänt:

s_n=\frac{n(a_1+a_n)}{2}

Detta kom den sedermera berömde matematikern Carl Friedrich Gauss på som ung skolpojke i slutet av 1700-talet. Klassen hade fått i uppgift att utföra additionen

1 + 2 + 3 + ... + 99 + 100. Gauss blev klar på någon minut med denna metod och var den enda i klassen som hade rätt.

Geometriska serier

Vi utgår från en geometrisk talföljd med fyra element och kallar dess summa .

s_4

s_4=ak^0+ak^1+ak^2+ak^3

\text{(exempel: 2, 4, 8, 16, $k=2$)}

ks_4=ak^1+ak^2+ak^3+ak^4

ks_4-s_4=ak^4-a

s_4(k-1)=a(k^4-1)

s_4=\frac{a(k^4-1)}{k-1}

Allmänt:

s_n=\frac{a_1(k^n-1)}{k-1}=\frac{a_1(1-k^n)}{1-k}

Summatecknet

2+10+50+250+1250 =\sum\limits_{k=1}^{5}2\cdot 5^{k-1}=\frac{2(5^5-1)}{5-1}

5+7+9+11+13=\sum\limits_{k=1}^{5}3+2k=\frac{n(a_1+a_n)}{2}

\Sigma

\frac{1}{3}+\frac{1}{9}+\frac{1}{27}+\frac{1}{81}+... =\sum\limits_{k=1}^{\infty}\frac{1}{3^k}=\lim\limits_{n\to\infty}\frac{\frac{1}{3}(\frac{1}{3^n}-1)}{\frac{1}{3}-1}=\lim\limits_{n\to\infty}\frac{\frac{1}{3}(1-\frac{1}{3^n})}{1-\frac{1}{3}}=\frac{1}{2}

a_n=a_1+d(n-1)

s_n=\frac{n(a_1+a_n)}{2}

a_n=a_1k^{n-1}

s_n=\frac{a_1(k^n-1)}{k-1}=\frac{a_1(1-k^n)}{1-k}

Tal i en aritmetisk talföljd:

Tal i en geometrisk talföljd:

Aritmetisk serie:

Geometrisk serie:

=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+...=1

\sum\limits_{n=1}^{\infty}\frac{1}{2^n}=

{enligt metod för oändlig serie i förra sliden}

En oändlig serie kan konvergera till ett tal

Tillämpningar på serier - virus

För en viss typ av virus gäller att de skapas lika många nya viruspartiklar per sekund som det fanns sekunden innan. Om det börjar med en viruspartikel, hur många finns det efter en minut?

1+2^0+2^1+2^2+2^3+2^4+...+2^{59}=1+\sum\limits_{k=0}^{59}2^k=1+\frac{2^0(2^{60}-1)}{2-1}=2^{60}

0 s 1 s 2 s 3 s 4 s

Efter fyra sekunder finns det 16 partiklar.

Tillämpningar på serier - spara pengar

Kajsa gör fem stycken årliga insättningar om 5 000 kr. Den årliga räntesatsen är på 10 %. Hur stort belopp har Kajsa direkt efter sista insättningen?

5000\cdot 1.1^4+5000\cdot 1.1^3+5000\cdot 1.1^2+5000\cdot 1.1^1+5000\cdot 1.1^0=

År 2010 2011 2012 2013

Pengar sätts in 1 januari varje år, ränta betalas ut den 31 december respektive år. De första 5 000 kronorna hinner förränta sig fyra gånger, de andra hinner förränta sig tre gånger osv. De sist insatta pengarna hinner inte förränta sig alls i situationen.

=5000\cdot( 1.1^0+1.1^1+1.1^2+ 1.1^3+1.1^4)=\frac{5000(1.1^5-1)}{1.1-1}\approx30\;525\text{ kr}

Tillämpningar på serier - annuitetslån

Kalle tar ett lån på 5 000 kr som ska återbetalas på fem år med fem lika stora belopp (annuiteter). Den årliga räntesatsen är på 10 %. Hur stor ska varje annuitet vara?

x\cdot 1.1^4+x\cdot 1.1^3+x\cdot 1.1^2+x\cdot 1.1^1+x\cdot 1.1^0=5\:000\cdot1.1^5

Om t ex lånet tas den 1 januari år 2010 så ska första annuiteten erläggas den 31 december samma år. Detta belopp ska växa med ränta på ränta för långivaren, varför ränta för de fyra kommande åren ska betalas.

Långivaren ser de utlånade pengarna som en investering som ska förränta sig varje år. För att få den beräknade räntan (här 10 %) så måste dock de pengar som erhålls från låntagarens annuiteter åter-investeras direkt, t ex genom mer utlån.

Termerna i ekvationens geometriska serie hanteras som i annuitetslånsexemplet i förra sliden.

När ekvationen löses erhålls annuiteten till 1 319 kr. Det ger totalbeloppet som återbetalas till 6 595 kr.

Tillämpningar på serier - nuvärde (1)

Kalle satte in ett belopp i en fond den 1 januari 2019 och band dem där i fem år. Fonden garanterade då att pengarna skulle växa med 5 % varje år, och Kalle räknade ut att han med sitt insatta belopp kan kassera in
100 000 den 31 december 2023.

Hur mycket pengar satte Kalle in i fonden?

x\cdot 1.05^5=100\ 000

x=\frac{100\;000}{1.05^5}\approx78\;353\text{ kr}

Pengarnas värde vid ett visst tillfälle under en tillväxt kallas nuvärde.

Tillämpningar på serier - nuvärde (2)

Lisa vann på en lott! Hon ska få 120 000 kr per år under fem års tid. Den första utbetalningen görs den 1 juli 2019. Hur mycket motsvarar hela vinstens värde vid den tidpunkten om man räknar med en räntetillväxt om 5 % per år?

\frac{120\;000}{1.05^4}+\frac{120\;000}{1.05^3}+\frac{120\;000}{1.05^2}+\frac{120\;000}{1.05^1}+\frac{120\;000}{1.05^0}=

Nuvärdet på de först utbetalda pengarna

Nuvärdet på de sist utbetalda pengarna

120\;000\cdot(\frac{1}{1.05^4}+\frac{1}{1.05^3}+\frac{1}{1.05^2}+\frac{1}{1.05^1}+\frac{1}{1.05^0})=

120\;000\cdot(1+\frac{1}{1.05^1}+\frac{1}{1.05^2}+\frac{1}{1.05^3}+\frac{1}{1.05^4})=\frac{120000\cdot((\frac{1}{1.05})^5-1)}{\frac{1}{1.05}-1}\approx545\;514\text{ kr}

Det innebär att om lotteriföretaget investerar så mycket pengar den 1 juli 2019 så täcker det utbetalningarna under alla fem åren.