Interferens i tunna skikt

Reflexion kan ge fasförskjutning

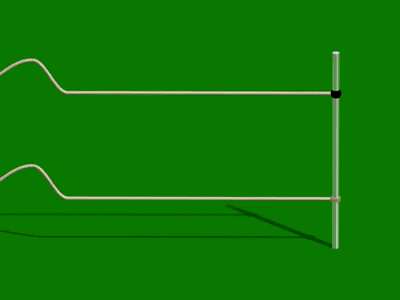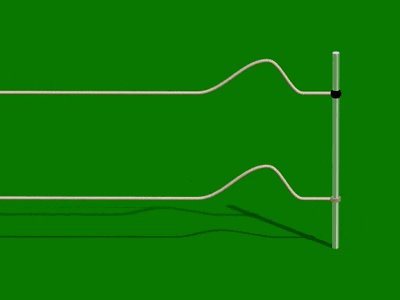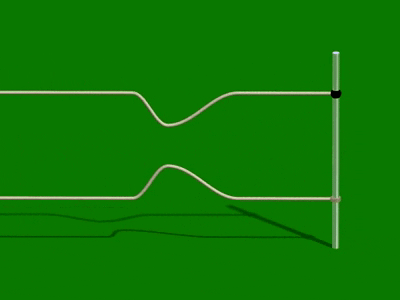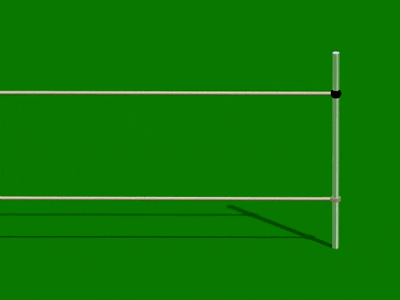
När en puls reflekteras mot en lös ändpunkt så kommer den tillbaka på samma sida.

Detta motsvaras av att ljus reflekteras mot ett medium där brytningsindex är lägre än därifrån strålen kommer.

När en puls reflekteras mot en fast änd-punkt så "vänds" den. Den är då fasför-skjuten i förhållande till den infallande vågen.

Motsvarande "vändning" sker då ljus reflekteras mot ett medium där brytnings-index är högre än därifrån strålen kommer.

Nikodemus Karlsson, fysikundervisning

Vågor fasförskjutna med \(\frac{\lambda}{2} \)

Fasförskjutning

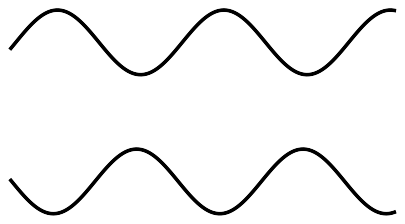
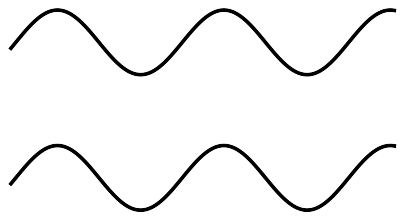
Vågor i fas

Nikodemus Karlsson, fysikundervisning

v_1=f\lambda_1

\frac{\lambda_1}{\lambda_2}=\frac{v_1}{v_2}=\frac{c/n_1}{c/n_2}=\frac{n_2}{n_1}

v_2=f\lambda_2

Om \(n_1=1\): \(\lambda_2=\frac{\lambda_1}{n_2} \)

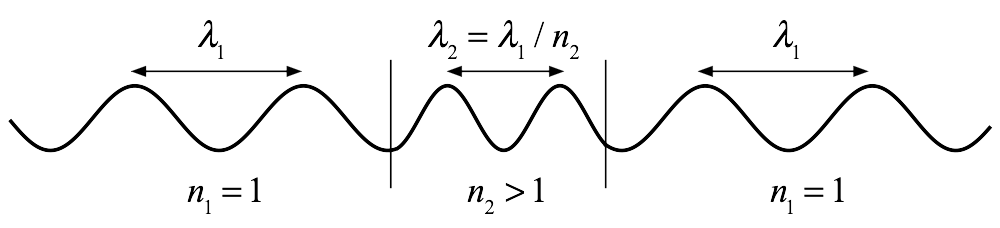
Våglängden varierar

Frekvensen konstant oavsett hastighet

För en given våglängd i luft kan våglängden i ett medium beräknas

Förhållandet mellanvåglängderna är det omvända mellan brytningsindex

Nikodemus Karlsson, fysikundervisning

Annat medium: n > 1

Luft: n = 1

Stråle 0

Stråle 1

Stråle 2

n=1

n>1

n=1

Referensstråle (fort-sättningen av opåver-kad Stråle 0)

Stråle 0

Stråle 2

Luft: n = 1

Stråle 0 reflekteras och fasförskjuts här!

Stråle 0

Stråle 1

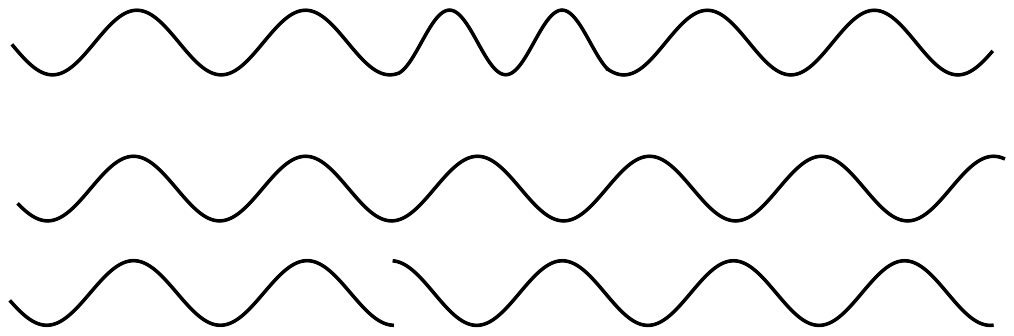
Påvisar hur vågorna kommit ur fas.

Optisk vägskillnad mellan Stråle 1 och 2 vid konstruktiv interferens: \(2nt\) eller \(\lambda (m+\frac{1}{2}) \), \(m=0, 1,2,...\)

Optisk vägskillnad vid vinkelrätt infall

Optisk vägskillnad mellan Stråle 1 och 2 vid destruktiv interferens: \(2nt\) eller \(\lambda m \), \(m=0, 1,2,...\)

Nikodemus Karlsson, fysikundervisning

Exempel

Såpa har brytningsindex 1.33. Vilka tjocklekar är möjliga för att att få konstruktiv interferens av våglängden 500 nm när vitt ljus reflekteras i en såpbubbla?

2nt=\lambda (m+\frac{1}{2})

t=\frac{\lambda(m+\frac{1}{2})}{2n}

m=0\Rightarrow t=0.0940\;\mu\text{m}

m=1\Rightarrow t=0.282\;\mu\text{m}

m=2\Rightarrow t=0.470\;\mu\text{m}

Och så vidare...

Nikodemus Karlsson, fysikundervisning

Annat medium: n > 1

Villkor för konstruktiv interferens

\Delta s = m\lambda,\;m=0,1,2...

\(\Delta s\) är optisk vägskillnad

\(\Delta s = 2nt\) vid vinkelrätt infall

Luft: n = 1

Stråle 0

Stråle 1

Stråle 2

Stråle 1 och 2 är dessutom fasförskjutna med \( \pi\) i förhållande till varandra.

Konstruktiv interferens med fasförskjutning / Destruktiv interferens utan fasförskjutning

Konstruktiv interferens utan fasförskjutning / Destruktiv interferens med fasförskjutning

2nt=\lambda(m+\frac{1}{2})

2nt=m\lambda

När ljuset faller in vinkelrätt

Luft: n = 1

Sammanfattning

Nikodemus Karlsson, fysikundervisning