1.10 Vectors and Matrices
What are they and why to we care about them ?

Vectors
What are they ?
(c) One Fourth Labs

- Start with simple x1, x2 axis (not x, y).
- Show a point in this 2-d plane.
- Now show an arrow from the origin to this point
- Now repeat the above for a few more points (such that one of these vectors is shorter than the first and the other is longer)
- Now in pink bubble write two bullet points: "Magnitude of a vector" and "Direction of a vector"
- Show formula for L2 norm (magnitude of the vector) and compute the magnitude of these vectors
- Now show two points in the x1,x2, plane (1,1) and (-1,1) and compute the magnitude (you can delete the other points). Both these points will be
Guiding principle for this entire lecture:
Many students in the course may be hearing the word "vector" for the first time. So we have to be very slow and methodically compute everything (even something as simple as L2 norm)
Vectors
What are they ? (some jargon)
(c) One Fourth Labs

- On RHS, write the definition if Euclidean space in a pink bubble
- On LHS top show a 2D Euclidean space with some points and their co-ordinates written
- On LHS bottom first show a 3D Euclidean space with some points and their co-ordinates written
- Now in pink bubble add L2 norm is also called Euclidean norm
Euclidean space, In geometry, a two- or three-dimensionalspace in which the axioms and postulates of Euclideangeometry apply; also, a space in any finite number of dimensions, in which points are designated by coordinates (one for each dimension) and the distance between two points is given by a distance formula
Vectors
How do you add, subtract, multiply vectors ?
(c) One Fourth Labs

Slide 1 (How do you add two vectors?)
- On LHS top show a 2D Euclidean space with two points and their co-ordinates written. On LHS write them as column vectors. Now add them and write the result. Now show the resulting vector on the Plot
- Repeat the above for 3d space
Slide 2 (How do you subtract one vector from another?)
- Repeat the above slide for subtraction
Slide 3 (How do you compute the dot product of two vectors?)
- LHS same as in the above two slides
- on RHS show the dot product formula for 2d and also show the column vectors
- Now show the formula in 3d and also show the column vectors
- For n-dimensions, show the formula
Slide 4 (How do you compute element-wise product of two vectors?)
- 2d, show formula \( \odot \), compute
- 3d, show formula \( \odot \), compute
- n-d, show formula
Vectors
How do you project a vector onto another ?
(c) One Fourth Labs

Slide1:
- Same as this video upto 4:09 seconds (but change the vectors a bit
https://www.youtube.com/watch?v=fqPiDICPkj8
- Now take a numeric example in 2d and compute
- Now take a numeric example in 3d and compute
- Now give formula for n-dimensions
Vectors
What is a unit vector ?
(c) One Fourth Labs

Slide1:
- Pink bubble "Any vector whose magnitude is 1?"
- Show the standard 0,1 and 1,0 vectors
- Show the 1/sqrt(2), 1/sqrt(2) vector
- Now show a non unit vector
- Now show how you get the unit vector in the direction of a vector
- repeat the same computation for one more vector (preferably with at least one -ve co-ordinate)
- Repeat the same for 3d space
Vectors
How do you compute the angle between two vectors ?
(c) One Fourth Labs

- 2d vector on LHS, cos formula on RHS, computations
- 3d vector on LHS, cos formula on RHS, computations
Vectors
What are orthogonal vectors?
(c) One Fourth Labs

Show cos formula on RHS
- Orthogonal --> perpendicular --> \theta = 90 --> cos = 0 --> cosine_formula = 0 --> dot product = 0
- Show examples of 2d orthogonal vectors. First show column vectors, then compute dot product, show it is 0, then show the vectors on the plot to convey that they are indeed 0.
- Repeat point 2 with examples in 3d
- Now show one example in 5d (its okay if you need to spread this across more than 1 slide)
Vectors
Why do we care about them ?
(c) One Fourth Labs

- Show an icon of a mobile phone. Now adjacent to this icons show one row containing specs of this phone (the idea is to show that all data that we encounter can be viewed as vectors) - the black boxes will be replaced by icons
- Show an icon of a customer. Now adjacent to this icon show one row containing details of this customer
- Show an icon of an MNIST digit and then show a vector
in each of the above case mention the dimension of the vector as R^?
Matrices
What are they ?
(c) One Fourth Labs

column vector
row vector
Matrices
How do you add two matrices ?
(c) One Fourth Labs

Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

- What happens when a matrix hits a vector?
- The vector gets transformed into a new vector (it strays from its path).
- The vector may also get scaled (elongated or shortened) in the process.
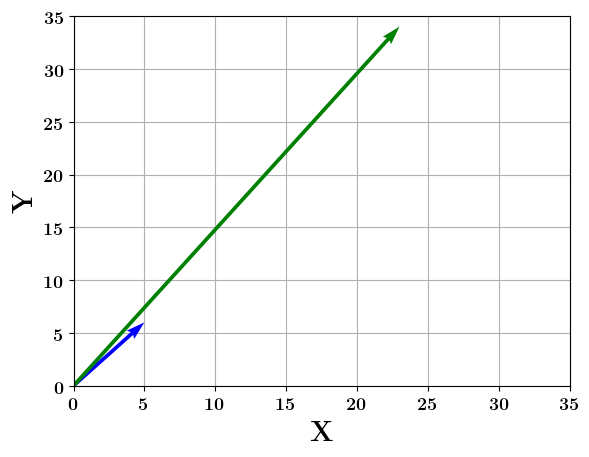
Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs



Similarly, in a 3D space, when a vector is hit by a matrix, it gets transformed into a new vector.
Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

?
illegal operation
Matrices
How do you multiply a matrix with a vector ?
(c) One Fourth Labs

legal operation
Conclusion : Number of columns in the matrix should be the same as the number of rows in the vector.
Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Number of columns in the matrix is not equal to the number of rows in the vector.
Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Number of columns in the matrix is equal to the number of rows in the vector.
Matrices
How do you multiply two matrices ?
(c) One Fourth Labs

Conclusion : Any m x n matrix can be multiplied with a n x k matrix to get a m x k output.
Matrices
Is there an alternate way of multiplying matrices ?
(c) One Fourth Labs

Matrices
Is there an alternate way of multiplying matrices ?
(c) One Fourth Labs

Matrices
What is the common operation that you will see in this course ?
(c) One Fourth Labs


| Weight (g) | Screen Size(in.) | Dual SIM | Radio | Battery (mAh) | Price (INR) | . . . | Internal Memory (GB) |
|---|

| 151 | 5.8 | 1 | 1 | 3060 | 15000 | . . . | 64 |
| 180 | 6.18 | 1 | 0 | 3500 | 32000 | . . . | 64 |
| 160 | 5.84 | 0 | 0 | 3060 | 25000 | . . . | 64 |
| 205 | 6.2 | 0 | 1 | 5000 | 18000 | . . . | 64 |
| 162 | 5.9 | 0 | 1 | 3000 | 14000 | . . . | 64 |
| 182 | 6.26 | 1 | 1 | 4000 | 12000 | . . . | 64 |
| 138 | 4.7 | 0 | 0 | 1960 | 35000 | . . . | 64 |
| 185 | 6.41 | 1 | 0 | 3700 | 42000 | . . . | 64 |
| 170 | 5.5 | 0 | 0 | 3260 | 44000 | . . . | 64 |
Why do we care about them ?
(c) One Fourth Labs
Matrices








Why do we care about them ?
(c) One Fourth Labs
Matrices








| F1 | F2 | F3 | F4 | F5 | F6 | ... | Fn |
|---|

Why do we care about them ?
(c) One Fourth Labs
Matrices
| F1 | F2 | F3 | F4 | F5 | F6 | ... | Fn |
|---|