An toàn bảo mật thông tin
Đề tài : Tìm hiểu Hệ mật mã RSA
Thành viên:
- Nguyễn Tuấn Kiên
- Đỗ Văn Khanh
- Phùng Thế Hoàng
Outline
- Giới thiệu chung
- Mô tả hoạt động
- Điểm yếu
- Độ an toàn mã hóa
- Hiệu năng
- Ứng dụng RSA vào chữ ký điện tử
Hệ mật mã đối xứng không thỏa mãn được 2 mục tiêu an toàn:
- Xác thực
- Alice và Bob trao đổi thông tin bí mật
- Alice cần phải biết thông tin chắc chắn đến từ
Bob, và ngược lại
- Chống phủ nhận
- Alice và Bob trao đổi thông tin bí mật
- Nếu Alice đã gửi thông tin nào đó cho Bob thì
Alice không thể chối bỏ thông tin đó là của mình
1. Giới thiệu chung
Tại sao lại cần Hệ mật mã công khai?
1. Giới thiệu chung
Tại sao lại cần Hệ mật mã công khai?
Quản lý khóa đối xứng là một vấn đề nan giải
-
Trong các hệ khóa đối xứng, mỗi cặp
người dùng phải có khóa riêng
-
N người dùng cần N * (N-1)/2 khóa
-
Việc quản lý khóa trở nên phức tạp khi
số lượng người dùng tăng
Hệ mật mã khóa công khai (PKC) ra đời
1. Giới thiệu chung
Hệ mật mã công khai
- Mỗi người dùng có 1 khóa riêng và 1 khóa công khai
- Khóa riêng bí mật
- Khóa công khai có thể chia sẻ
- Quản lý khóa
- N người dùng cần N khóa công khai được xác thực
- Hạ tầng quản lý khóa công khai PKI
1. Giới thiệu chung
Hệ mật mã công khai
Các thuật toán mã khóa công khai phổ biến:
- Merkle - Hellman Trapdoor Knapsack(Cửa bẫy dựa trên bài toán đóng thùng)
- RSA
- Paillier
- ElGamal
- ...
Thuật toán RSA - Lịch sử
Năm 1977,hệ mật mã khóa công khai RSA được Ron Rivest, Adi Shamir và Len Adleman(R.S.A) mô tả lần đầu tiên.

Trước đó, vào năm 1973, Clifford Cocks - một nhà toán học người Anh đã mô tả một thuật toán tương tự.
Nhưng tại thời điểm đó thì thuật toán này không khả thi và chưa bao giờ được thực nghiệm

1. Giới thiệu chung
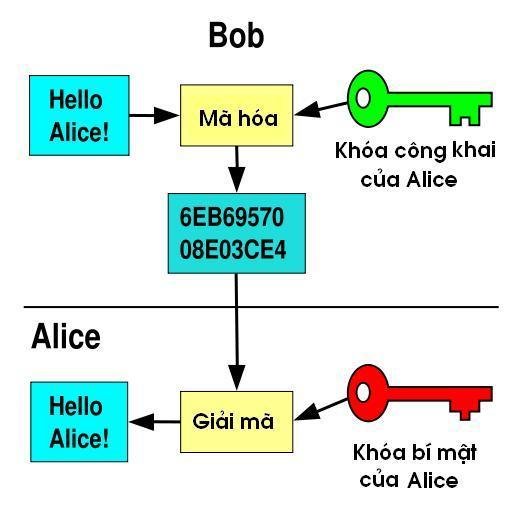
Thuật toán RSA có hai Khóa:
- Khóa công khai (Public key): được công bố rộng rãi cho mọi người và được dùng để mã hóa
- Khóa bí mật (Private key): Những thông tin được mã hóa bằng khóa công khai chỉ có thể được giải mã bằng khóa bí mật tương ứng
2. Mô tả hoạt động
2. Mô tả hoạt động
Chọn 2 số nguyên tố p,q
Tính n = p * q
Tính Φ(n) = (p-1)* (q-1)
Chọn e, 0 < e < Φ(n),sao cho UCLN(e,Φ(n)) = 1
Tìm d sao cho e * d = 1 mod Φ(n)
c = m^e mod n
m = c ^d mod n
Bản rõ m
Bản mã c
Bản rõ m
LÝ THUYẾT
VÍ DỤ
2. Mô tả hoạt động
Bước 1: B (người nhận) tạo hai số nguyên tố lớn ngẫu nhiên p và q
Bước 1: Chọn số p = 11 và q = 23
(hai số này là 2 số nguyên tố)
Bước 2: Tính n=p*q và Φ(n) = (p-1)* (q-1)
Bước 2: n = 11 * 23 = 253
Φ(n) = 10 * 22 = 220
Bước 3: chọn một số ngẫu nhiên e
(0< e < Φ(n)) sao choƯCLN(e,Φ(n))=1
Bước 3: chọn e = 3 vì ƯCLN(3, 220) = 1
Bước 4: tính d = e^-1 (mod m) (dùng thuật toán Euclide mở rộng)
Bước 4: d = 147
Bước 5: Khóa công khai: (e,n)
Khóa bí mật : (d,p,q)
Bước 5: Khóa công khai: (3,253)
Khóa bí mật: (147,11,23)
2.2. Tạo khóa
2. Mô tả hoạt động
2.2. Mã hóa và giải mã
LÝ THUYẾT
VÍ DỤ
Bước 1:A nhận khóa công khai của B
Bước 1:A nhận khóa công khai của b : (e,n) = (3,253)
Bước 2: A biểu diễn thông tin cần gửi thành số m (0<=m<=(n-1))
Bước 2: Thông tin cần gửi
m = 165
Bước 3: Tính
c = m^e mod n
Bước 3: Tính
c = 165^3 mod 253 = 110
Bước 4: Gửi c cho B
Bước 4: Gửi c = 110
Bước 5: Giải mã
m = c^d mod n
Bước 5: Giải mã
m = 110^147 mod 253 = 165
2. Mô tả hoạt động
2.3. Một vài định lý
ĐỊNH LÝ RSA
Nếu:
- (e,n) là khóa công khai
- (d,p,q) là khóa bí mật
- 0 <= m < n
thì:
(m^e)^d mod n = m
2.3. Một vài định lý
2. Mô tả hoạt động
ĐỊNH LÝ EULER & FERMAT
Nếu:
- ef(n) là số “số nguyên dương nhỏ hơn n và nguyên tố cùng nhau với n”
- x và n là hai số nguyên tố cùng nhau
thì:
x^ef(n) = 1 mod n
3. Điểm yếu của RSA
Không phải lúc nào thông tin cũng được che giấu tốt,tức là mọi khóa đều tốt và đều làm thay đổi bản rõ hoàn toàn.
Ví dụ:
Có: Bản rõ m = 8
Chọn p = 5,q = 7
Tính ra n = 35,Φ(n) = 24
Chọn e = 5 thỏa mãn UCLN(e,Φ(n)) = 1
Mã hóa
c = m^e mod n
Bản mã: c = 8
4. Độ an toàn của RSA
- Độ an toàn của hệ thống RSA dựa trên 2 vấn đề: bài toán phân tích ra thừa số nguyên tố các số nguyên lớn và bài toán RSA.
- Vì vậy muốn xây dựng hệ RSA an toàn thì n=p*q phải là một số đủ lớn, để không có khả năng phân tích nó về mặt tính toán. Để đảm bảo an toàn nên chọn các sốnguyên tố p và q từ 100 chữ số trở lên(512bit trở lên). p và q phải xấp xỉ nhau.
- Lựa chọn e: e phải nhỏ nhất có thể,nhưng không quá nhỏ để tránh bị tấn công theo dạng “low exponent”.
- Lựa chọn d: d không nhỏ quá (d < n/4) để tránh tấn công dạng “low decryption”
- Dưới đây là bảng thời gian phân tích mã RSA
4. Độ an toàn của RSA
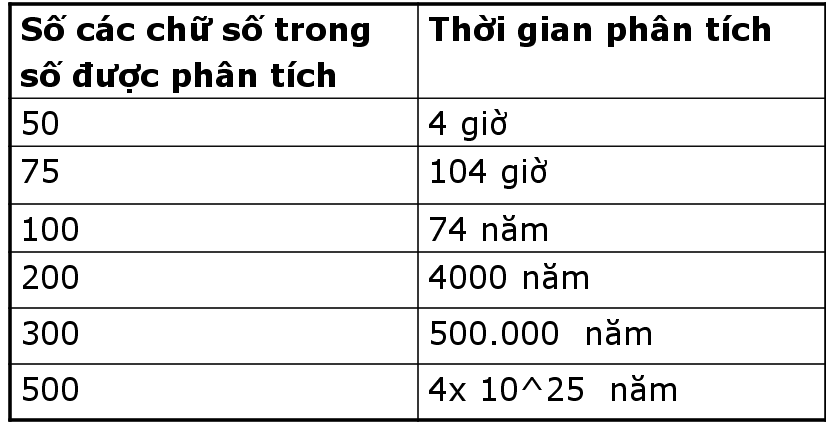
4. Độ an toàn của RSA
- Cách thức phân phối khóa công khai là một trong những yếu tố quyết định đối với độ an toàn của RSA.
-
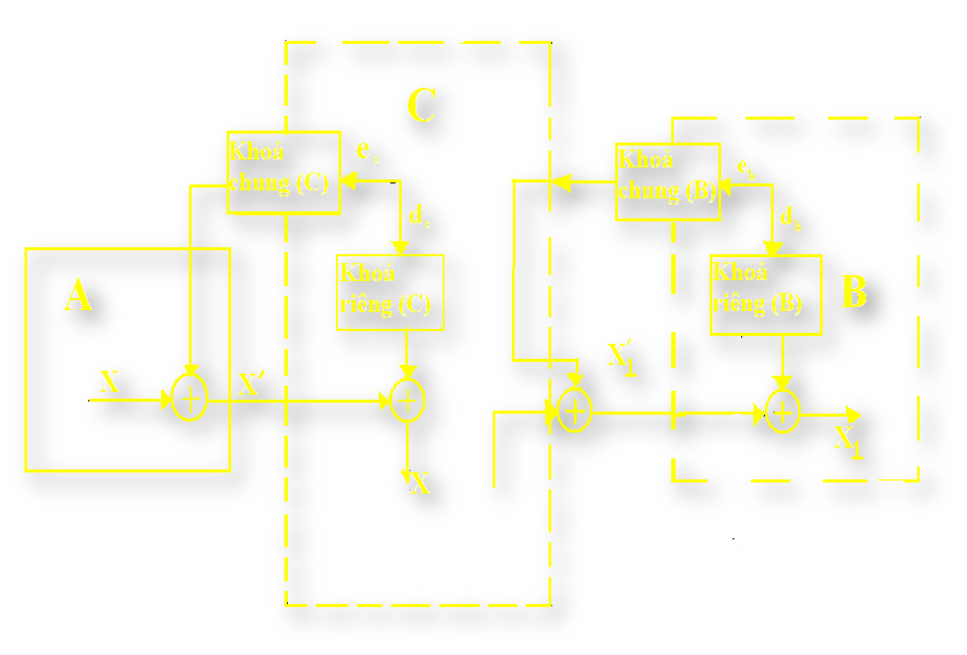
Vấn đề này nảy sinh ra 1 lỗ hổng gọi là Man-in-the-middle attack
- Khi A và B trao đổi thông tin thì C có thể gửi cho A một khóa bất kì để A tin rằng đó là khó công khai của B gửi
- Sau đó C sẽ giải mã và đánh cắp được thông tin.Đồng thời mã hóa lại thông tin theo khóa công khai của B và gửi lại cho B.
- Về nguyên tắc,cả A và B đều không phát hiện được sự can thiệp của C
4. Độ an toàn của RSA
5. Hiệu năng
So sánh RSA và DES:
Tốc độ mã hóa:
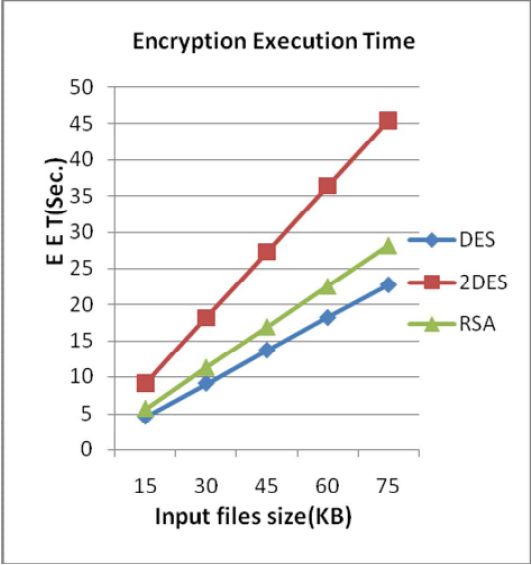

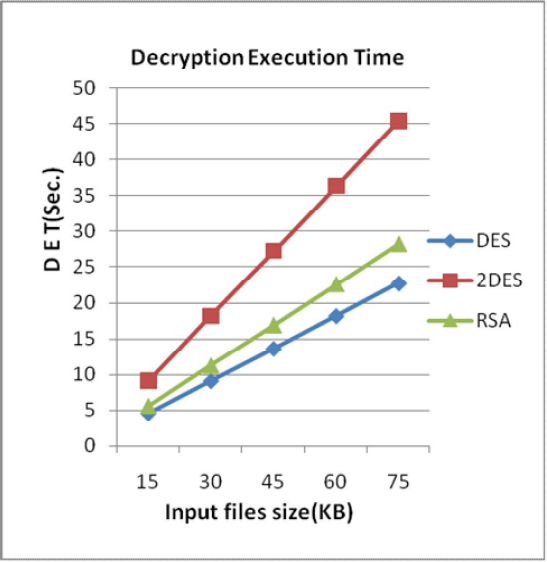
5. Hiệu năng
So sánh RSA và DES:
Tốc độ giải mã


6. Ứng dụng RSA vào chữ ký điện tử
Ứng dụng cơ bản của RSA:
- Bảo mật trong truyền tin
- Chứng thực
- Kết hợp tính mật và tin cậy
Trong đó,tạo chữ ký điện tử là ứng dụng lớn nhất của RSA.
6. Ứng dụng RSA vào chữ ký điện tử
- Thông tin truyền đi trên mạng cũng cần thiết phải được xác nhận người gửi.
- Các văn bản truyền trên mạng (dưới dạng số hoá) cần phải có chữ ký của người gửi để xác nhận trách nhiệm của người gửi.
- Chữ ký dùng ở đây là một dãy bit và được gọi là″chữ ký điện tử″.
- Mỗi người cần 1 cặp khóa gồm khóa công khai & khóa bí mật.
- Khóa bí mật dùng để tạo chữ ký số (CKS)
- Khóa công khai dùng để thẩm định CKS-> xác thực
6. Ứng dụng RSA vào chữ ký điện tử
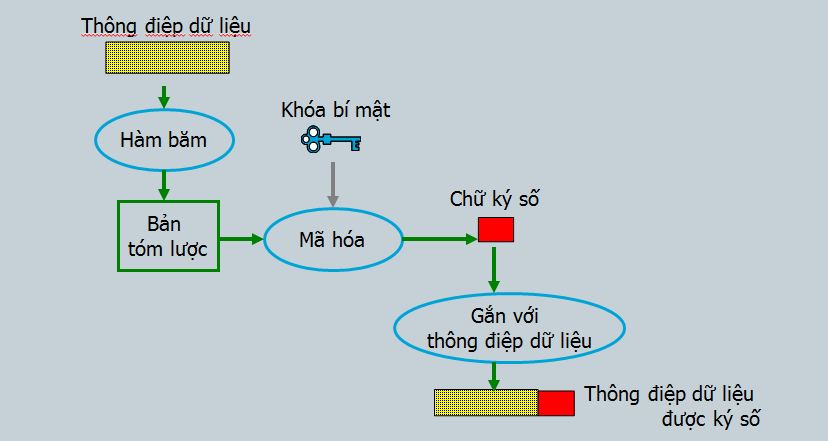
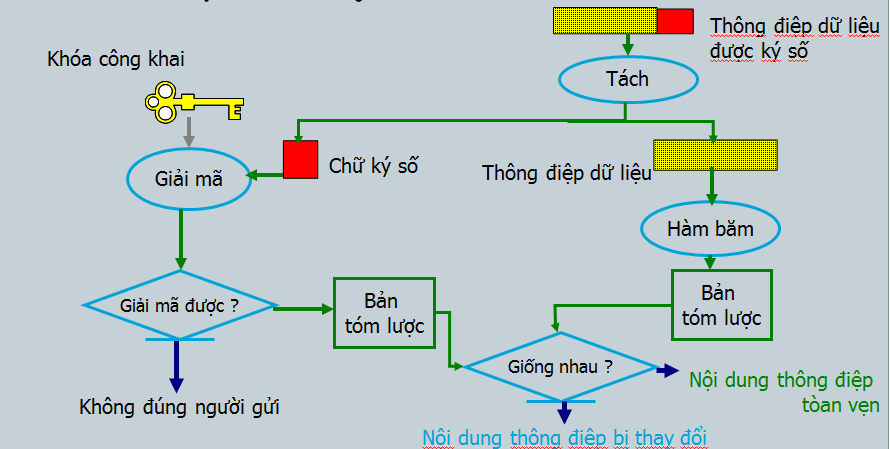
Tạo chữ ký số
Thẩm định chữ ký
Xin cám ơn mọi người đã lắng nghe