2.4 The progress of  DL over the past one decade

Better optimization, Better activation functions, Better weight initialization, Better regularizer, Better compute, More data

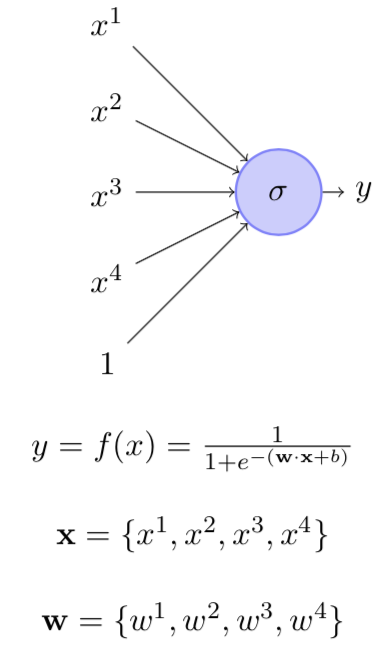
The DL story

 

A time line of where we are

-UAT

-Backpropagation

1989-1991

2006

- Revival by Hinton et. al. (Unsupervised Pre-Training)

2019

\overbrace{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}

- Better Learning Algos

- Better Initialization

- Better Activations

- Better Regularization

\frac{\partial L}{\partial w_{131}}= \frac{\partial L}{\partial \hat{y}_{2}}.\frac{\partial \hat{y}_{2}}{\partial a_{22}}.\frac{\partial a_{22}}{\partial h_{13}}.\frac{\partial h_{13}}{\partial a_{13}}.\frac{\partial a_{13}}{\partial w_{131}}
\underbrace{\quad\quad\quad\quad\quad\quad\quad}

- More data

- More compute

- More democratization

Better Learning algorithms

 

What are we going to see in this chapter ?

 

How do you use the gradients?

or

Can you come up with a better update rule ?

w = w - \eta \frac{\partial \mathscr{L}(w)}{\partial w}

Gradient Descent Update Rule

How do you compute the gradients ?

or

What data should you use for computing the gradients?

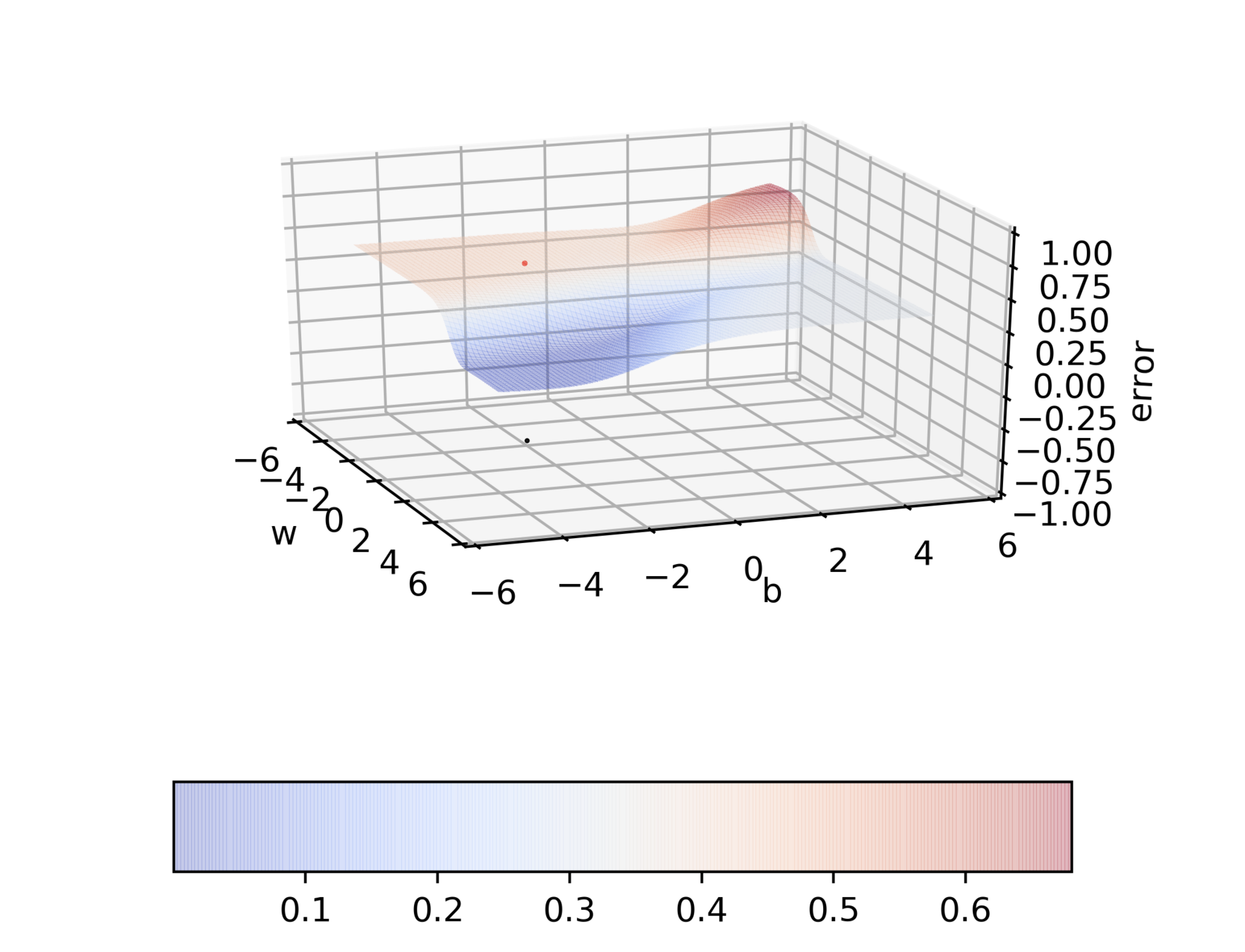
Some observations about GD

 

Do you observe something peculiar on different regions of the error surface?

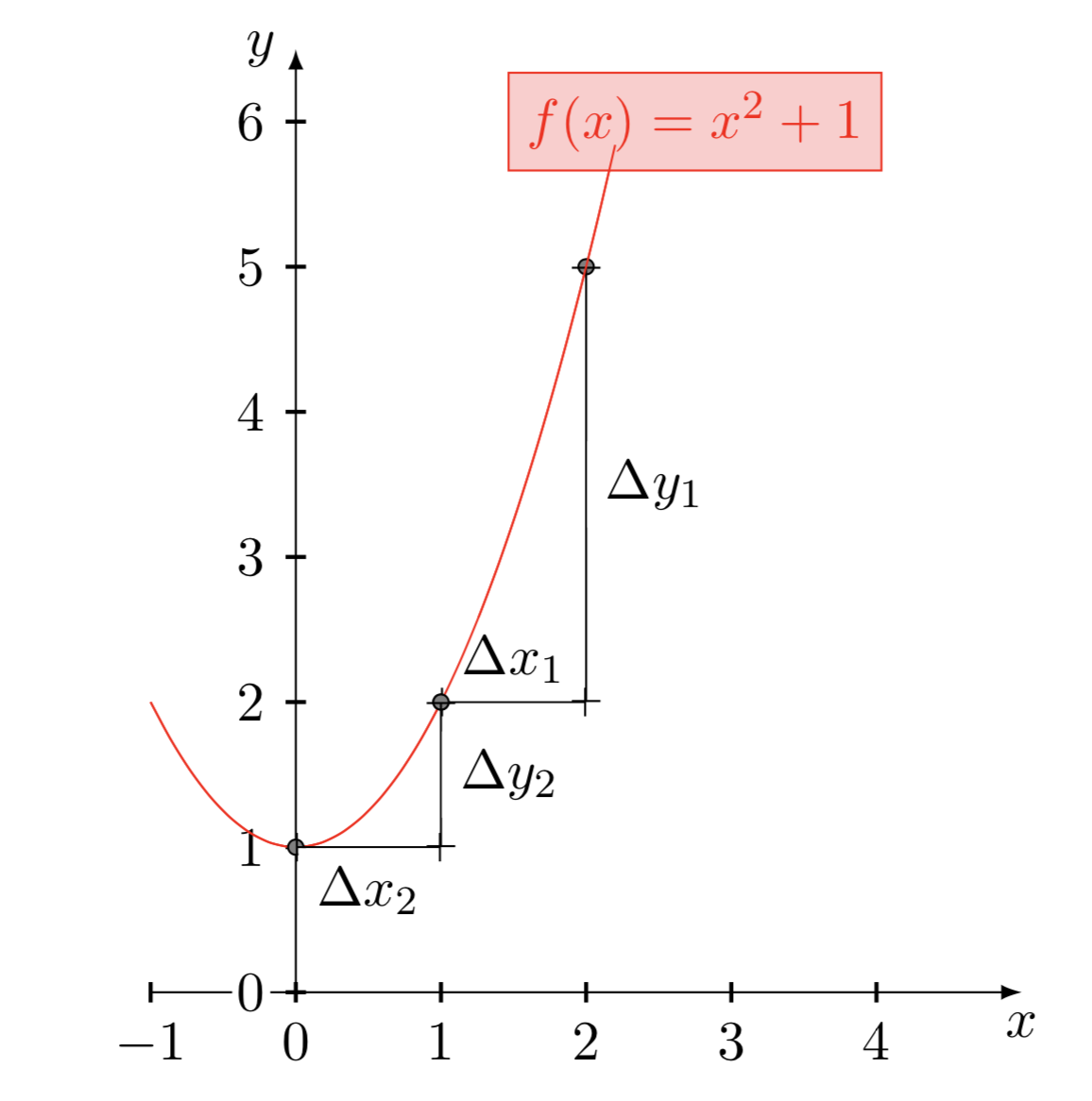
X = [0.5, 2.5]
Y = [0.2, 0.9]
def f(w, b, x):
   #sigmoid with parameters w, b
   return 1.0 / (1.0 + np.exp(-(w*x + b))
def error(w, b):
     err = 0.0
     for x, y in zip(X, Y): 
        fx = f(w, b, x)
        err += 0.5* (fx - y) ** 2
     return err
def grad_b(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx)

def do_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
        w = w - eta * dw
        b = b - eta * db 
             
def grad_w(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx) * x

Some observations about GD

 

Why is the behaviour different on different surfaces ?

w = w - \eta \frac{\partial \mathscr{L}(w)}{\partial w}

Gradient Descent Update Rule

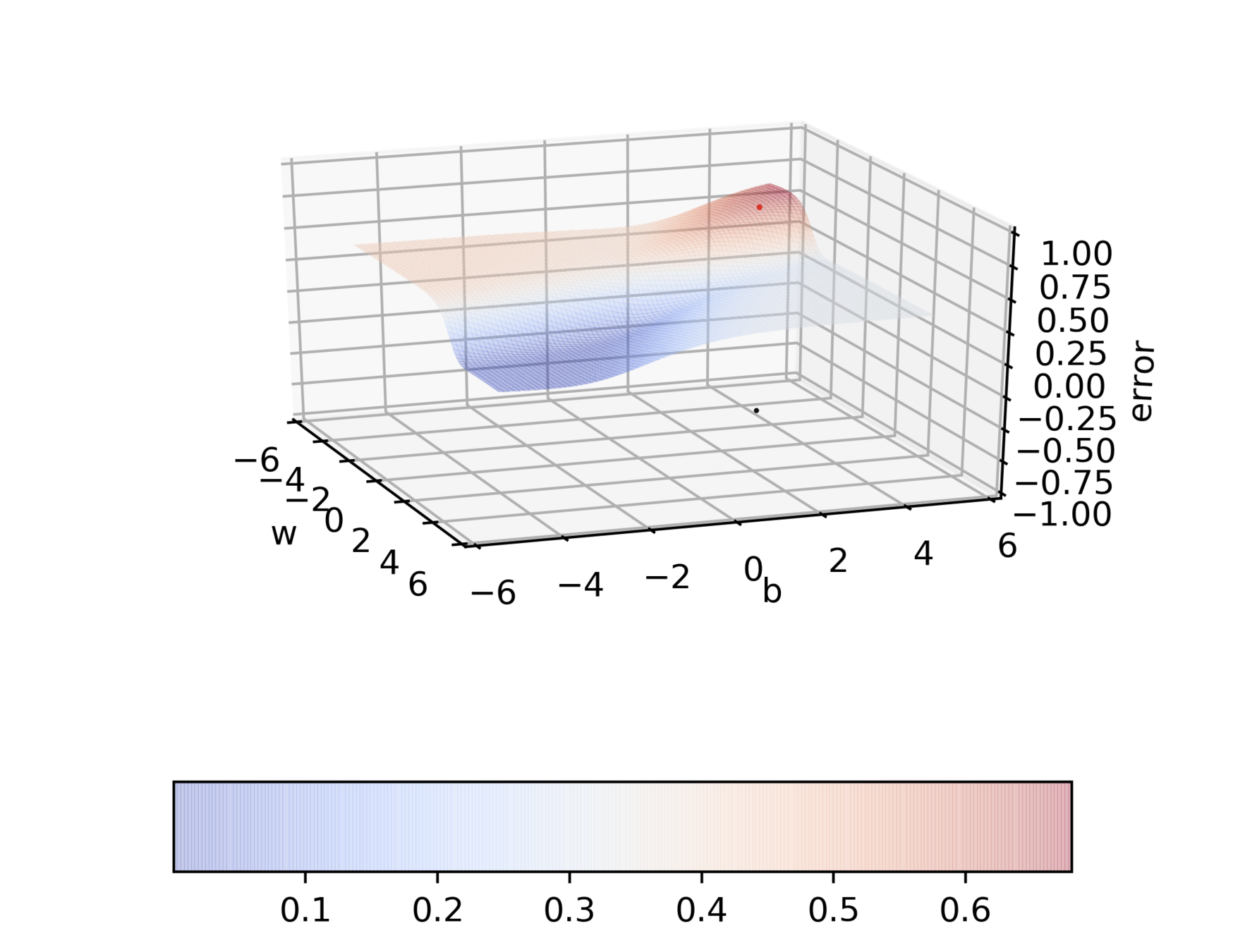
Some observations about GD

 

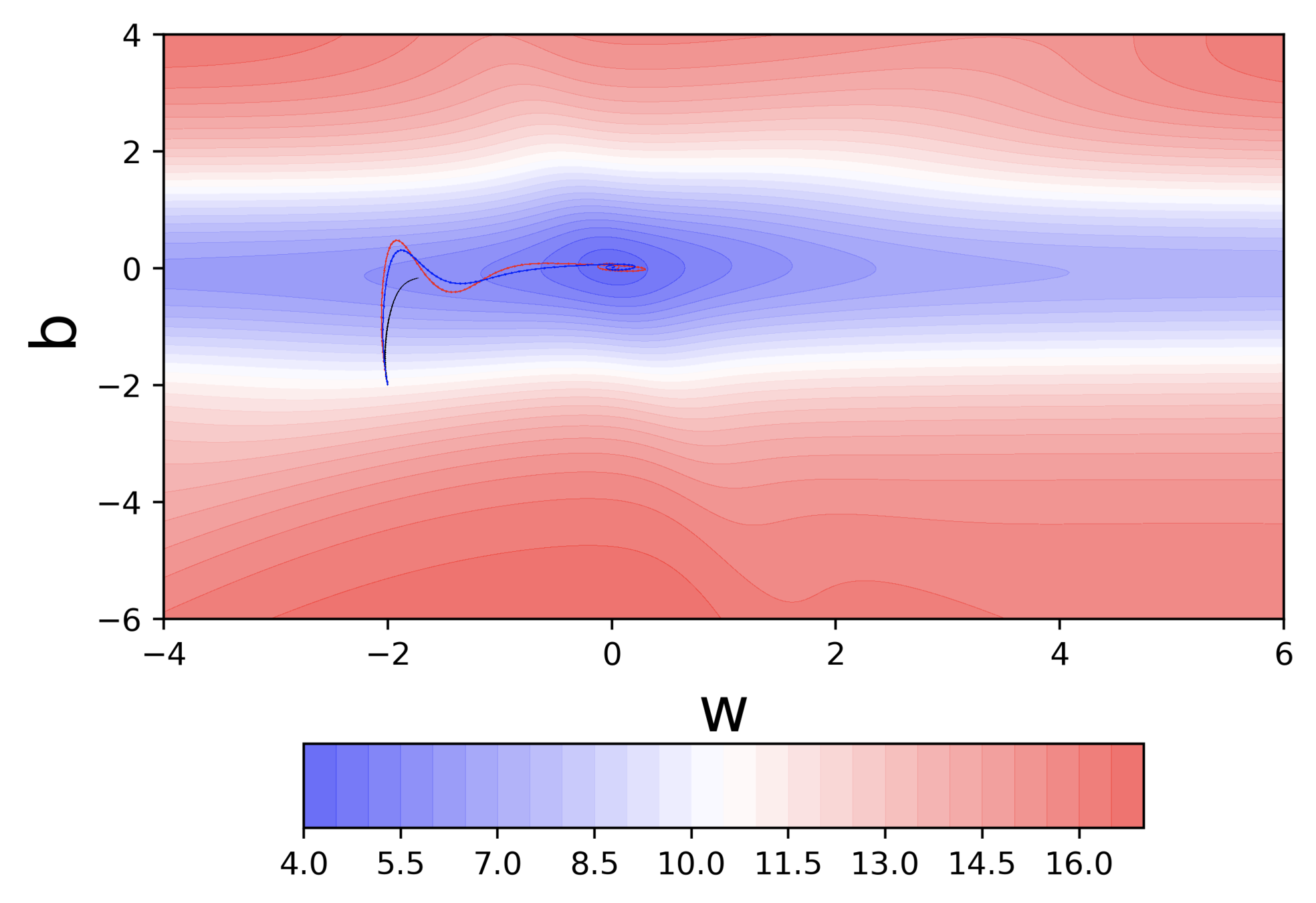
Do we observe the same behaviour if we start from a different initialization ?

Some observations about GD

 

Why does this behavior bother us ?

Initialise 

\(w, b \)

Iterate over data:

\(w_{t+1} = w_{t} - \eta \Delta w_{t} \)

till satisfied

\(b_{t+1} = b_{t} - \eta \Delta b_{t} \)

compute ~ \hat{y}
compute ~ \mathscr{L}(w, b)

randomly 

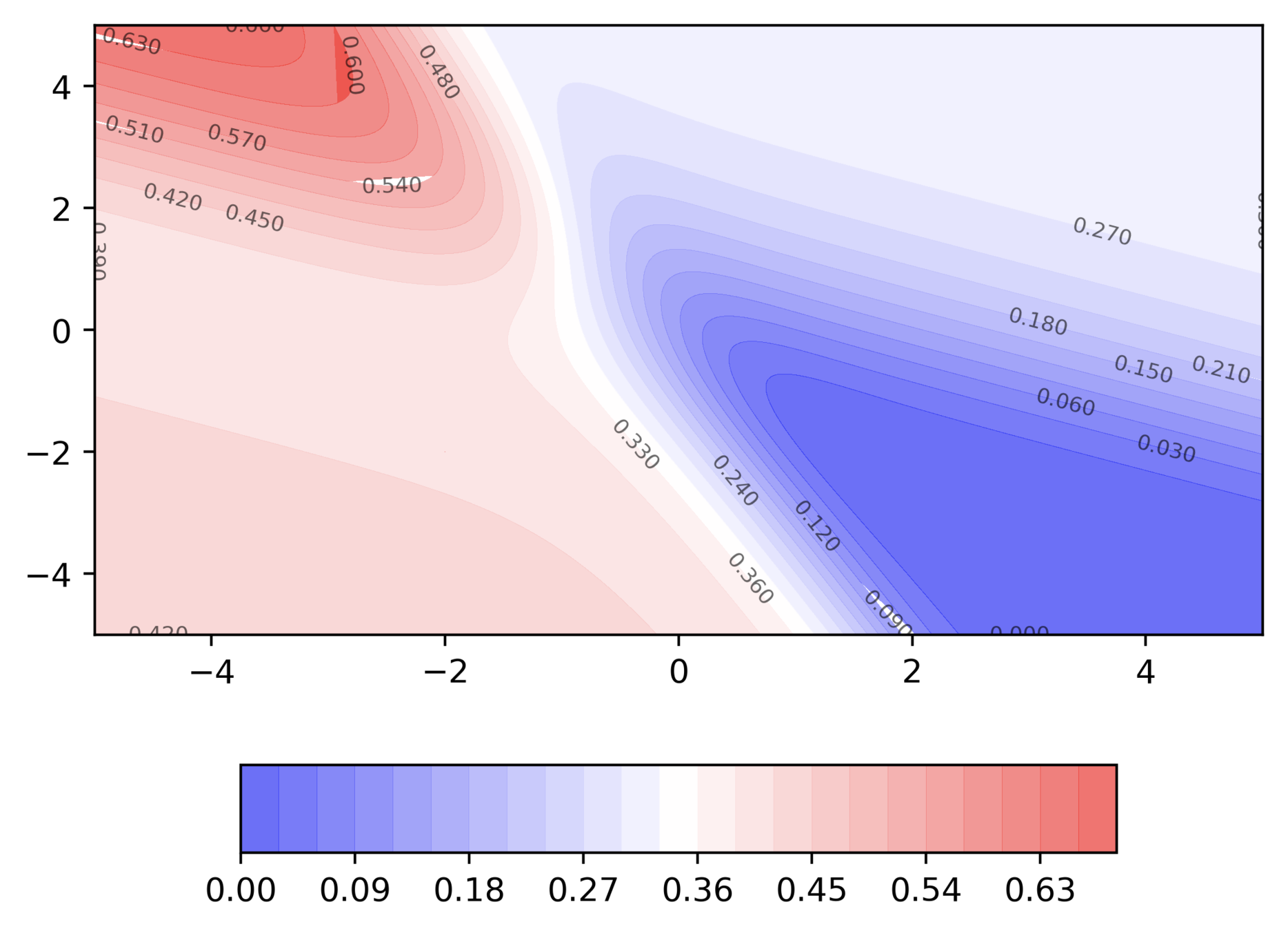
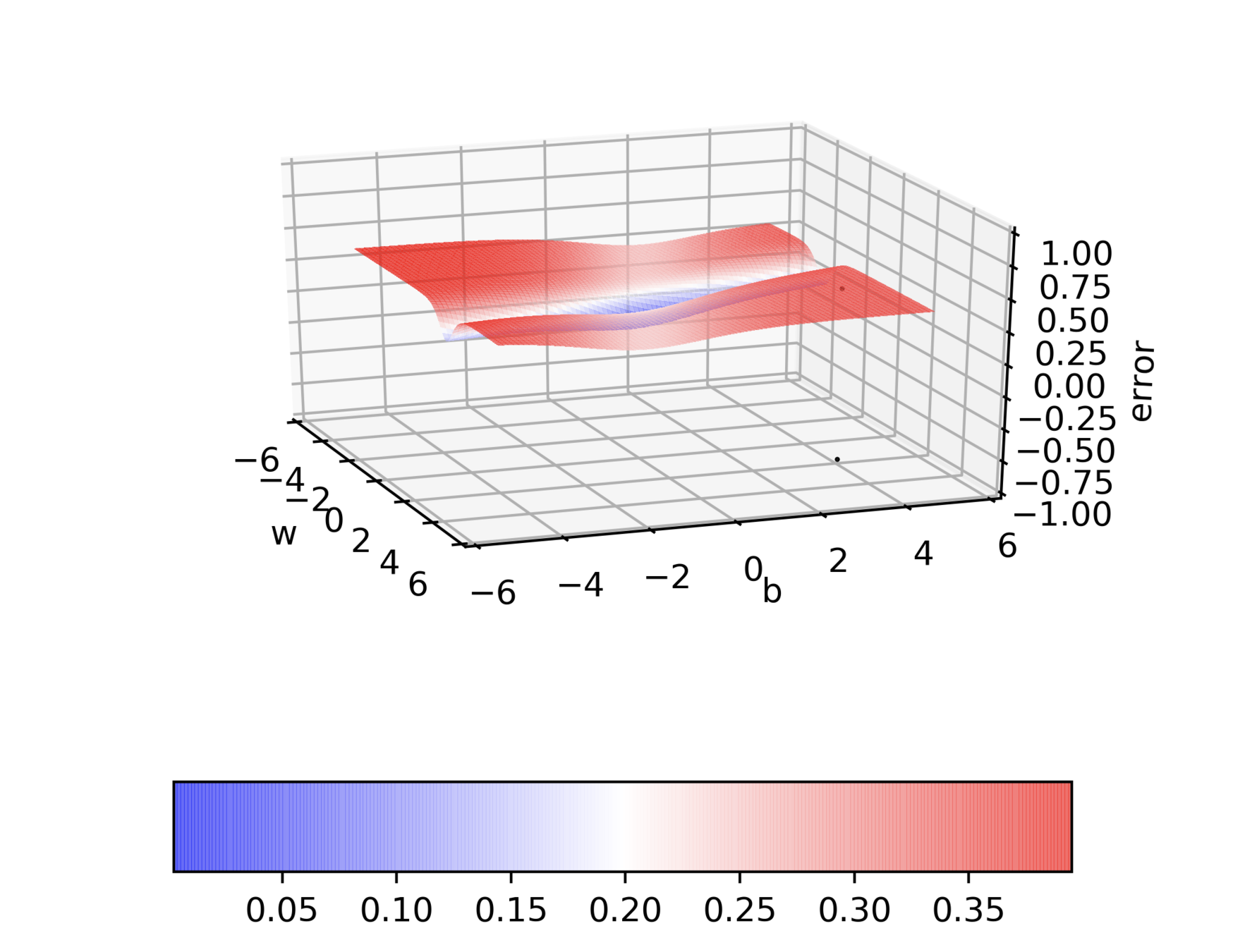
A detour into contour maps

 

Can we visualize things in 2D instead of 3D ?

  • A small distance between contours indicates a steep slope along that direction
  • A large distance between contours indicates a gentle slope along that direction

A detour into contour maps

 

Can we do a few exercises?

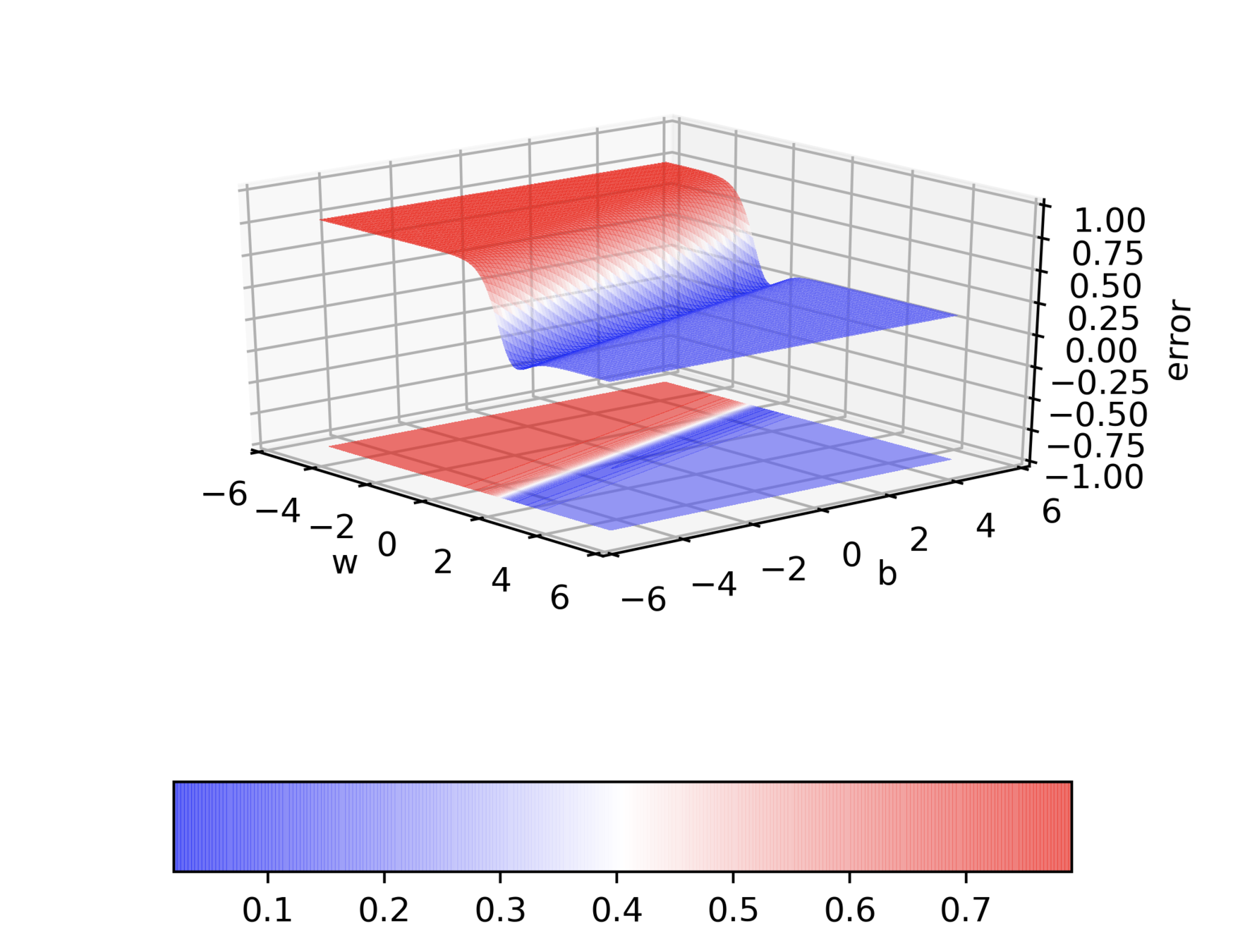
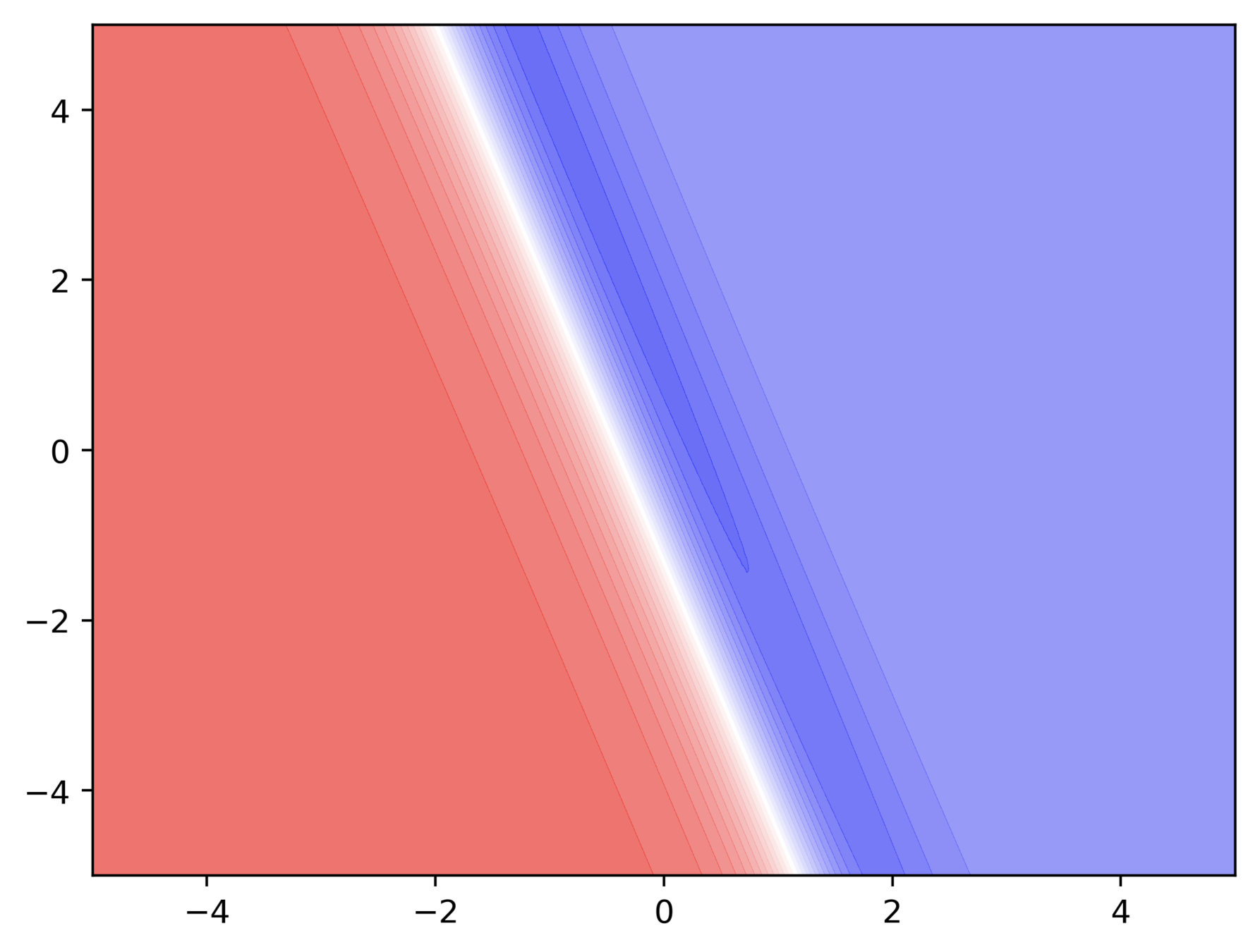
A detour into contour maps

 

Can we do a few exercises?

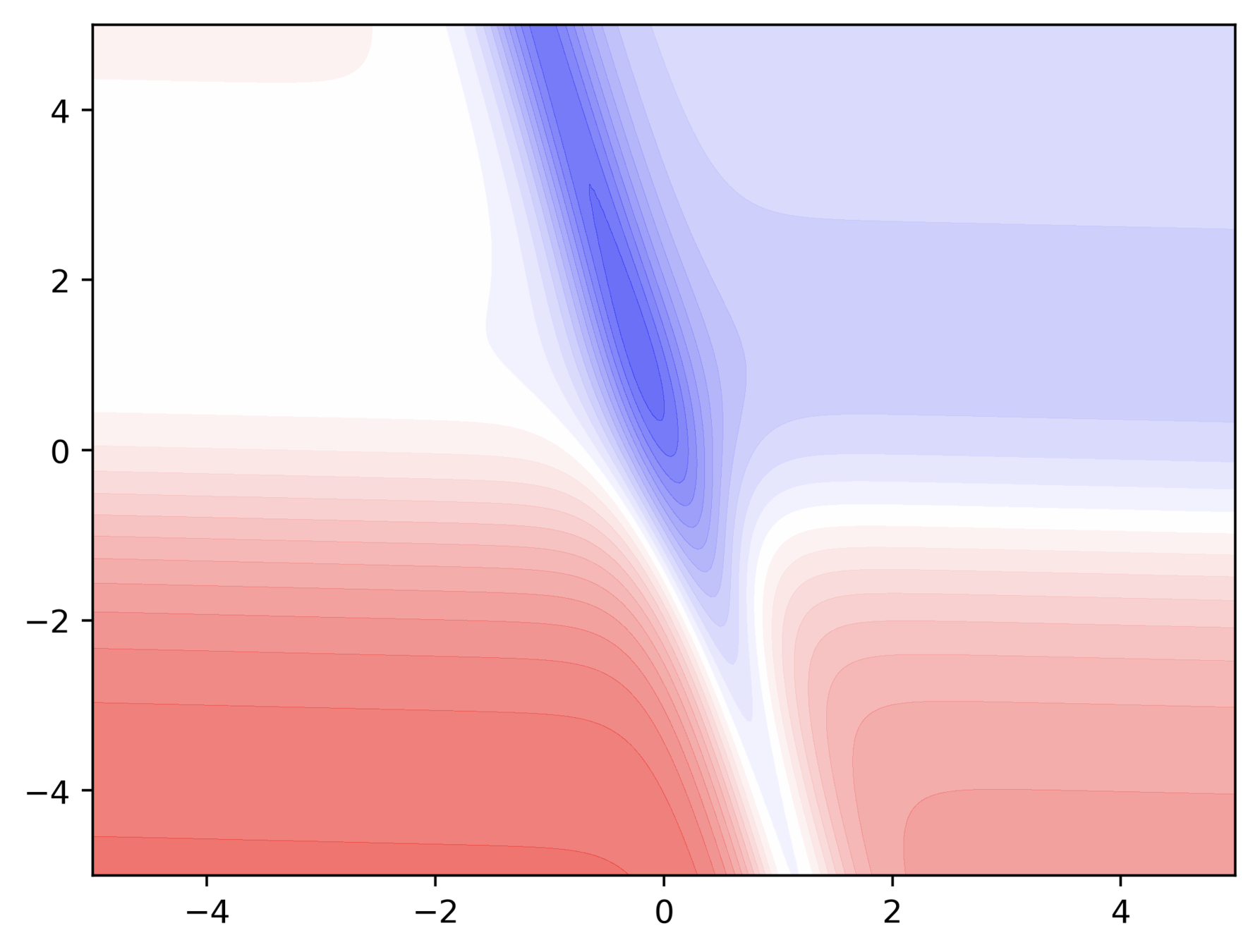
A detour into contour maps

 

Can we do a few exercises?

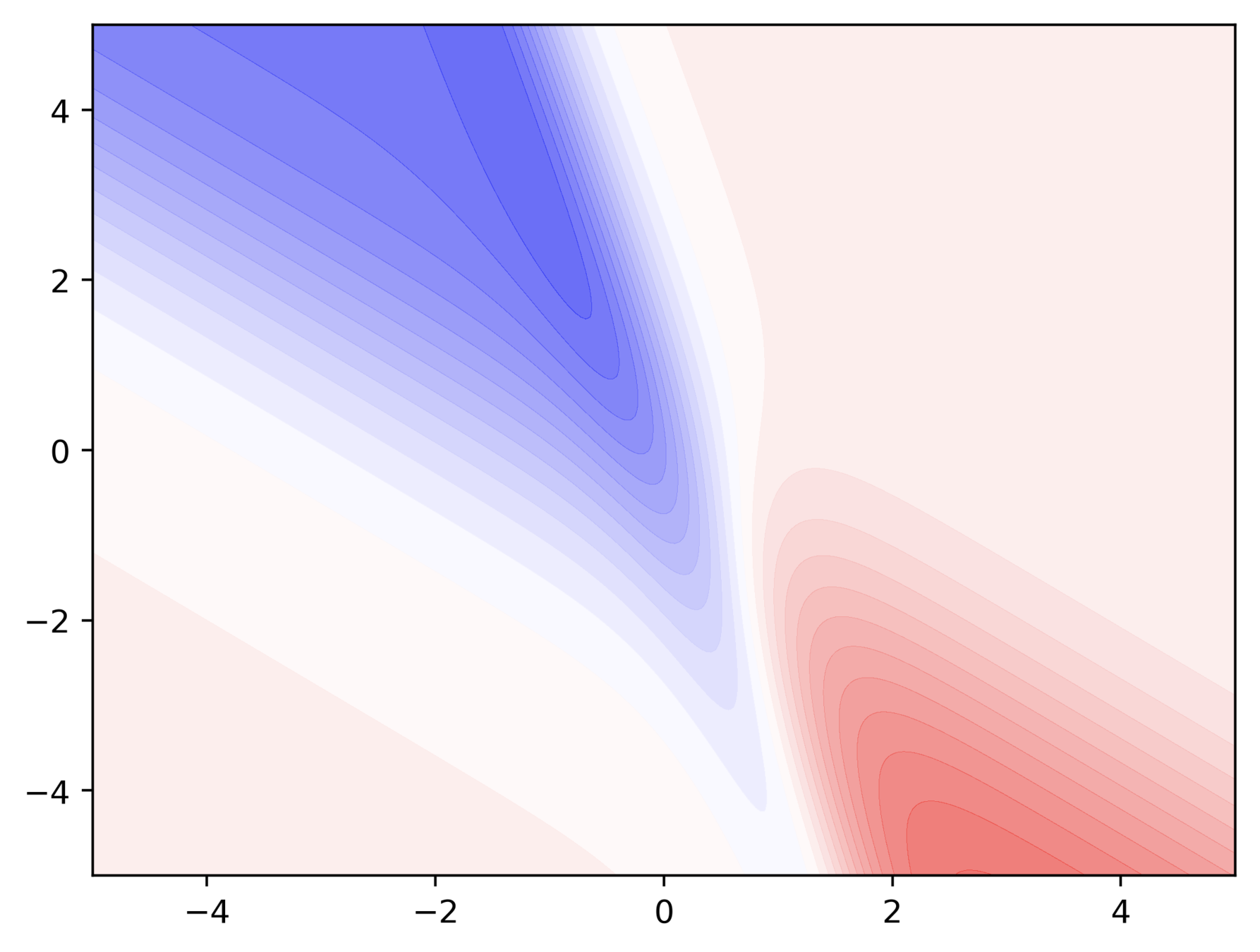
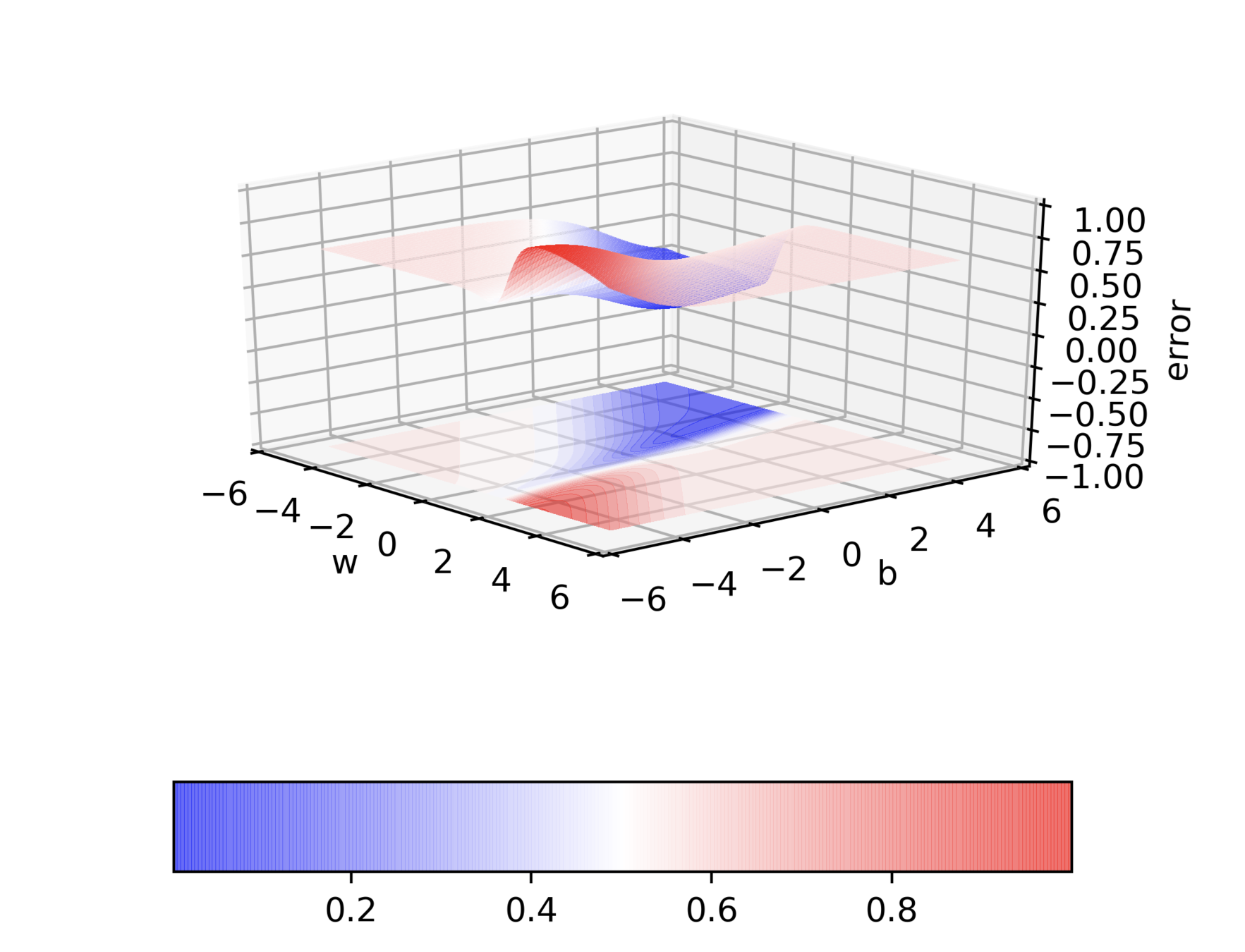
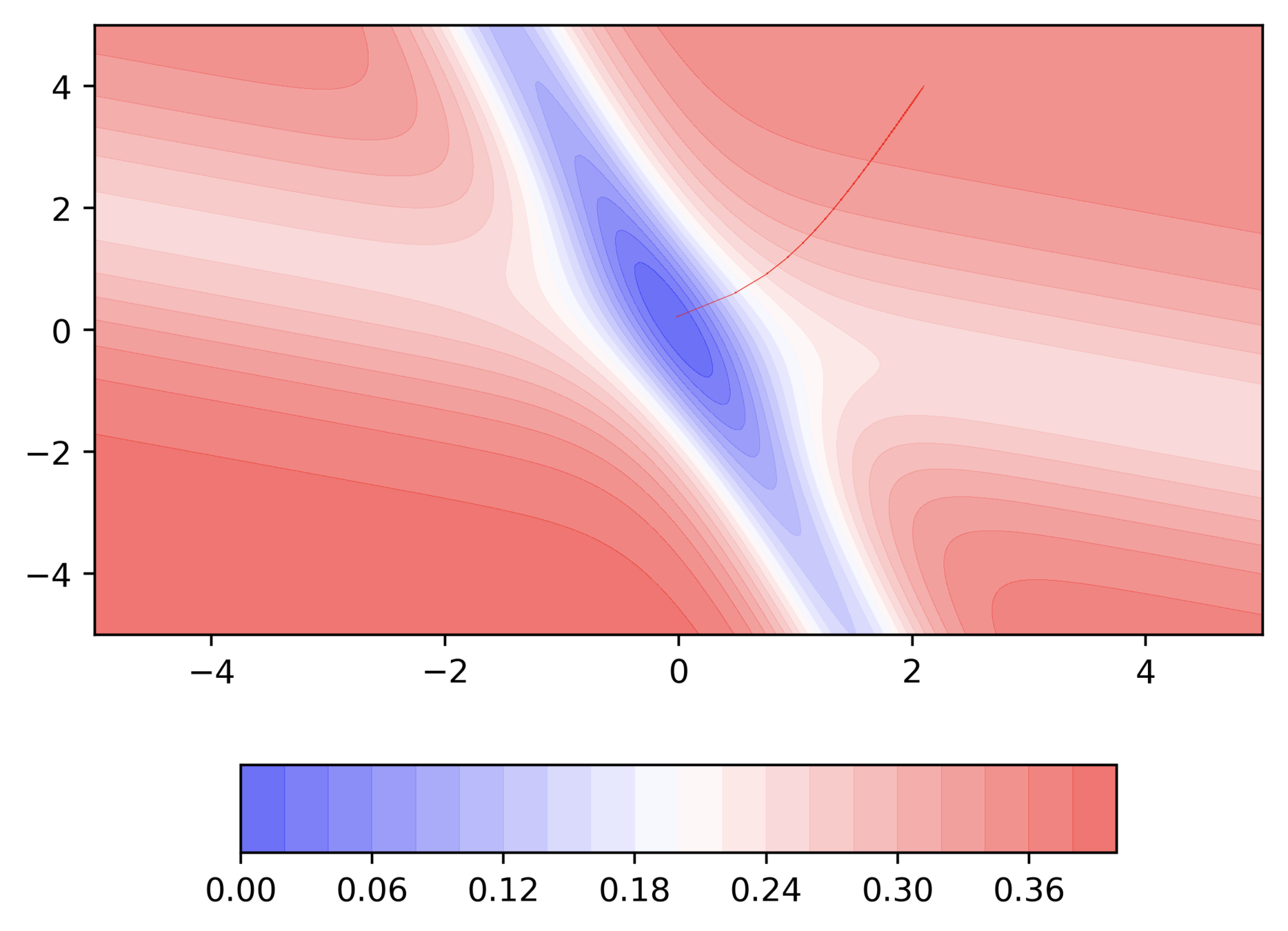
And we are back to GD

 

Can we visualize Gradient Descent on a 2d error surface ?

Momentum based GD

 

Why do we need a better algorithm ?

Issues

 

It takes a lot of time to navigate regions having gentle slope (because the gradient in these regions is very small)

Intuitive Solution

 

If I am repeatedly being asked to go in the sam direction then I should probably gain some confidence and start taking bigger steps in that direction

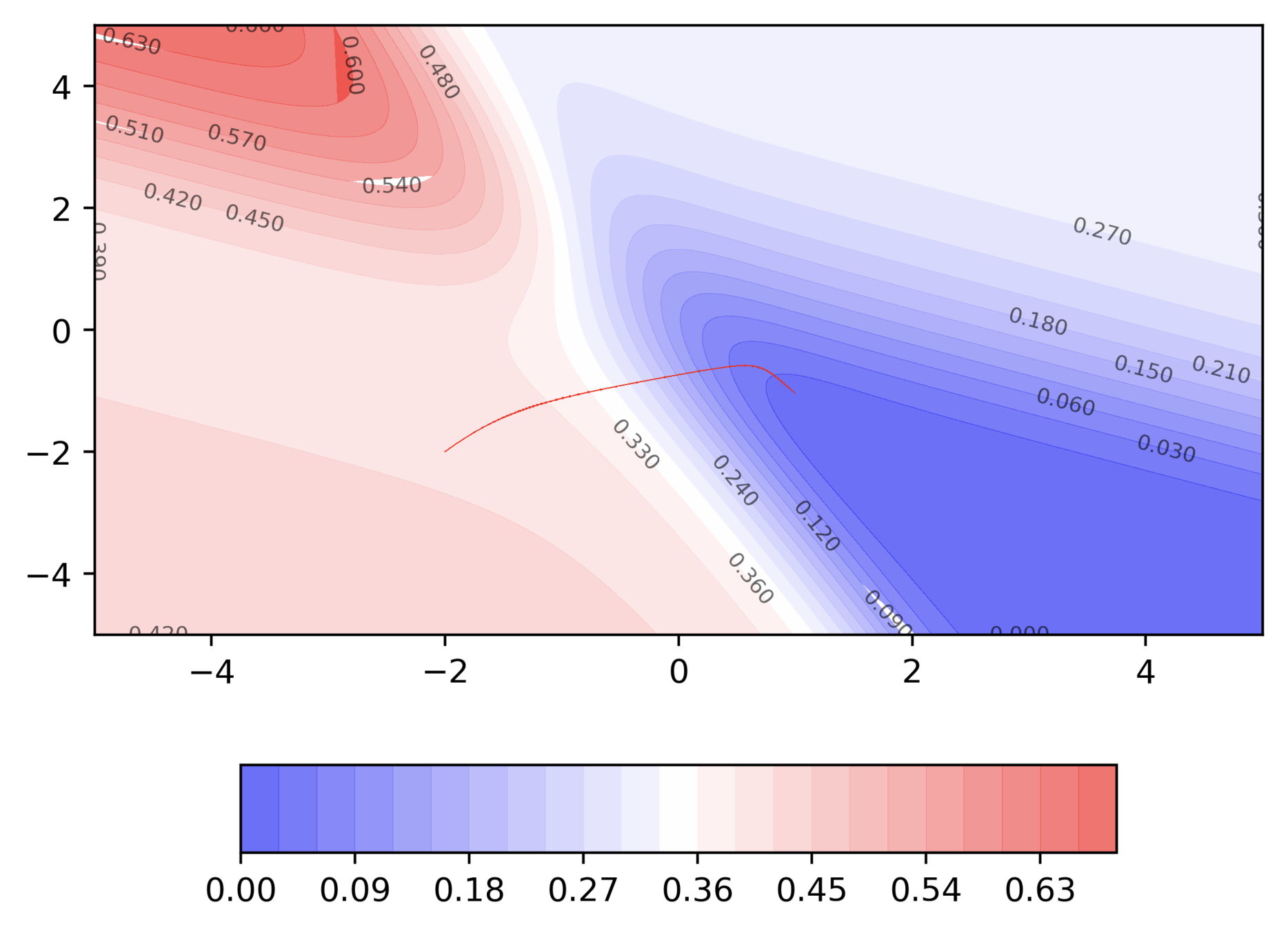
Momentum based GD

 

How do we convert this intuition into a set of mathematical equations

w_{t+1} = w_t - \eta \nabla w_t

Gradient Descent Update Rule

\begin{aligned} v_t &= \gamma * v_{t-1} + \eta \nabla w_{t} \\ w_{t+1} &= w_t - v_t \end{aligned}

Momentum based Gradient Descent Update Rule

Momentum based GD

 

Can we dissect the equations in more detail ?

\begin{aligned} v_{t} &= \gamma\cdot v_{t-1} + \eta \nabla w_{t} \\ w_{t+1} &= w_{t} - v_{t} \end{aligned}
\begin{aligned} v_{0} & = 0\\ v_{1} & = \gamma\cdot v_{0} + \eta \nabla w_{1} = \eta \nabla w_{1}\\ v_{2} & = \gamma\cdot v_{1} + \eta \nabla w_{2} = \gamma\cdot \eta \nabla w_{1} + \eta \nabla w_{2}\\ v_{3} & = \gamma\cdot v_{2} + \eta \nabla w_{3} = \gamma (\gamma \cdot \eta \nabla w_{1} + \eta \nabla w_{2}) + \eta \nabla w_{3}\\ & = \gamma\cdot v_{2} + \eta \nabla w_{3} = \gamma^2 \cdot \eta \nabla w_{1} + \gamma \cdot \eta \nabla w_{2} + \eta \nabla w_{3}\\ v_{4} & = \gamma\cdot v_{3} + \eta \nabla w_{4} = \gamma^3 \cdot \eta \nabla w_{1} + \gamma^2 \cdot \eta \nabla w_{2} + \gamma \cdot \eta \nabla w_{3} + \eta \nabla w_{4} \\ \vdots\\ v_{t} & = \gamma\cdot v_{t-1} + \eta \nabla w_{t} = \gamma^{t-1} \cdot \eta \nabla w_{1} + \gamma^{t-2} \cdot \eta \nabla w_{1} + ... + \eta \nabla w_{t}\\ \end{aligned}

Exponentially decaying weighted sum

Momentum based GD

 

Let' see the code for this

X = [0.5, 2.5]
Y = [0.2, 0.9]
def f(w, b, x):
   #sigmoid with parameters w, b
   return 1.0 / (1.0 + np.exp(-(w*x + b))
def error(w, b):
     err = 0.0
     for x, y in zip(X, Y): 
        fx = f(w, b, x)
        err += 0.5* (fx - y) ** 2
     return err
def grad_b(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx)

def do_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
        w = w - eta * dw
        b = b - eta * db 
             
def grad_w(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx) * x

def do_momentum_gradient_descent():
    w, b, eta, max_epochs = -2, -2, 1.0, 1000
    v_w, v_b = 0, 0
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
        v_w = gamma*v_w + eta * dw
        v_b = gamma*v_b + eta * dw

        w = w - v_w
        b = b - v_w
\begin{aligned} v_t &= \gamma * v_{t-1} + \eta \nabla w_t \\ w_{t+1} &= w_t - v_t \end{aligned}

Momentum based Gradient Descent Update Rule

Momentum based GD

 

Let's run this code

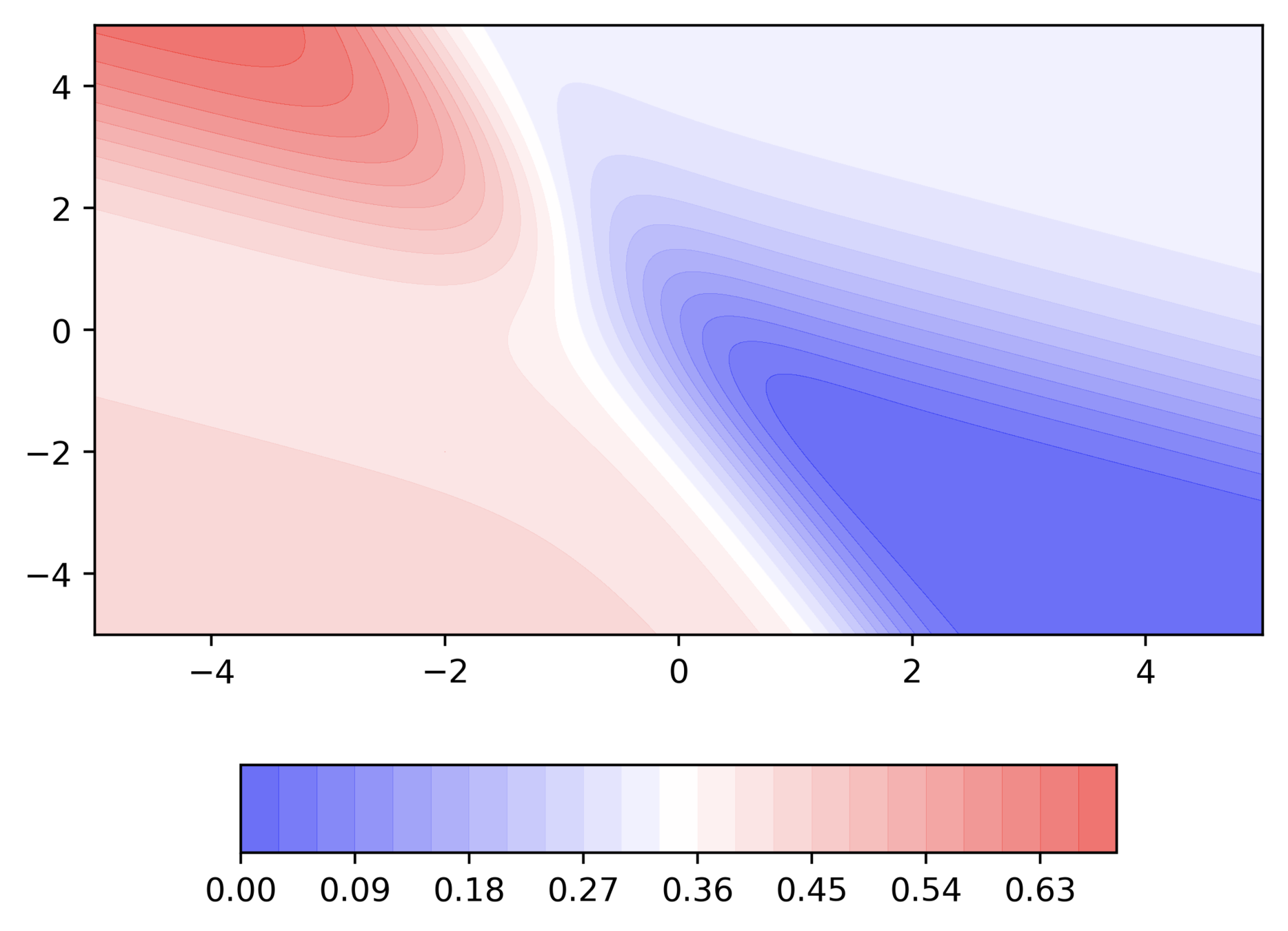
Momentum based GD

 

Let us make a few observations and ask some questions

Observations

 

Even in the regions having gentle slopes, momentum based gradient descent is able to take large steps because the momentum carries it along

Questions

 

- Is moving fast always good?

- Would there be a situation where momentum would cause us to run pass our goal?

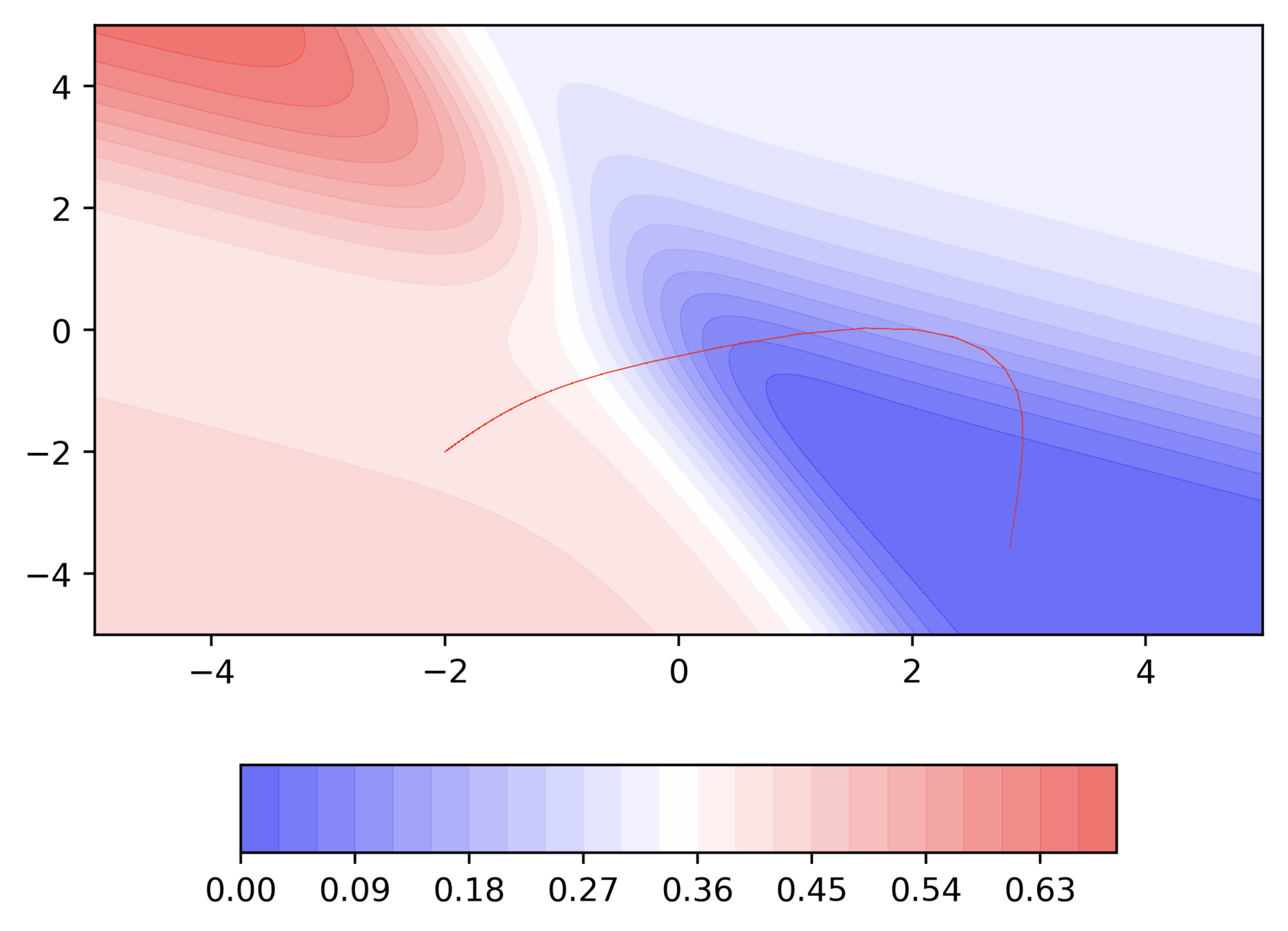
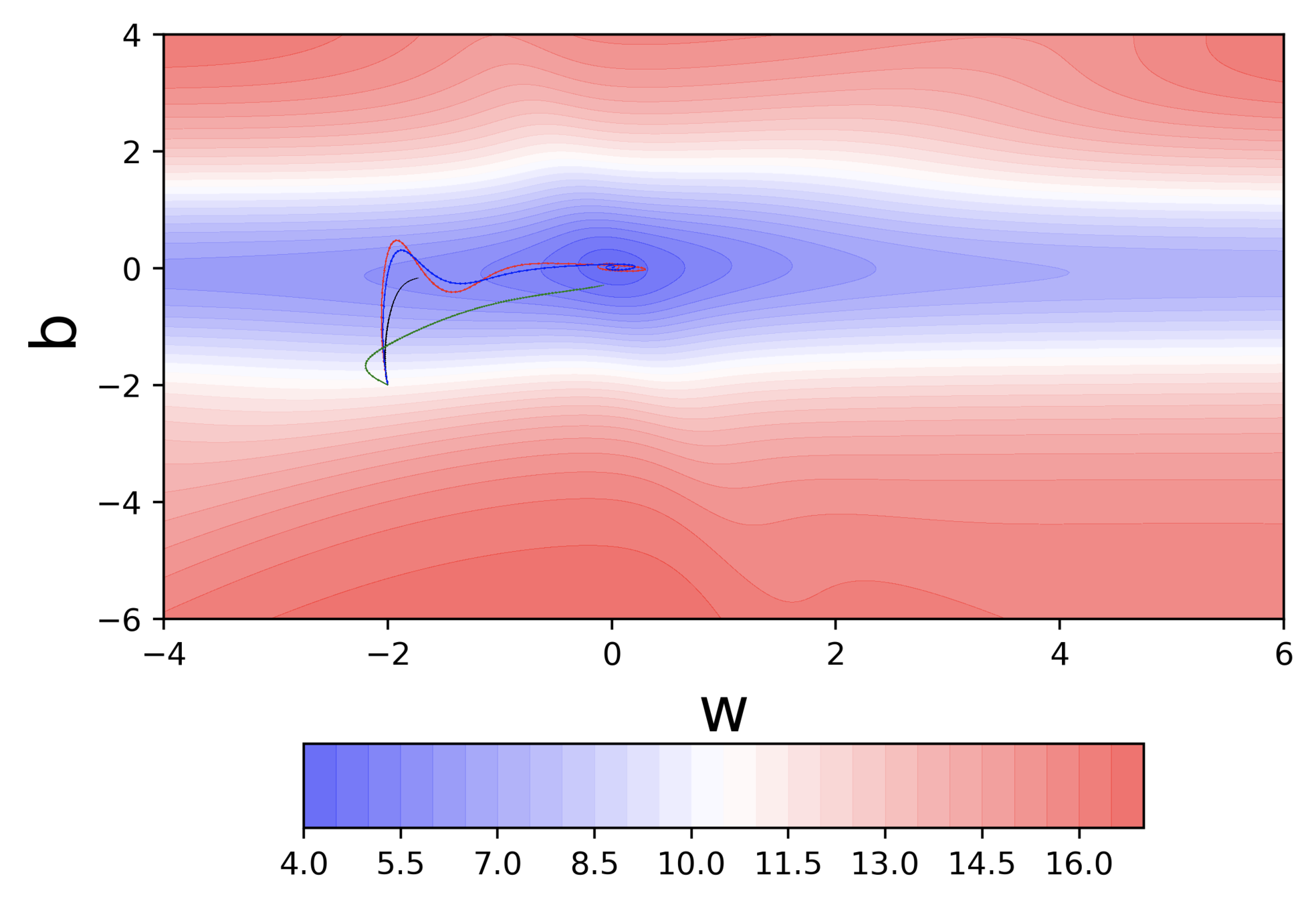
Momentum based GD

 

Would there be cases where momentum could be detrimental ?

Momentum based GD

 

What are some observations that we make ?

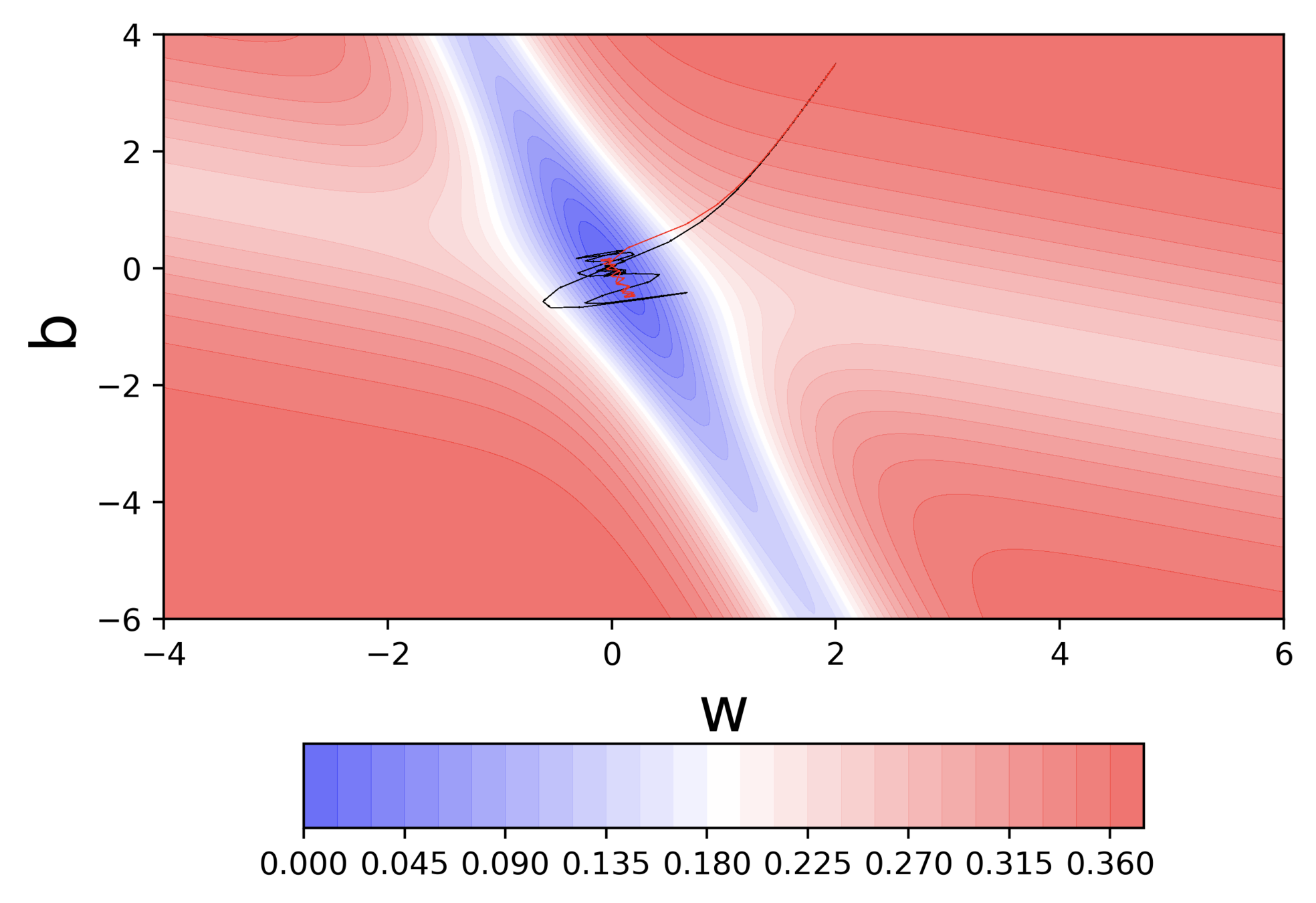
  • Momentum based gradient descent oscillates in and out of the minima valley  (u-turns)

 

  • Despite these u-turns it still converges faster than vanilla gradient descent

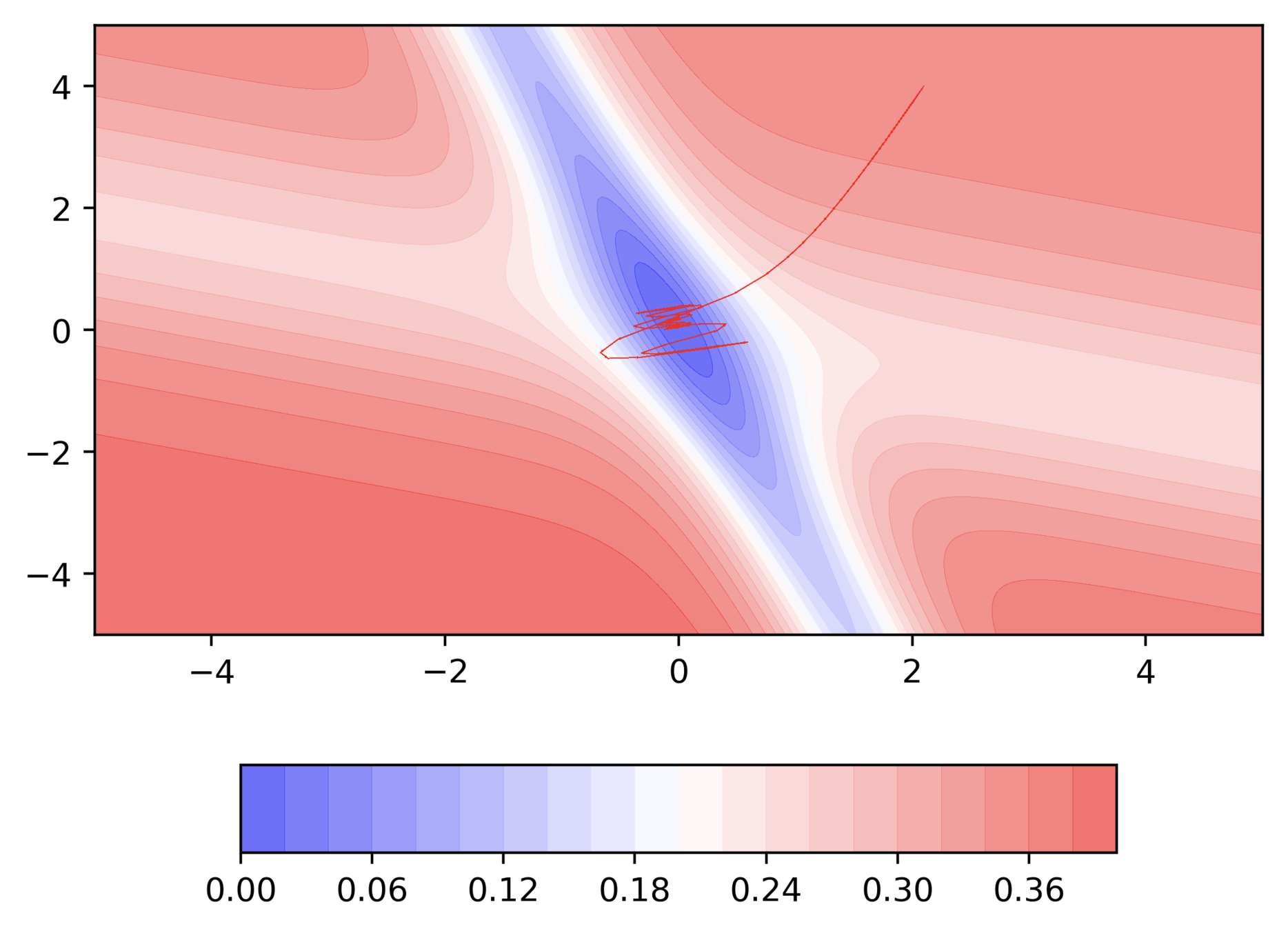
Momentum based GD

 

Can we see this from a different perspective ?

Momentum based GD

 

​Some more insights into what is happening

  • On x-axis you have epoch number, on y-axis you have \delta w value as pulses. Now you have a trend line which shows the exponentially decaying average.

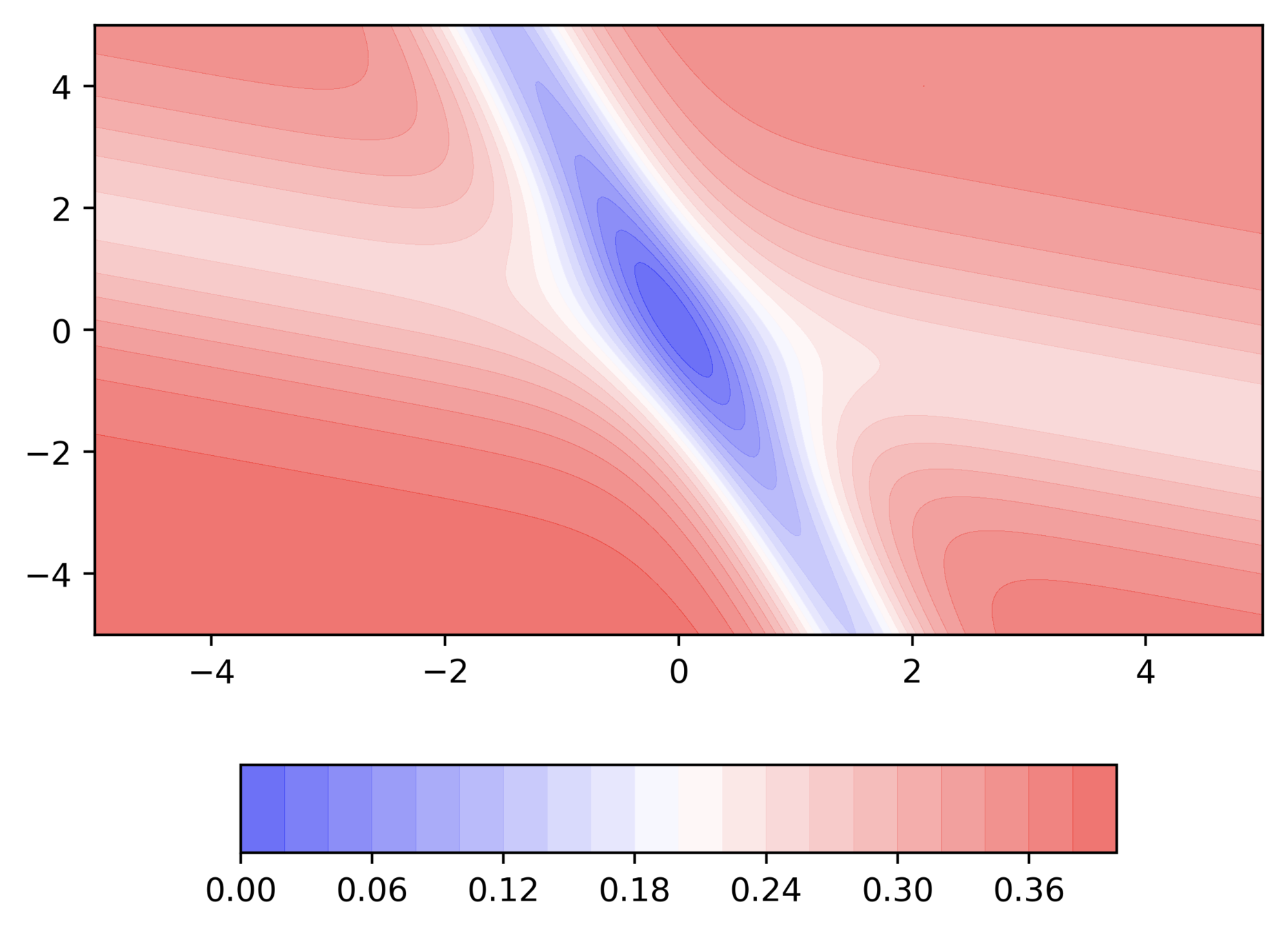
Nesterov Accelerated GD

 

Can we do something to reduce the oscillations in Momentum based GD ?

Momentum based Gradient Descent Update Rule

\begin{aligned} w_{t+1} &= w_t - \gamma * v_{t-1} - \eta \nabla w_{t} \end{aligned}
\begin{aligned} w_{temp} &= w_{t} - \gamma * v_{t-1} \\ w_{t+1} &= w_{temp} - \eta \nabla w_{temp} \\ v_t &= \gamma * v_{t-1} + \eta \nabla w_{temp} \\ \end{aligned}

NAG Update Rule

\begin{aligned} v_t &= \gamma * v_{t-1} + \eta \nabla w_t \\ w_{t+1} &= w_t - v_t \end{aligned}

Nesterov Accelerated GD

 

Can we try to understand the equations in terms of the loss surface ?

\begin{aligned} w_{t+1} &= w_t - \gamma * v_{t-1} - \eta \nabla w_{t} \end{aligned}
\begin{aligned} w_{temp} &= w_{t} - \gamma * v_{t-1} \\ w_{t+1} &= w_{temp} - \eta \nabla w_{temp} \\ v_t &= \gamma * v_{t-1} + \eta \nabla w_{temp} \\ \end{aligned}

NAG Update Rule

Nesterov Accelerated GD

 

Let's see the code for this

X = [0.5, 2.5]
Y = [0.2, 0.9]
def f(w, b, x):
   #sigmoid with parameters w, b
   return 1.0 / (1.0 + np.exp(-(w*x + b))
def error(w, b):
     err = 0.0
     for x, y in zip(X, Y): 
        fx = f(w, b, x)
        err += 0.5* (fx - y) ** 2
     return err
def grad_b(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx)

def do_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
        w = w - eta * dw
        b = b - eta * db 
             
def grad_w(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx) * x

def do_nag_gradient_descent():
    w, b, eta, max_epochs = -2, -2, 1.0, 1000
    v_w, v_b, gamma = 0, 0, 0.9
    for i in range(max_epochs):
        dw, db = 0, 0

        #Compute the lookahead value
        w = w - gamma*v_w
        b = b - gamma*v_b

        for x, y in zip(X, Y) :
            #Compute derivatives using the lookahead value
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)

        #Now move further in the direction of that gradient
        w = w - eta * dw
        b = b - eta * db

        #Now update the history
        v_w = gamma * v_w + eta * dw
        v_b = gamma * v_b + eta * db
\begin{aligned} w_{temp} &= w_{t} - \gamma * v_{t-1} \\ w_{t+1} &= w_{temp} - \eta \nabla w_{temp} \\ v_t &= \gamma * v_{t-1} + \eta \nabla w_{temp} \\ \end{aligned}

NAG Update Rule

Nesterov Accelerated GD

 

Let's run this code

def do_nag_gradient_descent():
    w, b, eta, max_epochs = -2, -2, 1.0, 1000
    v_w, v_b, gamma = 0, 0, 0.9
    for i in range(max_epochs):
        dw, db = 0, 0

        #Compute the lookahead value
        w = w - gamma*v_w
        b = b - gamma*v_b

        for x, y in zip(X, Y) :
            #Compute derivatives using the lookahead value
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)

        #Now move further in the direction of that gradient
        w = w - eta * dw
        b = b - eta * db

        #Now update the history
        v_w = gamma * v_w + eta * dw
        v_b = gamma * v_b + eta * db

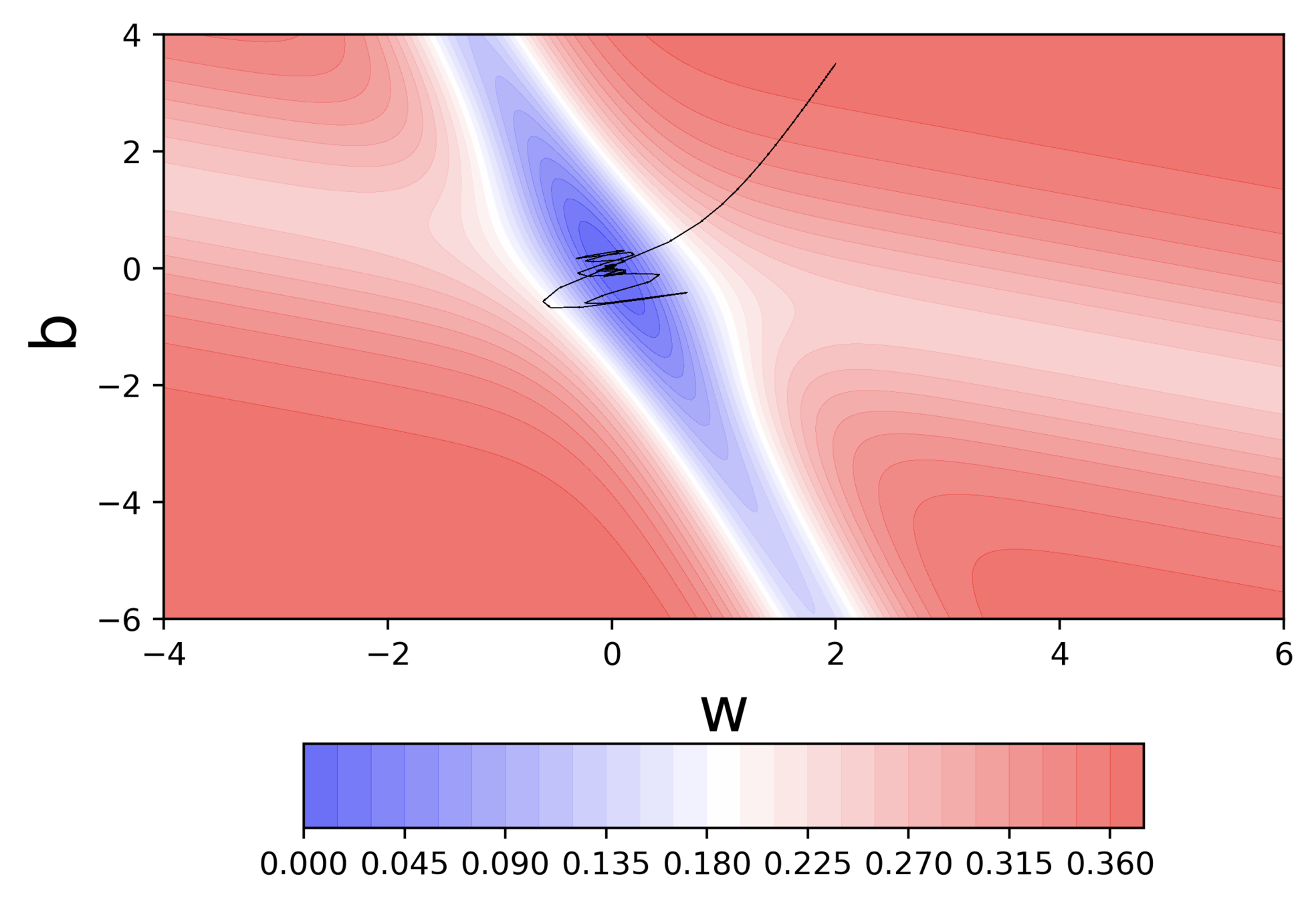
Nesterov Accelerated GD

 

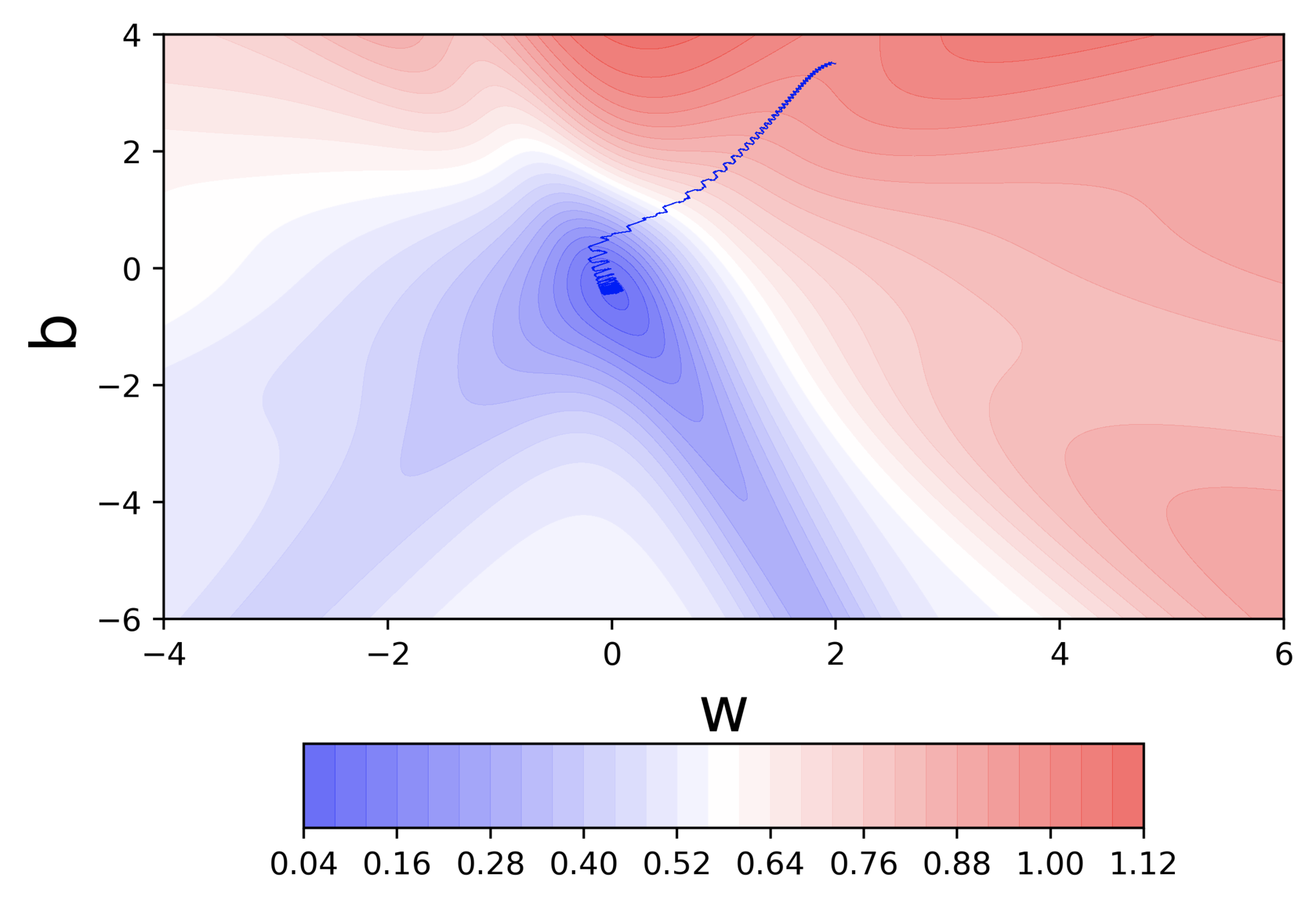
What are some observations that we make ?

  • Looking ahead helps NAG in correcting its course quicker than momentum based gradient descent

 

  • Hence the oscillations are smaller and the chances of escaping the minima valley also smaller

The Role of Learning Rate

 

​Could we not have overcome the limitation of GD by increasing the learning rate

 

It would be good to have a learning rate which could adjust to the gradient!

Better Learning algorithms

 

What are we going to see in this chapter ?

 

How do you use the gradients?

or

Can you come up with a better update rule ?

w = w - \eta \frac{\partial \mathscr{L}(w)}{\partial w}

Gradient Descent Update Rule

How do you compute the gradients ?

or

What data should you use for computing the gradients?

Batch, Stochastic and Mini-Batch GD

 

How many updates are we making ?

X = [0.5, 2.5]
Y = [0.2, 0.9]
def f(w, b, x):
   #sigmoid with parameters w, b
   return 1.0 / (1.0 + np.exp(-(w*x + b))
def error(w, b):
     err = 0.0
     for x, y in zip(X, Y): 
        fx = f(w, b, x)
        err += 0.5* (fx - y) ** 2
     return err
def grad_b(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx)

def do_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
        w = w - eta * dw
        b = b - eta * db 
             
def grad_w(w, b, x, y):
    fx = f(w, b, x)
    return (fx - y) * fx * (1 - fx) * x
\begin{aligned} \mathscr{L} = \sum_{i = 1}^{i=N}(f(x_i) - y_i)^2 \\~\\ \Delta w = \frac{\partial \mathscr{L}}{\partial w} = \sum_{i = 1}^{i=N}\frac{\partial}{\partial w} (f(x_i) - y_i)^2 \end{aligned}

Batch, Stochastic and Mini-Batch GD

 

Can we make stochastic updates?

def do_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
        w = w - eta * dw
        b = b - eta * db 
             
def do_stochastic_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
            w = w - eta * dw
            b = b - eta * db

Advantage

  • Quicker updates
  • Many updates in one pass of the data

 

Disadvantage

  • Approximate (stochastic) gradient
  • Almost like tossing a coin only once and computing the value of P(heads)

Batch, Stochastic and Mini-Batch GD

 

How is this different from Batch GD ?

Batch, Stochastic and Mini-Batch GD

 

Doesn't it make sense to use more than one point or a mini-batch of points?

def do_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
        w = w - eta * dw
        b = b - eta * db 
             
def do_stochastic_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
            w = w - eta * dw
            b = b - eta * db 
             
def do_mini_batch_gradient_descent():
    w, b, eta = -2, -2, 1.0
    max_epochs = 1000
    mini_batch_size = 0
    num_points_seen = 0
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
            num_points_seen += 1
            
            if num_points_seen % mini_batch_size == 0:
                w = w - eta * dw
                b = b - eta * db

Batch, Stochastic and Mini-Batch GD

 

How does this perform when compared to stochastic SGD ?

  • Even with a batch size of k=2 the oscillations have reduced slightly.
  • We now have slightly better estimates of the gradient
  • The higher the value of k the more accurate are the estimates

Batch, Stochastic and Mini-Batch GD

 

What is an epoch and what is a step ?

  • 1 epoch = one pass over the entire data
  • 1 step = one update of the parameters
  • N = number of data points
  • B = mini-batch size
Algorithm # of steps in one epoch
Batch gradient descent 1
Stochastic gradient descent N
Mini-Batch gradient descent N/B

Batch, Stochastic and Mini-Batch GD

​Can we have stochastic versions of NAG and Momentum based SGD ?

def do_nag_gradient_descent():
    w, b, eta, max_epochs = -2, -2, 1.0, 1000
    v_w, v_b, gamma = 0, 0, 0.9
    for i in range(max_epochs):
        dw, db = 0, 0

        #Compute the lookahead value
        w = w - gamma*v_w
        b = b - gamma*v_b

        for x, y in zip(X, Y) :
            #Compute derivatives using the lookahead value
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)

        #Now move further in the direction of that gradient
            w = w - eta * dw
            b = b - eta * db

        #Now update the history
            v_w = gamma * v_w + eta * dw
            v_b = gamma * v_b + eta * db

             
def do_stochastic_momentum_gradient_descent():
    w, b, eta, max_epochs = -2, -2, 1.0, 1000
    v_w, v_b = 0, 0
    for i in range(max_epochs):
        dw, db = 0, 0
        for x, y in zip(X, Y) :
            dw += grad_w(w, b, x, y)
            db += grad_b(w, b, x, y)
            v_w = gamma*v_w + eta * dw
            v_b = gamma*v_b + eta * db

            w = w - v_w
            b = b - v_b

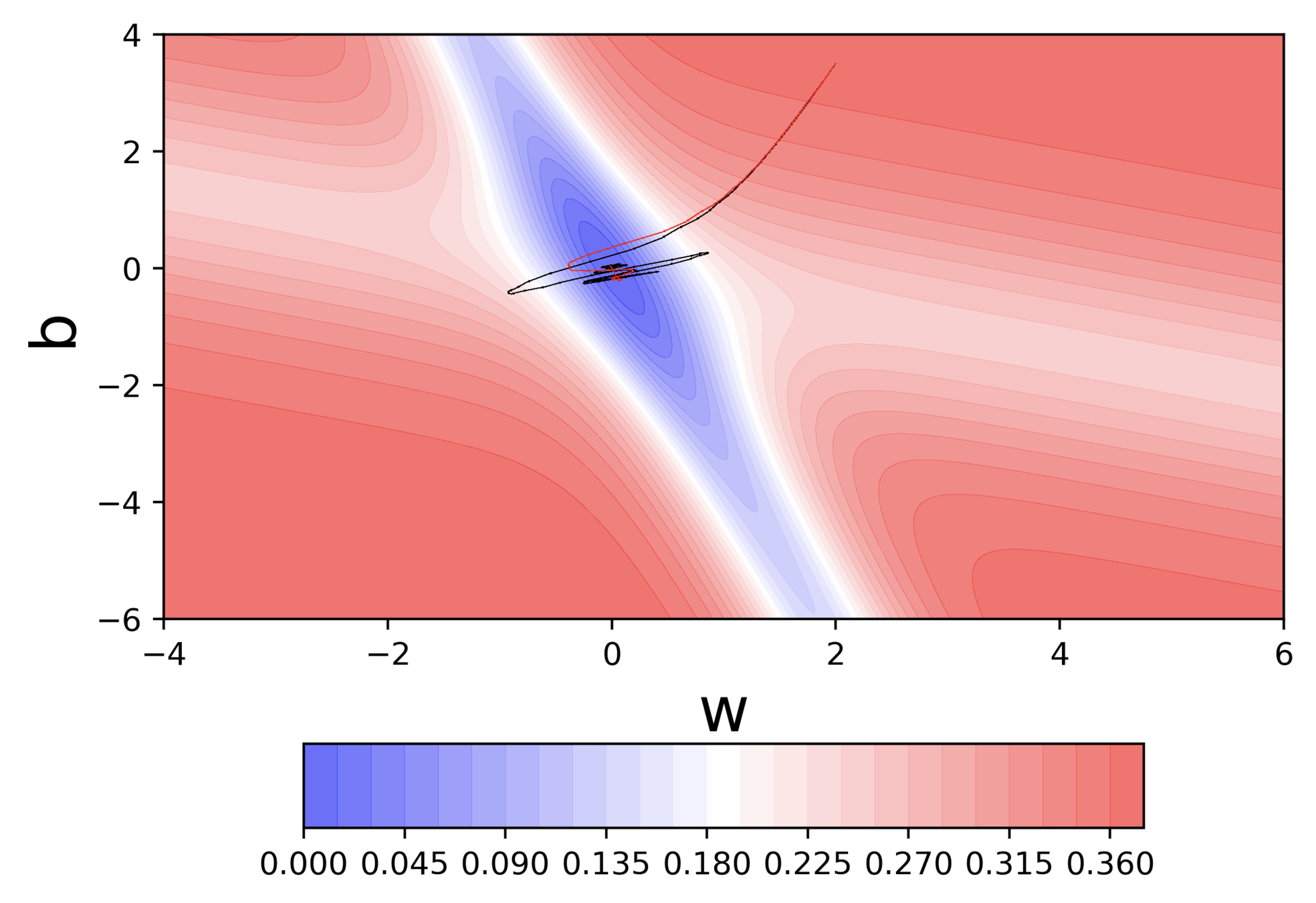
Batch, Stochastic and Mini-Batch GD

 

How do the stochastic versions of the 3 algorithms look like ?

Better Learning algorithms

 

What are we going to see in this chapter ?

 

How do you use the gradients?

or

Can you come up with a better update rule ?

w = w - \eta \frac{\partial \mathscr{L}(w)}{\partial w}

Gradient Descent Update Rule

How do you compute the gradients ?

or

What data should you use for computing the gradients?

Adaptive Learning Rate

 

Why do we need a different learning rate for every feature ?

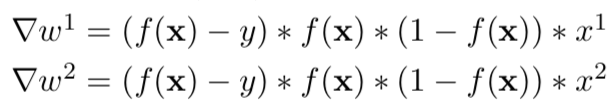
Can we have a different learning rate for each parameter which takes care of the frequency of features ?

Adaptive Learning Rate

How do we convert this intuition into an equation ?

Intuition: Decay the learning rate for parameters in proportion to their update history (fewer updates, lesser decay)

\begin{aligned} v_t &= v_{t-1} + (\nabla w_t)^2 \\ w_{t+1} &= w_t - \frac{\eta}{\sqrt{(v_t)} + \epsilon}\nabla w_t \end{aligned}

Adagrad

Adaptive Learning Rate

Let's compare this to vanilla, momentum based, nesterov gradient descent

Adaptive Learning Rate

 

What do we observe ?

Advantage

  • Parameters corresponding to sparse features get better updates


Disadvantage

  • The learning rate decays very aggressively as the  denominator grows (not good for parameters corresponding to dense features)

Adaptive Learning Rate

 

How do you convert this intuition into an equation?

Intuition: Why not decay the denominator and prevent its rapid growth ?

\begin{aligned} v_t &= \beta * v_{t-1} + (1 - \beta)(\nabla w_t)^2 \\ w_{t+1} &= w_t - \frac{\eta}{\sqrt{(v_t)} + \epsilon}\nabla w_t \end{aligned}
\begin{aligned} v_t &= v_{t-1} + (\nabla w_t)^2 \\ w_{t+1} &= w_t - \frac{\eta}{\sqrt{(v_t)} + \epsilon}\nabla w_t \end{aligned}

Adagrad

RMSProp

Adaptive Learning Rate

How does this compare to Adagrad ?

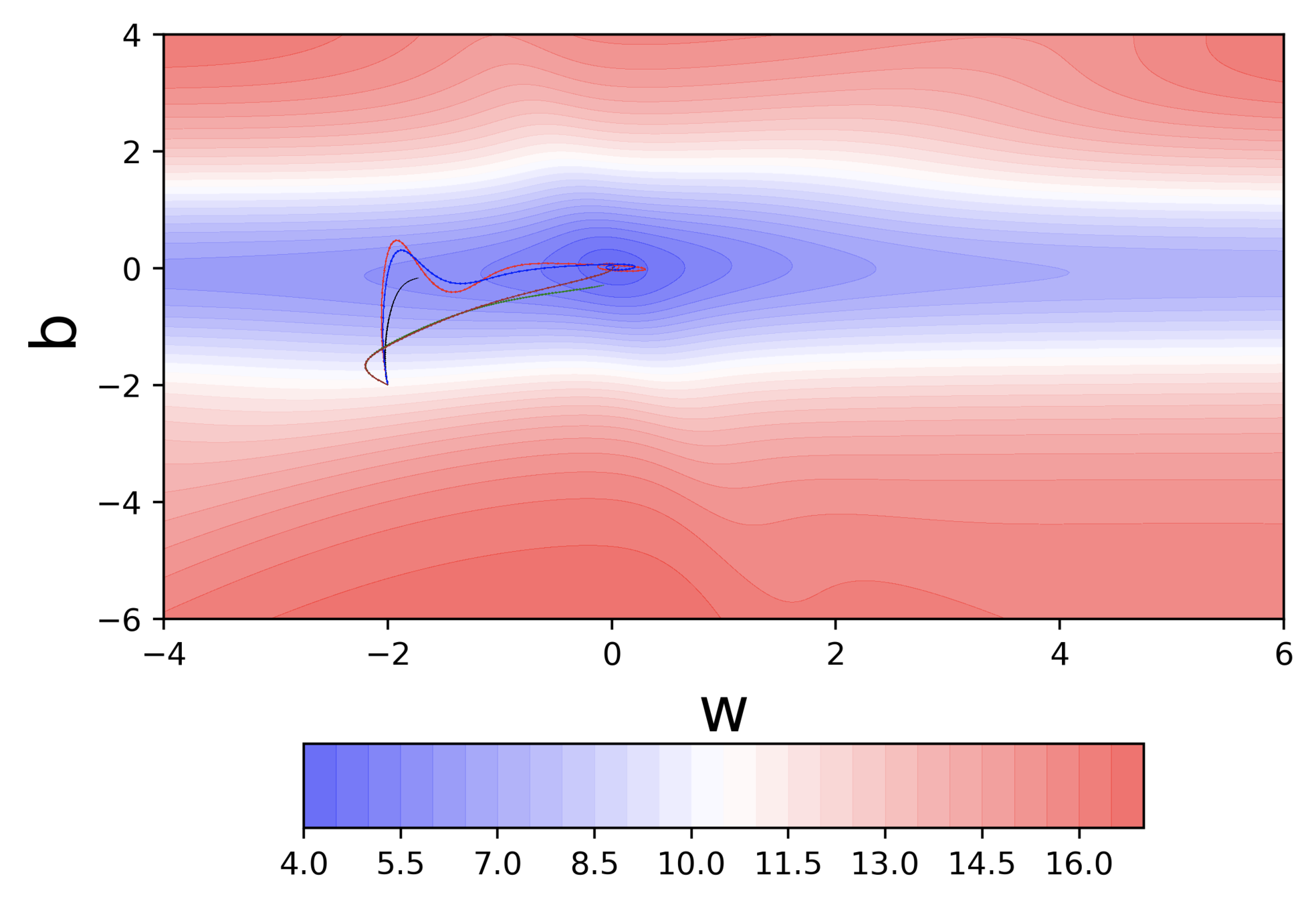
  • Adagrad got stuck when it was close  to convergence (it was no longer able to move in the vertical (b) direction because of the decayed learning rate)

 

  • RMSProp overcomes this problem by being less aggressive on the decay

Adaptive Learning Rate

 

Does it make sense to use a cumulative history of gradients ?

\begin{aligned} v_t &= \gamma * v_{t-1} + \eta \nabla w_{t} \\ w_{t+1} &= w_t - v_t \end{aligned}

Momentum based Gradient Descent Update Rule

\begin{aligned} v_t &= \beta * v_{t-1} + (1 - \beta)(\nabla w_t)^2 \\ w_{t+1} &= w_t - \frac{\eta}{\sqrt{(v_t)} + \epsilon}\nabla w_t \end{aligned}

RMSProp

Adam

\begin{aligned} m_t &= \beta_1 * v_{t-1} + (1 - \beta_1)(\nabla w_t) \\ v_t &= \beta_2 * v_{t-1} + (1 - \beta_2)(\nabla w_t)^2 \\ w_{t+1} &= w_t - \frac{\eta}{\sqrt{(v_t)} + \epsilon} m_t \end{aligned}
\begin{aligned} m_t &= \frac{m_t}{1 - \beta_1^t} \\ v_t &= \frac{v_t}{1 - \beta_2^t} \end{aligned}

Adaptive Learning Rate

 

How does this perform compared to RMSProp ?

Take-aways

Which algorithm do we use in practice ?

(c) One Fourth Labs

Algorithms

  • GD
  • Momentum based GD
  • Nesterov Accelerated GD
  • AdaGrad
  • RMSProp
  • Adam

Strategies

  • Batch
  • Mini-Batch (32, 64, 128)
  • Stochastic

Initialise 

\(w, b \)

Iterate over data:

\(w_{111} = w_{111} - \eta \Delta w_{111} \)

till satisfied

compute ~ \hat{y}
compute ~ \mathscr{L}(w, b)

\(w_{112} = w_{112} - \eta \Delta w_{112} \)

\(w_{313} = w_{313} - \eta \Delta w_{313} \)

....

\color{red}= \left\{\begin{array}{lr} & \\ & \\ & \end{array}\right\}
Made with Slides.com