What is Statistics?
What are some of the topics that we study in Statistics?
What is the role of Probability Theory in Statistics?
Learning Objectives




collect
process
store
describe
model
Recap: What is Data Science?
Knowledge of Statistics is required for collecting, processing, describing and modelling data!
Statistics is the science of collecting, describing and drawing inferences from data



collect
describe
model
What is Statistics?

model
drawing inferences
*The purpose of modelling here is to draw inferences about the data (underlying distribution, relationships, etc.
























Key Terms and Definitions
In Statistics we are always, interested in studying a large collection of people or objects

Opinion Poll: What proportion of the citizens support candidate XYZ ?
Challenge: Infeasible (expensive) to survey all citizens
























In Statistics we are always, interested in studying a large collection of people or objects

Car Testing: What is the average mileage of cars produced in a factory?
Challenge: Expensive to test all cars
Key Terms and Definitions
In Statistics we are always, interested in studying a large collection of people or objects

Survey: Is there a lot of variation in the yield of paddy farms in a state?
Challenge: Not enough resources to survey all farms
Key Terms and Definitions
























Solution: Survey only a few elements and draw inferences about all elements from this smaller group



Key Terms and Definitions




A population is the total collection of all objects that we are interested in studying

A sample is a subgroup of the population that we study to draw inferences about the population
Population
Sample
Key Terms and Definitions

We are typically interested in estimating some parameter of the population
- proportion of citizens in favour of a candidate
Key Terms and Definitions

- average mileage of cars produced in a factory

- variance in the yield of farms in a state

This quantity estimated from a small sample is called a statistic
- proportion, mean, median, standard deviation, variance when computed from a sample is called a statistic
Key Terms and Definitions






A parameter is any numeric property of the entire population under study

A statistic is any numerical property of the sample of a population which is used as an estimate for the corresponding parameter of the population
Population
Sample
Key Terms and Definitions
parameter
statistic



Population
Sample
Key Terms and Definitions
parameter
statistic
These are the four most fundamental concepts in Statistics

In the remaining slides we will go over a series of questions that we will answer in this course

Population
Sample
How to select a sample?
What if we select a sample containing only university students?

What if we select a sample containing all cars produced in Unit1 (and none from the other 4 units)
What if we select farms which are near to a city and hence easier to reach?

Population
Bad Sample
How to select a sample?
What if we select a sample containing only university students?

Such a sample will not be representative of the population

A sample and the resulting statistic will be useful only if it is representative of the population

Population
Sample
How to select a sample?
Simple random sampling
What will you learn in this course?


Stratified Sampling



Cluster Sampling


How to design an experiment to collect data?




select a group of volunteers/subjects
measure their cholesterol level today
ask them to consume 5 walnuts/day for 3 mths
measure their cholesterol after 3 months
How do you go about answering this question?

Does eating 5-7 walnuts a day for 3 months reduce cholesterol level?
How to design an experiment to collect data?




What if some members take up physical exercise and hence their cholesterol level decreases?
What is wrong with the above approach?
What if some members take up smoking and hence their cholesterol level increases?
Does eating 5-7 walnuts a day for 3 months reduce cholesterol level?
How to design an experiment to collect data?





While studying the effect of one variable (walnut) on another (cholesterol level) we must ensure that we nullify the effect of lurking variables (smoking, exercise, etc.)
Does eating 5-7 walnuts a day for 3 months reduce cholesterol level?
How to design an experiment to collect data?




Does eating 5-7 walnuts a day for 3 months reduce cholesterol level?
Randomised control experiments
What will you learn in this course?
explanatory, response and lurking variables

treatments, control groups, placebo

single blind and double blind experiments

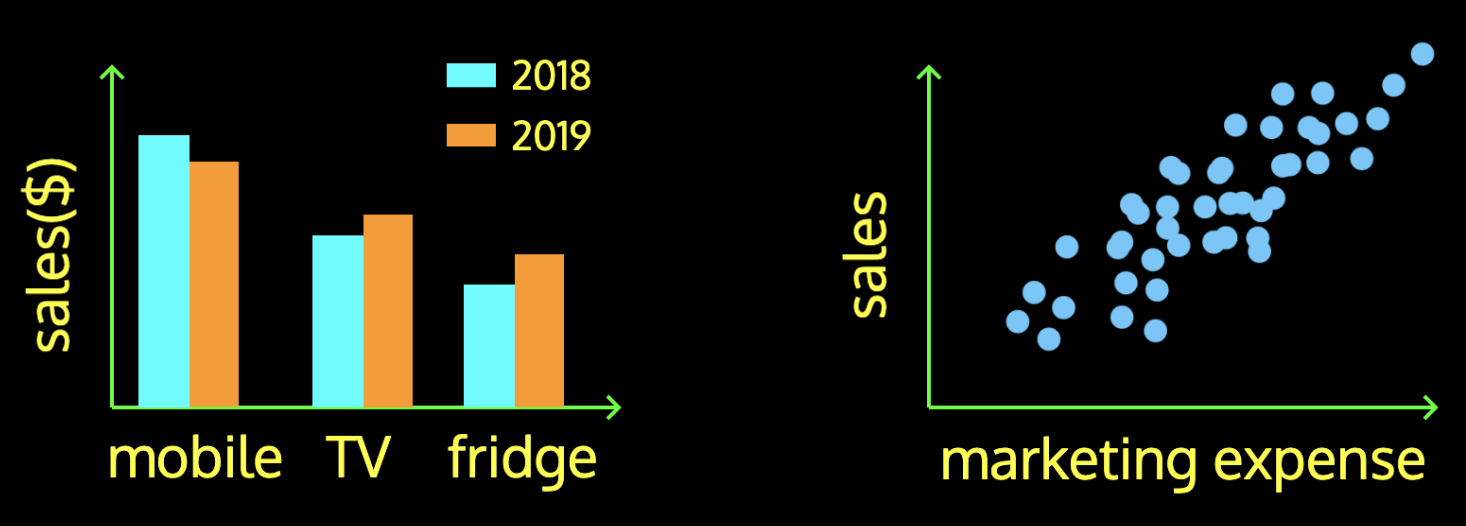
How to describe and summarise data?

How do I analyse Netflix users' data?

| User Id | Age Group | # of hours per month |
|---|---|---|
| 00001 | 20-25 | 21 |
| 00002 | 30-35 | 15 |
| 00003 | 30-35 | 31 |
| ... ... ... | ... ... ... | ... ... ... |
| 04000 | 20-25 | 41 |
4000 rows

How to describe and summarise data?
| User Id | Age Group | # of hours per month |
|---|---|---|
| 00001 | 20-25 | 21 |
| 00002 | 30-35 | 15 |
| 00003 | 30-35 | 31 |
| ... ... ... | ... ... ... | ... ... ... |
| 04000 | 20-25 | 41 |

In this tabular format it is very difficult answer even simple questions
What is the minimum/maximum number of hours that a user in the 20-25 age group spend on watching TV shows?
Are there more users in the lower range (10-15 hours per month) or in the higher range (80-90 hours per month) ?
Is the data clustered at the centre (most users in the 45-50 hours range and very few at the the 2 extremes) ?
How to describe and summarise data?

Drawing plots and computing summary statistics allows us to quickly get a feel for the data
5 50 100
(hours)
mean
median
mode
std. deviation
variance
How to describe and summarise data?

How do I analyse Netflix users' data?


Descriptive Statistics
What will you learn in this course?
(relative) frequency charts, frequency polygons, histograms, stem-and-leaf plots, box plots, scatter plots, etc.

measures of centrality and spread

Why do we need Probability Theory?



A sampling strategy is said to be truly random (unbiased) if every element in the population has an equal chance of becoming a part of the sample

Population
Good Sample
Bad Sample
Why do we need Probability Theory?


What do we mean by chance?

The branch of Mathematics that deals with chances and probabilities is called Probability Theory

Population
Good Sample
Bad Sample
Why do we need Probability Theory?
In how many different ways can you create a sample of size 2 from a population of size 10?
Population (10 elements)










Sample (2 elements)


(90 ways)
If you observe some trend in this small sample what is the chance that you will observe a similar trend in other samples or the entire population!

Why do we need Probability Theory?
Population (10K elements)








Sample (100 elements)


(6.5*10^241 ways)
If you estimate a mean from this small sample what is the chance that the mean of the entire population is close to this mean!

... ... ...

... ... ...

Why do we need Probability Theory?
Population (10K elements)








Sample (100 elements)


... ... ...

... ... ...

Introduction to Probability Theory
What will you learn in this course?
sample spaces, event, axioms of probability

discrete and continuous random variables

Bernoulli, Uniform and Normal distribution

How do we give guarantees for estimates made from a sample?
Population (10 students)










Diff. Samples (2 students)










1
2
3
4
5
Estimated mean height
130
148
152
156
175
How do we give guarantees for estimates made from a sample?
Diff. Samples (2 students)








1
2
3
... ...
90
The mean itself has a probability distribution (different values of the mean have different chances of being observed)
130
148
152
156
175

... ...

mean height
How do we give guarantees for estimates made from a sample?
Diff. Samples (2 students)








1
2
3
... ...
90
... ...
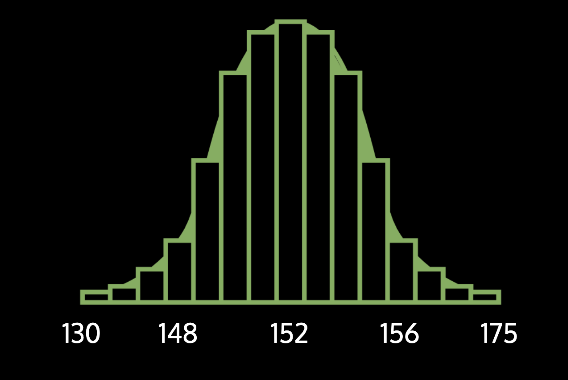
if the mean computed from a single sample is x can you give an interval such that you are 95% sure that the mean of the population lies in this interval

Point Estimate
Interval Estimate
How do we give guarantees for estimates made from a sample?
Diff. Samples (2 students)








1
2
3
... ...
90
... ...
What will you learn in this course?

point estimates

distributions of sampling statistics

interval estimates

What is a hypothesis and how do we test it?







100
85
87
90
98
Bumrah bowling speed (mph)
81
Hypothesis: The mean bowling speed of Bumrah is greater than 90 mph
What's the big deal? I can see from the sample that this is true!
Caveat: We are estimating from a sample (what if Bumrah got lucky and this sample was good)
What is a hypothesis and how do we test it?






100
85
87
90
98
Bumrah bowling speed (mph)
81
Recall: the mean itself has a distribution (different samples, different means)

I reject the hypothesis that the mean speed of Bumrah is greater than 90 mph because there is a 25% chance that I might get a sample in which the mean speed is greater than 90 mph even if the true mean is less than 95 mph

85
100
70
What is a hypothesis and how do we test it?
Hypothesis (two populations): The mean yield per acre by using fertiliser X is greater than fertiliser Y






Fertiliser X




Fertiliser Y
I reject the hypothesis because there is a 20% chance that I might get a sample in which the mean yield of fertiliser X is greater than fertiliser Y even when that is not true for the population

What is a hypothesis and how do we test it?
Hypothesis (multiple populations): A vegan diet with a yoga based workout is most effective for improving fitness
| Yoga | Cross fit | |
|---|---|---|
| Vegan | ||
| Vegetarian | ||
| Non-vegetarian |
























What is a hypothesis and how do we test it?
| Yoga | Cross fit | |
|---|---|---|
| Vegan | ||
| Vegetarian | ||
| Non-vegetarian |
























Hypothesis testing
What will you learn in this course?

single population, two populations, multiple populations

z-tests, t-tests, Analysis of Variance (ANOVA)
How to model relationships between variables?




What is the relationship between number of days of treatment and cholesterol level?
Statistical modelling
y = mx + c
decrease in cholesterol level
number of days of treatment
Assume a simple relationship between the variables
How to model relationships between variables?



# of days of treatment
decrease in cholesterol

Estimate parameters (m and c) from data
| Patient Id | # of days of treatment | decrease in cholesterol |
|---|---|---|
| 00001 | 75 | 15 |
| 00002 | 90 | 25 |
| ... ... ... ... | ... ... ... ... | ... ... ... ... |
| 00100 | 45 | -5 |
Statistical modelling
How to model relationships between variables?



# of days of treatment
decrease in cholesterol

Deal with uncertainty (remember m and c are estimated from a sample, not population)
Are we 99% sure that the value of m estimated from this sample lies within a small neighbourhood around the true value of m?

Statistical modelling
How to model relationships between variables?



# of days of treatment
decrease in cholesterol

Linear Regression
What will you learn in this course?

estimating parameters

estimating confidence bands

measuring goodness-of-fit
How wells does the model fit the data?


Hypothesis: In cricket, the five ways* of getting dismissed are equally likely
* ignoring rarer ways of getting dismissed
0.2
Probability
caught . lbw . bowled stumped run out .
Probability
Model
How well does this model fit the data?
How wells does the model fit the data?


Estimate probabilities from data (say last 100 dismissals: sample)
* ignoring rarer ways of getting dismissed
caught . lbw . bowled stumped run out .
Estimated from data
How well does this model fit the data?
0.2
Probability
How wells does the model fit the data?

* ignoring rarer ways of getting dismissed
caught . lbw . bowled stumped run out .
Estimated from data
Are the variations observed in the sample significant or due to random chance?
0.2
Probability
0.2
Probability
caught . lbw . bowled stumped run out .
Probability
Model
How wells does the model fit the data?

0.2
Probability
caught . lbw . bowled stumped run out .
Probability
Model
Chi-square test
What will you learn in this course?
determine goodness-of-fit

determine if 2 variables are independent

List of Topics
Descriptive Statistics
Probability Theory
Inferential Statistics
Different types of data
Different types of plots
Measures of centrality and spread
Sample spaces, events, axioms
Discrete and continuous RVs
Bernoulli, Uniform, Normal dist.
Sampling strategies
Interval Estimators
Hypothesis testing (z-test, t-test)
ANOVA, Chi-square test
Linear Regression
























What is Statistics? Key Terms



























































What is Statistics? Key Terms


































