Recap: List of Topics
Descriptive Statistics
Probability Theory
Inferential Statistics
Different types of data
Different types of plots
Measures of centrality and spread
Counting, Sample spaces, events
Discrete and continuous RVs
Bernoulli, Uniform, Normal dist.
Sampling strategies
Point and Interval Estimators
Hypothesis testing (z-test, t-test)
ANOVA, Chi-square test
Distribution of Sample Statistics
Recap: List of Topics
Descriptive Statistics
Probability Theory
Inferential Statistics
Different types of data
Different types of plots
Measures of centrality and spread
Counting, Sample spaces, events
Discrete and continuous RVs
Bernoulli, Uniform, Normal dist.
Sampling strategies
Point and Interval Estimators
Hypothesis testing (z-test, t-test)
ANOVA, Chi-square test
Distribution of Sample Statistics
Point and Interval Estimators
Learning objectives
- Apply ideas from distribution of sample statistics
- Definition, properties of estimators
- Point estimators of mean, variance, proportion
- Interval estimators of mean
- when population variance is known
- when population variance is unknown
to estimate population parameters
Where are we?
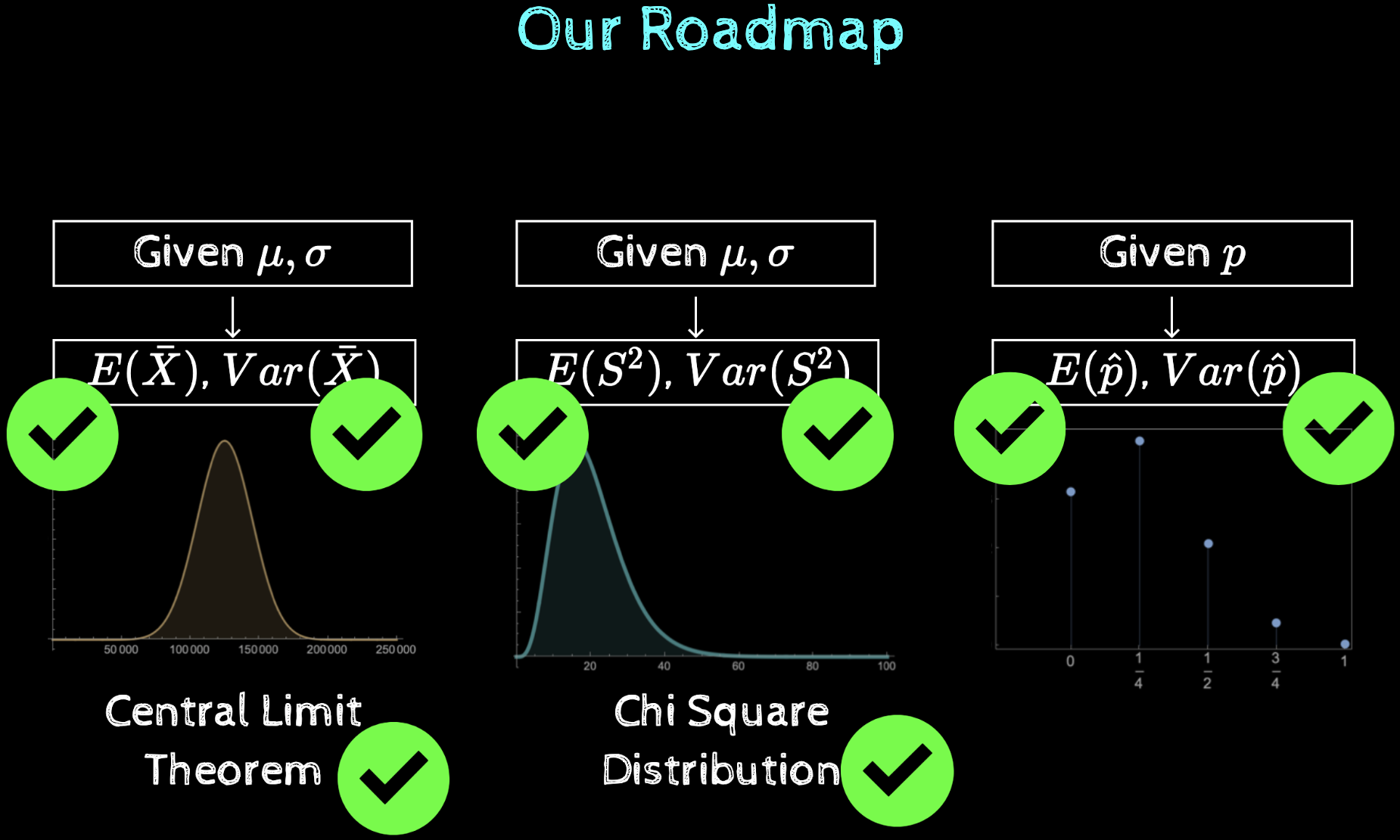
Where are we, really?

We have built up lot of potential energy with the knowledge of distribution of sample statistics
It is now time to apply it for solving problems of practical interest
Only in theory, we study distribution of statistics over all or many samples
In practice, we often have a single sample and want to infer things
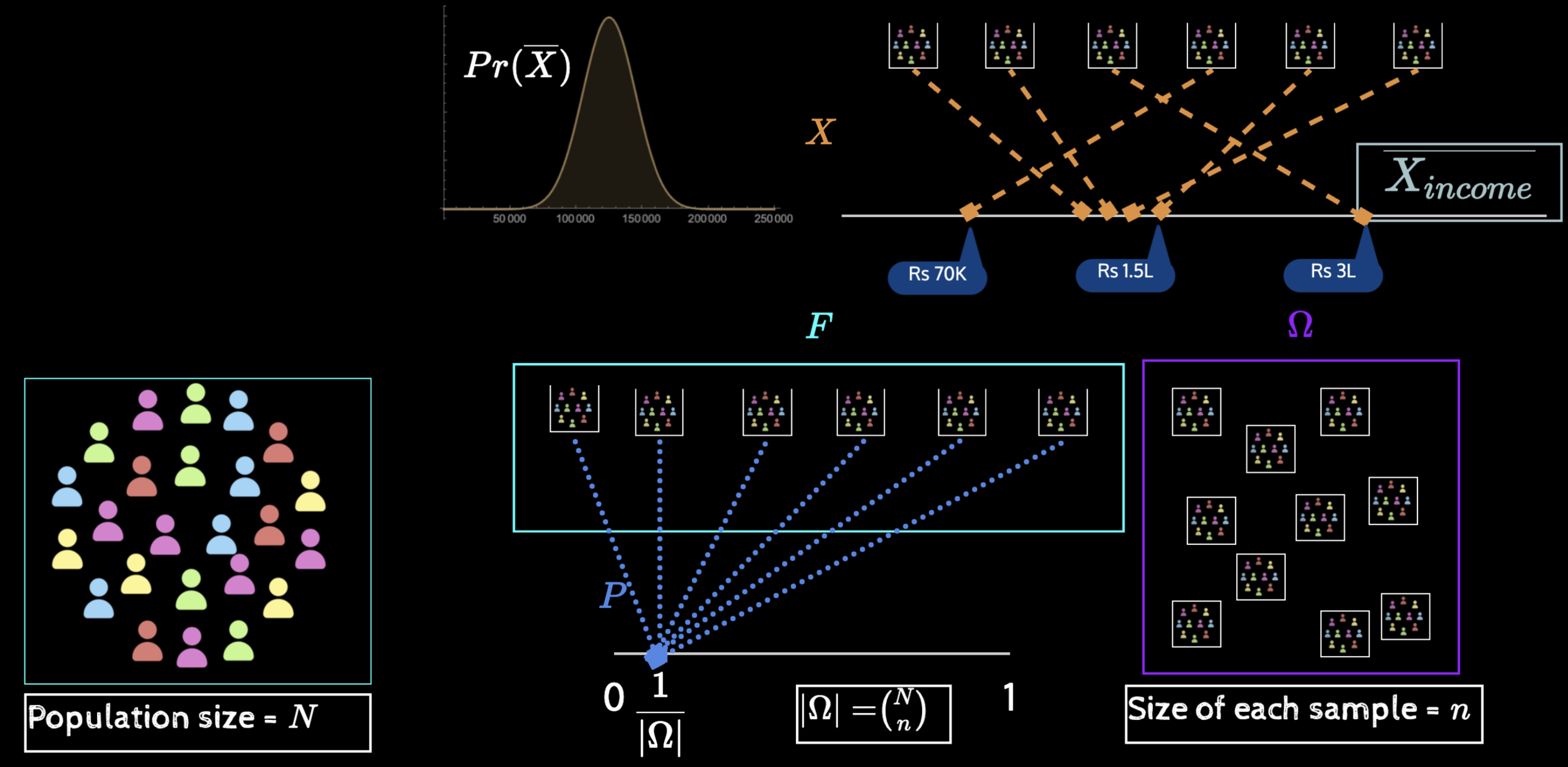
More seriously
\(\mu_{income}, \sigma_{income}\)


Given population parameters
Find distribution of sample statistics

More seriously
\(\mu_{income}, \sigma_{income}\)


Estimate population parameters
Given some
sample data
Our ideas of distr. of sample statistics
+
Main results so far
\(\mathbb{E}[\overline{X}] = \mu\)
\(\mathbb{E}[\hat{p}] = p\)
\(\mathrm{var}(\hat{p}) \) \(= \frac{p(1-p)}{n}\)
\(\mathrm{var}[\overline{X}] = \frac{\sigma^2}{n}\)
\(\mathbb{E}[S^2_{n-1}] = \sigma^2\)
For all population distributions
For population with normal distribution
\(\frac{\overline{X} - \mu}{\sigma} \sim \mathcal{N}(0, 1)\)
\(\frac{(n-1){S^2_{n-1}}}{\sigma^2} \sim \chi(n-1)\)
Sample questions
Scores of Sachin in a tournament that I saw
28
120
38
27
111
2
53
85
18
What is his career average? How sure are we?
Sample questions
My daily weight logged over a week
If we know the error of the weighing scale, what can we say about my weight?

72.5
74.5
73
74
72
73.5
74
Sample questions
"Do you program as a hobby?"
Responses by 64,416 developers
Source: StackOverflow
What are the error margins?

General Template
We have some sample data
We would like to infer about the entire population
Step 1: Compute sample statistics
Step 2: Use knowledge of distribution of sample statistics
Step 3: Estimate population parameters
What is an estimator
28
120
38
27
111
2
53
85
18
Observed data
Calculate \(\overline{X}\)
Rule or function
Estimator
\(\overline{X} = 53.6\)
Value
Estimate
\(\mu\)
Population parameter
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
What is an estimator
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
28
120
38
27
111
2
53
85
18
Observed data
Calculate \(\overline{X}\)
\(\overline{X} = 61.2\)
\(\mu\)
52
36
81
152
50
98
5
97
15
83
4
Rule or function
Estimator
Value
Estimate
Population parameter
What is an estimator
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
0
1
2
-4
-3
-2
-1
3
4
Point estimate
"We estimate that \(\mu\) is 1.5"
What is an estimator
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
0
1
2
-4
-3
-2
-1
3
4
Interval Estimate
"We estimate that \(\mu\) is in the interval [0.5, 3]"
What is an estimator
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
0
1
2
-4
-3
-2
-1
3
4
Interval Estimate
What if we take the entire number line?
Not useful
We want intervals to be narrow
What is an estimator
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
0
1
2
-4
-3
-2
-1
3
4
Interval Estimate
"We estimate that \(\mu\) is in the interval [0.5, 3]"
Can we be sure that it can never be outside this interval?
Usually not
What is an estimator
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
0
1
2
-4
-3
-2
-1
3
4
Interval Estimate
"We estimate that \(\mu\) is in the interval [0.5, 3] with a 95% confidence"
Confidence Interval
Properties of an Estimator
How would we like our estimator to be?
Unbiased estimator
If expected value of the estimator is equal to the parameter we are estimating
\(\mathbb{E}[\overline{X}] = \mu\)
\(\mathbb{E}[\hat{p}] = p\)
\(\mathbb{E}[S^2_{n - 1}] = \sigma^2\)
Properties of an Estimator
How would we like our estimator to be?
Unbiased estimator
Consistent estimator
As the number of sample points increases, sequence of estimates converges to the parameter
Properties of an Estimator
Consistent estimator
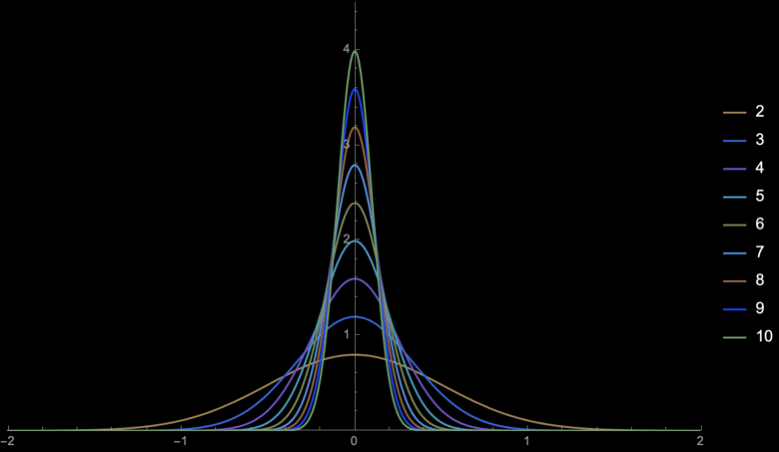
Properties of an Estimator
Consistent estimator
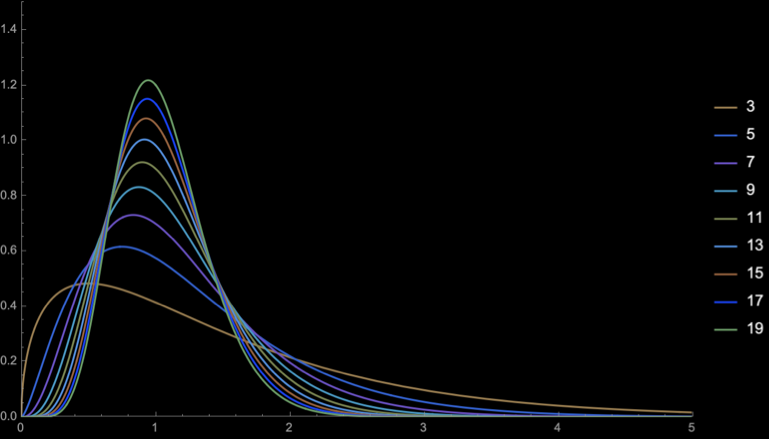
Properties of an Estimator
How would we like our estimator to be?
Unbiased estimator
Consistent estimator
As the number of sample points increases, sequence of estimates converges to the parameter
\(\mathrm{sd}(\overline{X}) = \frac{\sigma}{\sqrt{n}}\)
\(\mathrm{sd}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\)
\(\mathrm{sd}(S^2_{n - 1}) = \frac{\sqrt{2}\sigma^2}{\sqrt{n}}\)
Properties of an Estimator
How would we like our estimator to be?
Unbiased estimator
Consistent estimator
Efficient estimator
Optimal with respect to a loss function of our choice
Point Estimator of Population Mean
The sample mean as the point estimator of the population mean
\(\mathbb{E}[\overline{X}] = \mu\)
\(\mathrm{sd}(\overline{X}) = \frac{\sigma}{\sqrt{n}}\)
Unbiased estimator
"Standard error"
Point Estimator of Population Mean
Example
The height of 7 randomly chosen employees
\(\overline{X} = \frac{1167}{7} = 166.7\) cms
Can we find standard error?
No, we need population parameter \(\sigma\)
\(151, 166, 181, 155, 182, 172, 160\) cms
\(\mathbb{E}[\overline{X}] = \mu\)
\(\mathrm{sd}(\overline{X}) = \frac{\sigma}{\sqrt{n}}\)
Point Estimator of Population Mean
Example
The height of 7 randomly chosen employees
\(151, 166, 181, 155, 182, 172, 160\) cms
\(\overline{X} = \frac{1167}{7} = 166.7\) cms
Standard deviation of population is 9.2 cms
\(\mathrm{sd}(\overline{X}) = \frac{9.2}{\sqrt{7}} \approx 3.5\) cms
\(\mathbb{E}[\overline{X}] = \mu\)
\(\mathrm{sd}(\overline{X}) = \frac{\sigma}{\sqrt{n}}\)
Point Estimator of Population Proportion
The sample proportion as the point estimator of the population proportion
\(\mathbb{E}[\hat{p}] = p\)
\(\mathrm{sd}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\)
Unbiased estimator
"Standard error"
Point Estimator of Population Proportion
Example
You have an biased coin, and you want to predict the proportions of Heads in throws
H, T, H, H, T, H, T, T, H, H
The results of 10 throws are
\(\hat{p} = \frac{6}{10} = 0.6\)
No, we need population parameter \(p\)
Can we predict the standard error?
\(\mathbb{E}[\hat{p}] = p\)
\(\mathrm{sd}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\)
Point Estimator of Population Proportion
Example
You have an biased coin, and you want to predict the proportions of Heads in throws
H, T, H, H, T, H, T, T, H, H
The results of 10 throws are
\(\hat{p} = \frac{6}{10} = 0.6\)
\(\mathbb{E}[\hat{p}] = p\)
\(\mathrm{sd}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\)
\(\mathrm{sd}(\hat{p}) < \sqrt{\frac{0.5(1-0.5)}{n}} = \frac{1}{2\sqrt{n}}\)
\(\mathrm{sd}(\hat{p}) < \frac{1}{2\sqrt{10}} \approx 0.16 \)
Point Estimator of Population Proportion
Example
You have an biased coin, and you want to predict the proportions of Heads in throws
\(\mathbb{E}[\hat{p}] = p\)
\(\mathrm{sd}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\)
\(\mathrm{sd}(\hat{p}) < \sqrt{\frac{0.5(1-0.5)}{n}} = \frac{1}{2\sqrt{n}}\)
What if we wanted standard error no more than 0.05?
\(\frac{1}{2\sqrt{n}} = 0.05 \Rightarrow n = 100 \)
Point Estimator of Population Proportion
Example
You have an biased coin, and you want to predict the proportions of Heads in throws
\(\mathbb{E}[\hat{p}] = p\)
\(\mathrm{sd}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\)
\(\mathrm{sd}(\hat{p}) < \sqrt{\frac{0.5(1-0.5)}{n}} = \frac{1}{2\sqrt{n}}\)
What if we wanted standard error no more than 0.05?

\(\hat{p} = \frac{56}{10} = 0.56\)
\(\mathrm{sd}(\hat{p}) < \frac{1}{2\sqrt{100}} = 0.05 \)
Point Estimator of Population Variance
The sample variance as the point estimator of the population variance
Unbiased estimator
"Standard error"
\(\mathbb{E}[S^2_{n - 1}] = \sigma^2\)
\(\mathrm{sd}(S^2_{n - 1}) = \frac{\sqrt{2}\sigma^2}{\sqrt{n}}\)
Point Estimator of Population Variance
Example
You are measuring the period of a pendulum with a stop watch for 5 periods
\(2.01, 1.98, 1.96, 2.02, 2.00\ \mathrm{s}\)
\(S^2_{n - 1} = \frac{\sum_{i = 1}^n (X_i - \overline{X})^2}{n - 1} = 0.00058\ \mathrm{s}^2\)
We can use the above to estimate the standard deviation \(S = 0.024 \ \mathrm{s}\)
Point Estimator of Population Variance
Example
You are measuring the period of a pendulum with a stop watch for 5 periods
\(2.01, 1.98, 1.96, 2.02, 2.00\ \mathrm{s}\)
\(S^2_{n - 1} = \frac{\sum_{i = 1}^n (X_i - \overline{X})^2}{n - 1}\)
We don't compute standard error of variance
Point Estimator of Population Variance
Example
You are measuring the period of a pendulum with a stop watch for 5 periods
\(2.01, 1.98, 1.96, 2.02, 2.00\ \mathrm{s}\)
\(S^2_{n - 1} = \frac{\sum_{i = 1}^n (X_i - \overline{X})^2}{n - 1}\)
Had we known \(\mu\), would you use a different esimtator?
Exercise
Point Estimator of Population Variance
Example
You are measuring the period of a pendulum with a stop watch for 5 periods
\(2.01, 1.98, 1.96, 2.02, 2.00\ \mathrm{s}\)
\(S^2_{n - 1} = \frac{\sum_{i = 1}^n (X_i - \overline{X})^2}{n - 1}\)
Let \(\mu = 2\ \mathrm{s}\)
\(S^2_\mu = \frac{\sum_{i = 1}^n (X_i - \mu)^2}{n} = 0.0005\ \mathrm{s}^2\)
Corresponding standard deviation \( = 0.022\ \mathrm{s}\)
Point Estimator of Population Variance
\(S^2_{n - 1} = \frac{\sum_{i = 1}^n (X_i - \overline{X})^2}{n - 1}\)
\(S^2_\mu = \frac{\sum_{i = 1}^n (X_i - \mu)^2}{n}\)
How do these estimators differ?
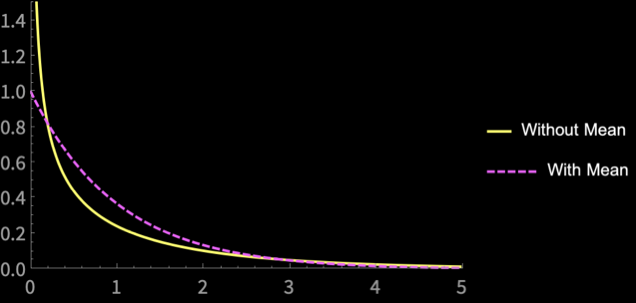
\(n = 2\)
Point Estimator of Population Variance
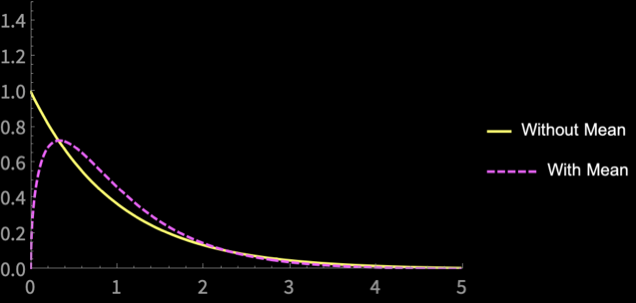
\(n = 3\)
Point Estimator of Population Variance
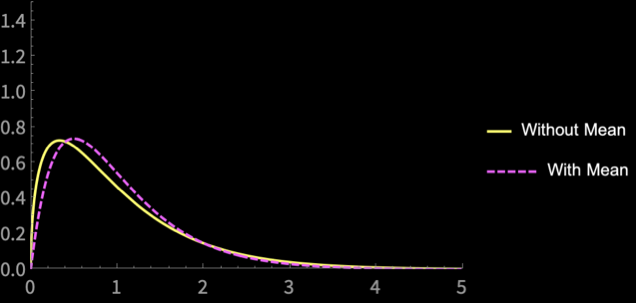
\(n = 4\)
Point Estimator of Population Variance
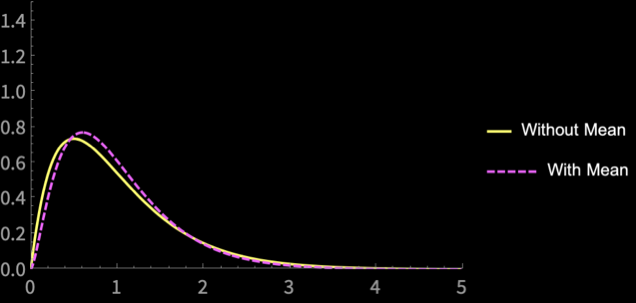
\(n = 5\)
Point Estimator of Population Variance
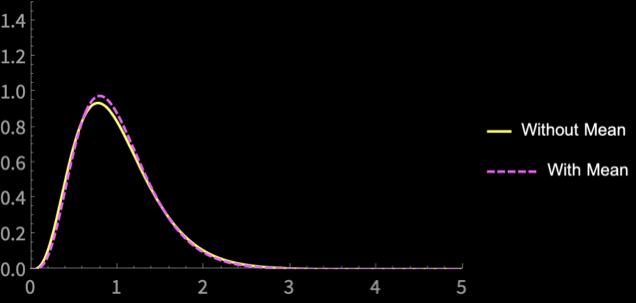
\(n = 10\)
Point Estimator of Population Variance
\(n = 20\)
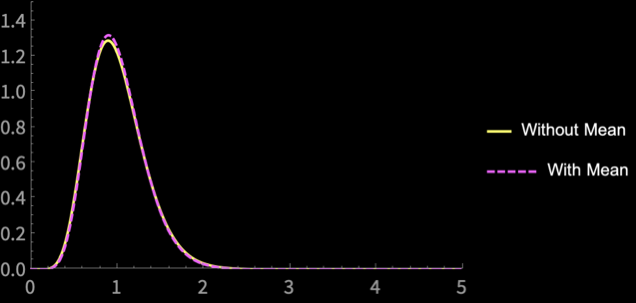
Point Estimator of Population Variance
Point Estimator of Population Variance
\(S^2_{n - 1} = \frac{\sum_{i = 1}^n (X_i - \overline{X})^2}{n - 1}\)
\(S^2_\mu = \frac{\sum_{i = 1}^n (X_i - \mu)^2}{n}\)
If we know \(\mu\), we should use it
Disadvantage is small for large \(n\)
Real World Problem
Consider the prices of Bitcoin from March 2020 to August 2020
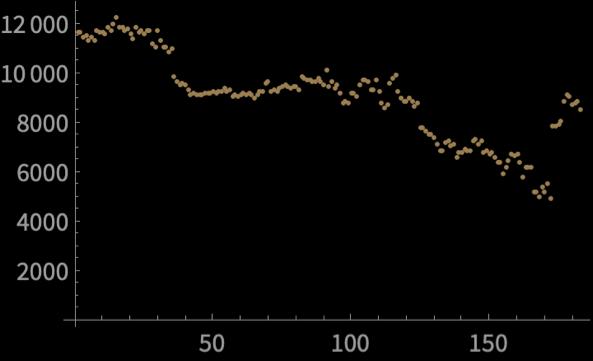
Price in USD
One point per day
\(n = 183\)
Real World Problem
Consider the prices of Bitcoin from March 2020 to August 2020

We will assume a linear random walk model
\(x_{d}[n] = x[n + 1] - x[n]\)
We will assume that \(x_d\) are randomly distributed with a normal distribution
Real World Problem
Consider the prices of Bitcoin from March 2020 to August 2020

\(x_{d}[n] = x[n + 1] - x[n]\)
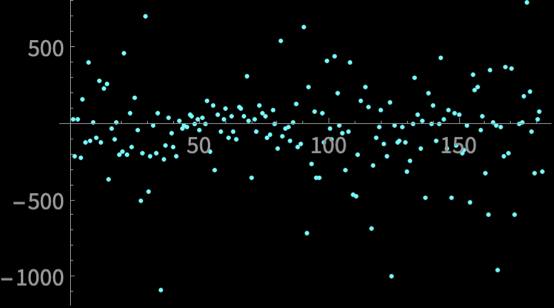
Real World Problem
Consider the prices of Bitcoin from March 2020 to August 2020

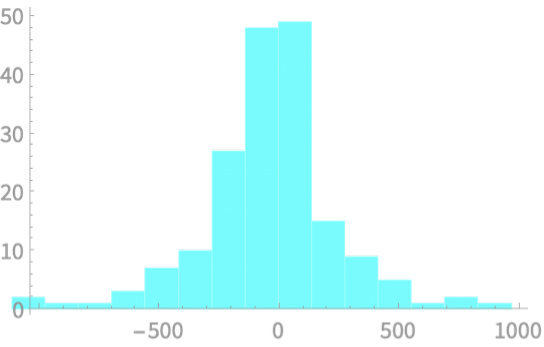
\(x_{d}[n] = x[n + 1] - x[n]\)

Real World Problem
Consider the prices of Bitcoin from March 2020 to August 2020


\(x_{d}[n] = x[n + 1] - x[n]\)

Compute sample variance and use that to estimate population variance
\(S^2_{n - 1} = 124743\)
\(S \approx 353\) USD
Real World Problem
Consider the prices of Bitcoin from March 2020 to August 2020
\(x_{d}[n] = x[n + 1] - x[n]\)
We can also try scaling the differences
\(x_{r}[n] = \frac{x[n + 1] - x[n]}{x[n]}\)
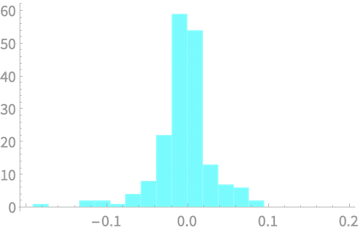
Another Real World Problem
Consider infant weight measurement
\(3.75, 3.25, 2.5, 2.5, 3.5, 3.25, 3, 2.5, 2.25, 3.25 \ \mathrm{kg}\)
We have the following measurements for 10 children born on a date
We have used a weighing scale with standard deviation of \(250\ \mathrm{g}\)
What is the variance of the weights of children?
Another Real World Problem
Consider infant weight measurement
Std dev of weighing scale = \(250\ \mathrm{g}\)
Weight measured = Weight of child + Error
var(weight measured) = var(weight of child) + var(error)
\(0.256\) = var(weight of child) + \(0.25^2\)
var(weight of child) = \(0.1936\)
\(3.75, 3.25, 2.5, 2.5, 3.5, 3.25, 3, 2.5, 2.25, 3.25 \ \mathrm{kg}\)
sd(weight of child) = \(0.44\ \mathrm{kgs}\)
On to interval estimators
An estimator is a statistic of a given sample. The value of the estimator, called an estimate is used to predict a population parameter
0
1
2
-4
-3
-2
-1
3
4
Interval Estimator
"We estimate that \(\mu\) is in the interval [0.5, 3] with a 95% confidence"
Confidence Interval
Formally
Interval Estimator
The confidence of this estimate is the probability that the population parameter is contained within this interval.
An interval estimator of a population parameter predicts an interval which is expected to contain the parameter.
Interval Estimator of Population Mean
We cannot study this in the general case
We will only study the case of a normal population
With known population variance
With unknown population variance
Interval Estimator of \(\mu\)
with known \(\sigma\)
0
1
2
-4
-3
-2
-1
3
4
Confidence Interval
What do we need for this?
The distribution of \(\overline{X}\)
Interval Estimator of \(\mu\)
with known \(\sigma\)
The distribution of \(\overline{X}\)
What do we know about this for a normal population with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)
We know that \(Z\) is a standard normal variable
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)
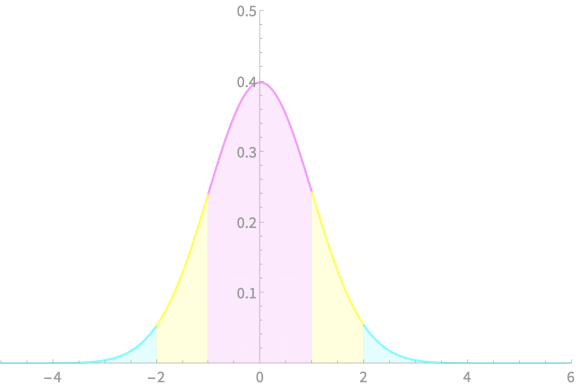
\(\mathrm{Pr}(|Z| < 1) \approx 0.68\)
\(\mathrm{Pr}(|Z| < 2) \approx 0.96\)
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)
\(\mathrm{Pr}(|Z| < 1) \approx 0.68\)
\(\mathrm{Pr}(|Z| < 2) \approx 0.96\)
\(\mathrm{Pr}(|\frac{\overline{X} - \mu}{\sigma/\sqrt{n}}| < 1) \approx 0.68\)
\(\mathrm{Pr}(\overline{X} - \frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + \frac{\sigma}{\sqrt{n}}) \approx 0.68\)
\(\mathrm{Pr}(\overline{X} - \frac{2\sigma}{\sqrt{n}} < \mu < \overline{X} + \frac{2\sigma}{\sqrt{n}}) \approx 0.96\)
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)
\(\mathrm{Pr}(\overline{X} - \frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + \frac{\sigma}{\sqrt{n}}) \approx 0.68\)
If you are given a sample of data, we can calculate \(\overline{X}\)
We can then use \(\sigma\) and \(n\) to estimate this interval
\(\overline{X}\)
\(\overline{X} + \frac{\sigma}{\sqrt{n}}\)
\(\overline{X} - \frac{\sigma}{\sqrt{n}}\)
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)
\(\mathrm{Pr}(\overline{X} - \delta < \mu < \overline{X} + \delta) \approx p\)
\(\overline{X}\)
\(\overline{X} + \delta\)
\(\overline{X} - \delta\)
Earlier, we looked at problems where given \(\delta\) we want to predict \(p\)
Now, we will look at the reverse, given \(p\) find corresponding interval
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)
\(\mathrm{Pr}(\overline{X} - \frac{I/2}{\sigma/\sqrt{n}} < \mu < \overline{X} + \frac{I/2}{\sigma/\sqrt{n}}) \approx p\)
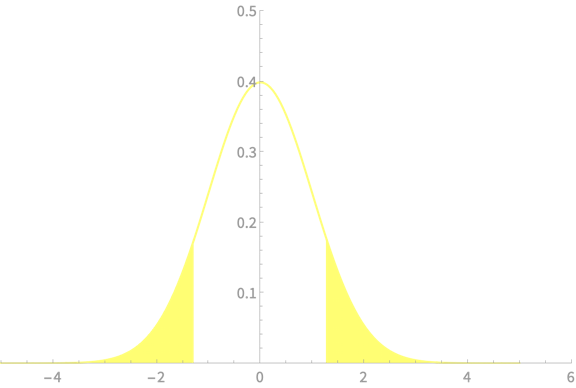
Z table lookup with \(I/2\) = \(u\)
\(p = 1 - 2u\)
\(\frac{-I}{2}\)
\(\frac{I}{2}\)
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)

Given \(p\), this area is \((1 - p)/2\)
Then \(I\) is such that z-table value for
\(-I/2\) is \((1 - p)/2\)
Since \(p\) and \(I\) are related by z-table scores, we use a different notation
\(\mathrm{Pr}(\overline{X} - \frac{I/2}{\sigma/\sqrt{n}} < \mu < \overline{X} + \frac{I/2}{\sigma/\sqrt{n}}) \approx p\)
\(\frac{-I}{2}\)
\(\frac{I}{2}\)
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(Z = \dfrac{\overline{X} - \mu}{\sigma/\sqrt{n}}\)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)

\(-z_{\alpha/2}\)
This area is \(\alpha/2\)
\(-z_{\alpha/2}\) is such that its z-table score is \(\alpha/2\)
\(z_{\alpha/2}\)
This area is \(\alpha/2\)

\(\alpha = 0.2\)
\(z_{\alpha/2} = 1.28\)
\(\mathrm{Pr}(\overline{X} - 1.28\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 1.28\frac{\sigma}{\sqrt{n}}) \approx 0.8\)
Examples
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)
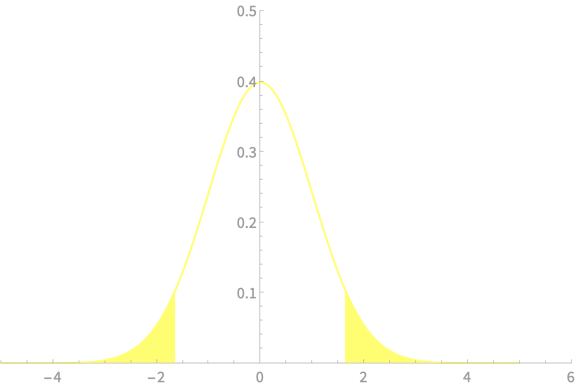
\(\alpha = 0.1\)
\(z_{\alpha/2} = 1.65\)
Examples
\(\mathrm{Pr}(\overline{X} - 1.65\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 1.65\frac{\sigma}{\sqrt{n}}) \approx 0.9\)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)
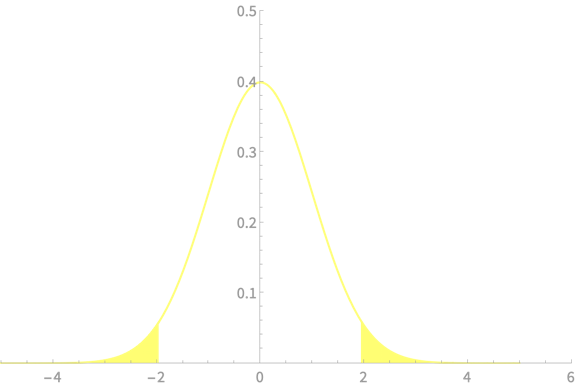
\(\alpha = 0.05\)
\(z_{\alpha/2} = 1.96\)
Examples
\(\mathrm{Pr}(\overline{X} - 1.96\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 1.96\frac{\sigma}{\sqrt{n}}) \approx 0.95\)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)
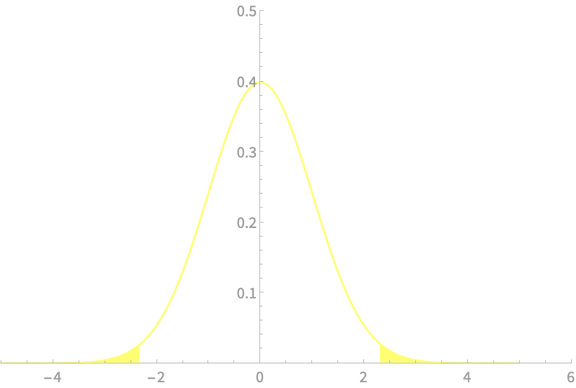
\(\alpha = 0.02\)
\(z_{\alpha/2} = 2.33\)
Examples
\(\mathrm{Pr}(\overline{X} - 2.33\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 2.33\frac{\sigma}{\sqrt{n}}) \approx 0.98\)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)
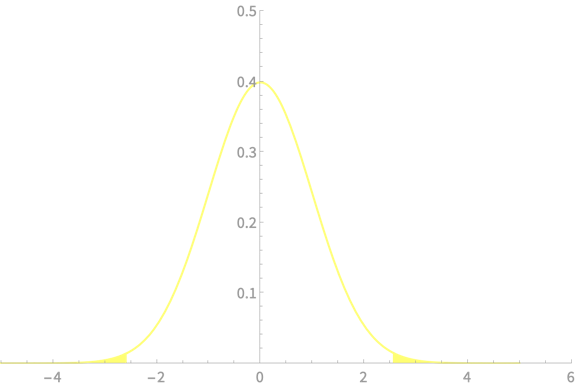
\(\alpha = 0.01\)
\(z_{\alpha/2} = 2.58\)
Examples
\(\mathrm{Pr}(\overline{X} - 2.58\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 2.58\frac{\sigma}{\sqrt{n}}) \approx 0.99\)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)
\(\alpha = 0.01\)
\(z_{\alpha/2} = 2.58\)
What does probability here mean
\(\mathrm{Pr}(\overline{X} - 2.58\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 2.58\frac{\sigma}{\sqrt{n}}) \approx 0.99\)
\(\mu\)
99 percentage of the intervals we find with different samples will contain \(\mu\)
Interval Estimator of \(\mu\)
with known \(\sigma\)
\(\alpha = 0.01\)
\(z_{\alpha/2} = 2.58\)
What does probability here mean
\(\mathrm{Pr}(\overline{X} - 2.58\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 2.58\frac{\sigma}{\sqrt{n}}) \approx 0.99\)
\(\mu\)
\(\mu\) does not change
\(\overline{X}\) changes and the probability is across different samples
Interval Estimator of \(\mu\)
with known \(\sigma\)
You visit a Mandi bazaar
Interval Estimator of \(\mu\)
with known \(\sigma\)
Different vendors are offering different prices, which vary from day to day
You know that the standard deviation across vendors is about 75 paise per kilo
How many vendors should you ask the price to be 90 percent confident within an interval of 50 paise?

Interval Estimator of \(\mu\)
with known \(\sigma\)
Interval length = \(0.5\) Re
\(\alpha = 0.1\)
\(\sigma = 0.75\) Re
\(\mathrm{Pr}(\overline{X} - 1.65\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 1.65\frac{\sigma}{\sqrt{n}}) \approx 0.9\)
\(\alpha = 0.1 \Rightarrow z_{\alpha/2} = 1.65\)
\(2 \times 1.65\frac{\sigma}{\sqrt{n}} < 0.5\)
n > 24.5
How much will your work increase if you wanted 95 percentage confidence
Interval Estimator of \(\mu\)
with known \(\sigma\)
Interval length = \(0.5\) Re
\(\alpha = 0.05\)
\(\sigma = 0.75\) Re
\(\mathrm{Pr}(\overline{X} - 1.96\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + 1.96\frac{\sigma}{\sqrt{n}}) \approx 0.95\)
\(\alpha = 0.05 \Rightarrow z_{\alpha/2} = 1.96\)
\(2 \times 1.96\frac{\sigma}{\sqrt{n}} < 0.5\)
n > 34.6
How much will your work increase if you wanted 95 percentage confidence
Lower and Upper bounds

So far we have been seeing bounds centred around a value
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) =(1 - \alpha)\)
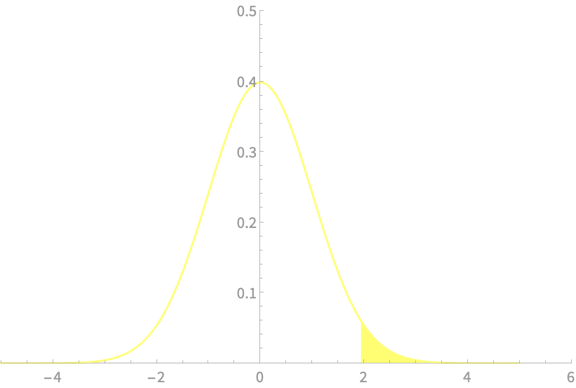
Lower and Upper bounds
We can compute the lower bound on \(\mu\) as
\(\mathrm{Pr}(\mu > \overline{X} - z_{\alpha}\frac{\sigma}{\sqrt{n}}) =(1 - \alpha)\)
This area is \(\alpha\)
Lower and Upper bounds
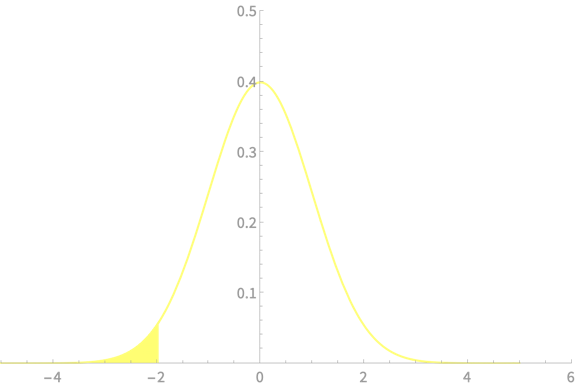
Similarly for the upper bound
\(\mathrm{Pr}(\mu < \overline{X} + z_{\alpha}\frac{\sigma}{\sqrt{n}}) =(1 - \alpha)\)
This area is \(\alpha\)
Lower and Upper bounds
\(\mathrm{Pr}(\mu < \overline{X} + z_{\alpha}\frac{\sigma}{\sqrt{n}}) =(1 - \alpha)\)
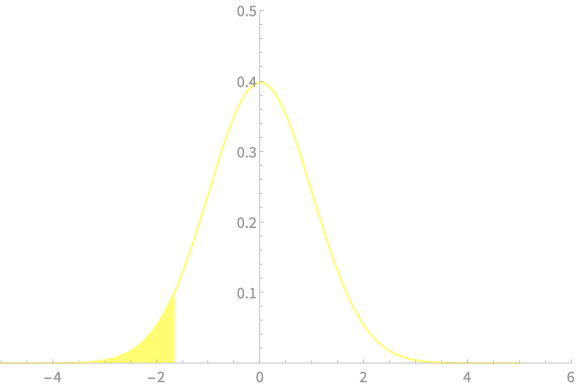

\(\alpha = 0.9, \sigma = 1, n = 25\)
\(\mu < \overline{X} + 0.33\)
\(\overline{X} - 0.39 < \mu < \overline{X} +0.39\)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) =(1 - \alpha)\)
Upper bound is tighter in the single sided case
You have PM2.5 readings for last three weeks from Hauz Khas in New Delhi
Upper Confidence Bound
You need to report the upper bound of the mean with 95 percentage confidence
We know standard deviation as 8 µg/m3

25, 28, 24, 29, 33, 36, 31, 45, 50, 36, 29, 33, 24, 24, 18, 24, 20, 25, 23, 27, 35
Upper Confidence Bound
\(\alpha = 0.05\)
\(\sigma = 8\)
25, 28, 24, 29, 33, 36, 31, 45, 50, 36, 29, 33, 24, 24, 18, 24, 20, 25, 23, 27, 35
\(\mathrm{Pr}(\mu < \overline{X} + z_{\alpha}\frac{\sigma}{\sqrt{n}}) =(1 - \alpha)\)
\(\mathrm{Pr}(\mu < 29.48 + z_{0.95}\frac{8}{\sqrt{21}}) =0.05\)
\(\mu < 32.84\)
With confidence 0.95, upper bound is 32.84 µg/m3
Interval Estimator of Population Mean
So far we have assumed we know \(\sigma\)
This is not always the case
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)
What is the natural solution?
Use \(S_{n-1}\) instead of \(\sigma\)
Interval Estimator of \(\mu\), unknown \(\sigma\)
Use \(S_{n-1}\) instead of \(\sigma\)
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
\(\sqrt{n}\frac{\overline{X} - \mu}{S_{n-1}}\)
Since we know well that we use the unbiased sample variance, we will drop the sub-script
Interval Estimator of \(\mu\), unknown \(\sigma\)
Use \(S\) instead of \(\sigma\)
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
\(\sqrt{n}\frac{\overline{X} - \mu}{S}\)
For a normal population or a large \(n\), we know that \(Z \sim \mathcal{N}(0, 1)\)
What is the distribution of this statistic?
Interval Estimator of \(\mu\), unknown \(\sigma\)
Use \(S\) instead of \(\sigma\)
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
\(\sqrt{n}\frac{\overline{X} - \mu}{S}\)
For a normal population or a large \(n\), we know that \(Z \sim \mathcal{N}(0, 1)\)
What is the distribution of this statistic?
Note that here both numerator & denominator vary with sample
Interval Estimator of \(\mu\), unknown \(\sigma\)
\(T = \sqrt{n}\frac{\overline{X} - \mu}{S}\)
\(T^2 = \frac{(\overline{X} - \mu)^2}{\frac{S^2}{n}}\)
\(= \frac{(\overline{X} - \mu)^2}{\frac{S^2}{n}} \frac{\frac{n}{\sigma^2}}{\frac{n}{\sigma^2}}\)
\(= \frac{\frac{(\overline{X} - \mu)^2}{\sigma^2/n}}{\frac{S^2}{\sigma^2}}\)
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
\(= \frac{Z^2}{\frac{S^2}{\sigma^2} \frac{n-1}{n-1}}\)
\(= \frac{Z^2/1}{[(n-1) \frac{S^2}{\sigma^2}]/(n-1)}\)
We know that this has a \(\chi^2(1)\) distribution
We know that this has a \(\chi^2(n - 1)\) distribution
Interval Estimator of \(\mu\), unknown \(\sigma\)
\(T = \sqrt{n}\frac{\overline{X} - \mu}{S}\)
\(T^2 = \frac{(\overline{X} - \mu)^2}{\frac{S^2}{n}}\)
\(= \frac{(\overline{X} - \mu)^2}{\frac{S^2}{n}} \frac{\frac{n}{\sigma^2}}{\frac{n}{\sigma^2}}\)
\(= \frac{\frac{(\overline{X} - \mu)^2}{\sigma^2/n}}{\frac{S^2}{\sigma^2}}\)
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
\(= \frac{Z^2}{\frac{S^2}{\sigma^2} \frac{n-1}{n-1}}\)
\(= \frac{Z^2/1}{[(n-1) \frac{S^2}{\sigma^2}]/(n-1)}\)
Ratio of \(\chi^2(1)\) divided by degrees of freedom
Ratio of \(\chi^2(n - 1)\) divided by degrees of freedom
This ratio is a \(F\)-distribution with degrees of freedom
\(1\) and \(n - 1\)
Interval Estimator of \(\mu\), unknown \(\sigma\)
\(T^2_{n - 1} \)
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
\(= \frac{Z^2/1}{[(n-1) \frac{S^2}{\sigma^2}]/(n-1)}\)
\(T^2_{n - 1} \sim F\)-distribution with
1 and \(n - 1\) degrees of freedom
\(T_{n - 1}\) is called the \(t\) random variable with \(n - 1\) degrees of freedom
\(T_{n - 1} = \sqrt{n}\frac{\overline{X} - \mu}{S}\)
Interval Estimator of \(\mu\), unknown \(\sigma\)
\(T_{n - 1} = \sqrt{n}\frac{\overline{X} - \mu}{S}\)
\(T_{n - 1}\) is called the \(t\) random variable with \(n - 1\) degrees of freedom
What is its PDF?
The distribution of \(T_{n - 1}\) is called the student's t-distribution
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
Student's T-distribution
\(Z = \sqrt{n}\frac{\overline{X} - \mu}{\sigma}\)
\(T_{n - 1} = \sqrt{n}\frac{\overline{X} - \mu}{S}\)
As \(n\) increases, \(S\) converges to \(\sigma\)
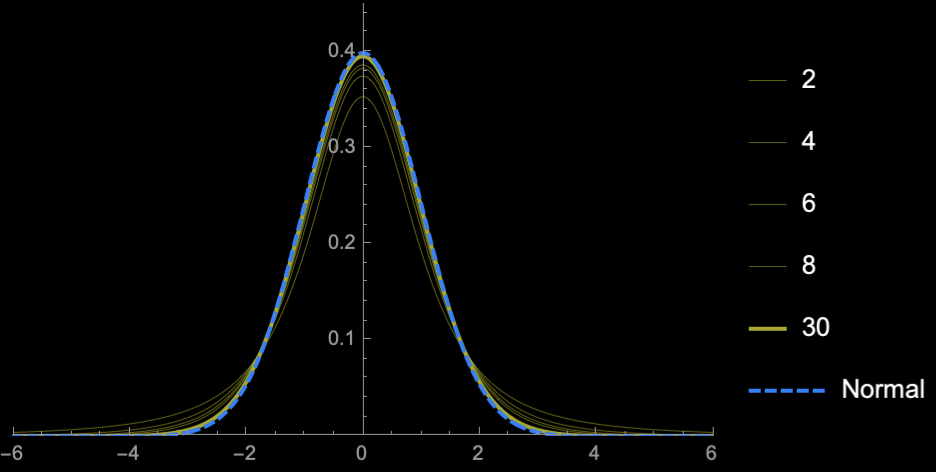
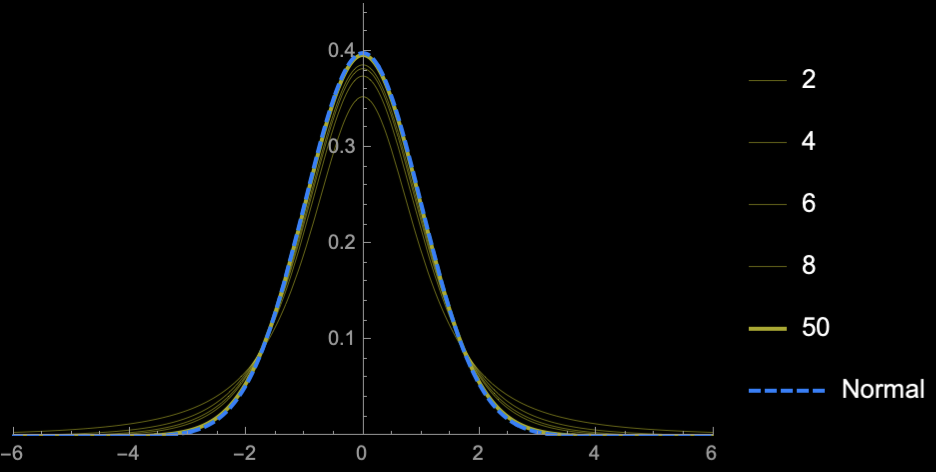
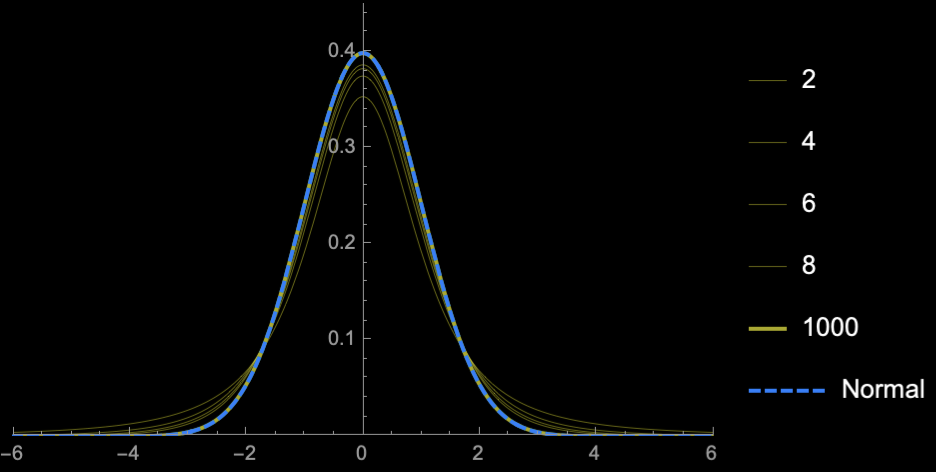
Thus, for large \(n\) the student's distribution with \(n - 1\) degrees of freedom converges to \(\mathcal{N}(0, 1)\)
The difference should be large for small values of \(n\), i.e., when studying small samples
Student's T-distribution
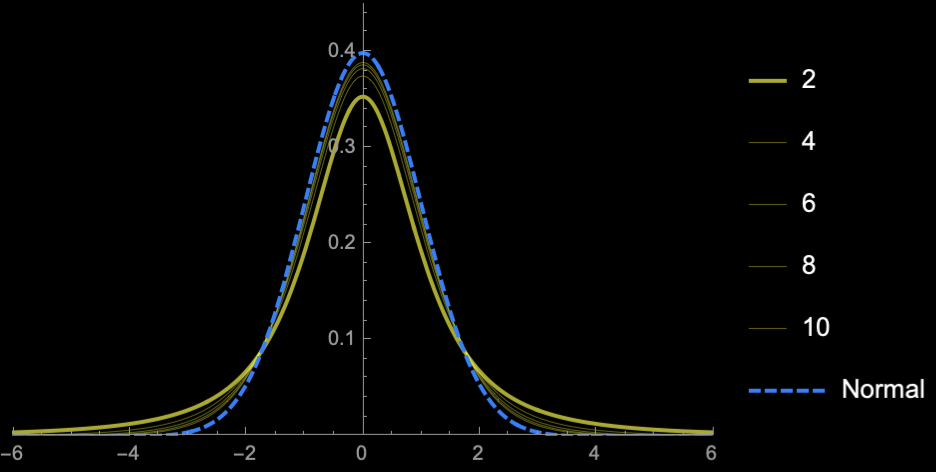
Student's \(t\)-distribution has more area under the "tails" than \(\mathcal{N}(0, 1)\)
\(\Rightarrow\) Higher uncertainty (Price of
not knowing \(\sigma\))
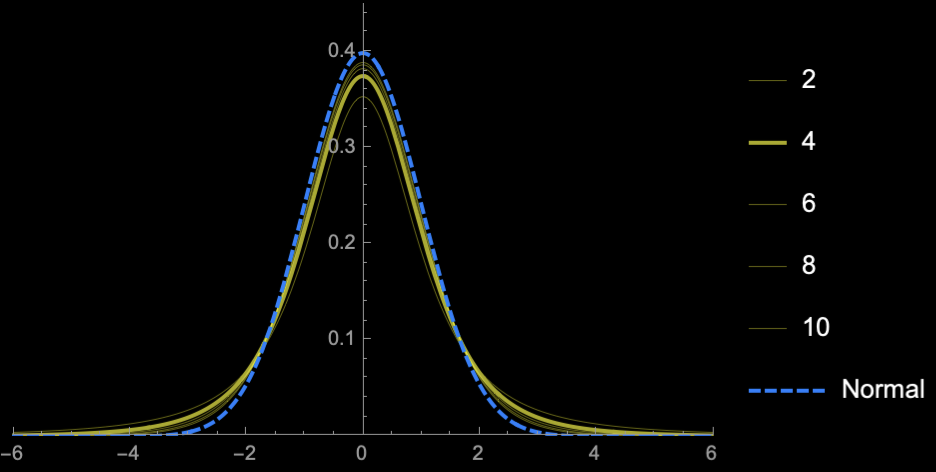
Student's T-distribution
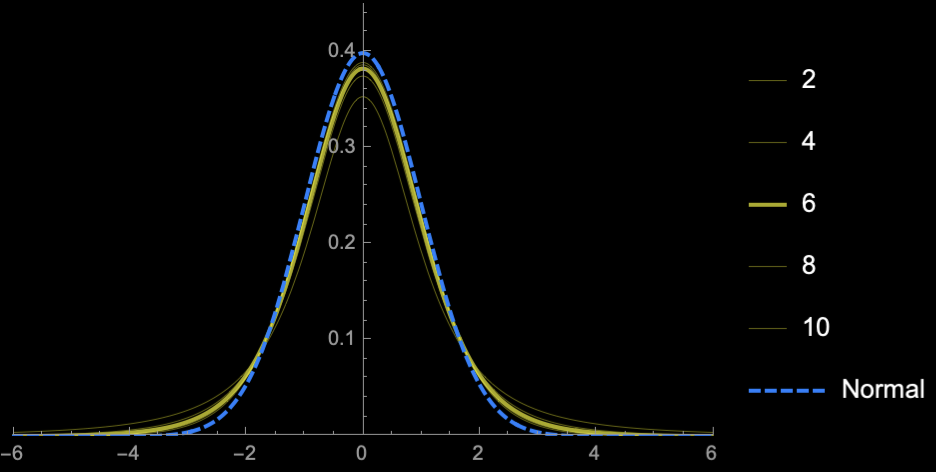
Student's T-distribution
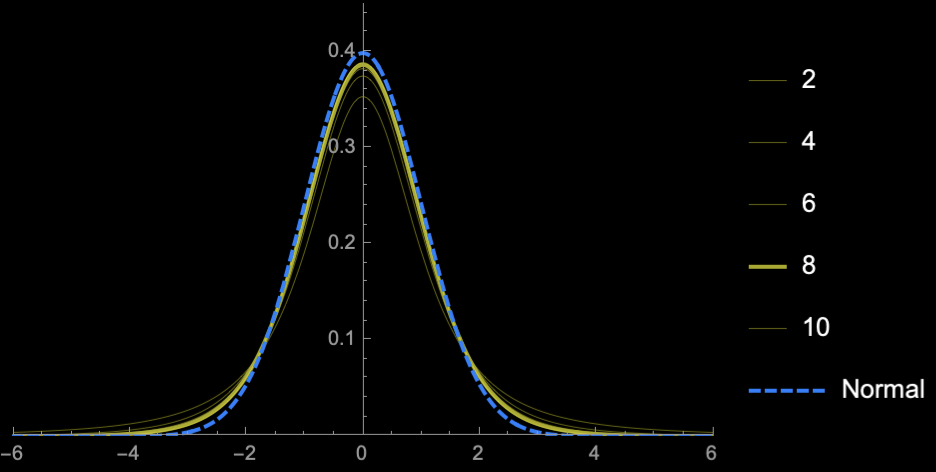
Student's T-distribution
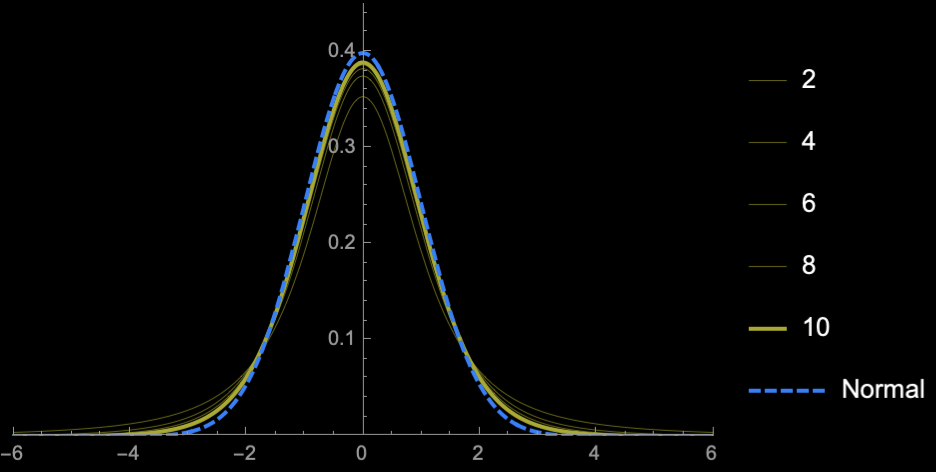
Student's T-distribution
Student's T-distribution
Student's T-distribution
Student's T-distribution
Interval Estimator of \(\mu\), unknown \(\sigma\)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) \approx (1 - \alpha)\)
For known \(\sigma\)
For unknown \(\sigma\)
\(\mathrm{Pr}(\overline{X} - t_{n-1, \alpha/2}\frac{S}{\sqrt{n}} < \mu < \overline{X} + t_{n - 1, \alpha/2}\frac{S}{\sqrt{n}}) = (1 - \alpha)\)
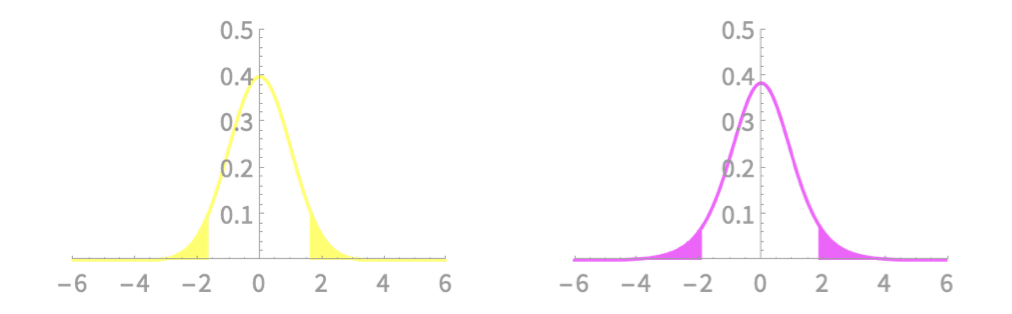
\(t_{n-1,\alpha/2}\)
Each of these areas is \(\alpha/2\)
\(-t_{n-1,\alpha/2}\)
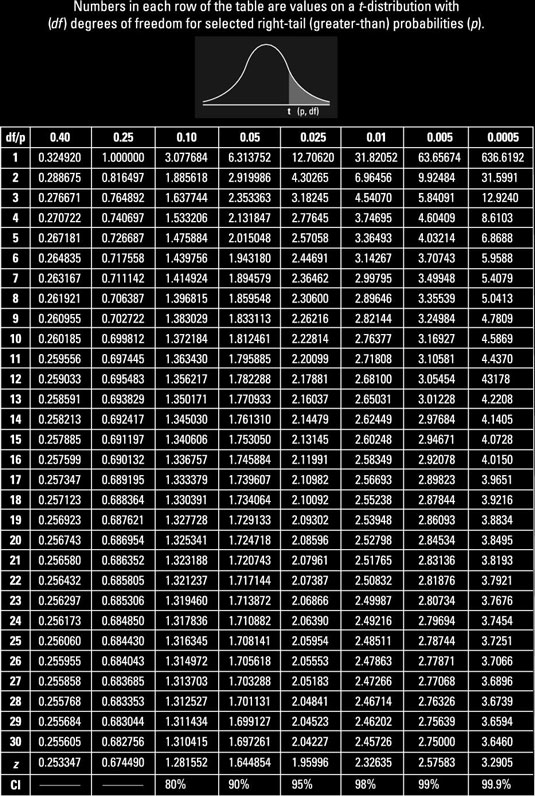


Comparing interval bounds with \(z\)- and \(t\)-variables
\(n = 7, p = 0.9\)
\(z\)-variable: \((-1.64, 1.64)\)
\(t\)-variable: \((-1.89, 1.89)\)

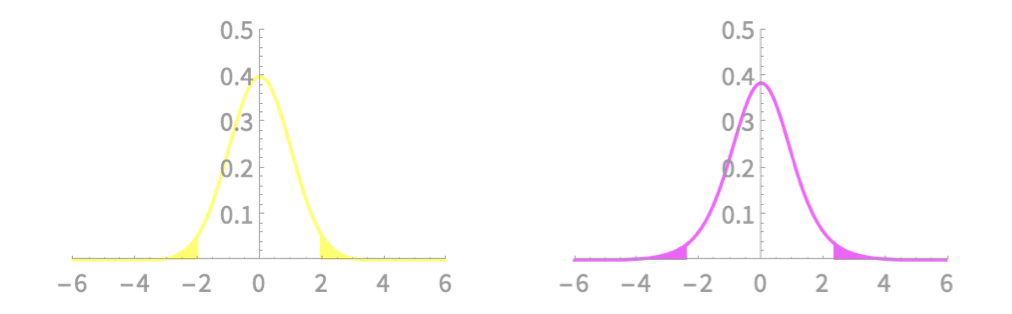
Comparing interval bounds with \(z\)- and \(t\)-variables
\(n = 7, p = 0.95\)
\(z\)-variable: \((-1.96, 1.96)\)
\(t\)-variable: \((-2.36, 2.36)\)
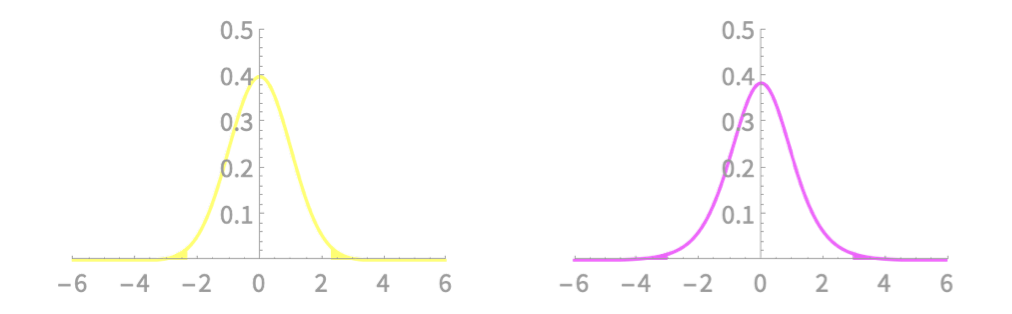
Comparing interval bounds with \(z\)- and \(t\)-variables
\(n = 7, p = 0.98\)
\(z\)-variable: \((-2.33,2.33)\)
\(t\)-variable: \((-2.99, 2.99)\)
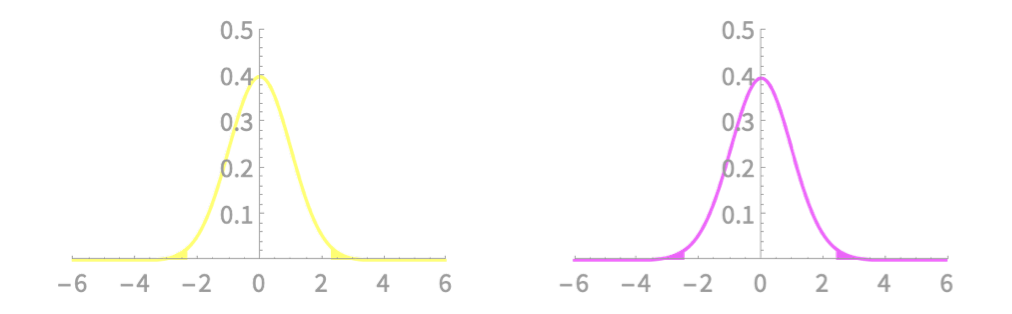
Comparing interval bounds with \(z\)- and \(t\)-variables
\(n = 30, p = 0.98\)
\(z\)-variable: \((-2.33,2.33)\)
\(t\)-variable: \((-2.46, 2.46)\)
Comparing interval bounds with \(z\)- and \(t\)-variables
Using \(t\)-variables leads to more inaccurate or wider confidence intervals
The difference to \(z\)-variables is particularly clearer for small sample sizes
In fact this is how the study of Student's \(t\)-distributions started: How do you perform estimation with small samples?

Willian Sealy
Computing interval bounds of \(\mu\) for unknown \(\sigma\)
You asked your 5 of your college wingies what their monthly salary was
Calculate the confidence interval for mean with probability 95%
68, 125, 130, 77, 83
Computing interval bounds of \(\mu\) for unknown \(\sigma\)
\(\alpha = 0.05\)
\(n = 5\)
\(S = 28.7\)
\(\overline{X} = 96.6\)
\(t_{n - 1, \alpha/2} = t_{4, 0.025} = 2.78 \)
\(\mathrm{Pr}(\overline{X} - t_{n-1, \alpha/2}\frac{S}{\sqrt{n}} < \mu < \overline{X} + t_{n - 1, \alpha/2}\frac{S}{\sqrt{n}}) = (1 - \alpha)\)
\(\mathrm{Pr}(96.6-35.7 < \mu < 96.6+35.7) = 0.95\)
\(\mu \in (60.9,132.3)\)
68, 125, 130, 77, 83
Computing interval bounds of \(\mu\) for known \(\sigma\)
\(\alpha = 0.05\)
\(n = 10\)
\(\sigma = 25\)
\(\overline{X} = 96.6\)
\(t_{5, 0.025} = 2.78 \)
\(z_{\alpha/2} = 1.96 \)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) = (1 - \alpha)\)
\(\mathrm{Pr}(96.6- 21.9 < \mu < 96.6+21.9) = (1 - \alpha)\)
\(\mu \in (74.7, 118.5 )\)
Stats secret:
I chose numbers with mean 100 and standard deviation 25
\(\mu \in (60.9,132.3)\)
Computing interval bounds of \(\mu\) for unknown \(\sigma\)
You are doing experiments and notice the errors in your measurements
Calculate the confidence interval for probability 95%
0.81, -0.51, -0.25, 0.50, -0.51, 0.03, -0.38, -0.74, -0.75, 0.16
Computing interval bounds of \(\mu\) for unknown \(\sigma\)
0.81, -0.51, -0.25, 0.50, -0.51, 0.03, -0.38, -0.74, -0.75, 0.16
\(\alpha = 0.05\)
\(n = 10\)
\(S = 0.53\)
\(\overline{X} = -0.16\)
\(t_{n - 1, \alpha/2} = t_{9, 0.025} = 2.26 \)
\(\mathrm{Pr}(\overline{X} - t_{n-1, \alpha/2}\frac{S}{\sqrt{n}} < \mu < \overline{X} + t_{n - 1, \alpha/2}\frac{S}{\sqrt{n}}) = (1 - \alpha)\)
\(\mathrm{Pr}(-0.16 - 0.38 < \mu < -0.16 + 0.38) = -.95\)
\(\mu \in (-0.54, 0.22)\)
Computing interval bounds of \(\mu\) for known \(\sigma\)
0.81, -0.51, -0.25, 0.50, -0.51, 0.03, -0.38, -0.74, -0.75, 0.16
\(\alpha = 0.05\)
\(n = 10\)
\(\sigma = 1\)
\(\overline{X} = -0.16\)
\(t_{9, 0.025} = 2.26 \)
\(\mu \in (-0.54, 0.22)\)
\(z_{\alpha/2} = 1.96 \)
\(\mathrm{Pr}(\overline{X} - z_{\alpha/2}\frac{\sigma}{\sqrt{n}} < \mu < \overline{X} + z_{\alpha/2}\frac{\sigma}{\sqrt{n}}) = (1 - \alpha)\)
\(\mathrm{Pr}(-0.16 - 0.62 < \mu < -0.16 +0.62) = (1 - \alpha)\)
\(\mu \in (-0.78, 0.46)\)
Stats secret:
I sampled from \(\mathcal{N}(0, 1)\)
Computing interval bounds for population proportion \(p\)
Recall that \(\mathbb{E}[\hat{p}] = p\) and \(\mathrm{sd}(\hat{p}) = \sqrt{\frac{p(1-p)}{n}}\)
So, we don't have two cases like with estimation of mean (known, unknown \(\sigma\))
Only option: assume \(n\) is large
Large enough such that \(\mathrm{sd}(\hat{p}) = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)
Recal rule thumb \(n\hat{p}, n(1-\hat{p}) > 10\)
Computing interval bounds for population proportion \(p\)
We have a large sample size \(n\)
\(\mathbb{E}[\hat{p}] = p\) and \(\mathrm{sd}(\hat{p}) = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)
Now to calculate interval bounds, we only need to invoke the likelihood computations with \(z\)-statistics
Computing interval bounds for population proportion \(p\)
\(\mathrm{Pr}\left(\hat{p} - z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} < p < \hat{p} + z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\right)= (1 - \alpha)\)
We have a large sample size \(n\)
\(\mathbb{E}[\hat{p}] = p\) and \(\mathrm{sd}(\hat{p}) = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\)
Computing interval bounds for population proportion \(p\)
"Do you program as a hobby?"
Responses by 64,416 developers
Source: StackOverflow
