Recap: List of Topics
Descriptive Statistics
Probability Theory
Inferential Statistics
Different types of data
Different types of plots
Measures of centrality and spread
Counting, Sample spaces, events
Discrete and continuous RVs
Bernoulli, Uniform, Normal dist.
Sampling strategies
Point and Interval Estimators
Hypothesis testing (z-test, t-test)
ANOVA, Chi-square test
Distribution of Sample Statistics
Recap: List of Topics
Descriptive Statistics
Probability Theory
Inferential Statistics
Different types of data
Different types of plots
Measures of centrality and spread
Counting, Sample spaces, events
Discrete and continuous RVs
Bernoulli, Uniform, Normal dist.
Sampling strategies
Point and Interval Estimators
Hypothesis testing (z-test, t-test)
ANOVA, Chi-square test
Distribution of Sample Statistics
Learning Objectives
Define what inferential statistics is
Contrast it to descriptive statistics
Recognize sampling as a random process
and sample statistics as random variables
Relate the distribution of sample statistics
to parameters of the population
Along the way:
Central Limit Theorem
Chi Square Distribution
Lets begin with a recap
Take a pause and recall the ideas of
population, sample, parameter, statistic
Basic Terms
A population is a collection of a large number of people, objects, or events under study

Examples
All people in India

Basic Terms
A population is a collection of a large number of people, objects, or events under study


Examples
All students writing the 10th board examinations in Bengaluru in 2021
Basic Terms
A population is a collection of a large number of people, objects, or events under study

Examples
All cars manufactured by Tesla
























Basic Terms
A population is a collection of a large number of people, objects, or events under study

Examples
Detections of particles in the Large Hadron Collider

























Basic Terms
A population is a collection of a large number of people, objects, or events under study

Examples
All possible hands in a game of cards

















These can also by collection of hypothetical items
Basic Terms
A population is a collection of a large number of people, objects, or events under study

Examples
All possible folds of a protein structure
These can also by collection of hypothetical items













Basic Terms
A parameter is a numeric property of the entire population

Examples
All people in India

Average per capita income
\(\mu_{income}\)
Basic Terms
A parameter is a numeric property of the entire population

Examples
Proportion of students passing the examination

All students writing the 10th board examinations in Bengaluru in 2020
\(p_{pass}\)
Basic Terms
A parameter is a numeric property of the entire population

Examples
Standard deviation of mileage across cars
All cars manufactured by Tesla
























\(\sigma_{mileage}\)
Basic Terms
A parameter is a numeric property of the entire population

Examples
Average time interval since previous detection
Detections of particles in the Large Hadron Collider

























\(\mu_{\tiny{\delta t}}\)
Basic Terms
A parameter is a numeric property of the entire population

Examples
Proportion of hands with a King of Diamonds
All possible hands in a game of cards

















\(p_{\tiny{K\Diamond}}\)
Basic Terms
A parameter is a numeric property of the entire population

Examples
All possible folds of a protein structure



















Average effectiveness of protein as a drug
\(\mu_{\tiny{effectiveness}}\)
Basic Terms
A parameter is a numeric property of the entire population

Calculate precisely
(probability theory)
Can measure, but may be expensive
Hard to measure, can estimate
How do we know the population parameters?
\(\sigma_{mileage}\)

























\(\mu_{income}\)
\(p_{\tiny{K\Diamond}}\)

















Basic Terms
A parameter is a numeric property of the entire population

How do we know the population parameters?
Population parameters are very useful
Hence, we create and study samples
But they are hard to compute
Very large population
Expensive data collection
Unknown
random process
Basic Terms
A sample is a subset chosen from a population using a defined procedure

Basic Terms
A sample is a subset chosen from a population using a defined procedure

Examples
All people in India




All people in India in a given age-group
0-5 yrs
5-10 yrs
> 100 yrs
Basic Terms
A sample is a subset chosen from a population using a defined procedure

Examples
All students writing the 10th board examinations in Bengaluru in 2021

All students in a given school



School 1
School 2
School n
Basic Terms
A sample is a subset chosen from a population using a defined procedure

Examples
All cars manufactured by Tesla
All cars manufactured in different factories
























Factory 1


















Factory 2
Factory k
Basic Terms
A sample is a subset chosen from a population using a defined procedure

Examples
All cars manufactured by Tesla
Random sample of 1% of cars manufactured
1%










































1%
1%
Basic Terms
A sample is a subset chosen from a population using a defined procedure

Examples

























Detections of particles in the Large Hadron Collider
All detections noted by a scientist

























Scientist 1
Scientist 2





















Scientist k
Basic Terms
A sample is a subset chosen from a population using a defined procedure

Examples
Hands obtained on doing n shuffles

















All possible hands in a game of cards















Shuffle set 1
Shuffle set 2
Shuffle set k
Basic Terms
A statistic is a numerical property of the entire sample

Examples




\(\overline{X_{income}}\)
All people in India
All people in India in a given age-group
Average per capita income
\(\overline{X_{income}}\)
\(\overline{X_{income}}\)
Basic Terms
A statistic is a numerical property of the entire sample

Examples
All students writing the 10th board examinations in Bengaluru in 2021




All students in a given school
Proportion of students passing the examination
\(\hat{p}_{pass}\)
\(\hat{p}_{pass}\)
\(\hat{p}_{pass}\)
Basic Terms
A statistic is a numerical property of the entire sample

Examples
Standard deviation of mileage across cars
\(S_{mileage}\)










































All cars manufactured by Tesla
Random sample of 1%
of cars manufactured
\(S_{mileage}\)
\(S_{mileage}\)
Basic Terms
A statistic is a numerical property of the entire sample

Examples
































\(\hat{p}_{\tiny{K\Diamond}}\)
\(\hat{p}_{\tiny{K\Diamond}}\)
\(\hat{p}_{\tiny{K\Diamond}}\)
Hands obtained on doing n random shuffles
All possible hands in a game of cards
Proportion of hands with a King of Diamonds
Why do we compute statistics
1. To describe the sample
Why do we compute statistics
1. To describe the sample
Examples
All students writing the 10th board examinations in Bengaluru in 2021




An education officer
visiting the school can
get a quick summary of
performance with \(\hat{p}_{pass}\)
\(\hat{p}_{pass}\)
\(\hat{p}_{pass}\)
\(\hat{p}_{pass}\)
\(\Rightarrow\) may be used to identify schools requiring aid
Why do we compute statistics
1. To describe the sample
Examples
Elon Musk can find out which factory is doing better
\(\Rightarrow\) may be used to
identify the best manufacturing settings
\(S_{mileage}\)










































All cars manufactured by Tesla
\(S_{mileage}\)
\(S_{mileage}\)
Why do we compute statistics
1. To describe the sample
Examples
Student can check computed proportion against theoretical estimate
\(\Rightarrow\) to evaluate student's learning or play Poker
All possible hands in a game of cards
































\(\hat{p}_{\tiny{K\Diamond}}\)
\(\hat{p}_{\tiny{K\Diamond}}\)
\(\hat{p}_{\tiny{K\Diamond}}\)
Legitimate use-cases 😃
Why do we compute statistics
1. To describe the sample
Examples
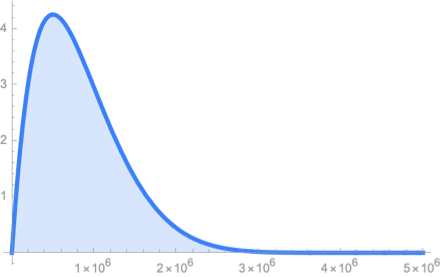
Apart from just single statistic, we can
visualise distributions
compute statistics for sub-sets of sample
Plotting a violin plot of the distribution of income of all people in India

Computing the standard deviation of mileage across the 4 Telsa models
Why do we compute statistics
2. To estimate population parameters
1. To describe the sample
3. To test hypotheses
Inferential statistics
Descriptive statistics
Why do we compute statistics
2. To estimate population parameters
1. To describe the sample
3. To test hypotheses
Estimate Population Parameters
Let's understand this with examples
Given
sample statistics
estimate
population parameter
Estimate Population Parameters




\(\overline{X_{income}}\)
\(\overline{X_{income}}\)
\(\overline{X_{income}}\)
\(\mu_{income}\)
Given
sample statistics
estimate
population parameter
Examples
Estimate Population Parameters
Given
sample statistics
estimate
population parameter
\(S_{mileage}\)










































\(S_{mileage}\)
\(S_{mileage}\)
\(\sigma_{mileage}\)
Examples
Estimate Population Parameters
Given
sample statistics
estimate
population parameter
































\(\hat{p}_{\tiny{K\Diamond}}\)
\(\hat{p}_{\tiny{K\Diamond}}\)
\(\hat{p}_{\tiny{K\Diamond}}\)
\(p_{\tiny{K\Diamond}}\)
Examples
Estimate Population Parameters
Given
sample statistics
estimate
population parameter
We are not interested in estimation methods that work for a particular dataset
We are looking for mathematical relations that hold true generally
This generality requires us to make
two key assumptions
Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution

Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution



Rs 75K

Rs 1.5L

Rs 30L

Rs 50K

Rs 80K

Rs 6L
Income \(\rightarrow\)
Rs 75K
Rs 30L
Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution



Rs 75K

Rs 1.5L

Rs 30L

Rs 50K

Rs 80K

Rs 6L
The assumption is not about smoothness or shape of this curve
It is that such a curve exists and is common for all
Income \(\rightarrow\)
Rs 75K
Rs 30L

Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution


Rs 75K

Rs 1.5L

Rs 30L

Rs 50K

Rs 80K

Rs 6L
If we choose each element's value in sequence, then
1. they are independent
2. they follow the same distribution
Income \(\rightarrow\)
Rs 75K
Rs 30L

Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution



















False

True

False

False

True

False
True
False
\(p_{\tiny{K\Diamond}}\)
If each set had 13 cards, then \(Pr(True) = 0.25\), \(Pr(False) = 0.75\)
We know this holds for each element, independently
Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution



















False

True

False

False

True

False
True
False
\(p_{\tiny{K\Diamond}}\)
In this case, we know the distribution
In general, we don't know it and only assume that it exists
Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution

Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

This assumption constrains the method which we use to generate the random samples
Let us understand by checking if earlier examples satisfy this assumption
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample





0-5 yrs
5-10 yrs
> 100 yrs
A person who is 105 years old cannot be present in these samples
He can only be present in this
sample
Violates assumption
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample





0-5 yrs
5-10 yrs
> 100 yrs
We cannot use this sampling method when doing inferential statistics
We are free to use it for descriptive statistics
Violates assumption
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

Similar reasoning
Student of one school can only be present in the respective school's sample
Violates assumption




School 1
School 2
School n
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

Similar reasoning
Violates assumption
























Factory 1


















Factory 2
Factory k
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

Similar reasoning
Violates assumption


















































Scientist 1
Scientist 2





















Scientist k
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

Each sample is a random selection of 1% of all cars
1%










































1%
1%
Any car in the population is equally likely to be in any sample
Meets assumption
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

Each sample is obtained from independent random shuffles
Meets assumption
































Shuffle set 1
Shuffle set 2
Shuffle set k
Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

With the examples, we have developed an intuition for the assumption
Let us formalise it by defining a
probability space
But before that a quick recap
Recap: Probability
A probability space is given by the triple (\(\Omega, F, P)\) where \(\Omega\) is the set of possible outcomes, \(F\) is the set of events, and \(P\) maps events to a probability

A random variable is a measurable function that maps outcomes in a probability space to real numbers

Recap: Probability
\(\Omega\)
Outcomes
\(F\)
0
1
Probability \(\rightarrow\)
\(F\)
\(P\)
2
4
5
\(X\)
2
4
5
\(Pr(X)\)
Recap: Probability
Consider a fair "three-faced" die
We throw it two times to generate elements of the probability space
\(\Omega\)
⚀⚁
⚀⚀
⚁⚁
⚁⚂
⚂⚂
⚁⚁
⚀⚂
\(F\)
\(F\)
⚀⚀
⚀⚁
⚁⚁
⚀⚂
⚁⚂
⚂⚂
\(P\)
0
1
\(\dfrac{1}{9}\)
\(\dfrac{2}{9}\)
⚀⚀
⚀⚁
⚁⚁
⚀⚂
⚁⚂
⚂⚂
2
4
5
\(X\)
6
3
2
4
5
\(Pr(X)\)
3
6
Example
We ignore the order
Back to Assumption 2
Each element of the population has an equal chance of being selected in any sample

Let us now formalise assumption of random sampling using a probability space
Formalism of Assumption 2
Think of samples as the outcomes of a probability space
Because each element of population should be equally likely to occur in each sample, we have:
1. All samples are of same size
3. Probability of each sample is equal
Each element of the population has an equal chance of being selected in any sample

2. All possible samples are outcomes
Formalism of Assumption 2

\(\Omega\)
\(F\)
Population size = \(N\)
Size of each sample = \(n\)
1. All samples are of same size










Formalism of Assumption 2

\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
Number of samples = \(|\Omega| =\)\( N \choose n\)










\(F\)
2. All samples are considered outcomes
Formalism of Assumption 2

\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
Number of samples = \(|\Omega| =\)\( N \choose n\)










\(F\)
3. Probability of each sample is equal

0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)





Formalism of Assumption 2

\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)










\(F\)

0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)






0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)





\(X\)






What kinds of random variables are we interested in?
Formalism of Assumption 2

\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)










\(F\)

0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)






0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)





\(X\)






Since we have samples, we can use statistics

Aha! moment
Formalism of Assumption 2

\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)










\(F\)

0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)






0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)





\(X\)






Use sample mean as the random variable
\(\overline{X_{income}}\)

Rs 1.5L

Rs 3L

Rs 70K
Formalism of Assumption 2

\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)










\(F\)

0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)






0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)





\(X\)






\(\overline{X_{income}}\)

Rs 1.5L

Rs 3L

Rs 70K
We can plot probability distribution of random var.
Formalism of Assumption 2

\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)










\(F\)

0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)






0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)





\(X\)






\(\overline{X_{income}}\)

Rs 1.5L

Rs 3L

Rs 70K
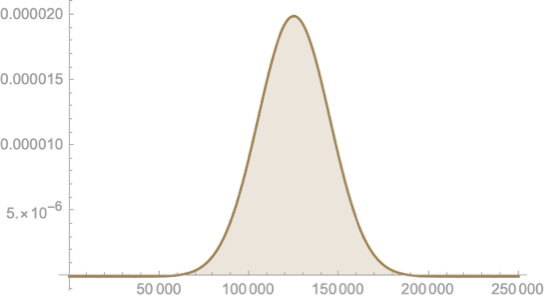
\(Pr(\overline{X})\)
Formalism of Assumption 2
\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)
\(F\)
0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)
























0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)








































































\(X\)




































We are looking at variation across cars
Random variable set as standard deviation
Formalism of Assumption 2
\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)
\(F\)
0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)
























0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)








































































\(X\)




































We are looking at variation across cars
Random variable set as standard deviation

10 km

30 km

5 km
\(S_{\tiny{mileage}}\)
Formalism of Assumption 2
\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)
\(F\)
0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)
























0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)








































































\(X\)





































10 km

40 km

5 km
\(S_{\tiny{mileage}}\)
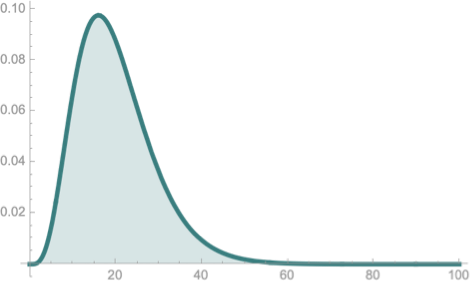
\(Pr(S_{mileage})\)
Formalism of Assumption 2
\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)
\(F\)
0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)
0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)
\(X\)































































































































We are calculating fraction of shuffles with King of Diamonds
Formalism of Assumption 2
\(\Omega\)
Population size = \(N\)
Size of each sample = \(n\)
\(|\Omega| =\)\( N \choose n\)
\(F\)
0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)
0
1
\(P\)
\(\dfrac{1}{|\Omega|}\)
\(X\)































































































































\(Pr(\hat{p}_{\tiny{K\Diamond}})\)

1/4

1

0

2/4

3/4
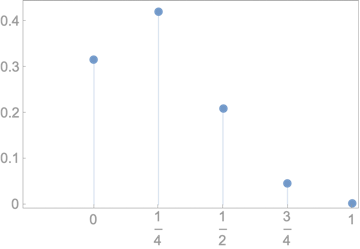
\(\hat{p}_{\tiny{K\Diamond}}\)
Formalism of Assumption 2
\(Pr(\hat{p}_{\tiny{K\Diamond}})\)


\(Pr(S_{mileage})\)

\(Pr(\overline{X})\)
In each case we chose a sample statistic as a random variable
We have seen three examples of sampling
And we are interested in the probability distribution of these variables
Hence, the title: Distribution of sample statistics
Recall the two assumptions of sampling
Assumption 1: Population
The values of interest of the elements in the population are independent random variables with a common distribution

Assumption 2: Random Sample
Each element of the population has an equal chance of being selected in any sample

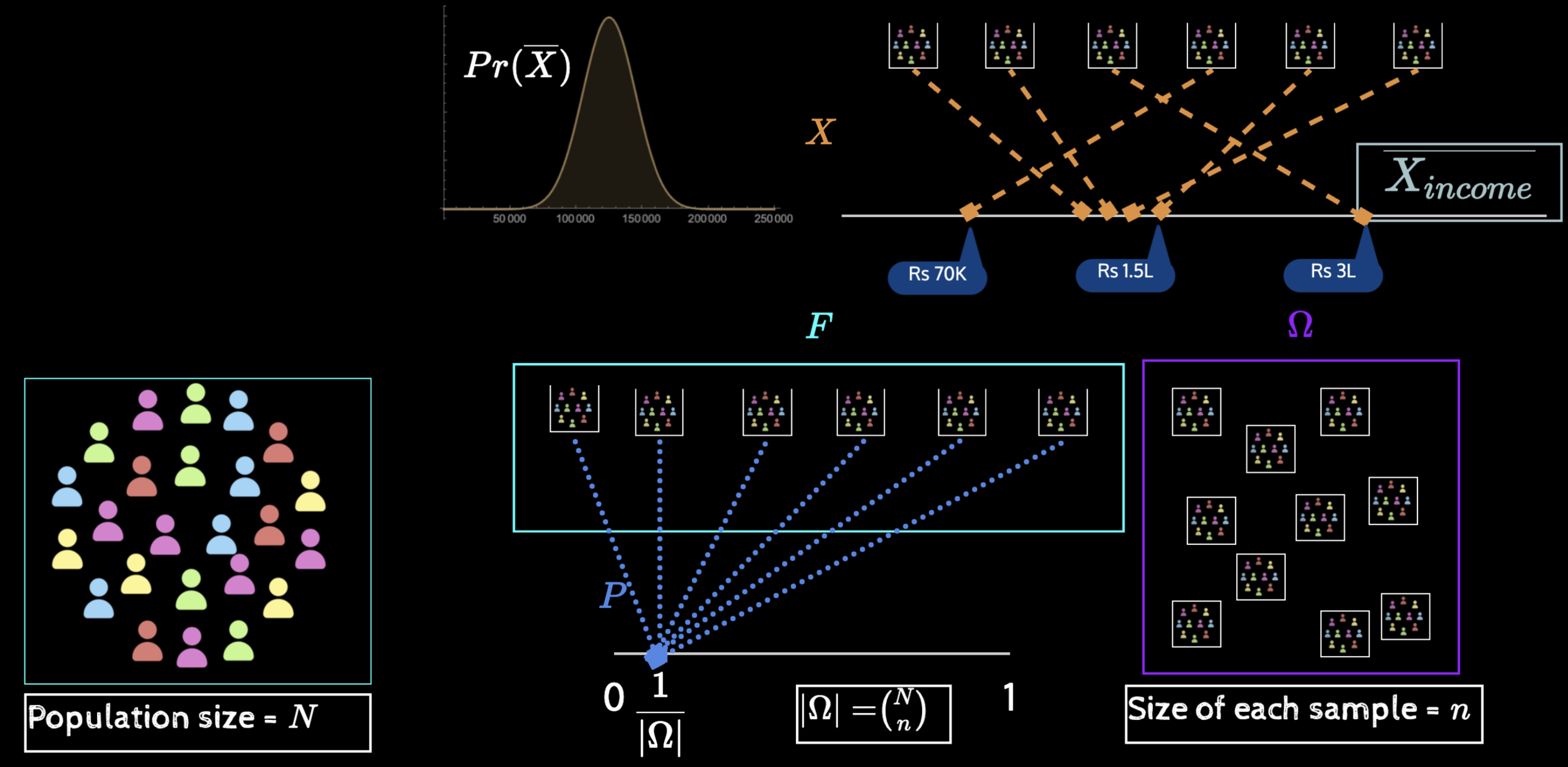
What is inferential statistics?
\(\mu_{income}, \sigma_{income}\)


Given distribution of sample statistics
Find population parameters
This is a hard problem
We will do the reverse

What is inferential statistics?
\(\mu_{income}, \sigma_{income}\)


Given population parameters
Find distribution of sample statistics
Once we build insight, we will take up the original problem
Our Roadmap


