Learning Valve Task using Reinforcement Learning
Okan YILDIRAN
DARPA Robotics Challenge
The DARPA Robotics Challenge (DRC) seeks to address this problem by promoting innovation in human-supervised robotic technology for disaster-response operations.


Tasks

Valve Task
Valve task for robots is still a difficult problem for robotics field. In DARPA Robotics Challenge, there are sections that required to fully turn various valves in order to get points.

Simulator
- V-rep
- ROS
- IIS-Lab
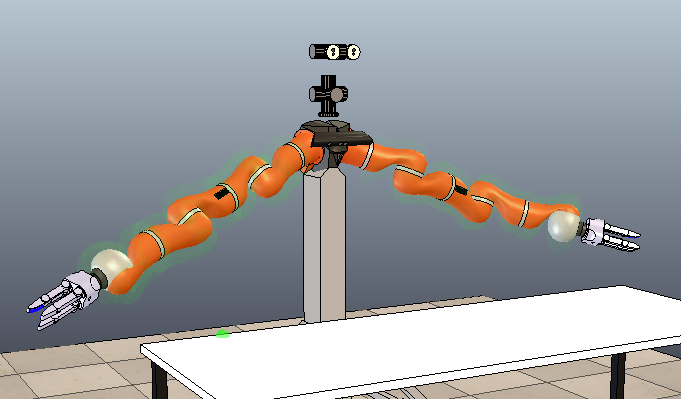

My simulator
- V-rep
- ROS
- YouBot from CMPE565
- Without wheels!
- 1000 kg weight
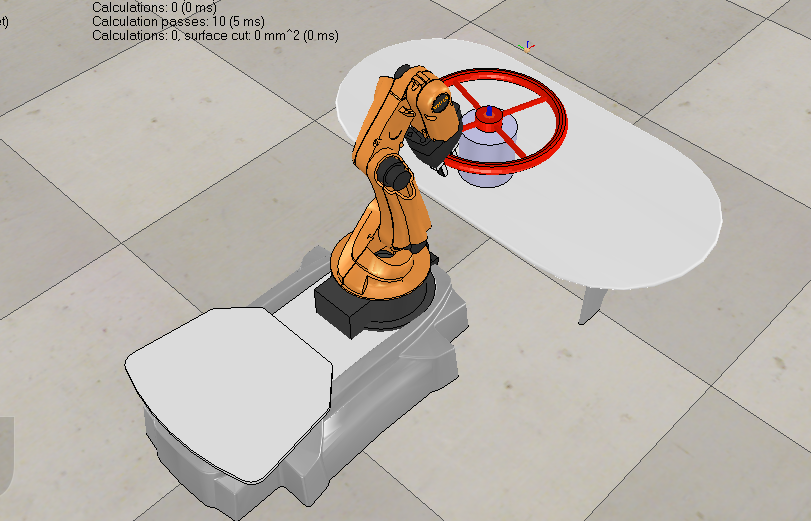
In this project, experimented with similar scenario to DARPA, using reinforcement learning algorithm Sarsa, on ROS and VREP simulation environment.
Introduction
State-Action-Reward-State-Action (SARSA) is an algorithm for learning a Markov decision process policy, used in the reinforcement learning. It is an on-policy version of Temporal Difference (TD) algorithm.
Sarsa

Temporal Difference algorithms need lots of episodes in order to find good policy. To reduce required episodes, Eligibility Traces used widely. Eligibility traces are one of the basic mechanisms of reinforcement learning and they increase the efficiency dramatically. Combining it with SARSA, which is called Sarsa(λ).
Sarsa(λ)

In experiments xy-plane on top of the valve discretizated in order to reduce state space. States are x and y positions of the end effector of the robot arm.
States
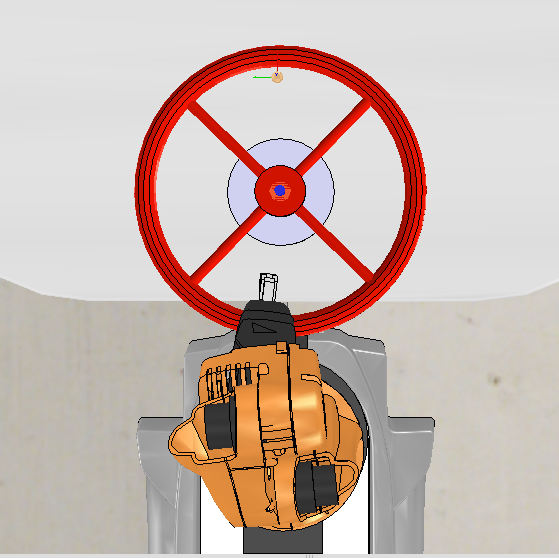
Actions are defined as 8-directional movements.
In some states, it is not possible to move to another state while gripping. For example while gripping, moving towards to center of the valve is not possible.
Due to the limitations of the robot's arm and existence of impossible actions, we can say that actions are non-deterministic.
Actions


Current Location
For valve task, reward function can be the angle of rotation or single reward at fully rotation. However due to not being able to fully implement physics of a valve in VREP simulation environment, rewards is defined at couple of locations in the state space.
Reward Function

Goals
Some movements are not possible. These movements are given small amount of negative reward in order to find possible actions.
Reward Function

Goals
Learning rate = 0.1
E-greedy = 0.9 to 0 over time
Discount factor = 0.9
λ = 0.9
Episodes = 50
Max step for episode = 50
Non-change limit = 5
Parameters

Goals