Atomic physics
The quantum description of atoms
Atomic physics
The quantum description of atoms
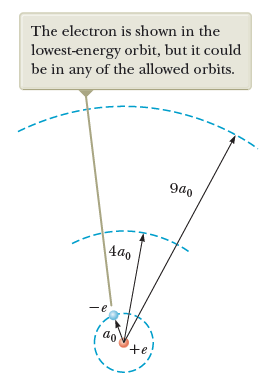
Recall: Bohr's Model of the Hydrogen Atom
Atomic models
Bohr's model
Quantization of electronic orbits
Atomic Physics
Introduction
Recall: Bohr's Model of the Hydrogen Atom
Atomic physics
The quantum description of atoms
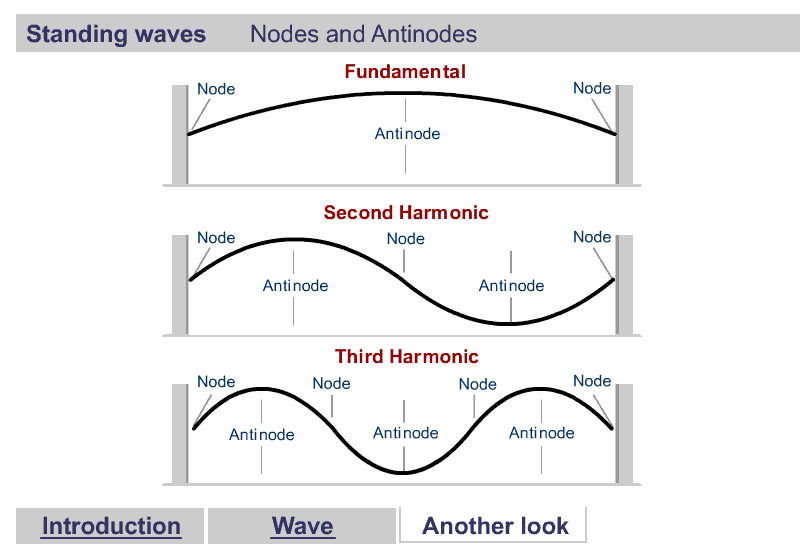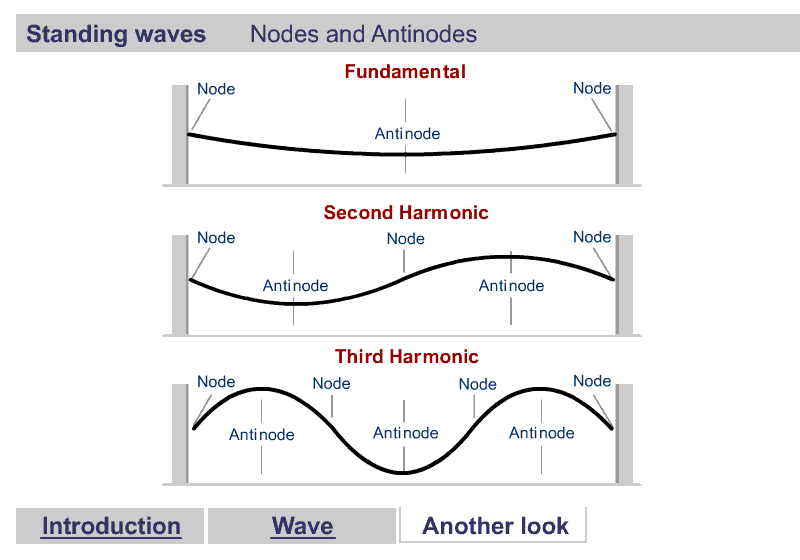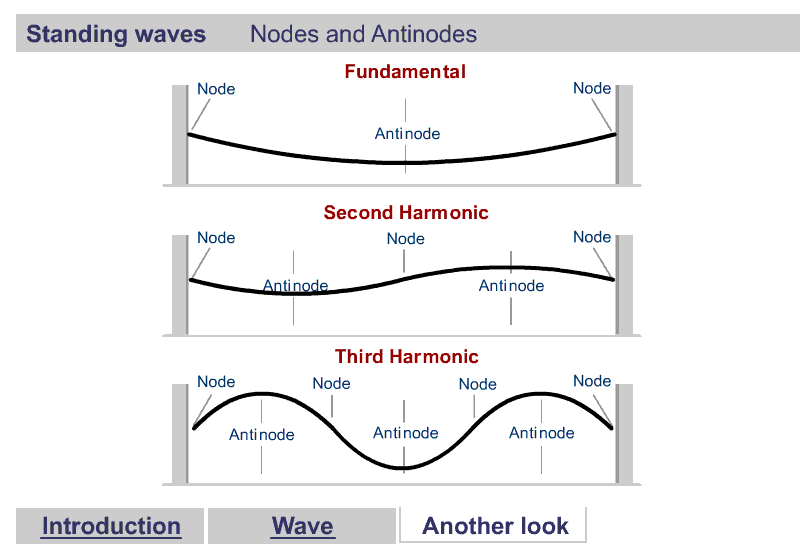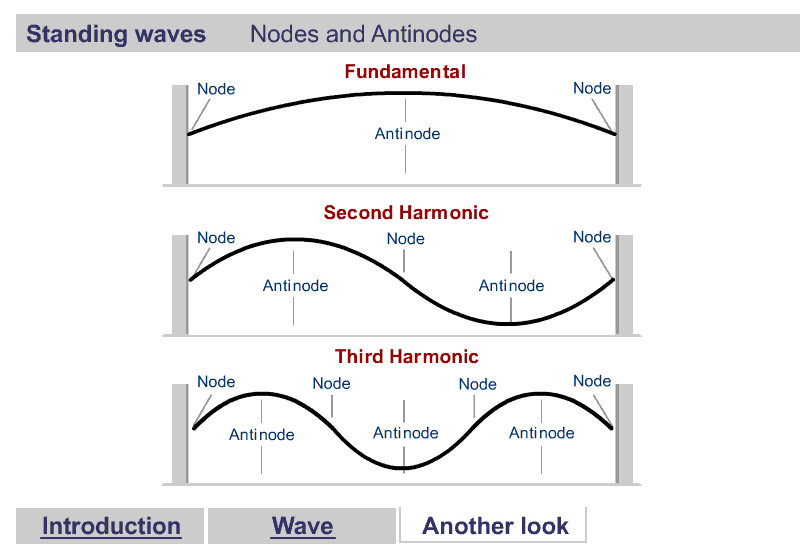
A quick word about Harmonics
Atomic Physics
Harmonics
What are Harmonics?
Waves are correlated amplitudes across space and time.


Atomic Physics
Harmonics
One Dimensional Harmonics
Classical: Standing waves on a string
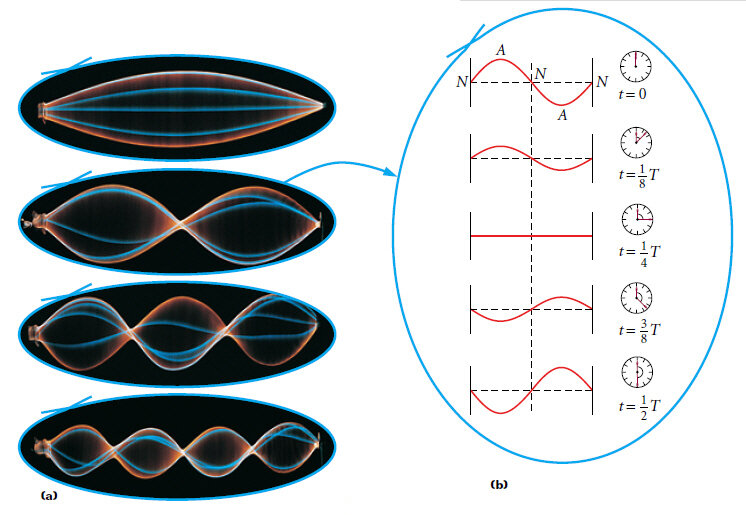
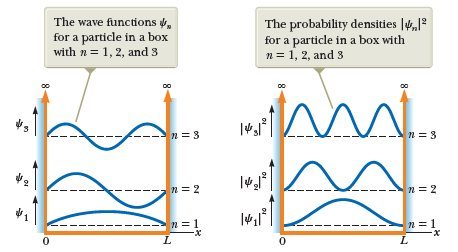
Quantum: infinite well
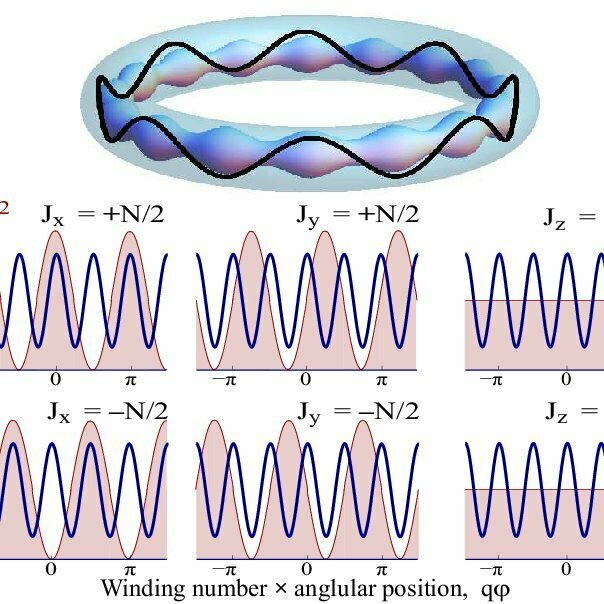
1D ring in 2D
Atomic Physics
Harmonics
One Dimensional Harmonics: time dependence
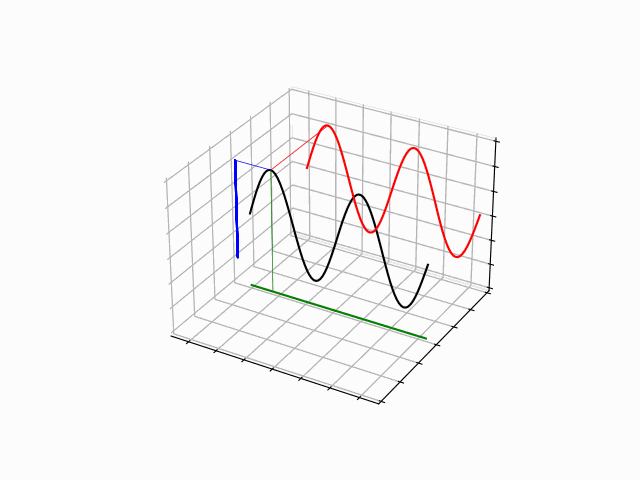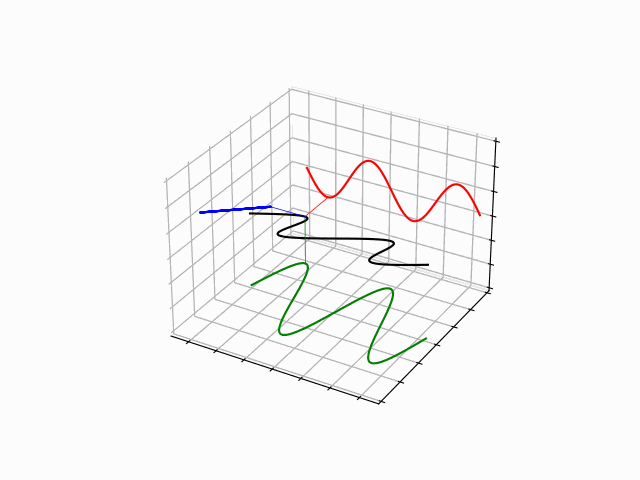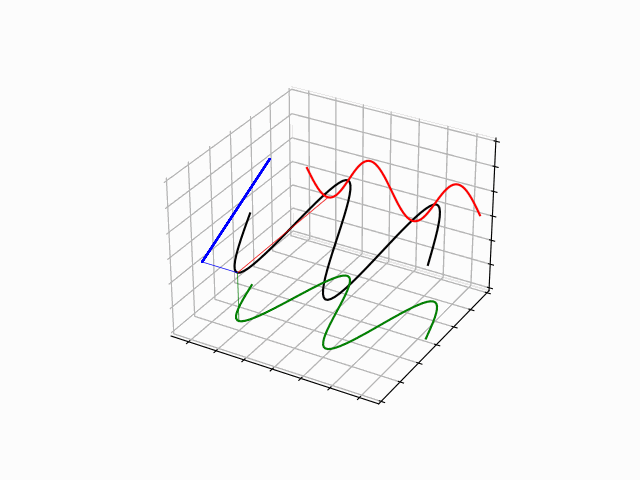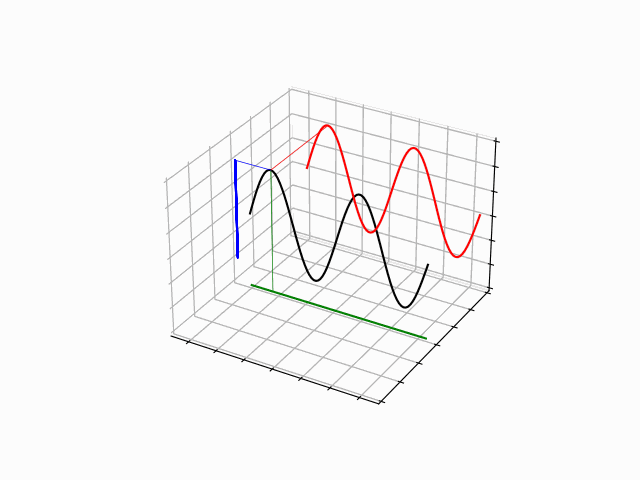
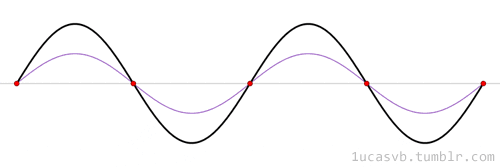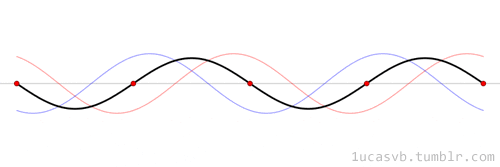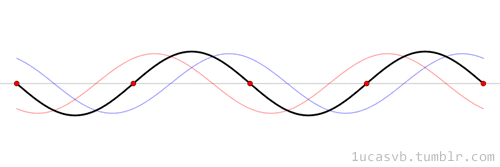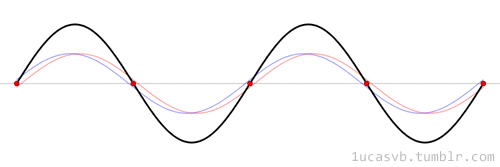
The time evolution can be understood as an interference between oppositely traveling waves (with opposite but equal momenta)
The number of nodes and antinodes depends on the momentum
The time evolution of quantum states is in the form of a time dependent phase.
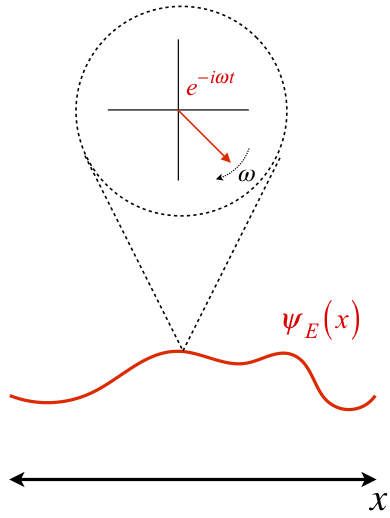
Atomic Physics
Harmonics
Two Dimensional Harmonics
2D-harmonics
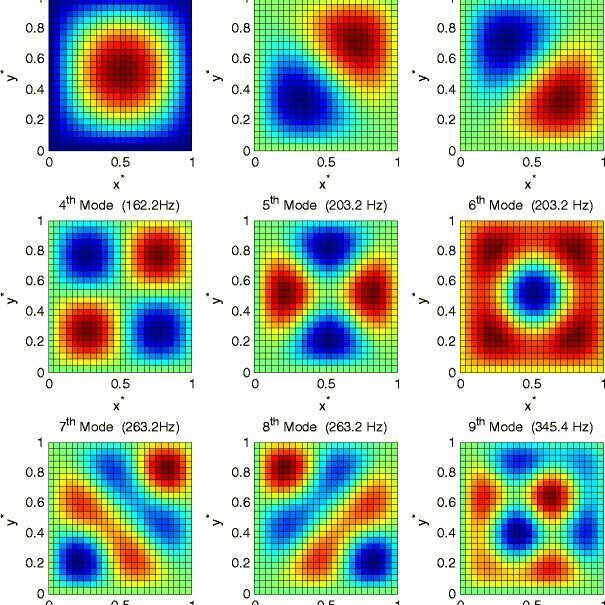

Cymatics
Atomic Physics
Harmonics
Two Dimensional Harmonics
2D-harmonics

Cymatics
Quantum infinite well
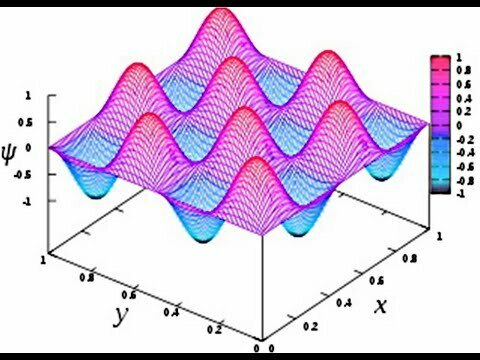
Atomic Physics
Harmonics
Two Dimensional Harmonics
2D-harmonics

2D surface in 3D
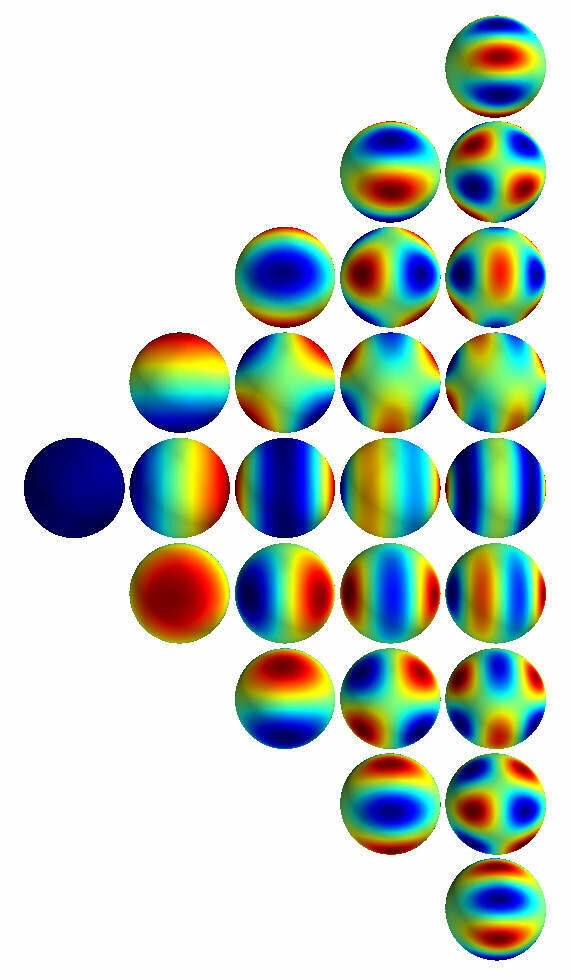
spherical Harmonics
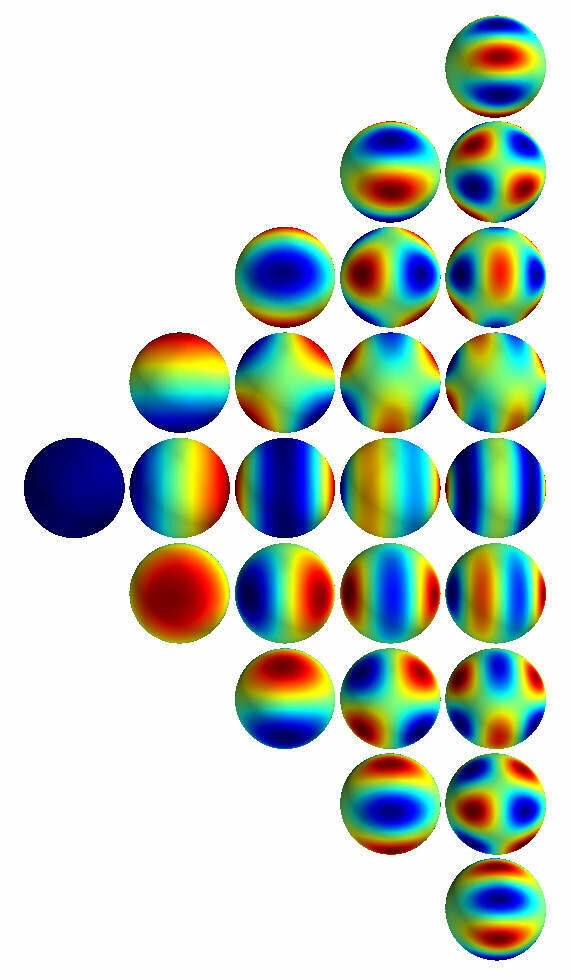
Atomic physics
The quantum description of atoms
Schrodinger's Wave Equation in 3D - Cartesian Coodinates
Atomic Physics
Introduction
Schrodinger's wave equation in 3-D
Recall the time-independent Schrodinger wave equation in one dimension
generalizing to 3-dimensions, this equation takes the form:
Atomic Physics
Introduction
3-D infinite box
Consider a 3-D box, where the potential vanishes inside, but is infinite outside, containing an otherwise free particle.
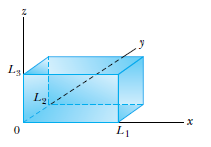
It is reasonable to assume a solution of the form
Satisfying the boundary conditions
Which is a solution to Schrodinger's equation, with energies
Atomic Physics
Introduction
3-D infinite box
If all the lengths are equal, cubic potential, then

Ground state is unique (nondegenerate)
First excited state is degenerate, with degeneracy = 3
Atomic Physics
Introduction
The Schrodinger Wave Equation in spherical coordinates
The Schrodinger wave equation in spherical coordinates:
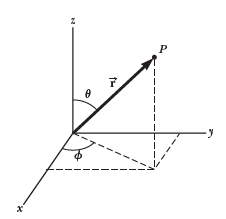

Atomic physics
The quantum description of atoms
Schrodinger's Wave Equation in 3D - Spherical Coordinates
Atomic Physics
The Hydrogen Atom
The Schrodinger Wave Equation in spherical coordinates
To a good approximation the potential energy of the electron-proton system in the hydrogen atom is spherically symmetric:
... to the time-independent Schrodinger wave equation:
So we can assume a separable solution
Atomic Physics
The Hydrogen Atom
The Schrodinger Wave Equation in spherical coordinates
... to the time-independent Schrodinger wave equation:
which, after many efforts by many people and quite a bit of math, leads to the solution:



Atomic Physics
The Hydrogen Atom
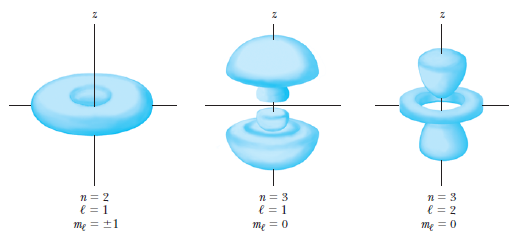
Quantum Numbers
Principal quantum number
Orbital angular momentum quantum number
Magnetic quantum number
Atomic Physics
The Hydrogen Atom
Quantum Numbers
Enumerate the quantum numbers for states with and count the degeneracy of each set.
Atomic Physics
The Hydrogen Atom
Probability density
The probability of finding the particle in an infinitesimal volume element
is given by:
which, when integrated over
gives a radial probability density of
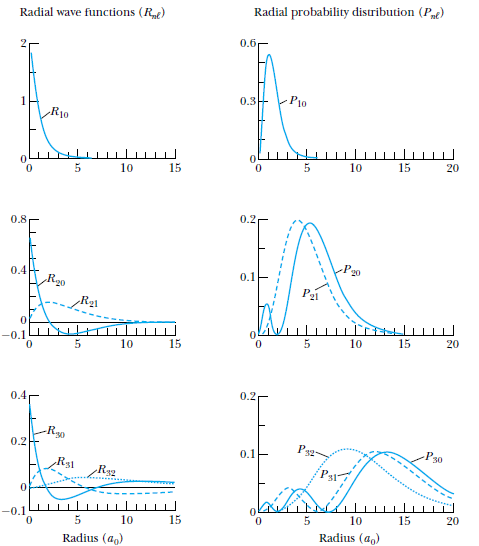
Atomic Physics
The Hydrogen Atom
Probability density


Atomic Physics
The Hydrogen Atom
Probability density
Atomic physics
The quantum description of atoms
Other Atoms
Atomic Physics
Other atoms
Shells, subshells, and the periodic table
Adding more protons and electrons to atoms is mathematically challenging.
Accurate results are obtained numerically.
Atomic Physics
Other atoms
Shells, subshells, and the periodic table
Two more important pieces to building atoms
Spin quantum number
Pauli's exclusion principle
No two electrons can have exactly the same set of quantum numbers
Atomic Physics
Other atoms
Shells, subshells, and the periodic table
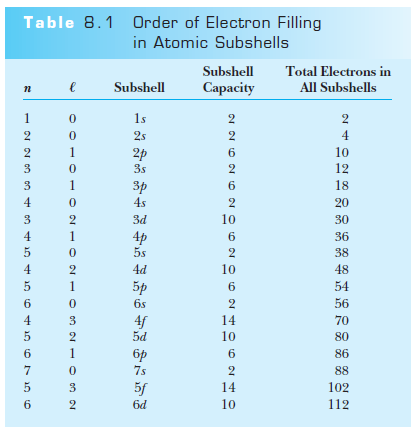
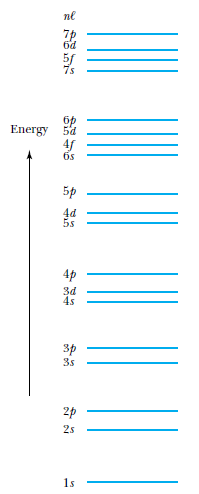
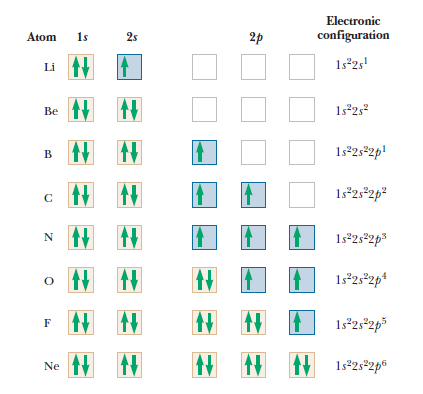
Atomic Physics
Other atoms
Shells, subshells, and the periodic table

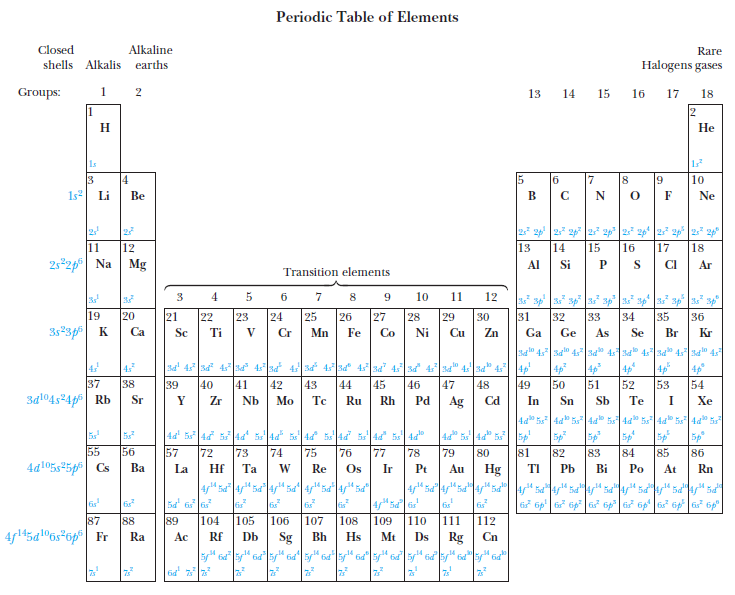
Atomic Physics
Other atoms
Shells, subshells, and the periodic table

Atomic Physics
Other atoms
Other forms of the periodic ...