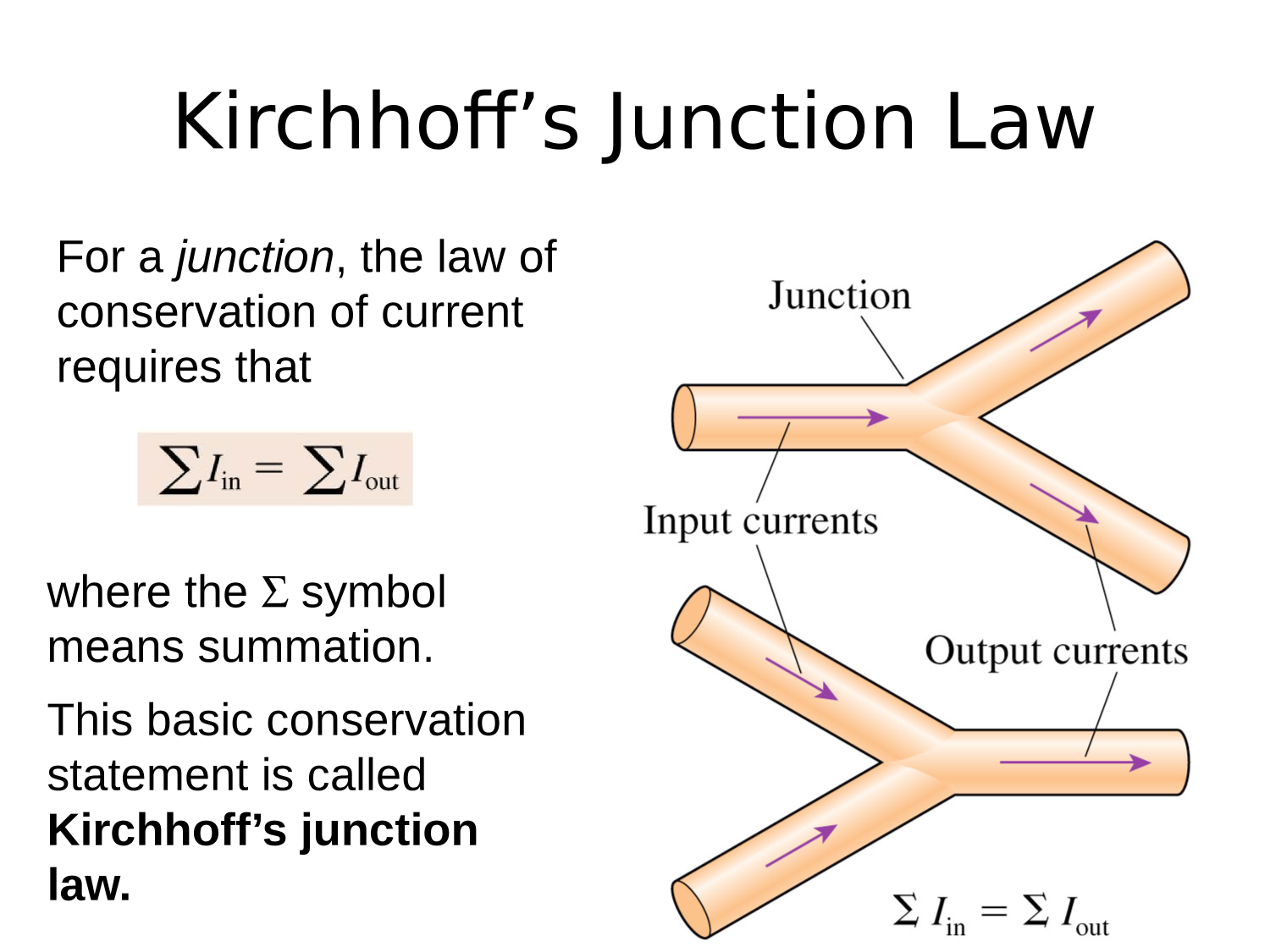
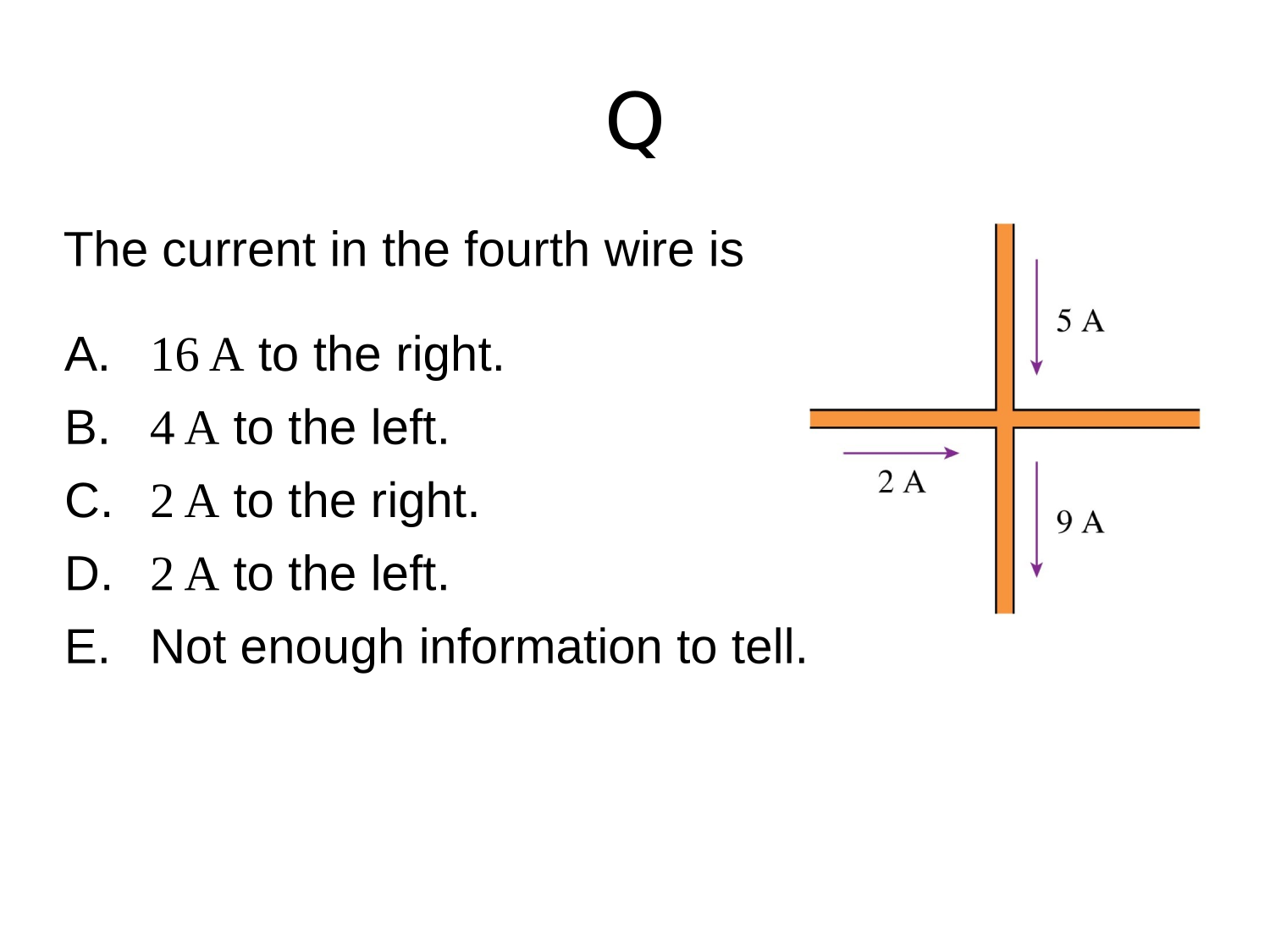
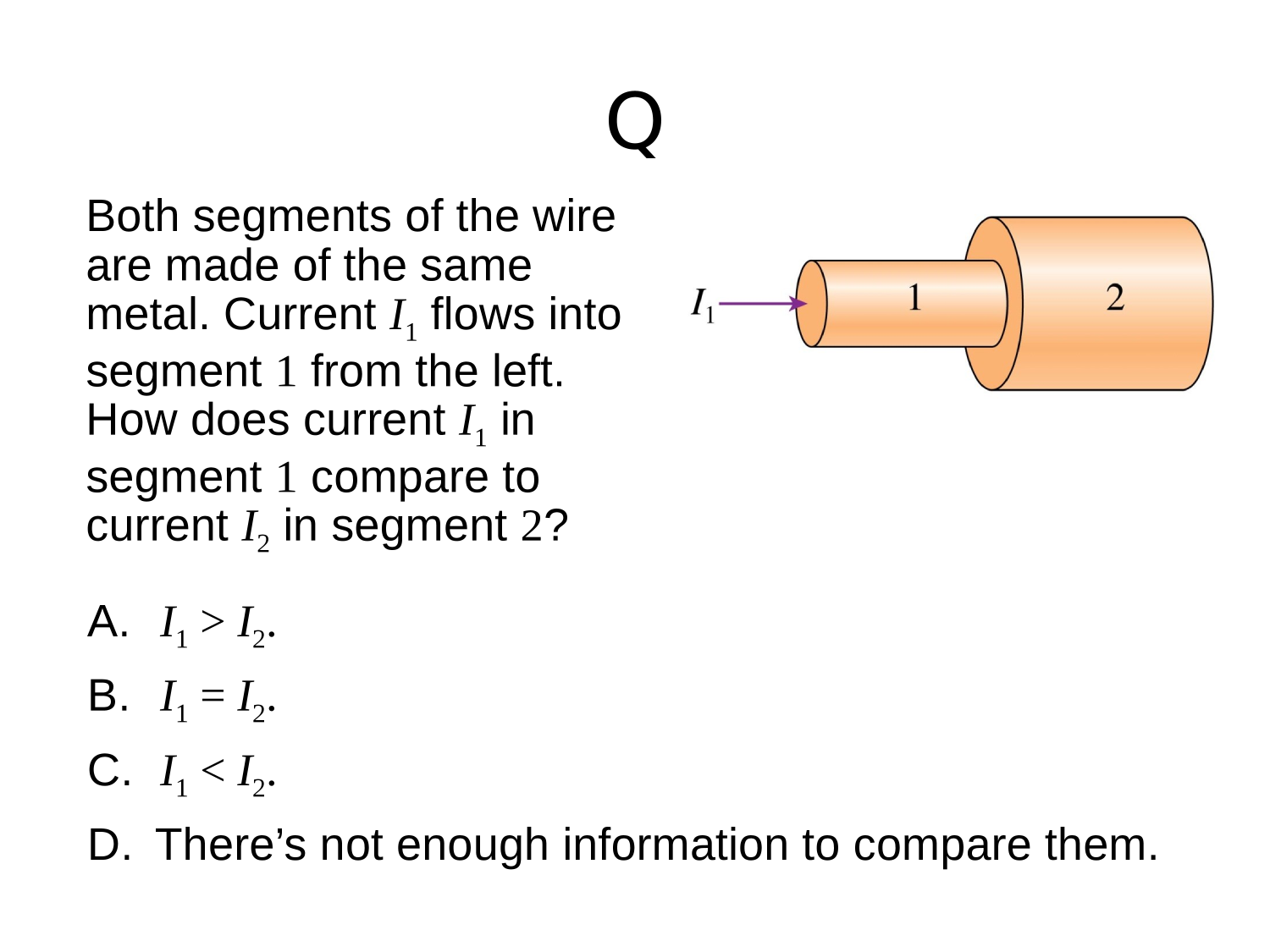
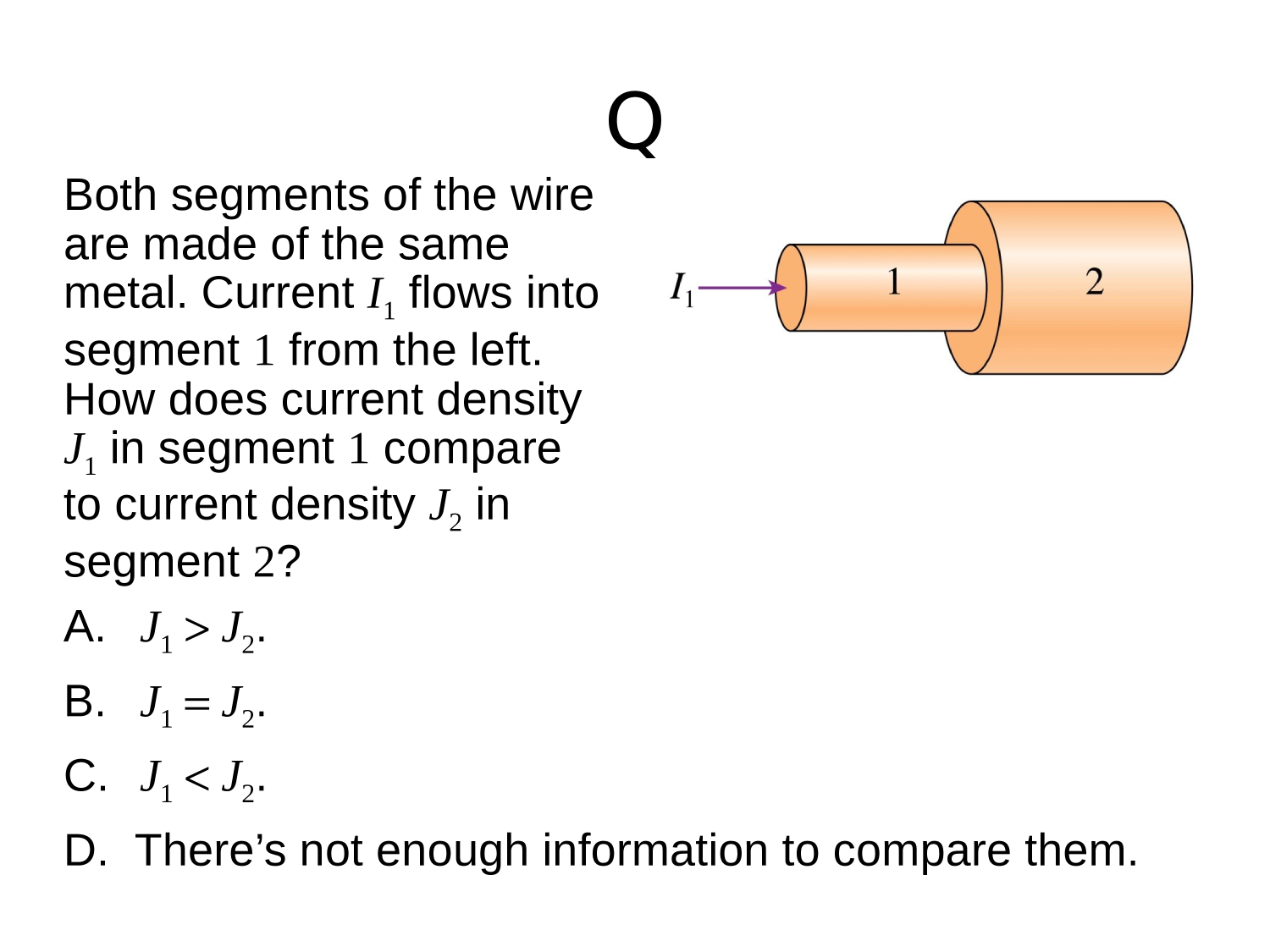
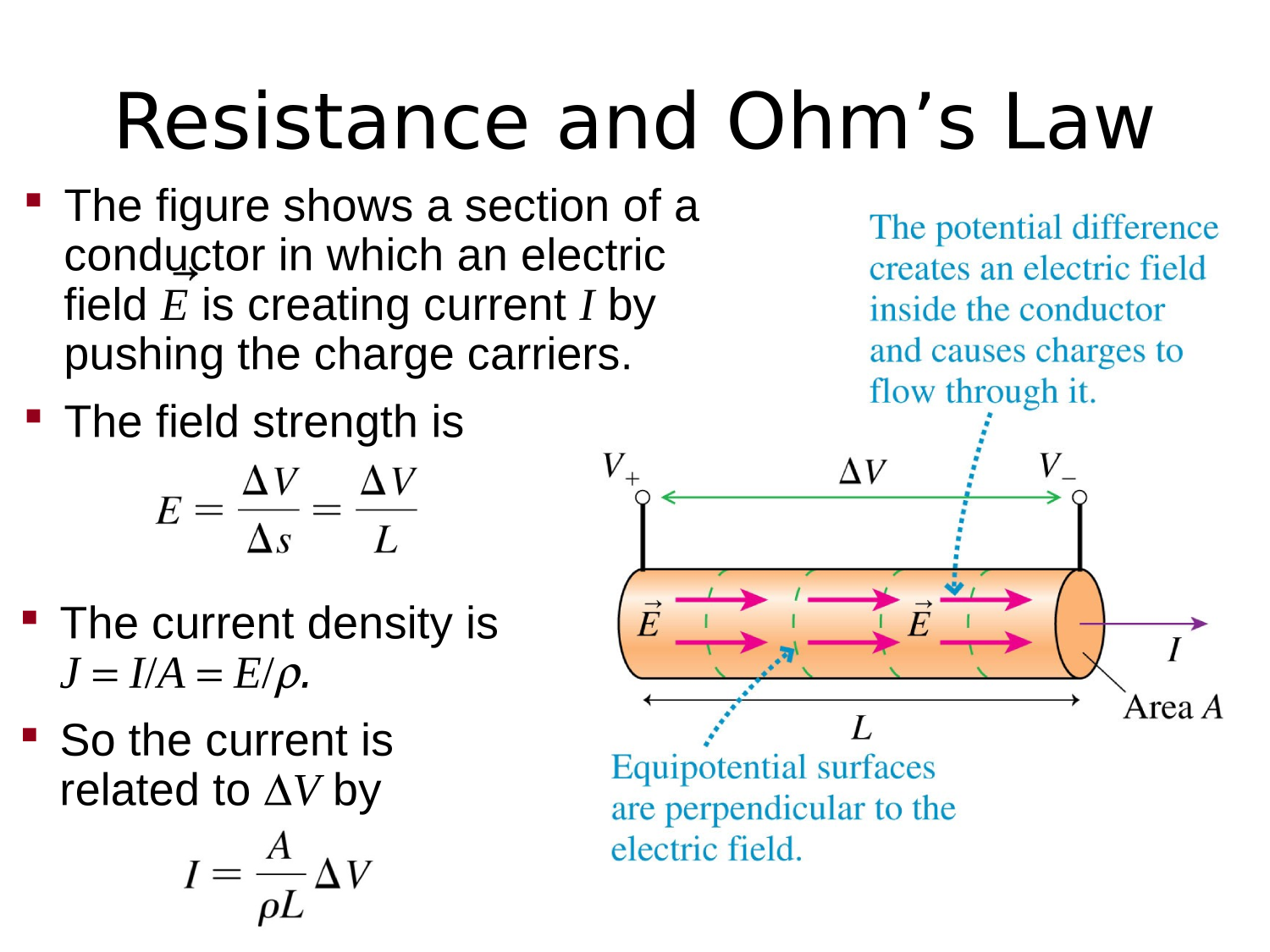
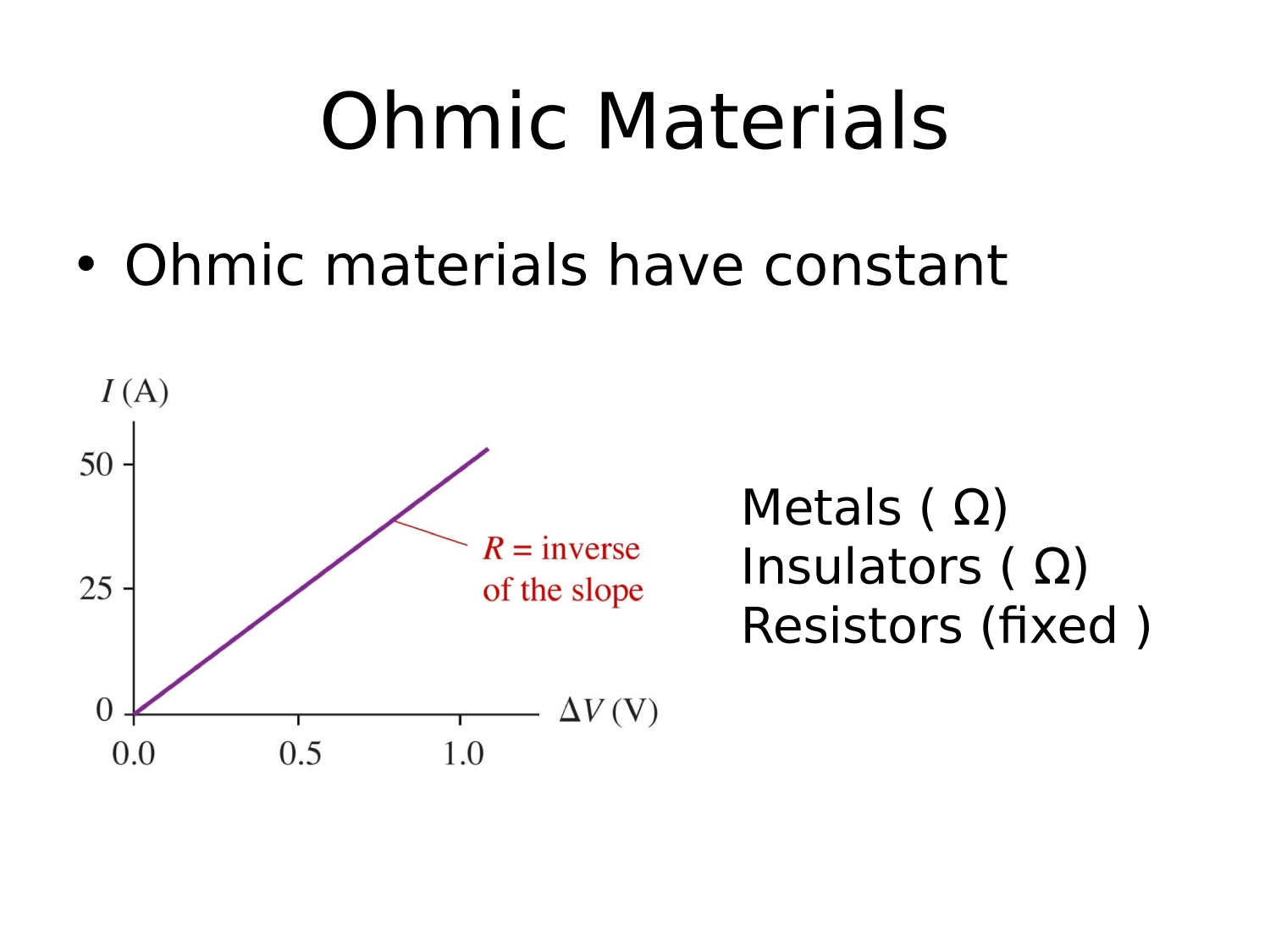
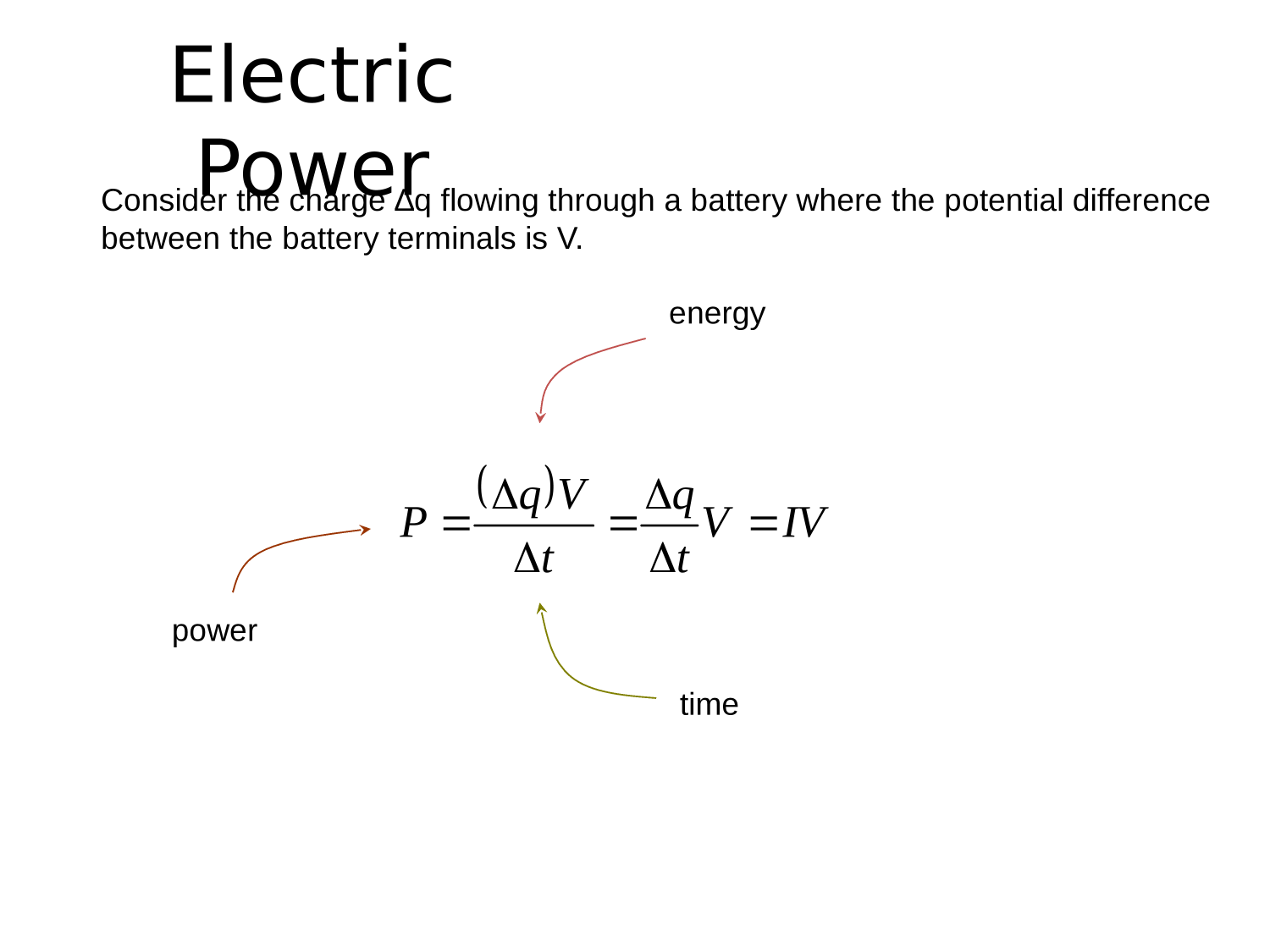
Electric Circuits
There are three important physical quantities to keep track of in an electric circuit
Electric Potential
Electric Current
Resistance (Impedance)



First, you need a conductor

as a conduit for electricity
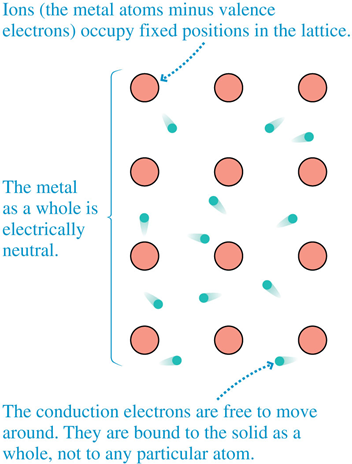

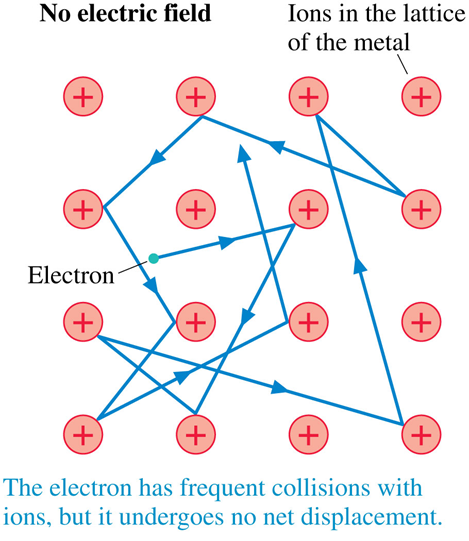
The "conduction" electrons bounce around.


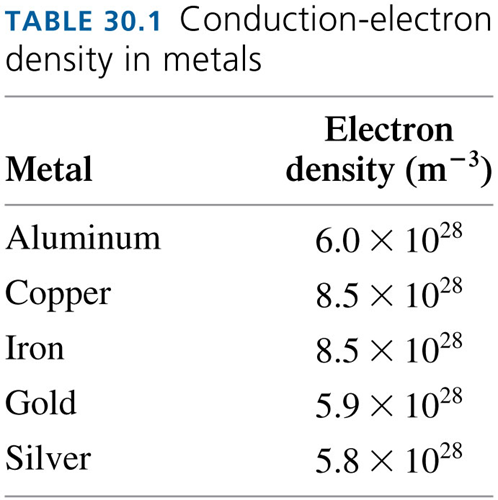
Q: What is the average speed of an electron within the metal?
A: Assuming a simple model of a 3D electron gas @ room temp:
\frac{1}{2}m_e v^2=\frac{3}{2}k_B T
v=\sqrt{\frac{3k_B T}{m_e}}\approx 10^5 \: m/s
\text{Kinetic Energy} = \text{Thermal Energy}
Electric field inside a conductor?!?

Suppose we setup an electric field inside the conductor...
Yes,charges are moving -- this is not electrostatic equilibrium!
How do you setup an electric field inside the conductor?
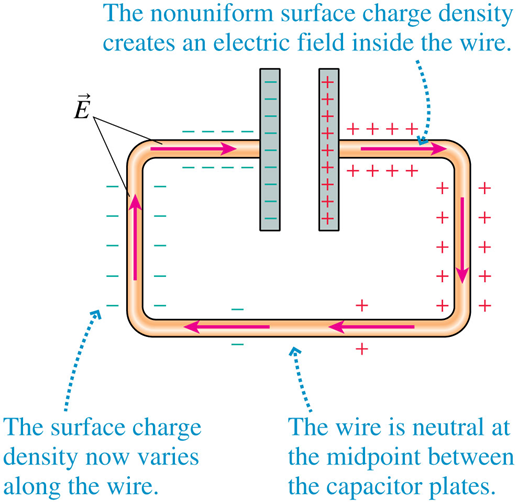
e.g. Discharging a capacitor
modeled here by tilting the board
So we setup an electric field inside the conductor
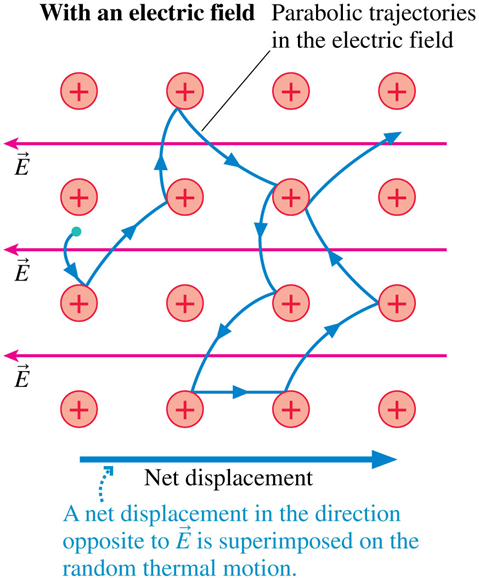
Q: Why are the trajectories parabolic?
A: Projectile motion
\implies \vec{a} = \frac{q_e}{m_e} \vec{E}
\implies q_e \vec{E} = m_e \vec{a}
\Delta\vec{r} = \vec{v}_0 t + \tfrac{1}{2}\vec{a}t^2
Constant acceleration in direction opposite of field,
and constant velocity perpendicular to field.
\vec{F} = m \vec{a}
So we setup an electric field inside the conductor

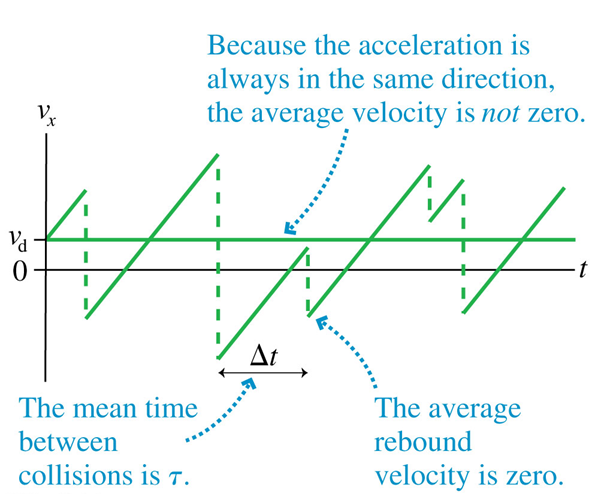
Q: What is the average "drift" velocity?
A: very slow ~
~ 10^{-4} m/s
{v}_{d} = a\ t
v_d = \frac{q_e \tau}{m_e} E
If the average time between collisions is
\tau
then
Then, you make a wire


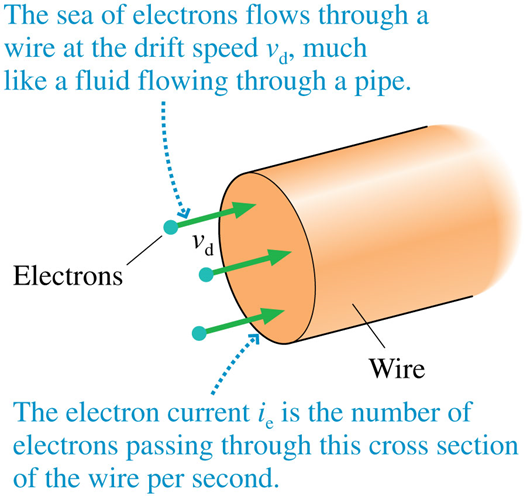
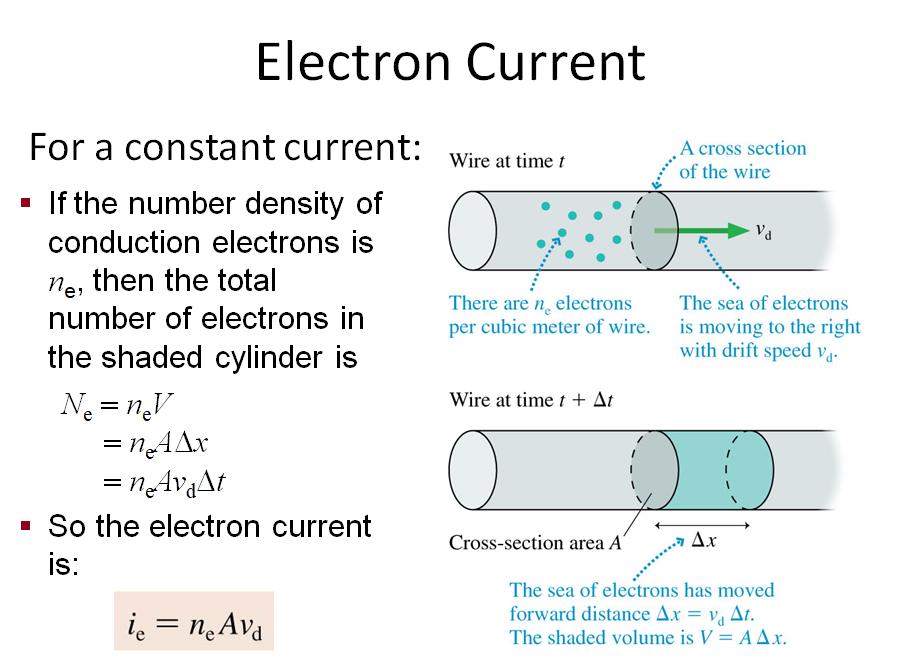
\implies i_e= \frac{n_e\ A\ q_e\ \tau}{m_e} E
Conventional Current
The rate of charge flow in a conductor

I = \frac{dQ}{dt}
The SI unit for conventional current is the Ampere
A = \frac{C}{s}
Conventional Current
I = \frac{\Delta Q}{\Delta t} = \frac{q_e N_e}{\Delta t} = q_e\ i_e
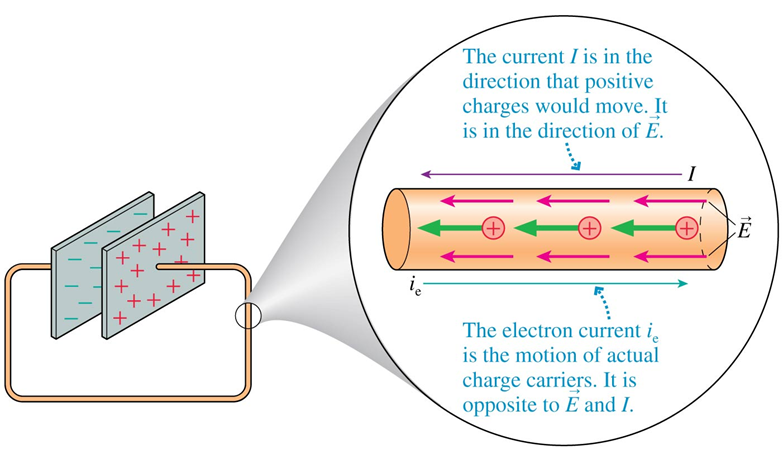
Electron Current
vs