Magnetism

Charged Particles
- influence is described in terms of
The influence
and interactions
of
Story so far was about
Electric
Fields

3-D Electric Field Caused by two identical Point Charges
- interaction is described in terms of
Electric
Forces
Charged Particles
The influence
and interactions
of
Today's story...
moving

3-D Electric Field Caused by two identical Point Charges
Biot-Savart Law
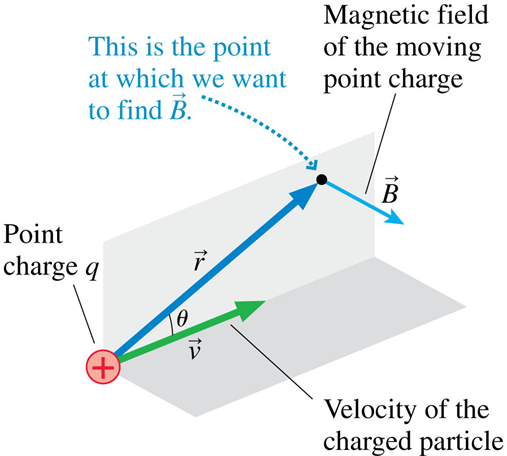
\vec{B}=\frac{\mu_0}{4\pi}\frac{q\ \vec{v}\ \times \ \hat{r}}{r^2}

Direction is given by
Right-Hand-Rule
Magnitude is given by
{B}=\frac{\mu_0}{4\pi}\frac{q\ v\ \text{sin}\theta }{r^2}
\mu_0=4\pi\times 10^{-7} T\ m/A
[B]=\text{T for Tesla}
Biot-Savart Law
\vec{B}=\frac{\mu_0}{4\pi}\frac{q\ \vec{v}\ \times \ \hat{r}}{r^2}

Direction is given by
Right-Hand-Rule
Magnitude is given by
{B}=\frac{\mu_0}{4\pi}\frac{q\ v\ \text{sin}\theta }{r^2}
\mu_0=4\pi\times 10^{-7} T\ m/A
[B]=\text{T for Tesla}

Biot-Savart Law
\vec{B}=\frac{\mu_0}{4\pi}\frac{q\ \vec{v}\ \times \ \hat{r}}{r^2}
•Sources are moving charges
–If velocity is zero, magnetic field is zero!
–
•Superposition principle applies
–Just like electric fields, magnetic field vectors add linearly!
–
•Biot-Savart Law
–Magnetic field strength has inverse square dependence on the distance from the moving charge
Important Highlights
Biot-Savart Law
\vec{B}=\frac{\mu_0}{4\pi}\frac{q\ \vec{v}\ \times \ \hat{r}}{r^2}

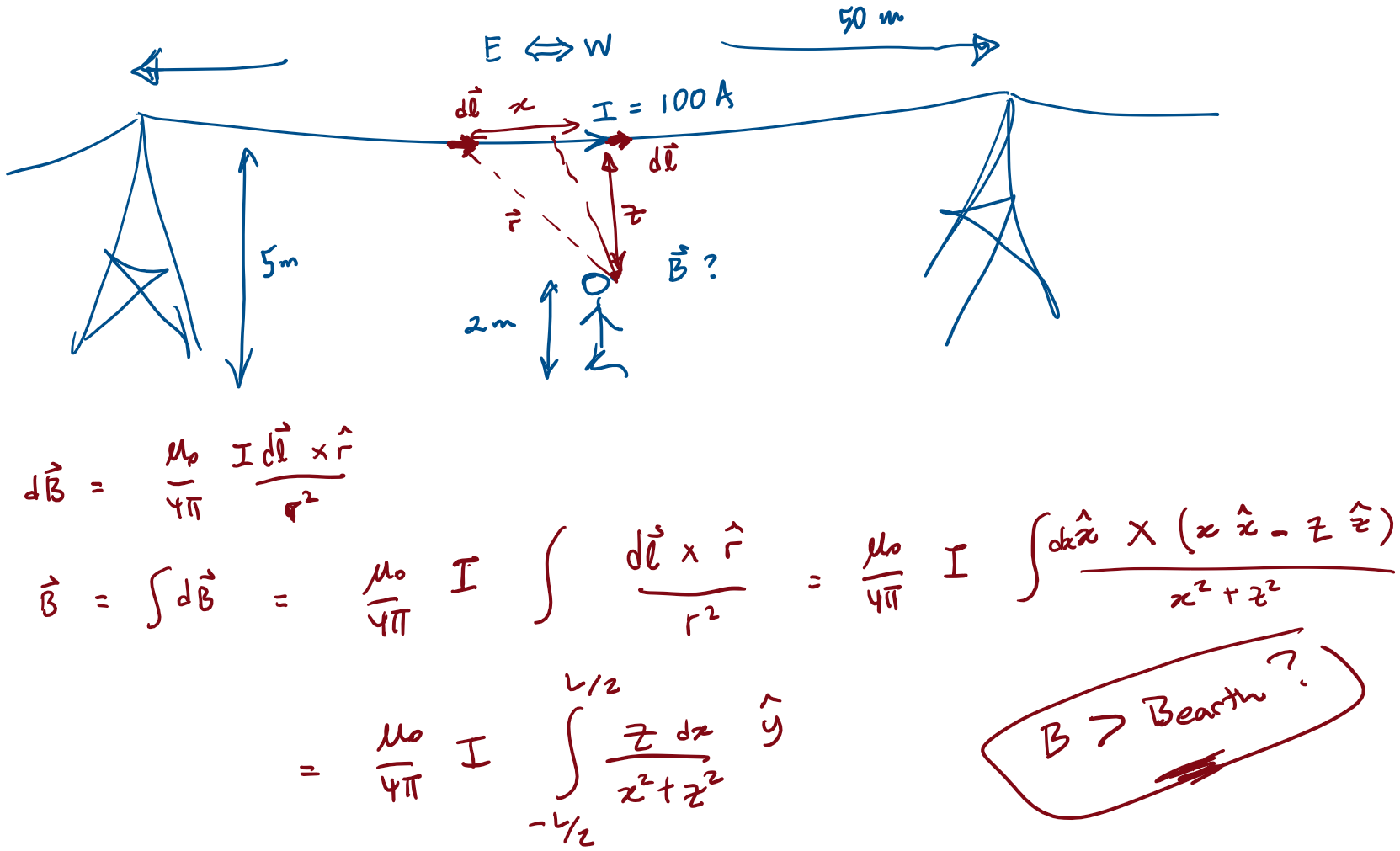
Example
Biot-Savart Law
d\vec{B}=\frac{\mu_0}{4\pi}\frac{I\ d\vec{l}\ \times \ \hat{r}}{r^2}
Magnetic Field due to a Current Segment
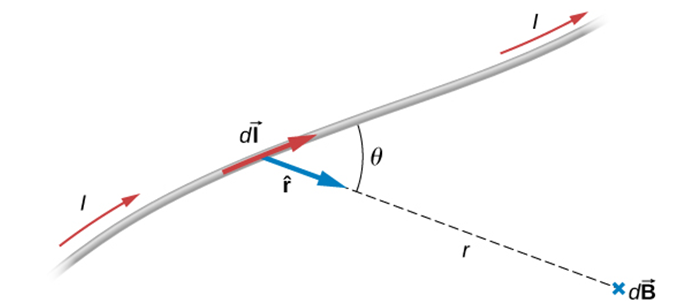
d\vec{B}=\frac{\mu_0}{4\pi}\frac{I\ d\vec{l}\ \times \ \hat{r}}{r^2}
\vec{B}=\frac{\mu_0}{4\pi}\frac{q\ \vec{v}\ \times \ \hat{r}}{r^2}
q \vec{v} = q \frac{d\vec{l}}{dt} = I\ d\vec{l}
Biot-Savart Law
d\vec{B}=\frac{\mu_0}{4\pi}\frac{I\ d\vec{l}\ \times \ \hat{r}}{r^2}
Magnetic Field due to a Current Segment