Atomic models

The evolution of atomic models at the beginning of the 20th century

Atomic models

Overview

Thomson's model

Bohr's model

deBroglie's contribution

Rutherford's model

Evidence in 1900 indicated that the atom was not a fundamental unit:

There seemed to be too many kinds of atoms, each belonging to a distinct chemical element.
Atoms and electromagnetic phenomena were intimately related (magnetic materials; insulators vs. conductors; different emission spectra).
Elements combine with some elements but not with others, a characteristic that hinted at an internal atomic structure (valence).
The discoveries of radioactivity, x-rays, and the electron (all seemed to involve atoms breaking apart in some way).

overview

We will follow the progression of atomic modeling in the early 20th century

Atomic models

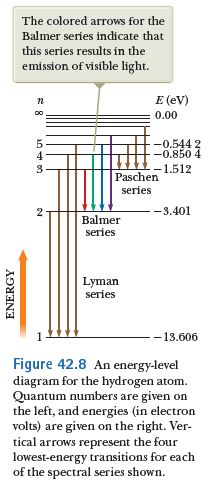
just a bit more about atomic spectra

Balmer series (1885)

\lambda = 364.6 \text{nm} \left(\frac{k^2}{k^2-4}\right)

Empirically, Balmer found an expression for the pattern of wavelengths in the Hydrogen spectrum

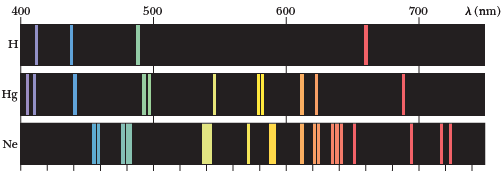
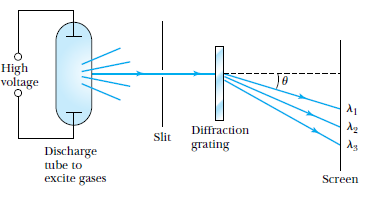
using a diffraction grating (fancy prism) that we are able to separate a beam of light into its spectral components

and that the emission spectra from different elements showed different components

Recall

\text{where} \quad k=3,4,5, ...

\text{e.g.}\quad k=3 \implies\lambda = 364.6 \text{nm} \left(\frac{3^2}{3^2-4}\right)=656.3\text{nm}

Atomic models

just a bit more about atomic spectra

Rydberg and Ritz (1890)

\frac{1}{\lambda} = \frac{1}{364.6 \text{nm}} \left(\frac{k^2-4}{k^2}\right)=\frac{4}{364.6 \text{nm}} \left(\frac{1}{2^2}-\frac{1}{k^2}\right)

Rydberg and Ritz recognized that Balmer's result can be expressed as:

\frac{1}{\lambda} = R_H\left(\frac{1}{n^2}-\frac{1}{k^2}\right)

Which generalizes to

\text{where} \quad R_H=1.0968 \times10^7 m^{-1}

Atomic models

Early atomic models

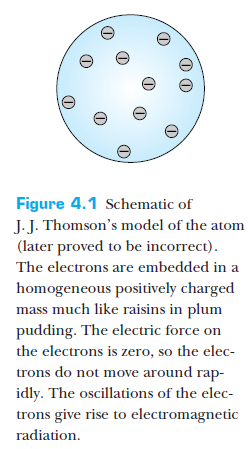
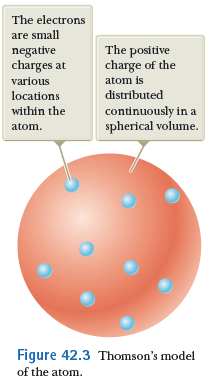
Thomson's model

Atomic models

Early atomic models

Thomson's model

Electrons (discovered in 1897) carry negative charge and are very light compared to atomic masses.

To achieve net charge neutrality, atoms must also contain positive charge.

The majority of the atomic mass is distributed over a large volume.

Electrons are fairly stationary within the atom, oscillating in place in accordance with temperature. Oscillations of electrons give rise to EM radiation.

This model can explain the variety of atoms.

Features of Thomson's model

Atomic models

Early atomic models

Thomson's model meets the real world.

Rutherford, Geiger, and Marsden used radioactive emission to study the structure of matter.

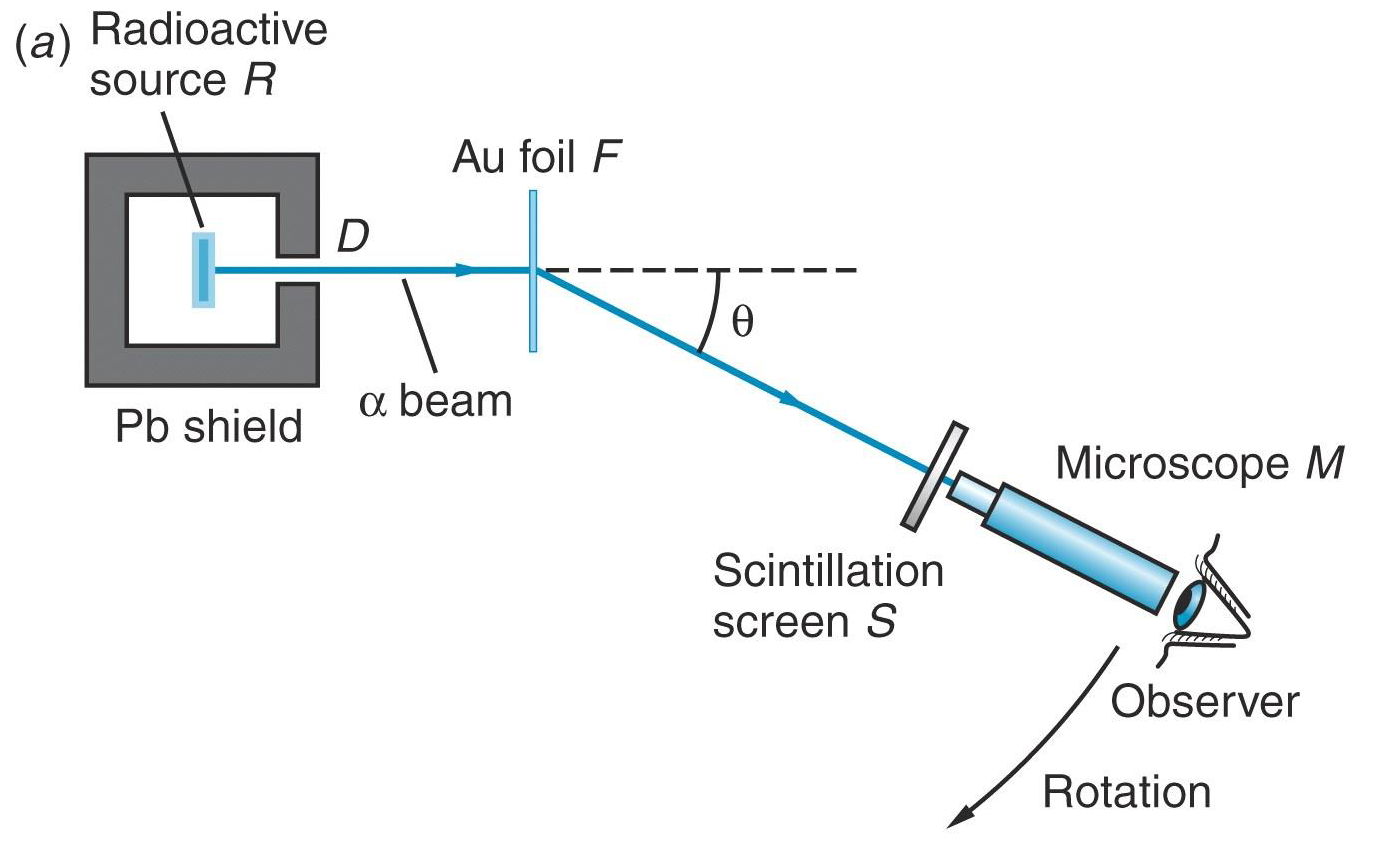
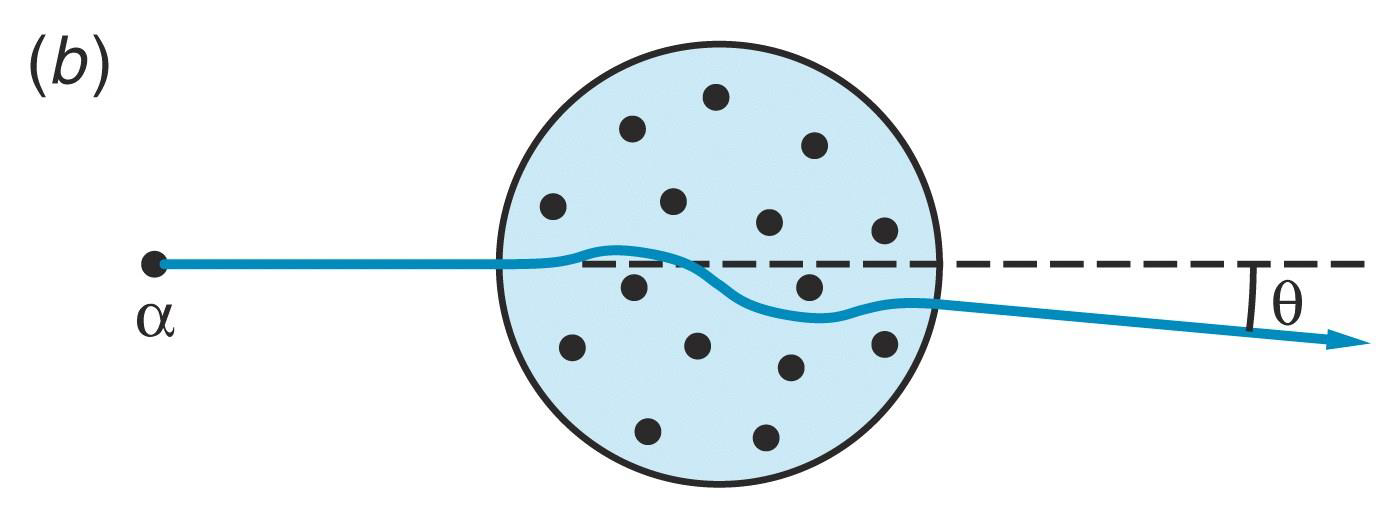
According to the Thomson model, the scattering angle of an alpha-particle from a gold atom would be very small.

However, experimental observations (in1909) of large-angle scattering were in direct disagreement with the predictions of Thomson's model.

Atomic models

Early atomic models

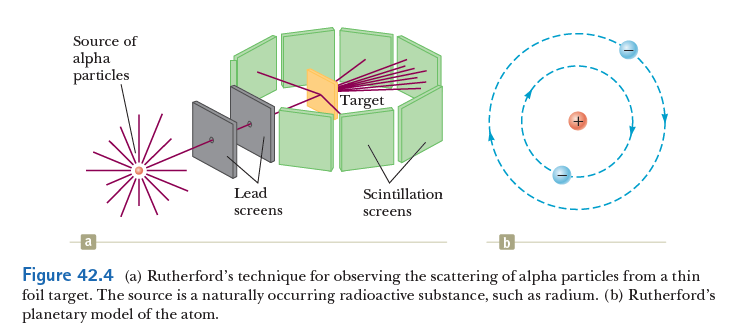
Rutherford's model

This suggested to Rutherford, that the positive charge must be concentrated in a small nucleus! Hence, the birth of the planetary model of the atom!

Atomic models

Early atomic models

Rutherford's scattering analysis

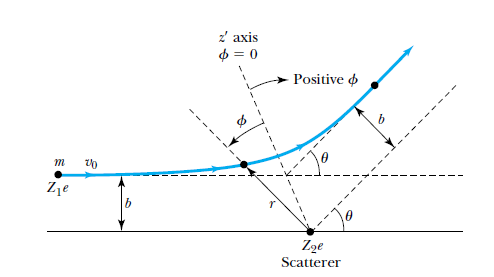
The nucleus is assumed to be a point charge.

The alpha particle is assumed to be a point charge, approaching in a path, which if not deflected, would pass at a distance from the nucleus known as the impact parameter.

The alpha particle and the nucleus interact with a Coulomb force, that ends up deflecting the alpha particle by some angle relative to its original path.

The geometry of Rutherford's scattering.

Atomic models

Early atomic models

Rutherford's scattering analysis

The physics of Rutherford's scattering.

The change in momentum manifests as a change of the direction of motion of the alpha particle.

The Coulomb force is inversely proportional to the square of the ever-varying distance between the alpha particle and the nucleus.

\vec{F} = \frac{1}{4\pi\epsilon_0}\ \frac{(Z_1 e) (Z_2 e)}{r^2}\ \hat{r}

\Delta \vec{p} =\int \vec F dt

The change in the alpha particle's momentum is equivalent to the impulse exerted on it by the nucleus:

Atomic models

Early atomic models

Rutherford's scattering analysis

In this model, the scattering angle is highly dependent on the impact parameter, and can indeed be quite large for small impact parameters.

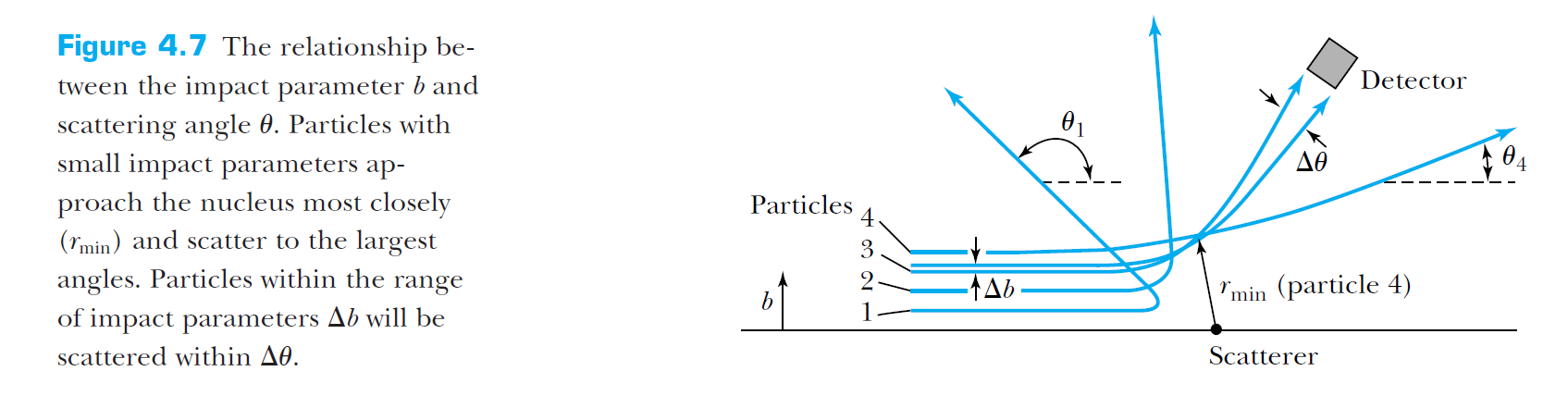
b = \frac{Z_1 Z_2 e^2}{8\pi\epsilon_0 K} \cot{ \frac{\theta}{2}}

Atomic models

Early atomic models

Rutherford's scattering analysis

Rutherford's model was successful in explaining the results of the scattering experiments.

Today, we know a lot more about the atomic nucleus; and one of the enduring ideas is that the nucleus contains most of the atomic mass in a volume that is a very small fraction of the size of an atom.

The spatial extension of a typical nucleus is ~ fm

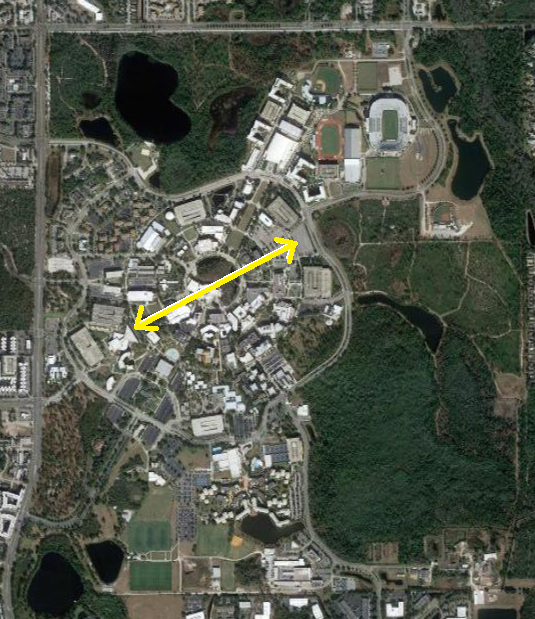
The comparative spatial extension of the atomic nucleus to the spatial extension of the electronic cloud in an atom is of the same order as the ratio of the size of your thumb compared to the size of UCF campus.

Atomic models

Early atomic models

The classical planetary model

In the planetary model: electrons carrying the negative charge, orbit the nucleus where the positive charge is concentrated, and the system is bound by the electrostatic potential.

Atomic models

Early atomic models

The classical planetary model

Atomic models

Early atomic models

The classical planetary model

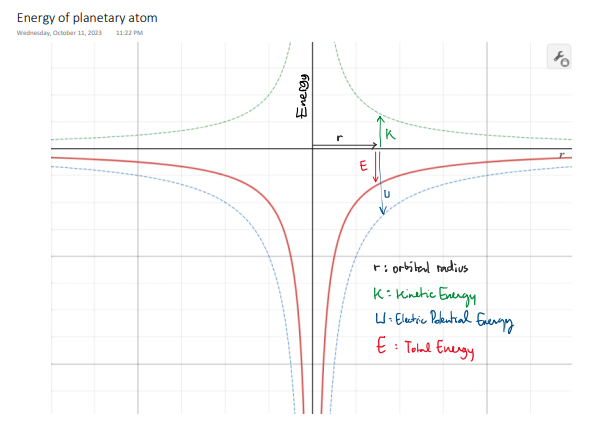
Let's examine the Hydrogen atom: 1 proton + 1 electron

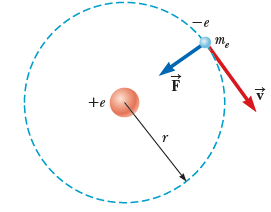
What is the total energy of the atom

(in the proton's frame)?

Atomic models

Early atomic models

The classical planetary model

Let's examine the Hydrogen atom: 1 proton + 1 electron

What is the total energy of the atom

(in the proton's frame)?

Electron's Kinetic Energy

K=\tfrac{1}{2}m_ev^2

=\tfrac{1}{2}m_e\frac{v^2}{r}r

=\frac{k e^2}{2r}

=\tfrac{1}{2}m_e a_c r

=\tfrac{1}{2}F_c r

=\tfrac{1}{2} \left( k \frac{|e \ (-e)|}{r^2}\right)r

Atomic models

Early atomic models

The classical planetary model

Let's examine the Hydrogen atom: 1 proton + 1 electron

What is the total energy of the atom

(in the proton's frame)?

Electron's Kinetic Energy

K

=\frac{k e^2}{2r}

Electric Potential Energy

U=k\frac{q_1\ q_2}{r}

=-k\frac{e^2}{r}

=k\frac{e\ (-e)}{r}

Atomic models

Early atomic models

The classical planetary model

Let's examine the Hydrogen atom: 1 proton + 1 electron

What is the total energy of the atom

(in the proton's frame)?

Electron's Kinetic Energy

K

=\frac{k e^2}{2r}

Electric Potential Energy

U=

=-\frac{ke^2}{r}

Total Energy

E=K+U

=\frac{ke^2}{2r}-\frac{ke^2}{r}

=-\frac{ke^2}{2r}

Atomic models

Early atomic models

The classical planetary model

Let's examine the Hydrogen atom: 1 proton + 1 electron

What is the total energy of the atom?

Electron's Kinetic Energy

K

=\frac{k e^2}{2r}

Electric Potential Energy

U=

=-\frac{ke^2}{r}

Total Energy

E

=-\frac{ke^2}{2r}

Atomic models

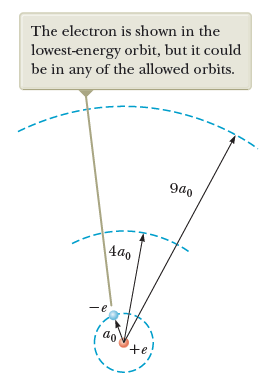
Bohr's model

Quantization of electronic orbits

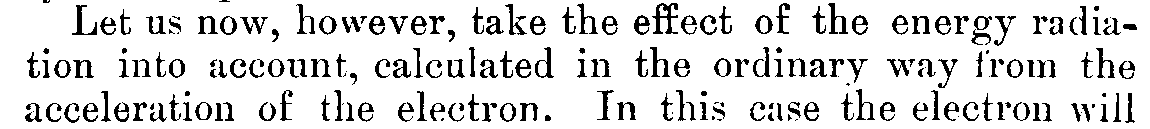
Atomic models

Bohr's model

Quantization of electronic orbits

Atomic models

Bohr's model

Quantization of electronic orbits

Bohr's model postulates:

Only certain "stationary states" exist in atoms.

In a stationary state, the electron does not radiate energy (as it would classically). The emission and absorption of radiation only occurs in conjunction with a transition between two stationary states.

These stationary states are determined by a condition imposed on the kinetic energy of the system, or equivalently -for circular orbits- a condition imposed on the electron's orbital angular momentum.

Atomic models

Bohr's model

Quantization of electronic orbits

Atomic models

Bohr's model

Quantization of electronic orbits

r_n=\frac{n^2\hbar^2}{kme^2}=n^2a_0

\text{where} \quad n=1,2,3,...

\text{and} \quad a_0=\frac{\hbar^2}{kme^2}=0.053\text{nm}

E_n=-\frac{k e^2 }{2r_n}=-\frac{1}{n^2}\frac{k e^2 }{2a_0}

=-\frac{13.606\ \text{eV }}{n^2}

\text{where} \quad n=1,2,3,...

Atomic models

Bohr's model

Transitions & atomic spectra

E_n=-\frac{1}{n^2}\frac{k e^2 }{2a_0}

E_i=E_f+E_\gamma

hf=\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\frac{k e^2 }{2a_0}

The conservation of energy dictates:

substituting

The transition of an atom from a higher-n state to a lower-n state is accompanied by the emission of a bundle of electromagnetic energy (photon):

\implies

E_n=-\frac{1}{n^2}\frac{k e^2 }{2a_0}

E_i+E_\gamma=E_f

hf=\left(\frac{1}{n_i^2}-\frac{1}{n_f^2}\right)\frac{k e^2 }{2a_0}

substituting

The absorption of a bundle of electromagnetic energy (photon) is accompanied by the transition of an atom from a lower-n state to a higher-n state:

\implies

Atomic models

Bohr's model

Transitions & atomic spectra

E_n=-\frac{1}{n^2}\frac{k e^2 }{2a_0}

E_i=E_f+E_\gamma

hf=\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\frac{k e^2 }{2a_0}

\frac{1}{\lambda}=\left(\frac{1}{n_f^2}-\frac{1}{n_i^2}\right)\frac{k e^2 }{2a_0hc}

\frac{1}{\lambda}=R_H\left(\frac{1}{n^2}-\frac{1}{k^2}\right)

So, to find the emission spectra:

substituting

or, in terms of the wavelength:

Which is identical to the form of the empirical expression

Success!!

Atomic models

Bohr's model

Heavier atoms

For an atom with Z protons

E_n=-\frac{Z^2}{n^2}\frac{k e^2 }{2a_0}

r_n=n^2\frac{a_0}{Z}

and

\text{where} \quad n=1,2,3,...

Atomic models

Bohr's model

Quiz

Name:

n_1=

n_2=

In Bohr's model of the Hydrogen atom, if the atom transitions from the n_1 electronic state to the n_2 state,

a) Does the atom absorb or emit energy?

b) Calculate the wavelength of the emitted/absorbed radiation.

Atomic models

Bohr's model

Quiz

Atomic models

Bohr's model

deBroglie's contribution

Matter waves

Atomic models

Bohr's model

deBroglie's contribution

Matter waves

Atomic models

Bohr's model

deBroglie's contribution

Using deBroglie's matter waves idea, and thinking of the orbiting electron as a standing wave:

2\pi r= n\lambda

2\pi r= n\frac{h}{p}

L=p\ r = n\frac{h}{2\pi}

L=n\hbar

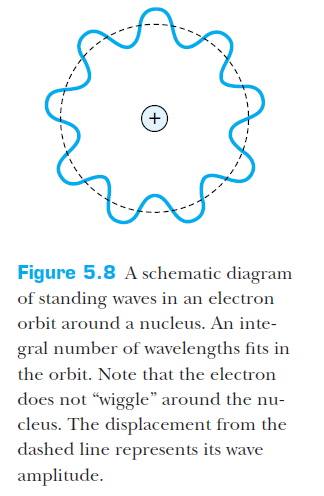
Orbit

circumference

integer number of wavelengths

=

Substitute the deBroglie wavelength of the electron

\lambda=h/p

Recall the definition of the orbital angular momentum

\vec{L}=\vec{p}\times\vec{r}