Electrostatics

When electricity is in charge

Electrostatics

Background

...

 Electrostatics

      Electric Charge

           ... is fundamental

Once upon a time ...

Experimental basis of QM

    Discovery of the X Ray and the Electron

          Thomson's experiment -- electron charge to mass ratio (1897)

From T & R, p 86

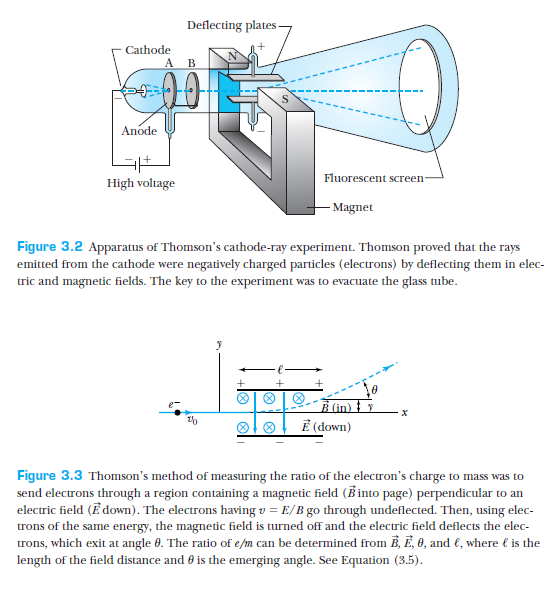
J.J. Thomson showed that cathode-rays were charged particles by showing their deflection in magnetic/electric fields.

Furthermore, he managed to measure the charge to mass ratio of the electron.

Experimental basis of QM

    Discovery of the X Ray and the Electron

          Thomson's experiment -- electron charge to mass ratio (1897)

From T & R, p 86

Experimental basis of QM

    Determination of the electron charge

          Millikan's experiment -- electron charge (1911)

From T & R, p 89

Millikan suspended oil drops between two plates by changing the potential difference across the plates.

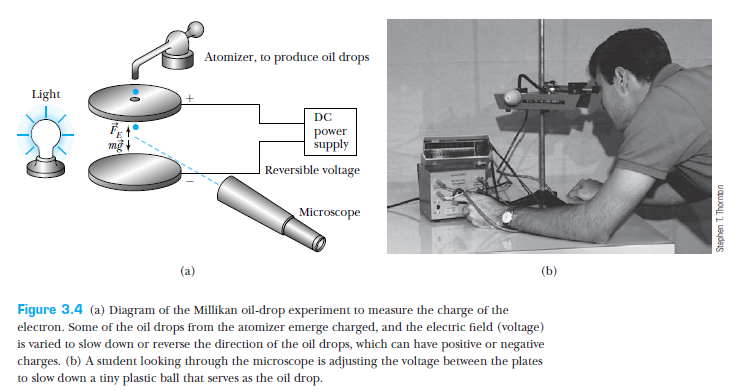
The equilibrium between the force of gravity and the electric force gave an estimate of the charge on the oil drop, in terms of its volume.

The volume was estimated from the terminal velocity.

Millikan found that the drops carried electric charge that was quantized!

The elementary charge, he found, was

e=1.602\times10^{-19}C

more on wikipedia

Experimental basis of QM

    Determination of the electron charge

          Millikan's experiment -- electron charge (1911)

 Electrostatics

      Electric Charge

           ... is fundamental

Once upon a time ...

The atomic nucleus

What lies within?

The variety of nuclei

Atomic Nucleus

      Nucleons & their structure

           Rutherford

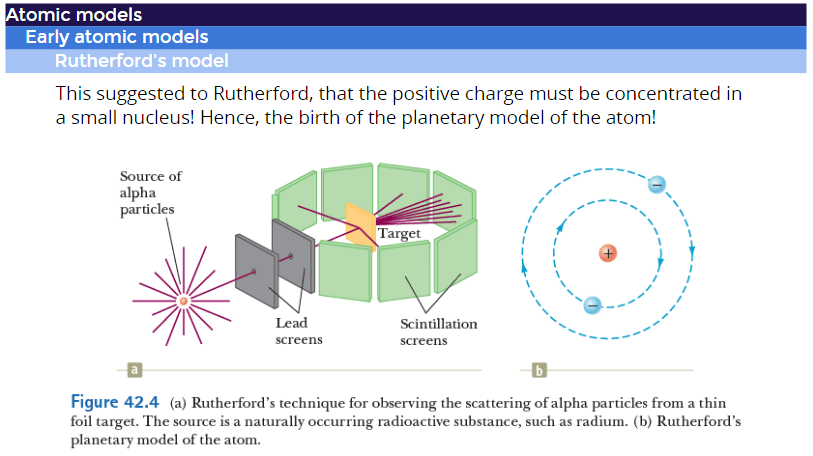
Once upon a time ...

Atomic Nucleus

      Nucleons & their structure

           Discovery of the neutron (1932)

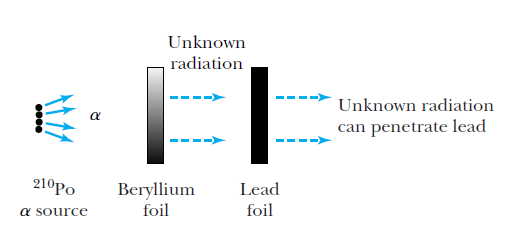
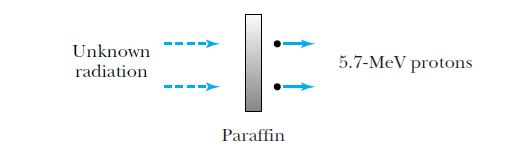
James Chadwick

Chadwick suggested the radiation was a neutral particle

of about the same mass as a proton.

Atomic Nucleus

           Chart of the nuclides

      The variety of nuclei

Atomic Nucleus

           Chart of the nuclides

      The variety of nuclei

Atomic Nucleus

           Chart of the nuclides

      The variety of nuclei

Atomic Nucleus

      The variety of nuclei

           Definitions

Isotope:

Atoms with same Z but different A

Nuclide:

A nuclear species with a given Z, N, and A

Isotone:

Atoms with same N but different A

Isobar:

Atoms with same A but different combination of Z and N

Atomic Nucleus

           Size of the nucleus 

Atomic nuclei are bound states of protons + neutrons

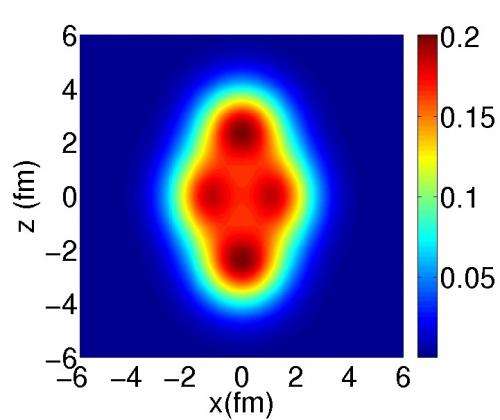
Probability density for the presence of neutrons and protons predicted for the neon-20 nucleus. It can be seen that this is not homogeneous: the neutrons and protons are distributed in clusters. © Jean-Paul Ebran/CEA

      Nucleons & their structure

The spatial extension of a typical nucleus is ~ fm

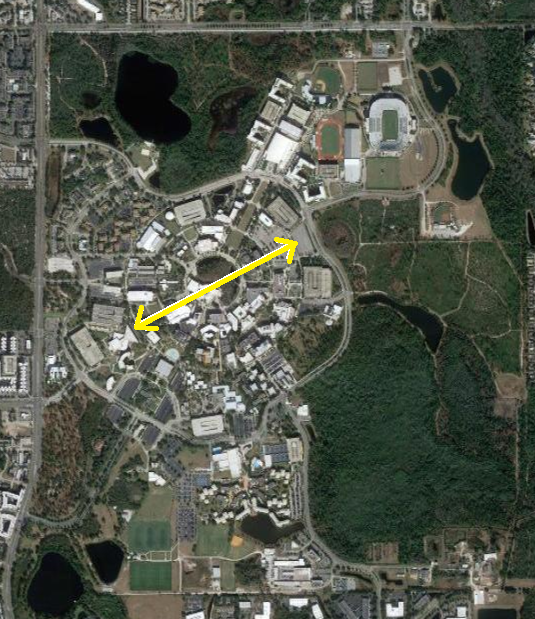
The comparative spatial extension of the atomic nucleus to the spatial extension of the electronic cloud in an atom is of the same order as the ratio of the size of your thumb compared to the size of UCF campus.

Atomic Nucleus

           Underlying structure

Atomic nuclei are bound states of protons + neutrons

Probability density for the presence of neutrons and protons predicted for the neon-20 nucleus. It can be seen that this is not homogeneous: the neutrons and protons are distributed in clusters. © Jean-Paul Ebran/CEA

protons & neutrons

have internal structure

      Nucleons & their structure

proton

neutron

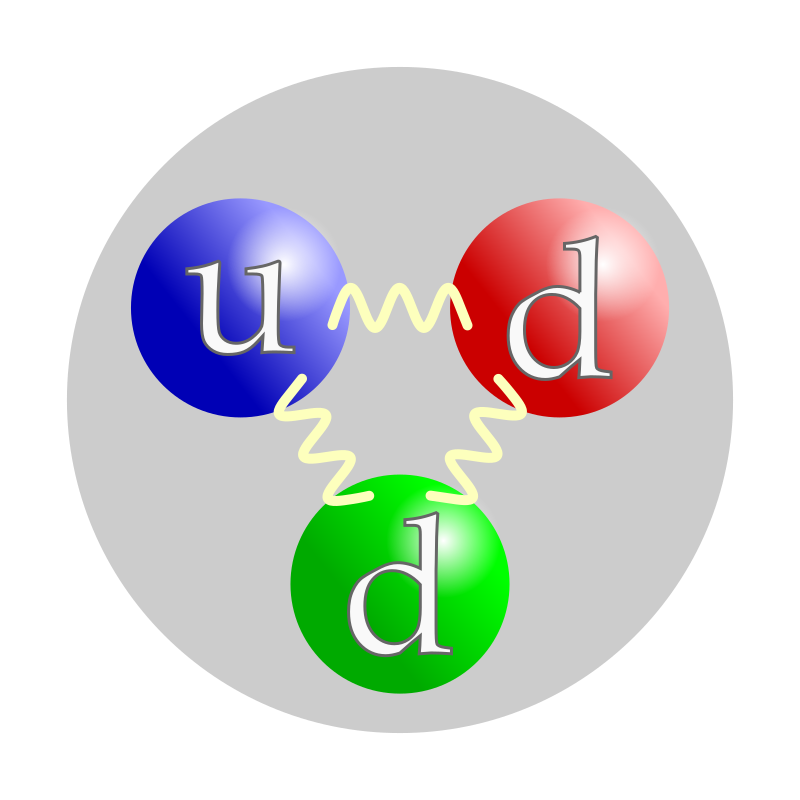
Atomic Nucleus

           Underlying structure

The Standard Model

of Elementary Particles

      Nucleons & their structure

Electrostatics

The Electric Charge

... is fundamental

 Electrostatics

      Electric Charge

           TL;DR

  • Electric Charge is an intrinsic property of matter.
e=1.602\times10^{-19}C
  • Electric Charge is quantized (i.e. manifests in nature in integer multiples of the elementary charge:
  • We have identified two types of charge -- ka positive and negative.
  • "Ordinary" matter is made up of atoms, who are themselves made up of protons, neutrons, and electrons. 
  • Neutral objects have equal number of protons and electrons. (neutral does not mean without charge.)

 Electrostatics

      Electric Charge

           The Net Electric Charge

  • Each Proton has a net charge of +e
  • Each Electron has a net charge of -e
  • Objects are charged by losing or gaining electrons.
  • Every ordinary object will carry a net charge that depends on the difference between the number of protons and electrons: 
q_\text{net}=n_p \times q_p + n_e \times q_e
=n_p \times e + n_e \times (-e)
=(n_p - n_e) \times e
  • Thus, an object will be negatively charged if it carries an excess of electrons, while a deficiency of electrons results in an overall positive net charge. 

 Electrostatics

      Electric Charge

           Charge Distributions

\lambda = dq / dl

Linear Charge Density

\sigma=dq / dA

Surface Charge Density

\rho=dq / dV

Volume Charge Density

\lambda_\text{\tiny uniform} = \frac{Q_\text{\tiny total}}{l_\text{\tiny total}}
\sigma\text{\tiny uniform} = \frac{Q_\text{\tiny total}}{A_\text{\tiny total}}
\rho\text{\tiny uniform} = \frac{Q_\text{\tiny total}}{V_\text{\tiny total}}

 Electrostatics

      Electric Charge

           Point Charge

Charge distribution A

Charge distribution B

What do we mean by point charges?

 Electrostatics

      Electric Charge

           Di-pole

What is an electric dipole?

Two equal but opposite charges separated by a small distance. 

The electric dipole moment 

The electric dipole moment p is a vector whose direction is from -q to +q and whose magnitude is given by p=qd

Electrostatics

The influence & interaction of electric charges

Overview

 Electrostatics

      The influence & interaction of electric charges

           The Cast 

electric charge

q
\vec{F}
\vec{E}
U
V
\Phi

electric charge influences

interaction between charges

Physical Quantities

 Electrostatics

      The influence & interaction of electric charges

           The Cast 

recurring roles

\vec{r}
\hat{r}
\hat{n}
\hat{r}=\frac{\vec{r}}{r} \text{ is a unit vector in direction of $\vec{r}$}
\text{ Relative Position Vector}

 Electrostatics

      The influence & interaction of electric charges

           The Cast 

charge

q
\vec{F}
\vec{E}
U
V
\Phi

influence

interaction

Physical Quantities

recurring roles

Parameters

\vec{r}
\hat{r}
\hat{n}
\hat{r}=\frac{\vec{r}}{r} \text{ is a unit vector in direction of $\vec{r}$}

 Electrostatics

      The influence & interaction of electric charges

           The Cast 

q
\vec{E}
V
\Phi

influence

interaction

Relationship Map

\ \vec{E}=-\vec{\nabla} V\
\ \Delta V = \int \vec{E}\cdot d\vec{s}\
\ \Phi = \int \vec{E}\cdot d\vec{A}\
\vec{F}
U
\ \vec{F}=-\vec{\nabla} U\
\ \Delta U = \int \vec{F}\cdot d\vec{s}\
\ \vec{F} = q_0\ \vec{E}\
\ \vec{E} = \vec{F}/q_0\ \
\ U = q_0\ V\
\ V = U/q_0\ \

 Electrostatics

      The influence & interaction of electric charges

           The Cast 

q
\vec{F}
U
\Phi

influence

interaction

Physical Quantities

\ \vec{E}=-\vec{\nabla} V\
\ \Delta V = -\int \vec{E}\cdot d\vec{s}\
\ \Phi = \int \vec{E}\cdot d\vec{A}\
\vec{E}
V
\ \vec{F}=-\vec{\nabla} U\
\ \Delta U = -\int \vec{F}\cdot d\vec{s}\
\ \vec{F} = q_0\ \vec{E}\
\ \vec{E} = \vec{F}/q_0\ \
\ U = q_0\ V\
\ V = U/q_0\ \

 Electrostatics

      The influence & interaction of electric charges

           The Cast 

m
\vec{F}_g
mgy
\Phi_g

influence

interaction

gravity

\ \vec{F}=-\vec{\nabla} (mgy)\\ =-mg\hat j
\ \Delta U = -\int \vec{F}\cdot d\vec{s}\
\ \Phi_g = \int \vec{g}\cdot d\vec{A}\
\vec{g}
gy
\ \vec{F}=-\vec{\nabla} U\
\ \Delta U = \int \vec{F}\cdot d\vec{s}\
\ \vec{F_g} = m\ \vec{g}\
\ \vec{g} = \vec{F_g}/m\ \
\ U_g = m\ V_g\
\ V_g = U_g/m\ \

electricity

implement toggle

Electrostatics

The influence of electric charges

The Electric Potential

 Electrostatics

      The Electric Potential

           Learning Outcomes

Learn how to:

Calculate the electric potential at a given point in space due to

  • a configuration of point charges.
  • a "continuous" distribution of electric charges.

 Electrostatics

      The Electric Potential

           Conceptual overview

Electric Charges have an influence in their vicinity that we call the Electric Potential.

imagine a hypothetical glow that depends on the charge distribution --

shape, sign, magnitude, ...

 Electrostatics

      The Electric Potential

           Conceptual overview

The Electric Potential due to some point charge is proportional to the magnitude of that charge.

The Electric Potential due to some electric charge is ...

The Electric Potential at some location due to some electric charge depends on the material(s) in the region(s) separating the charge and the measurement location.

inversely    proportional to the distance from that charge.

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon}\frac{q}{r}
\text{the Electric Potential due to a point-charge $q$ at some distance $r$}
\text{permittivity}
\text{SI unit: Volt (V)}
\text{Dimension: } \left [{M L^2}{T^{-2}C^{-1}}\right ]
\text{Scalar Quantity } (\pm)
\kappa : \text{relative permittivity (Dielectric Constant)}
\text{Permittivity of free space: } \epsilon_0=8.854\times10^{-12}\ Nm^2/C^2
\text{Absolute Permittivity (material dependent): } \epsilon = \kappa \epsilon_0

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon}\frac{q}{r}
\text{the Electric Potential from a point-charge $q$ at some distance $r$}

Visualizingthe Electric Potential from a point-charge (3D)

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon}\frac{q}{r}
\text{the Electric Potential from a point-charge $q$ at some distance $r$}

Visualizingthe Electric Potential from a point-charge (2D)

 Electrostatics

      The Electric Potential

           Point-charge

V(r)=\tfrac{1}{4\pi\epsilon}\frac{q}{r}
\text{the Electric Potential from a point-charge $q$ at some distance $r$}

Visualizingthe Electric Potential from a point-charge (1D)

 Electrostatics

      The Electric Potential

           Conceptual overview

The Potential "landscape"

 Electrostatics

      The Electric Potential

           Equipotential Surfaces

Equipotential

 Electrostatics

      The Electric Potential

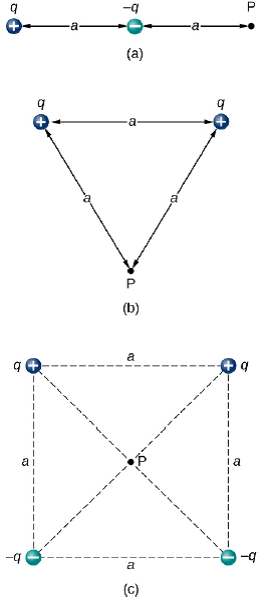
           Multiple point charges

V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}
\text{The Net Electric Potential due to multiple point-charges }
q_1
q_2
q_N
\text{algebriac sum}
\text{the contribution due to $q_i$}

 Electrostatics

      The Electric Potential

           Multiple point charges

V_\text{@ P}={\Large \Sigma}_{\tiny {i=1}} ^{\tiny N} \ \frac{k\ q_i}{r_i}
\text{The Net Electric Potential due to multiple point-charges }
q_1
q_2
q_N
\text{algebriac sum}
\text{the contribution due to $q_i$}

 Electrostatics

      The Electric Potential

            The Electric Potential Difference (aka Voltage)

\Delta V
\Delta V

ANALOG  VOLTMETER

 Electrostatics

      The Electric Potential

            The Electric Potential Difference (aka Voltage)

\Delta V
\Delta U= q \Delta V

Electrostatics

The influence of electric charges

The Electric Field

 Electrostatics

      The Electric Field

           Conceptual overview

The Potential "landscape"

\Delta V
\Delta s
\Delta V
\Delta s

Electrostatics

The influence of electric charges

Electric Force

 Electrostatics

      The Electric Force

           Coulomb's Law

Phenomenological approach

Summary of evidence from observations:

*Like charges repel, unlike attract

For point charges:

*Changing either charge changes the force proportionally. (e.g. doubling either charge doubles the force) 

*The force decreases as the distance between the charges increase, and vice versa.

*The force changes quadratically with the distance (e.g. halving the distance quadruples the force) 

 Electrostatics

      The Electric Force

           Coulomb's Law

\vec{F}_{ij}=\tfrac{1}{4\pi\epsilon_0}\frac{q_i\ q_j}{r^2_{\tiny ij}}\ \hat{r}_{\tiny ij}
\text{the electric force of $q_i$ on $q_j$}
\text{permittivity}
\text{ the distance between $q_i$ and $q_j$}
\text{ direction $i\rightarrow j$}
\text{ square}
\text{the charge exerting the force}
\text{the charge experiencing the force}
\left( k =\frac{1}{4\pi\epsilon_0} =8.99\times10^9 \quad \frac{\text{N$\cdot$ m$^2$}}{\text{C}^2}\right)
\epsilon_0 =8.85\times10^{-12} \quad \frac{\text{C}^2}{\text{N$\cdot$ m$^2$}}
\text{(free-space)}
\vec{F}_{q_i \text{ on } q_j}

 Electrostatics

      The Electric Force

           Coulomb's Law -- direction information

\vec{F}_{ij}=k\frac{q_i\ q_j}{r^2_{\tiny ij}}\ \blue{\hat{r}_{\tiny ij}}
\textcircled{\mathbf{\cdot}}
\textcircled{\cdot}
q_j
q_i
\hat{r}_{ij}
\vec{r}_{ij}
\vec{r}_{i}
\vec{r}_{j}
\hat{r}_{ij}\text{ is a unit vector in direction of $\vec{r}_{ij}$}
\text{ $\vec{r}_{ij}$ originates at $i$ and terminates at $j$}
\hat{r}_{ji}= -\hat{r}_{ij}
\vec{r}_{ij}= \vec{r}_{j}-\vec{r}_{i}
\vec{r}_{ji} = \vec{r}_{i}-\vec{r}_{j} =-( \vec{r}_{j}-\vec{r}_{i}) =-\vec{r}_{ij}
\vec{F}_{ji} = k\frac{q_j\ q_i}{r^2_{\tiny ji}}\ \blue{\hat{r}_{\tiny ji}} = k\frac{q_i\ q_j}{r^2_{\tiny ij}}\ \blue{(-\hat{r}_{\tiny ij})} =-\vec{F}_{ij}
\textcircled{\mathbf{\cdot}}
\textcircled{\cdot}
q_j
q_i
\hat{r}_{ji}
\vec{r}_{ji}
\vec{r}_{i}
\vec{r}_{j}
\hat{r}_{ij}=\frac{\vec{r}_{ij}}{r_{ij}}

 Electrostatics

      The Electric Force

           Coulomb's Law -- attraction & repulsion

q_j
q_i
\vec{F}_{ij}=k\frac{\blue{q_i\ q_j}}{r^2_{\tiny ij}}\ {\hat{r}_{\tiny ij}}
q_i\ q_j\gt 0
q_i\ q_j\lt 0
q_j
q_i
q_j
q_i
q_i
q_j
\vec{F}_{ij}
\vec{F}_{ij}
\vec{F}_{ij}
\vec{F}_{ij}
\hat{r}_{ij}
\hat{r}_{ij}
\hat{r}_{ij}
\hat{r}_{ij}
\textcircled{\mathbf{+}}
\textcircled{+}
\textcircled{\mathbf{-}}
\textcircled{-}
\textcircled{\mathbf{+}}
\textcircled{-}
\textcircled{\mathbf{-}}
\textcircled{+}
\textcircled{\mathbf{\cdot}}
\textcircled{\cdot}
q_j
q_i
\hat{r}_{ij}
\vec{r}_{ij}

 Electrostatics

      The Electric Force

           Coulomb's Law

\textcircled{\mathbf{+}}
\textcircled{-}
\textcircled{+}
\textcircled{-}

For a given configuration of point charges

q_1
q_2
q_4
q_3

 Electrostatics

      The Electric Force

           Coulomb's Law

\textcircled{\mathbf{+}}
q_1
\textcircled{-}
\textcircled{+}
q_2
\textcircled{-}
q_4
q_3

The interaction can be described in terms of force-pairs

\text{the electric force}
\text{of $q_4$ on $q_2$}
\text{the electric force}
\text{of $q_2$ on $q_4$}

 Electrostatics

      The Electric Force

           Coulomb's Law

\textcircled{-}
q_4

The net electric force on a charge of interest is the vector sum of all the electric forces acting on it.

\text{the electric force}
\text{of $q_2$ on $q_4$}
\textcircled{-}
q_4
\text{the electric force}
\text{the electric force}
\text{of $q_1$ on $q_4$}
\Sigma\vec{F}_\text{on $q_4$}
\vec{F}_\text{$q_1$ on $q_4$}
\vec{F}_\text{$q_2$ on $q_4$}
\vec{F}_\text{$q_3$ on $q_4$}
=
+
+
\text{of $q_3$ on $q_4$}
\Sigma \vec{F}_\text{on $q_4$}
\vec{F}_\text{$q_1$ on $q_4$}
\vec{F}_\text{$q_2$ on $q_4$}
\vec{F}_\text{$q_3$ on $q_4$}

 Electrostatics

      The Electric Force

           Coulomb's Law -- Check your understanding

\textcircled{\mathbf{+}}
\textcircled{-}
\textcircled{+}
\textcircled{-}
q_1
q_2
q_4
q_3
Made with Slides.com