Experimental basis of QM
A set of results that spawned 20th century physics
Experimental basis of QM
Overview
Experimental basis of QM
Setting the scene
Experimental basis of QM
Background
Electromagnetic waves
Experimental basis of QM
Status quo
Recall Maxwell's equations

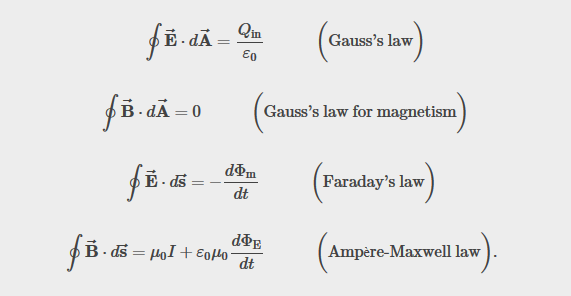
Experimental basis of QM
Status quo
Electromagnetic waves

we can scarcely avoid the conclusion that light consists in the transverse undulations of the same medium which is the cause of electric and magnetic phenomena
- Lecture at Kings College (1862)
This velocity is so nearly that of light, that it seems we have strong reason to conclude that light itself (including radiant heat, and other radiations if any) is an electromagnetic disturbance in the form of waves propagated through the electromagnetic field according to electromagnetic laws.
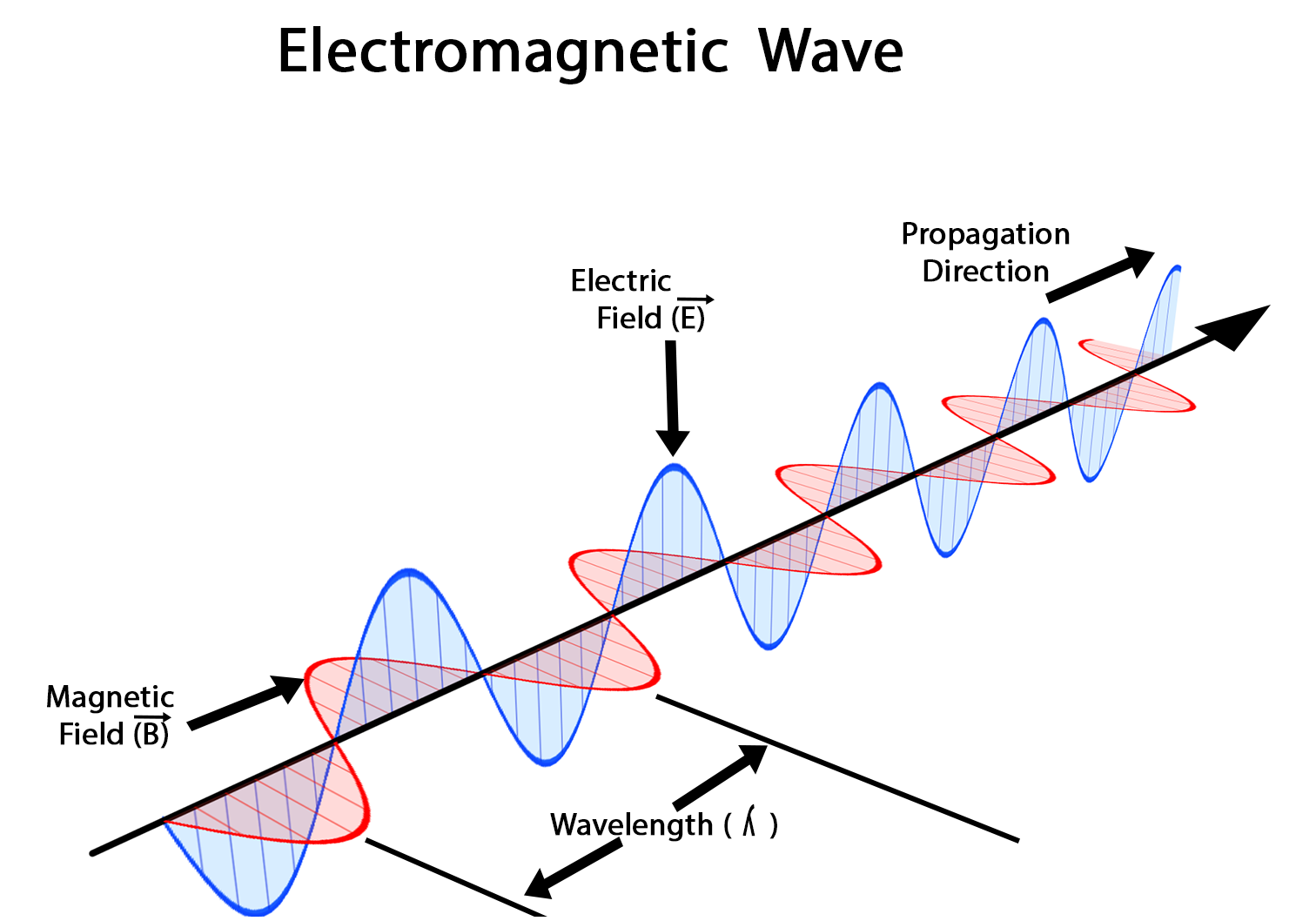
Experimental basis of QM
Status quo
Electromagnetic waves


Experimental basis of QM
Background
Emission spectra
Experimental basis of QM
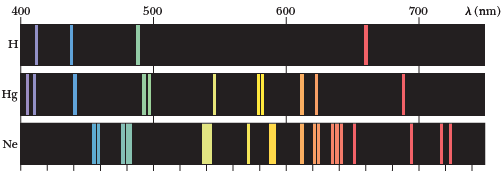
Line Spectra
Characteristic line spectra of elements
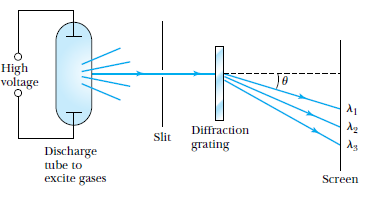

Experimental basis of QM
Line Spectra
Balmer series (1885)

Empirically, Balmer found an expression for the pattern of wavelengths in the Hydrogen spectrum

Experimental basis of QM
Line Spectra
Rydberg and Ritz (1890)
Rydberg and Ritz recognized that Balmer's result can be expressed as:

Which generalizes to
Experimental basis of QM
Background
Cathode Rays
Experimental basis of QM
Discovery of the X Ray and the Electron
Rontgen's (accidental) discovery of X-rays (1895)
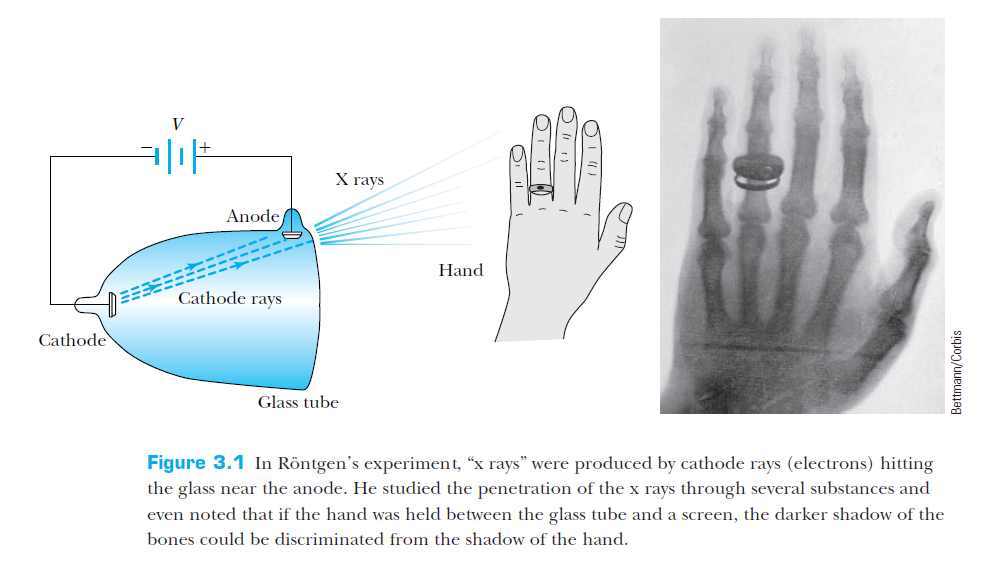
From T & R, p 86

Experimental basis of QM
Discovery of the X Ray and the Electron
Thomson's investigation of Cathode rays
Experimental basis of QM
Background
charge to mass ratio
Experimental basis of QM
Discovery of the X Ray and the Electron
Thomson's experiment -- electron charge to mass ratio (1897)
From T & R, p 86
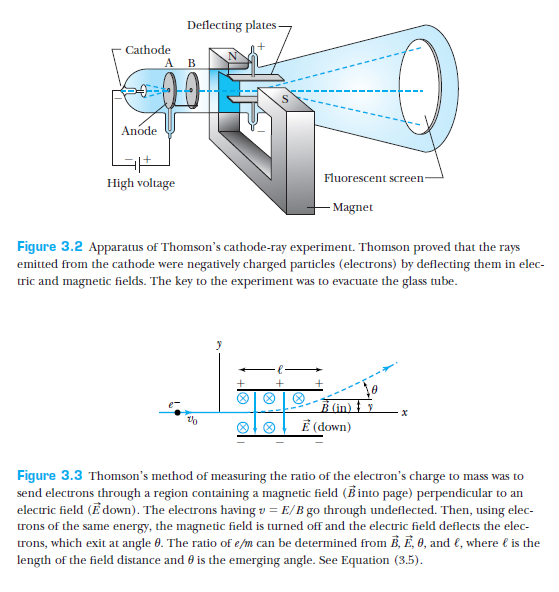
J.J. Thomson showed that cathode-rays were charged particles by showing their deflection in magnetic/electric fields.
Furthermore, he managed to measure the charge to mass ratio of the electron.
Experimental basis of QM
Discovery of the X Ray and the Electron
Thomson's experiment -- electron charge to mass ratio (1897)
From T & R, p 86

Experimental basis of QM
Background
Millikan's quantization of charge
Experimental basis of QM
Determination of the electron charge
Millikan's experiment -- electron charge (1911)
From T & R, p 89
Millikan suspended oil drops between two plates by changing the potential difference across the plates.
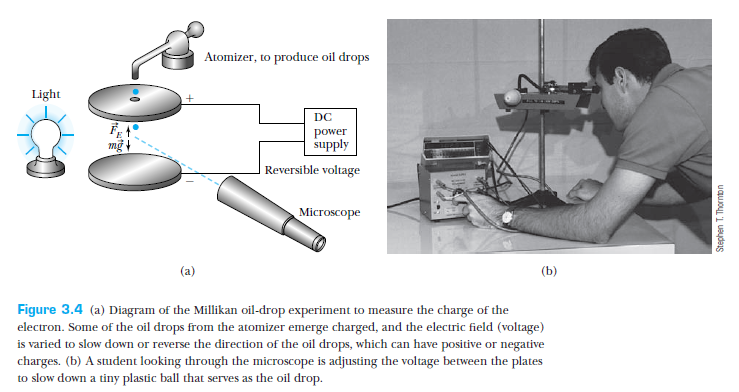
The equilibrium between the force of gravity and the electric force gave an estimate of the charge on the oil drop, in terms of its volume.
The volume was estimated from the terminal velocity.
Millikan found that the drops carried electric charge that was quantized!
The elementary charge, he found, was

Experimental basis of QM
Determination of the electron charge
Millikan's experiment -- electron charge (1911)
Experimental basis of QM
Blackbody Radiation and the birth of the quanta
Experimental basis of QM
Blackbody Radiation
What is a blackbody?
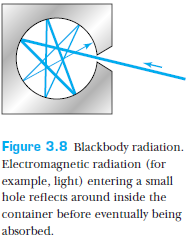
All bodies simultaneously emit and absorb radiation.
A blackbody absorbs all radiation that is incident on it, and reflects none.
A blackbody emits thermal radiation whose properties do not depend on the material, but rather on the temperature of the body.
Experimental basis of QM
Blackbody Radiation
Spectral distribution of blackbody radiation
Experimental basis of QM
Blackbody Radiation
Spectral distribution of blackbody radiation
The wavelength @ peak intensity shifts to smaller wavelengths for bodies with higher temperature.
The intensity is the total power radiated per unit area per unit wavelength at a given temperature.
The total power (per unit area) increases dramatically with temperature.
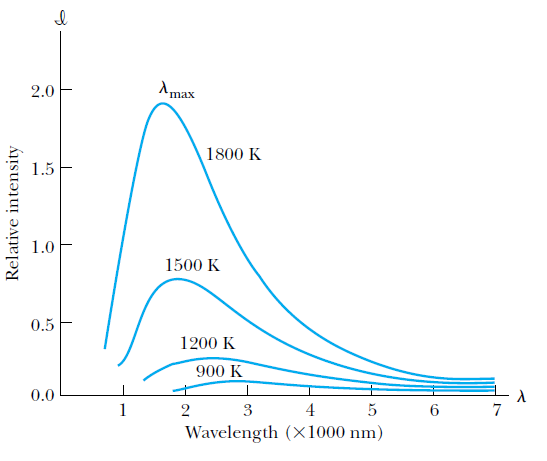
Spectral distribution of radiation emitted from a blackbody for different blackbody temperatures.
Experimental basis of QM
Blackbody Radiation
Spectral distribution of blackbody radiation
The wavelength @ peak intensity shifts to smaller wavelengths for bodies with higher temperature.
The total power (per unit area) increases dramatically with temperature.
Wien's displacement law
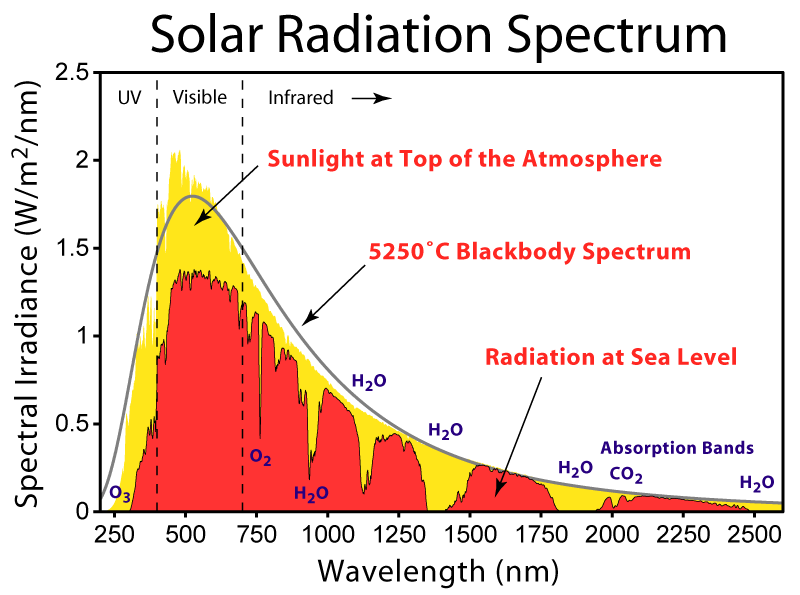

Q: Given this solar radiation spectrum, estimate the temperature of the surface of the sun.


Q: Estimate the peak wavelength at which a human body emits thermal radiation.

Q: What color signifies an object at a higher temperature? R or B?
Experimental basis of QM
Blackbody Radiation
Spectral distribution of blackbody radiation
The total power (per unit area) increases dramatically with temperature.
Stefan-Boltzmann law
for blackbody radiation
where
and
For any other body (other than a blackbody)
where
is the emmissivity, which depends on the surface material.

Experimental basis of QM
Spectral distribution of blackbody radiation
Empirical results
Q: Estimate the total power emitted by the sun, and the intensity of solar radiation on Earth.

Given
Experimental basis of QM
Spectral distribution of blackbody radiation
Empirical results
Q: Estimate the total power emitted by the sun, and the intensity of solar radiation on Earth.

Given
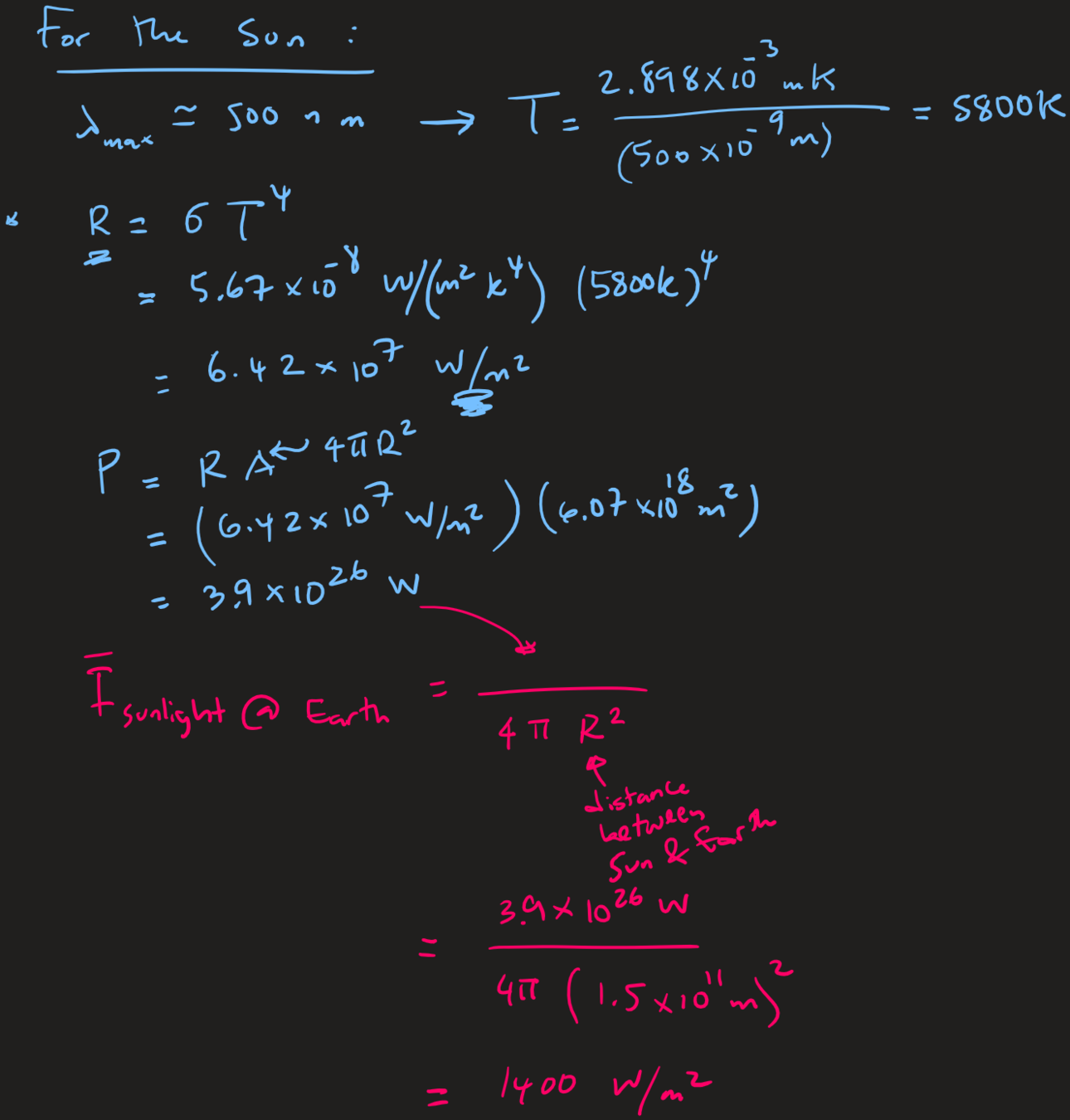
Experimental basis of QM
Spectral distribution of blackbody radiation
Empirical results
Q: Estimate the time it would take for the human body to radiate enough heat to drop from 37 degrees Celsius to 36 (in the absence of any other heat input or output.)
You will have to make some assumptions about:
- effective emissivity of body surface
- surface area of emitting body
- mass of body
- effective heat capacity of body
Approach:
- Estimate how much heat needs to be radiated, and
- estimate the rate at which humans radiate energy, then
- combine the two estimates for an estimate of the time.
Experimental basis of QM
Quantization of thermal energy spectrum
Spectral distribution of blackbody radiation
The culmination of classical physics attempting to describe thermal radiation of a blackbody
Rayleigh-Jeans formula
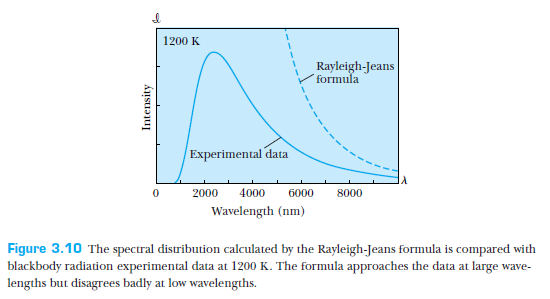
The ultraviolet catastrophe!
Experimental basis of QM
Quantization of Energy
Max Planck's Energy Distribution Law of thermal radiation



Experimental basis of QM
Quantization of Energy
Max Planck's quantization of energy

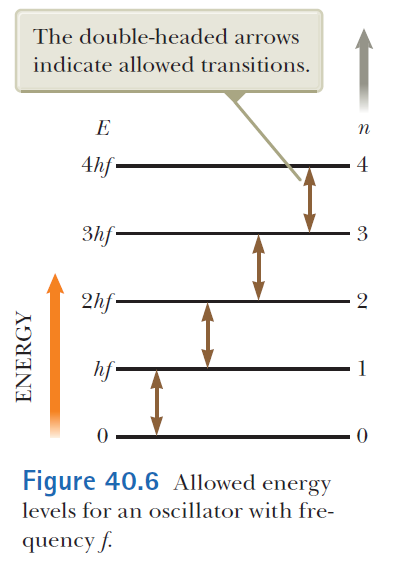
Blackbody radiation results from the transitions of quantized atomic oscillators.
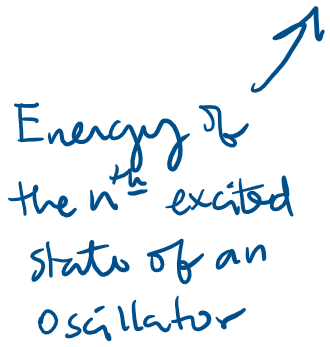
The energy of an oscillator can only have discrete values
The transitions between the discrete energies of an oscillator are


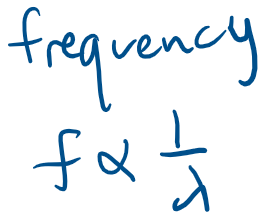


Experimental basis of QM
Quantization of energy
Max Planck's quantization of energy
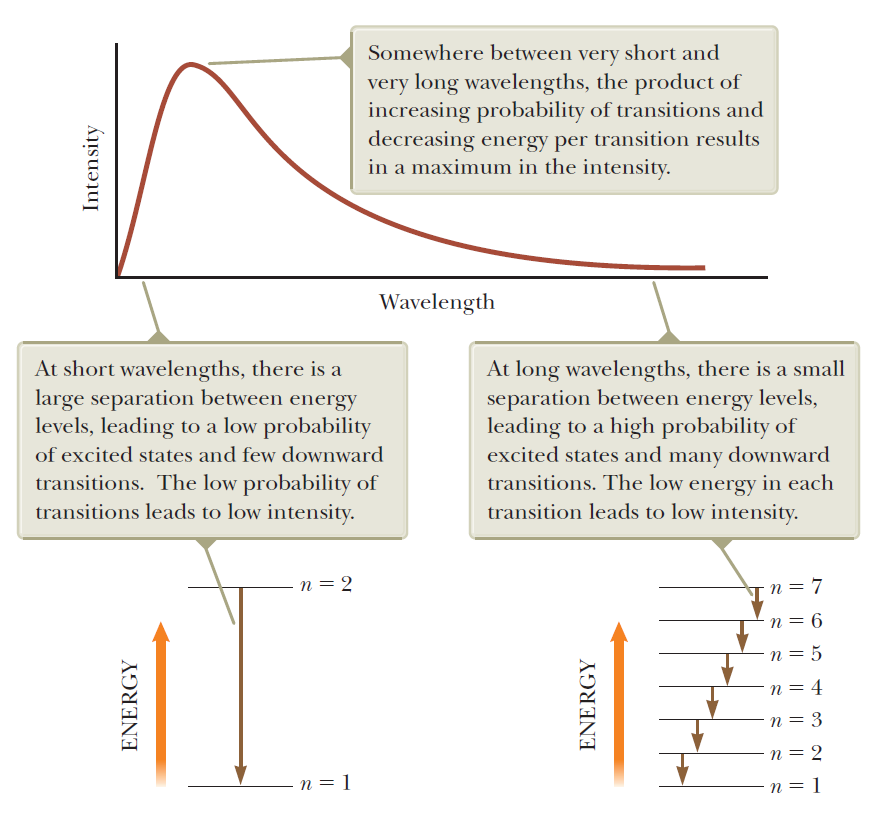
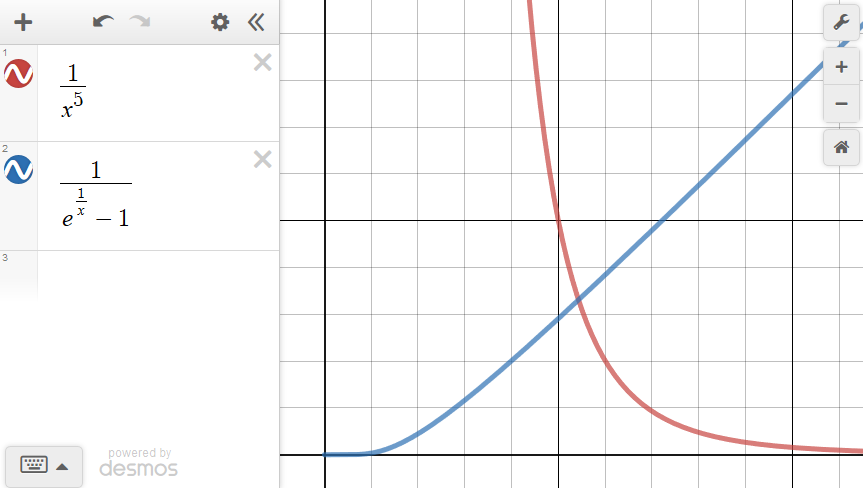

Experimental basis of QM
Quantization of energy
Max Planck's quantization of energy



Wien's displacement law
Experimental basis of QM
Quantization of energy
Max Planck's quantization of energy



Stefan-Boltzmann law
Experimental basis of QM
Quantization of energy
Max Planck's quantization of energy


Q: For a black body at temperature of T_0, what percentage of its emitted thermal radiation has a frequency higher than f_0?
where
Experimental basis of QM
Quantization of energy
Max Planck's quantization of energy
Experimental basis of QM
The photoelectric effect and its implications
Experimental basis of QM
Quantization of light energy
The photoelectric effect
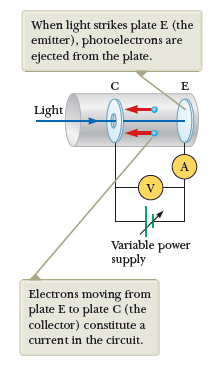
Classically, electrons absorb energy continuously from the incident electromagnetic waves, so you would expect:
- As the intensity of the light increases, energy would be transfered at a higher rate, and therefore ejected electrons will have higher kinetic energy.
- Electrons should be ejected from the metal at any incident frequency of light, as long as the intensity is high enough.
- The kinetic energy of the electrons only depend on intensity, and not on the frequency of the light.
Experimental basis of QM
Quantization of light energy
The photoelectric effect

According to the quantum description, by Einstein, an incoming photon gives all its energy to a single electron, thus energy is absorbed by the metal in bundles, not continuously.
- The kinetic energy of the ejected electron is dependent on the incoming photon's energy (which is proportional to its frequency), not on the intensity.
- The intensity of the light determines the number of photons, and therefore the number of ejected electrons.
Experimental basis of QM
Quantization of light energy
The photoelectric effect
Experimental basis of QM
Quantization of light energy
The photoelectric effect
Experimental basis of QM
Quantization of light energy
The photoelectric effect
Observations:
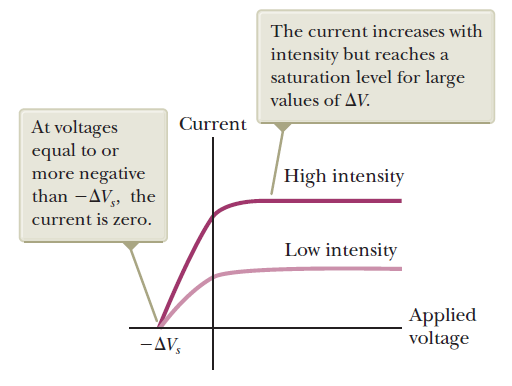
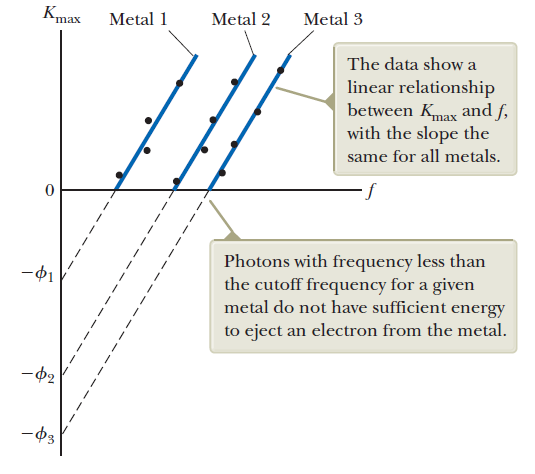
Experimental basis of QM
Quantization of light energy
The photoelectric effect

Suppose a Sodium surface is illuminated with light of wavelength = 300 nm. What is the maximum kinetic energy of the ejected electrons?
Example
Experimental basis of QM
Quantization of light energy
The photoelectric effect
The threshold wavelength of potassium is 558 nm. What is the work function for potassium? What is the stopping potential when light of wavelength 400 nm is used?
Example
Experimental basis of QM
Quantization of light energy
The photoelectric effect

Experimental basis of QM
Compton's Scattering
Experimental basis of QM
Quantization of light Energy
Photon momentum
Recall
and for photons
But, according to Planck,
Therefore, for photons
Experimental basis of QM
Quantization of light energy
Compton's Scattering
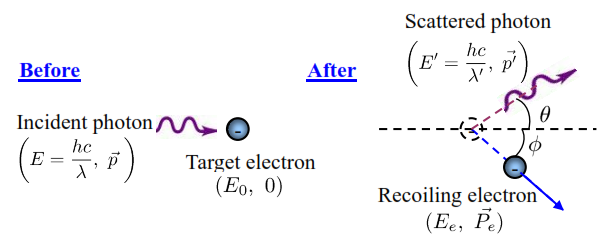
In an elastic collision between a photon and a free electron:
The conservation of momentum leads to:
Experimental basis of QM
Quantization of light energy
Compton's Scattering

In an elastic collision between a photon and a free electron:
The conservation of momentum leads to:
The conservation of Energy leads to:
Experimental basis of QM
Quantization of light energy
Compton's Scattering

In an elastic collision between a photon and a free electron:
combining
The conservation of momentum leads to:
The conservation of Energy leads to:
Experimental basis of QM
Quantization of light energy
Compton's Scattering

In an elastic collision between a photon and a free electron:
The conservation of energy and momentum lead to:
i.e. If the analysis is correct, we should find a specific correlation between the angle of ricochet and the scattered photon's wavelength.
Experimental basis of QM
Quantization of light energy
The Compton effect
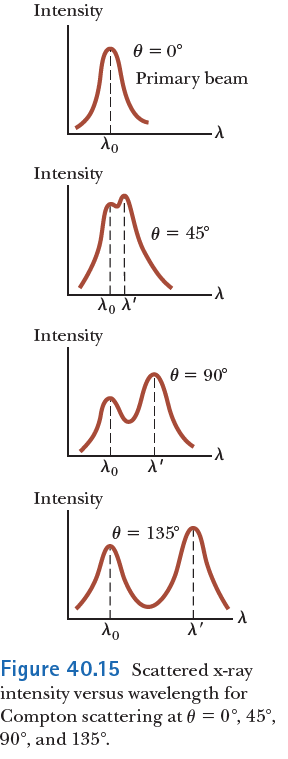
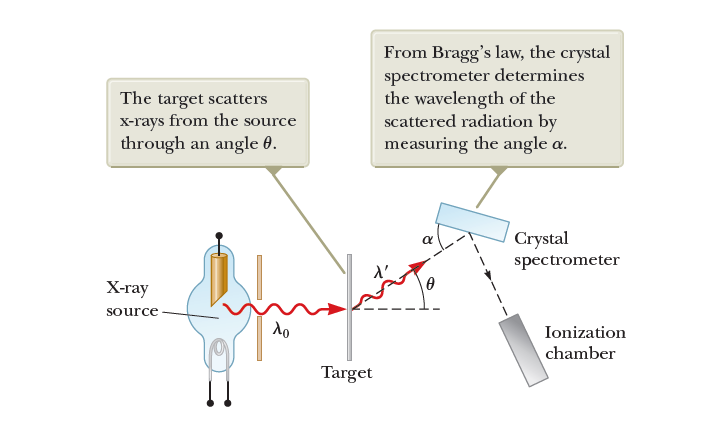
Compton verified this result experimentally, finding scattered photons with specific wavelengths at specific angles.
Experimental basis of QM
Quantization of light energy
The Compton effect
Suppose an x-ray photon with wavelength of 0.0500 nm loses 4% of its energy in a collision with an electron that is initially at rest. At what angle does the photon deflect (from its original trajectory)?
Example