Intro to Quantum Mechanics - part I
Wave properties of matter and the birth of Quantum Mechanics
Intro to Quantum Mechanics - part I
Wave properties of matter and the birth of Quantum Mechanics
When matter behaves like waves
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
Electron Diffraction
Recall de Broglie's result:
every entity, which we previously thought of as a particle, also exhibits wave behavior, with wavelength:
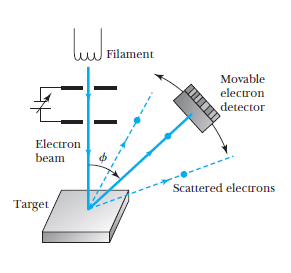

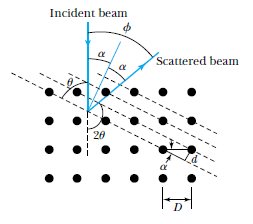
Example: Electron diffraction
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The double-slit experiment
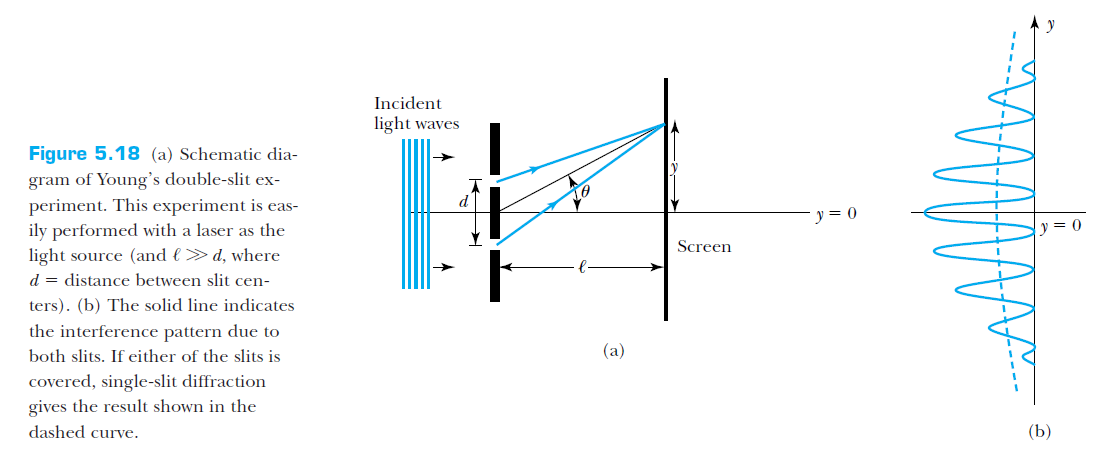
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The double-slit experiment

Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The double-slit experiment

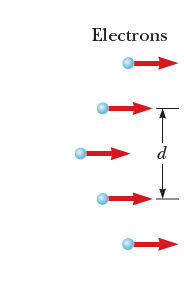
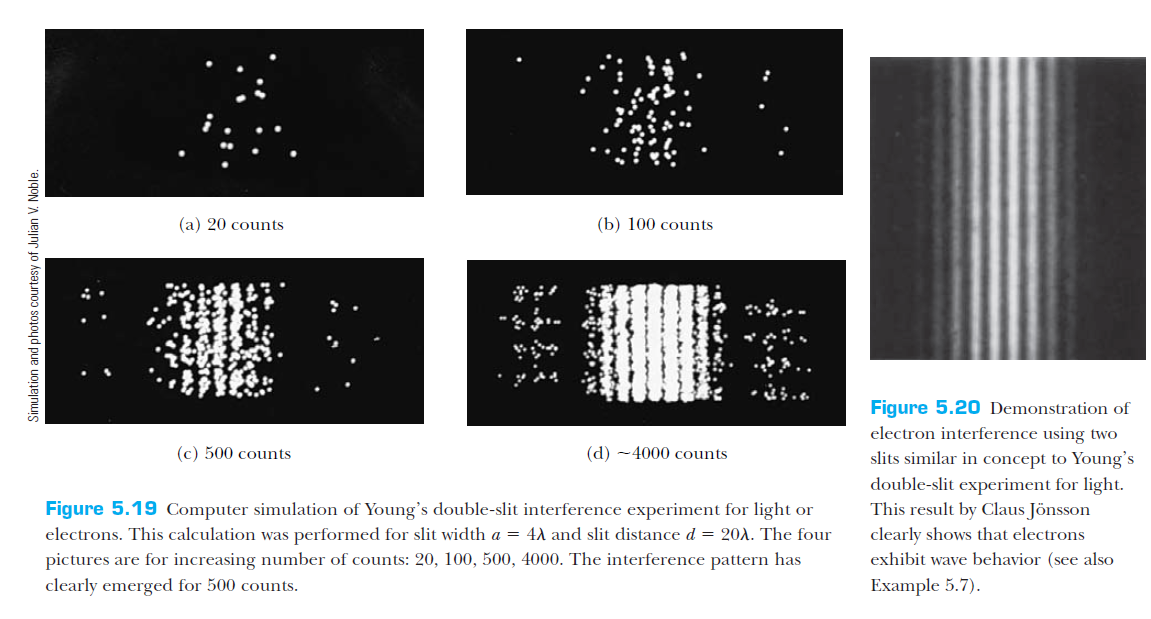
What happens if we repeat this experiment, but with electrons instead of light?
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The double-slit experiment
Intro to Quantum Mechanics - part I
Wave properties of matter and the birth of Quantum Mechanics
Classical Waves
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
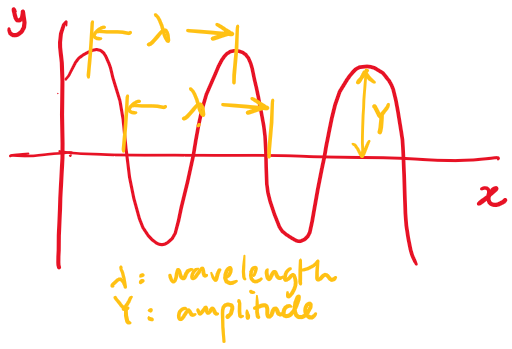
What is a wave?
Classically, a wave is defined as a traveling disturbance that carries energy.
E.g. a wave on a string is a disturbance in the vertical position of the beads travelling along the string (via tension) carrying mechanical energy.
For a traveling harmonic wave
Describe the disturbance as a function of position at a specific instant in time.
where is the wavelength (distance from peak to peak in a snapshot)
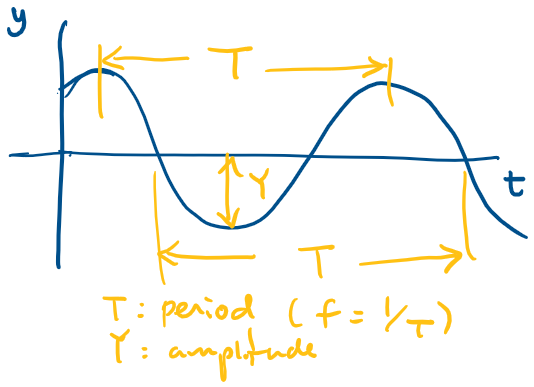
Describe the disturbance as a function of time at a specific location.
where is the period (time of one cycle, at a specific location.)
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
The wave equation
For a traveling harmonic wave
The Classical Wave Equation!
where:
: wave number
: angular frequency
: amplitude
: phase constant
Q: find the relationship between
and
Intro to Quantum Mechanics - part I
Wave properties of matter and the birth of Quantum Mechanics
Wave Packets
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
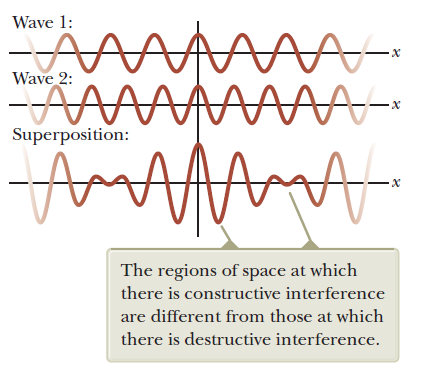
Superposition of two waves
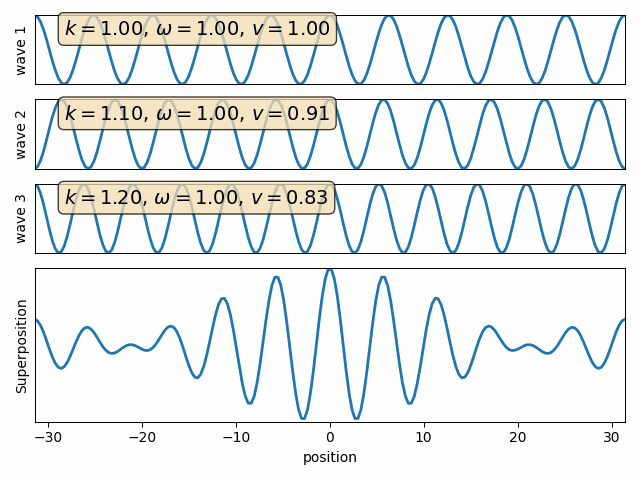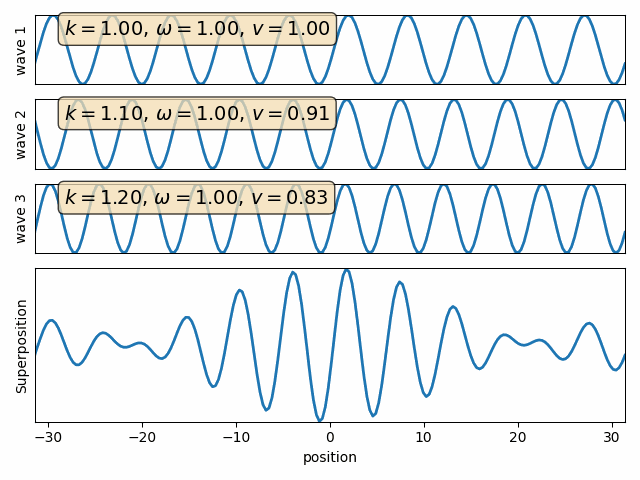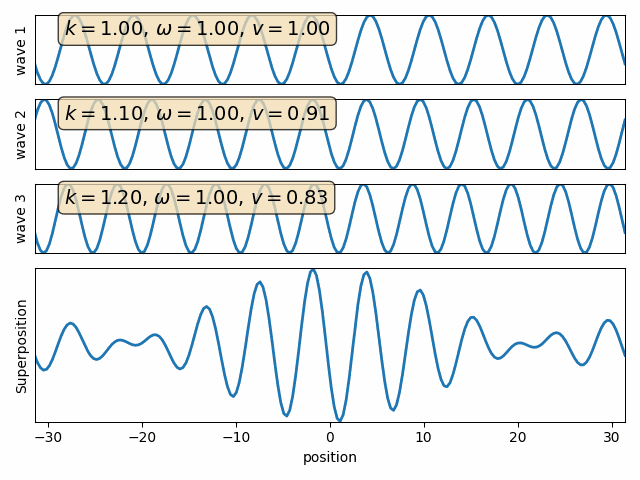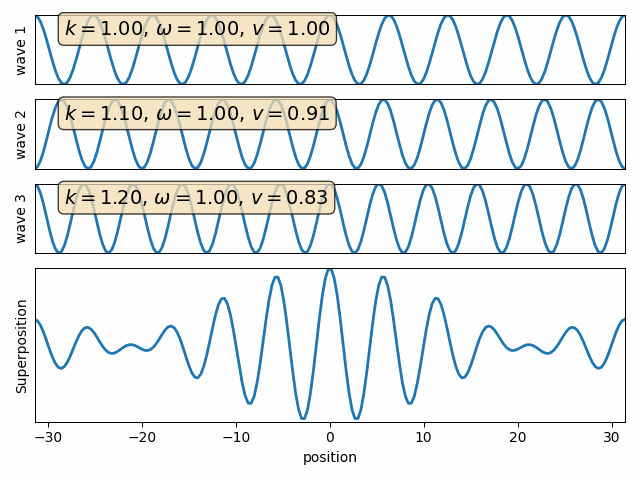
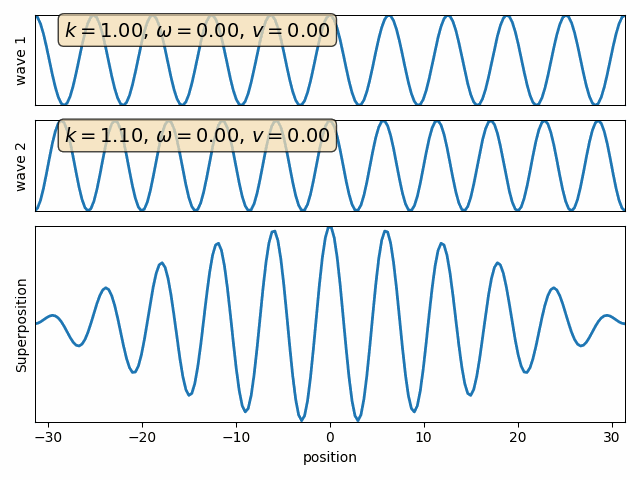
Q: find the sum of two waves with different wave numbers and angular frequencies. (assume both phase angles are 90)
Wave 1
Wave 2
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Superposition of two waves
Wave 1
Wave 2
carrier
envelope
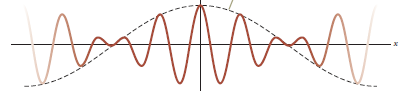
Attention: This snapshot is at t=0
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
The wave packet
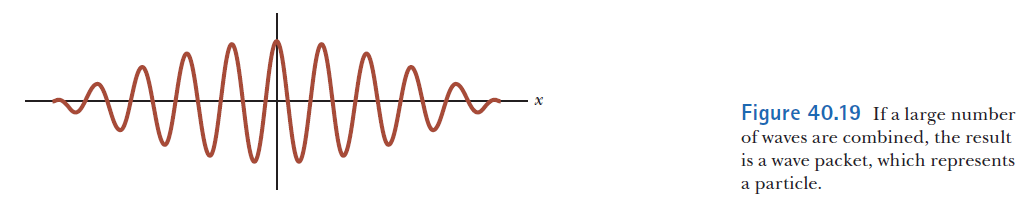
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
The wave packet
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
The wave packet
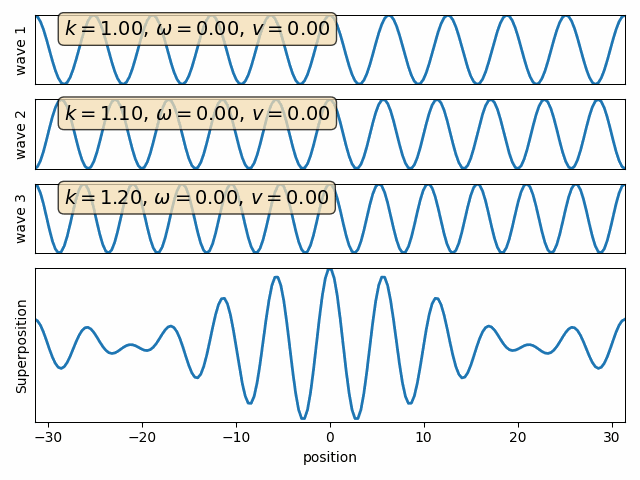
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
The wave packet
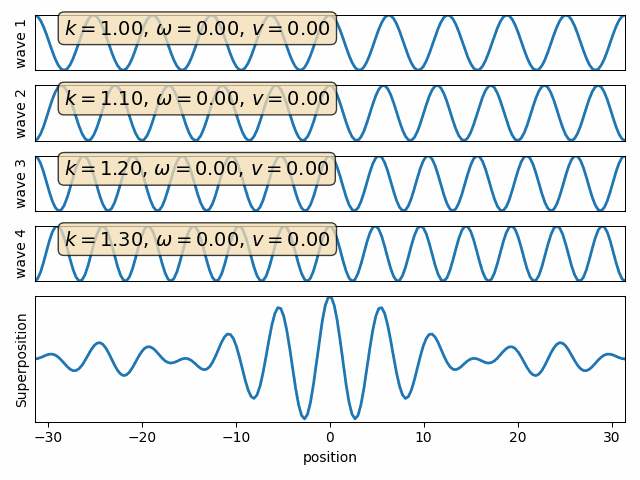
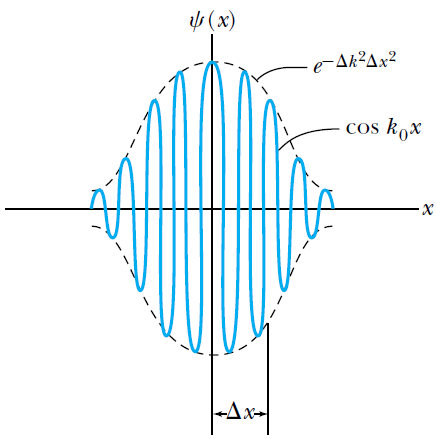
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
The gaussian wave packet
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Phase velocity and Group velocity
In a wave packet,
the velocity of some component
is given by
This is known as phase velocity, because it is the rate of advance of a point with a fixed phase (e.g. crest of the wave.)
As for the full packet, the relevant velocity is that of the envelope. This is known as group velocity, and is given by
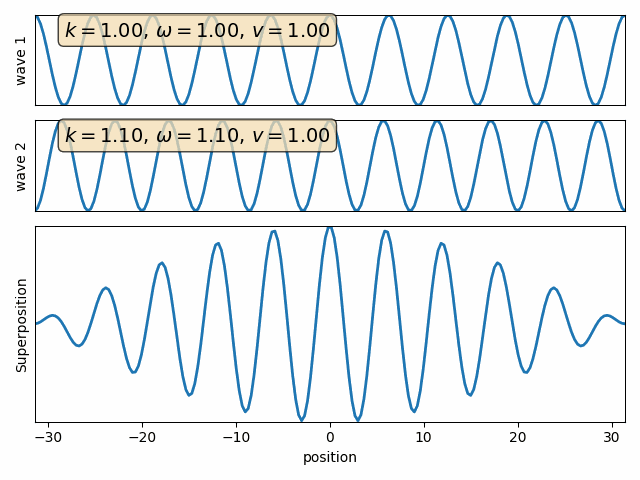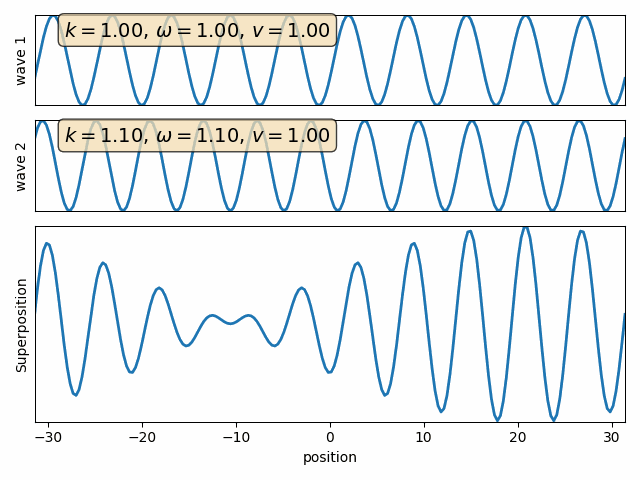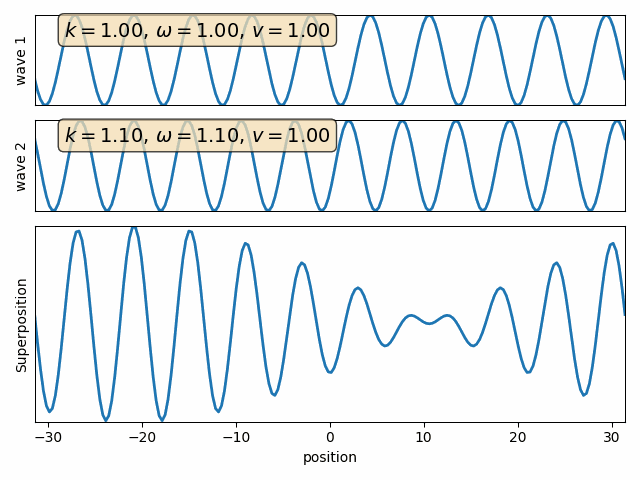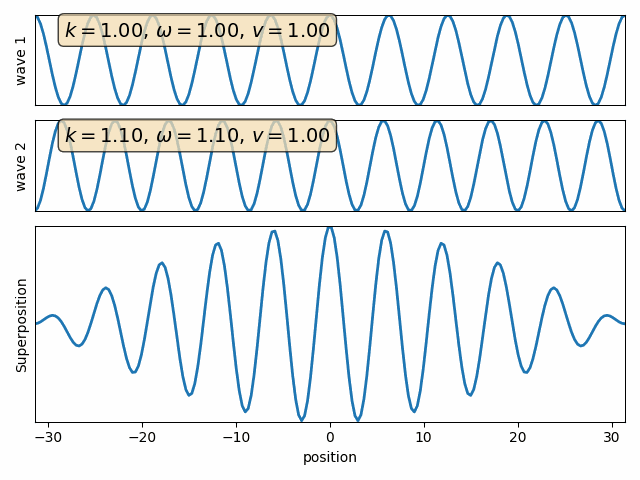
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Phase velocity and Group velocity
component
phase velocity
group velocity
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Phase velocity and Group velocity
component
phase velocity
group velocity
Intro to Quantum Mechanics - part I
Wave properties of matter and the birth of Quantum Mechanics
Wave-Particle Duality
Wave properties of matter & Intro to Quantum Mechanics
Wave-particle duality
A useful metaphor


Full moon
Crescent
The difference between these two phenomena is the setup of the observation (in this case, the position of the observer relative to the Sun-Moon direction.)
Wave properties of matter & Intro to Quantum Mechanics
Wave-particle duality
Representing particles as wave packets

Wave properties of matter & Intro to Quantum Mechanics
Wave-particle duality
Group velocity & Particle velocity
Note that if the wave packet is describing a particle, then the group velocity is equivalent to
For a free non-relativistic particle
&
i.e.
then
Implying that the group velocity gives the correct particle velocity
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave-particle duality
localization of wave packets
Recall
carrier frequency
envelope

To localize the particle at any point in time, say within two adjacent points where the envelope is 0
In other words
Or, in terms of momentum
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave-particle duality
Heisenberg's uncertainty relations
In general,
Heisenberg's uncertainty principle.
&

Example: free particle with definite momentum
Example: wave packet with components of varying momenta

Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Born's rule
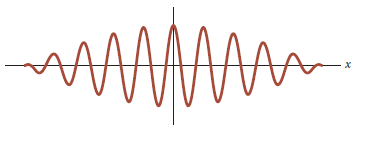
Suppose that some entity is described by a wave packet
as shown in the figure:
What is the position of this entity?
This question needs re-phrashing.
In general, Bron's rule states
&
What is the probability of finding the entity in the range ?
e.g. What is the probability that the particle is at some position
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Eg: Particle in a box
Suppose a particle with mass m is trapped inside an infinitley deep box of width L
- State the boundary conditions for the allowed wave functions.
- Determine the allowed (harmonic) wave functions.
- Determine the energies of the allowed (harmonic) wave functions.
- For the nth (harmonic) wave function, what is the most likely position to find the particle?

Since the particle is forbidden to be outside the box, the continuity of the wave function implies that it has to vanish at the boundary (box-walls):
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Eg: Particle in a box
The harmonic wave functions can be expressed as
Satisfying the boundary conditions
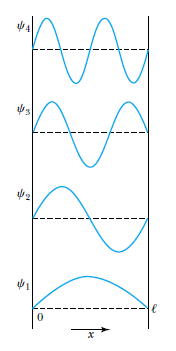
Therefore
Suppose a particle with mass m is trapped inside an infinitley deep box of width L
- State the boundary conditions for the allowed wave functions.
- Determine the allowed (harmonic) wave functions.
- Determine the energies of the allowed (harmonic) wave functions.
- For the nth (harmonic) wave function, what is the most likely position to find the particle?
How do we determine A?
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Eg: Particle in a box

Suppose a particle with mass m is trapped inside an infinitley deep box of width L
- State the boundary conditions for the allowed wave functions.
- Determine the allowed (harmonic) wave functions.
- Determine the energies of the allowed (harmonic) wave functions.
- For the nth (harmonic) wave function, what is the most likely position to find the particle?
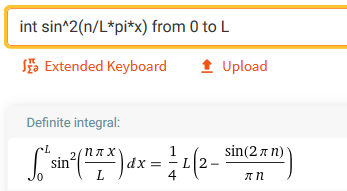
The normalization condition
i.e.
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Eg: Particle in a box
Suppose a particle with mass m is trapped inside an infinitley deep box of width L
- State the boundary conditions for the allowed wave functions.
- Determine the allowed (harmonic) wave functions.
- Determine the energies of the allowed (harmonic) wave functions.
- For the nth (harmonic) wave function, what is the most likely position to find the particle?

Recall that satisfying the boundary conditions required:
Therefore, the momentum of the particle in these harmonic states is (via de Broglie's)
And the energies are
Note that the ground state has nonzero energy! (why not?)

Also note that the ground state energy is larger for smaller boxes!
Wave properties of matter & Intro to Quantum Mechanics
Wave properties of matter
The uncertainty principle
Wave properties of matter & Intro to Quantum Mechanics
Wave motion
Eg: Particle in a box
Suppose a particle with mass m is trapped inside an infinitley deep box of width L
- State the boundary conditions for the allowed wave functions.
- Determine the allowed (harmonic) wave functions.
- Determine the energies of the allowed (harmonic) wave functions.
- For the nth (harmonic) wave function, what is the most likely position to find the particle?
Recall that the harmonic wave functions have the form
Therefore, the probability density as function of position is given by
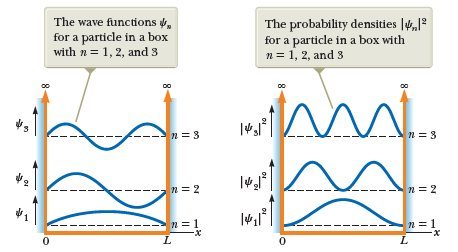
Which is maximized at
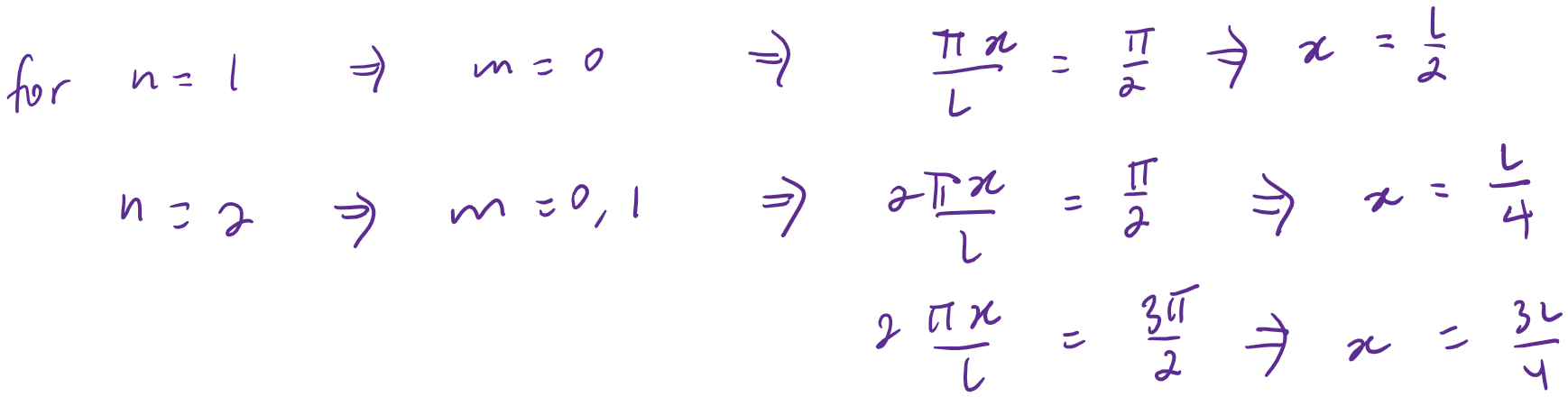
&