Temperature & Thermodynamics

  Thermodynamics is the study of general properties of macroscopic physical systems in states of thermal equilibrium, and the transformation between such states.

To start with, we would like to

  • Define Temperature and describe it qualitatively
  • Define Thermal equilibrium
  • State the zeroth law of thermodynamics
  • Get familiar with common thermometers and temperature scales
  • Understand the law of thermal expansion

Thermodynamics

    Temperature

        Objectives

How is temperature defined?

  • Operationally: Temperature is what you measure with a thermometer!

Thermodynamics

    Temperature

        Definition

What is a thermometer?

  • It's an instrument that exploits some specific thermometric property to measure temperature to a calibrated temperature scale.

A Thermometric Property is ...

  • a physical property that varies with temperature.

Thermodynamics

    Temperature

        Thermometric properties

Examples of thermometric properties:

  • The volume of a gas or liquid under constant pressure.
  • The pressure of a constant volume of gas.
  • The electrical resistance of a conductor.
  • The color of black-body radiation.
  • Thermoelectric effect.
  • ...

Liquid in Glass

Thermometer

Thermodynamics

    Temperature

        Examples of thermometers

Non-contact

Thermometer

Thermodynamics

    Temperature

        Examples of thermometers

Constant-Volume Gas Thermometer

Thermodynamics

    Temperature

        Examples of thermometers

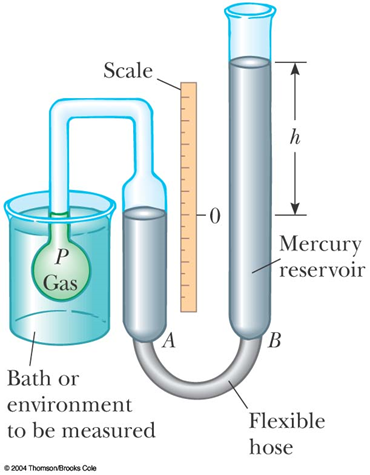
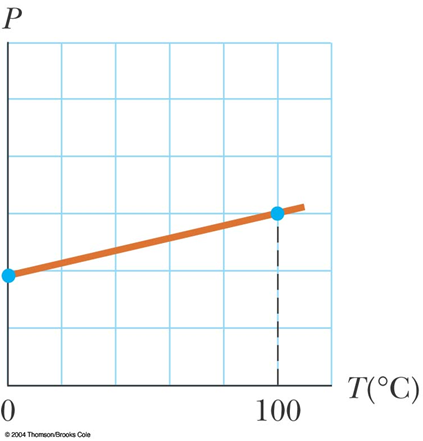
The Pressure

(of a constant-volume of gas)

varies linearly

with Temperature.

Bi-metallic strip

Thermodynamics

    Temperature

        Examples of thermometers

Thermocouples

Thermodynamics

    Temperature

        Examples of thermometers

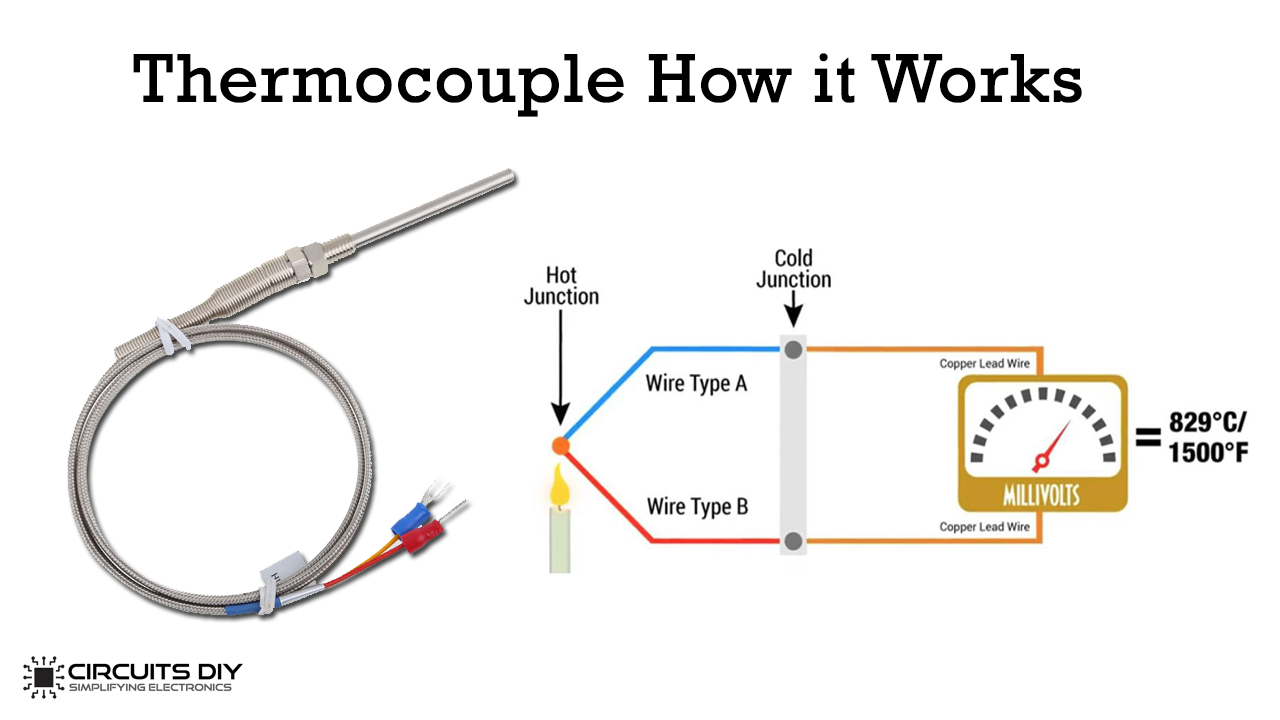
Others

Thermodynamics

    Temperature

        Examples of thermometers

 Common Temperature Scales

Thermodynamics

    Temperature

        Temperature scales

Common Temperature Scales

Thermodynamics

    Temperature

        Temperature scales

Fahernheit

Common Temperature Scales

Thermodynamics

    Temperature

        Temperature scales

Celsius

Common Temperature Scales

Thermodynamics

    Temperature

        Temperature scales

Kelvin

Common Temperature Scales

Thermodynamics

    Temperature

        Temperature scales

Rankine

Thermodynamics

    Temperature

        Converting between scales

Thermodynamics

    Temperature

        Converting between scales

Thermodynamics

    Temperature

        Converting between scales

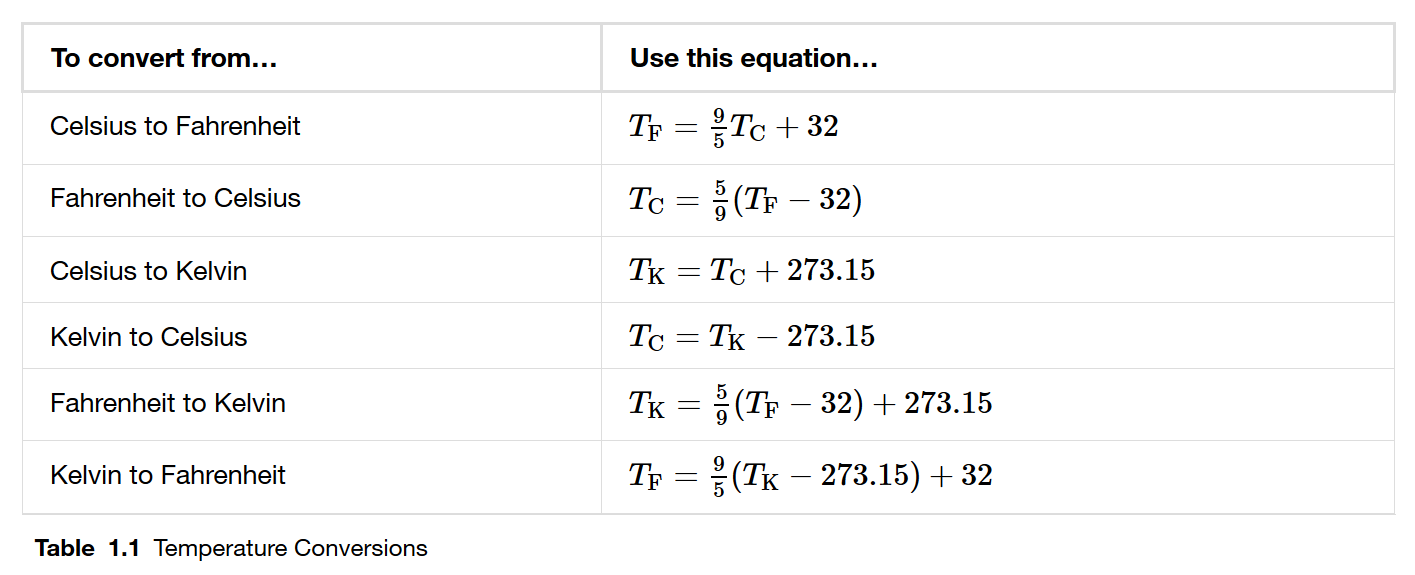
Thermodynamics

    Temperature

        [activity] Converting between scales

Thermodynamics

    Temperature

        The Kelvin scale

Make up your own scale:

Thermodynamics

    Temperature

        Temperature scales

I want to make up my own scale for temperature, which I will call the M-scale.

I want to use my own body temperature (37 C) as the zero for the M-scale; and since I do not like the heat very much, anything that is cooler than me is positive on the M-scale, and anything that is hotter than me is negative. I am most comfortable at 20 C, so I'm going to call that a 10 on the M-scale.

Find the equations that convert from the M-scale to the K-scale and vice versa.

Thermodynamics

    Temperature

        The scale of temperatures in the universe

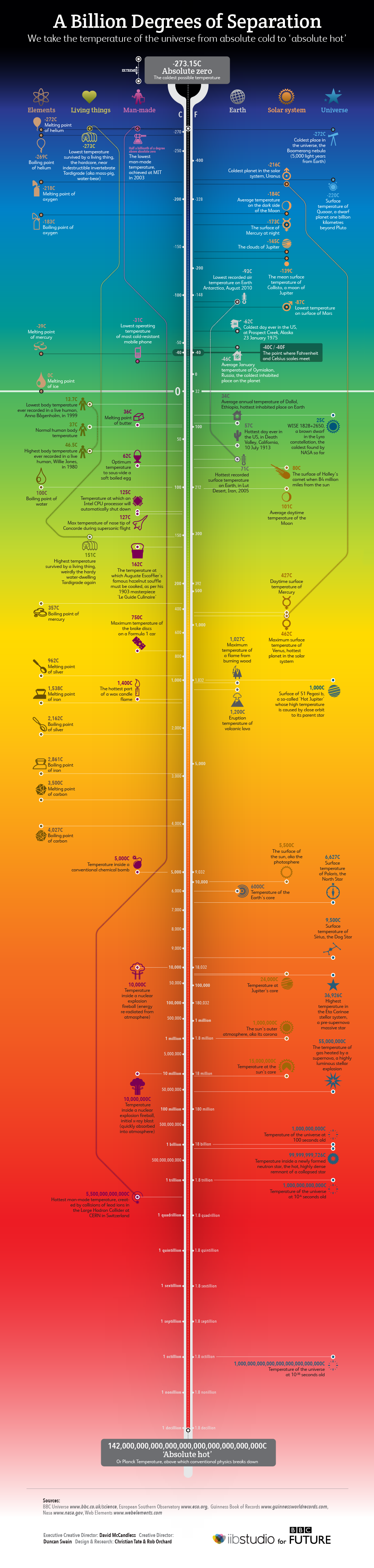
Thermodynamics

    Temperature

        The scale of temperatures in the universe

Thermodynamics

    Temperature

        A word on temperature & color

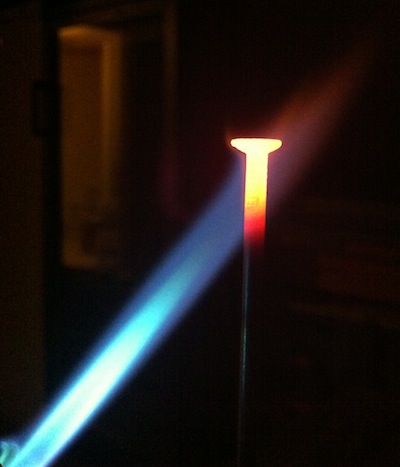
What color signifies an object at a higher temperature?

Thermodynamics

    Temperature

        Thermal Expansion

Thermodynamics

    Temperature

        Thermal Expansion

\Delta L = \alpha\ L_0\ \Delta T

Linear expansion

\Delta V = \beta\ V_0\ \Delta T

Volume expansion

Next,

  • Define Thermal Contact and Thermal Equilibrium.
  • Explain phenomena involving heat transfer.
  • Solve problems involving heat transfer.
  • Distinguish Temperature changes vs Phase changes.

Thermodynamics

    Heat Transfer

        Objectives

Thermal Contact

  • Two objects are in thermal contact with each other if energy can be exchanged between them.

 

  • The exchanges we will focus on will be in the form of heat or electromagnetic radiation (we'll get to that later).

 

  • Thermal contact does not have to also be physical contact.

 

  • Energy will be exchanged only if there is a temperature difference.

Thermodynamics

    Temperature

        Thermal contact and Thermal equilibrium

Thermodynamics

    Heat transfer

        Mechanisms of Heat Transfer

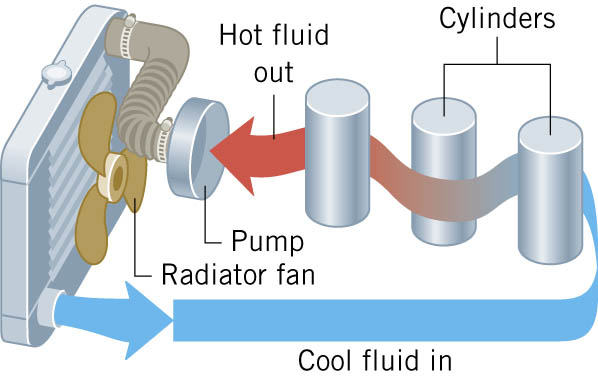
Convection

Convection is the process in which heat is carried from one place to another by the bulk movement of a fluid.

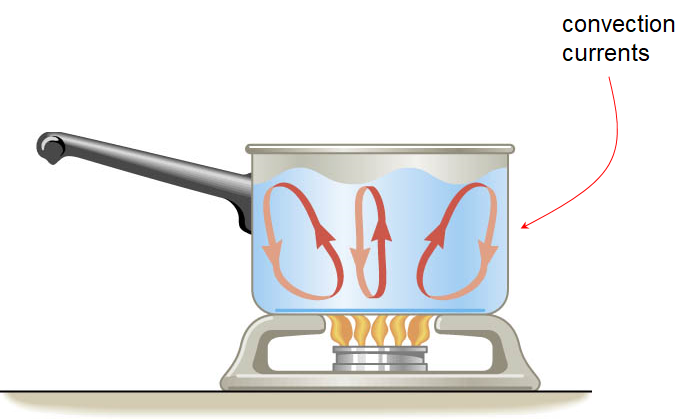
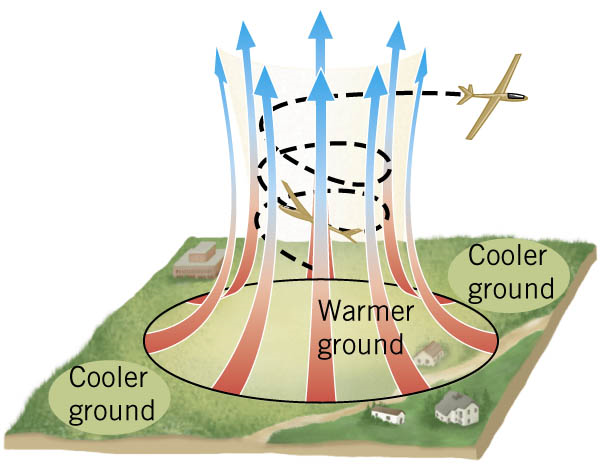
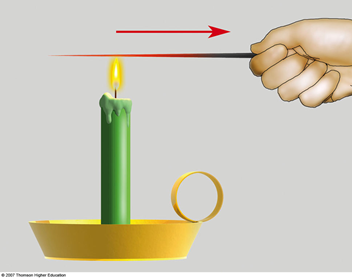
Conduction

Conduction is the process whereby heat is transferred directly through a material, with any bulk motion of the material playing no role in the

transfer.

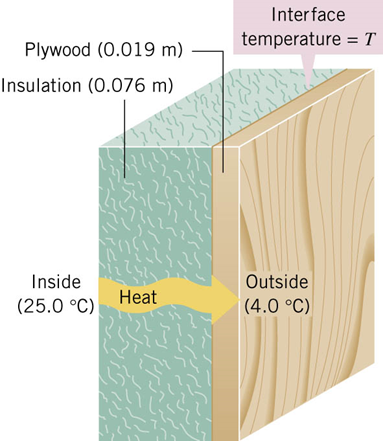
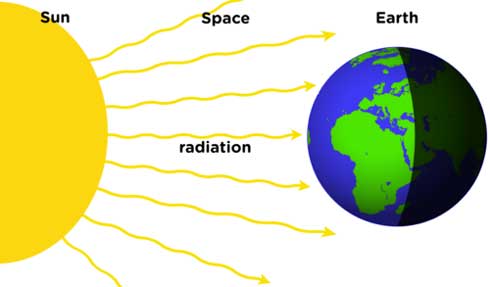
Radiation

Radiation is the process in which energy is transferred by means of electromagnetic waves.

Thermodynamics

    Heat transfer

        Mechanisms of Heat Transfer

Convection

Convection is the process in which heat is carried from one place to another by the bulk movement of a fluid.

Radiation

Radiation is the process in which energy is transferred by means of electromagnetic waves.

Conduction

Conduction is the process whereby heat is transferred directly through a material, with any bulk motion of the material playing no role in the

transfer.

Thermodynamics

    Temperature

        Thermal contact and Thermal equilibrium

Thermal Equilibrium

  • Thermal equilibrium is the state whereby objects in thermal contact do not exchange energy.

Another definition of Temperature

  • Temperature is the quantity that determines whether objects are in thermal equilibrium (i.e. whether heat energy will flow between them.)

Heat is

Thermodynamics

    Heat Transfer

        Definitions

a form of energy flow

In units of joules (or calories.)

1.000\ \text{kcal} = 4186\ \text{J}.

Internal Energy of a system

Thermodynamics

    Heat Transfer

        Definitions

sum of the mechanical energies of constituents

 is the

proportional to its temperature

andis

It is possible to change the internal energy of a system

by

transferring heat to/from the system.

 

Thermodynamics

    Heat Transfer

        Definitions

Thermodynamics

    Heat Transfer

        Heat transfer and Temperature change

+Q = m\ c\ (T_B-T_A)
-Q = m\ c\ (T_A-T_B)

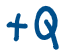
For a system of mass m and specific heat capacity c, the amount of heat transferred into or out of the system associated with a change in its temperature is given by

Q\ =\ m\ c\ \Delta T

Where the sign of the heat transferred matches the sign of the temperature change.

Thermodynamics

    Heat Transfer

        Heat transfer and Temperature change (example)

Suppose that you want to make tea with oat-milk in a ceramic mug.

 

You add 40g of cold oat-milk, which was in thermal equilibrium with the refrigerator environment at 5C; to 300g of water just below boiling point, at 94 C. You find that if the mug started at room temperature, 71.6 F, then when it equilibrates  with its contents, its temperature becomes 77.5 C

 

Take the mass of the ceramic mug to be 200g, and its specific heat capacity to be 804 J/kg K. Take the specific heat of oat milk to be 4000 J/kg K.

 

How much heat is gained/lost by each of the elements?

Example

Thermodynamics

    Heat Transfer

        Heat transfer and Temperature change (example)

mass (kg) specific heat J/(kg K) initial T (C) final T (C) heat (J)
water 0.3 4186 94 77.5 -20720.7
milk 0.04 4000 5 77.5 11600
mug 0.2 804 22 77.5 8924.4
Total -196.3

Suppose that you want to make tea with oat-milk in a ceramic mug.

 

You add 40g of cold oat-milk, which was in thermal equilibrium with the refrigerator environment at 5C; to 300g of water just below boiling point, at 94 C. You find that if the mug started at room temperature, 71.6 F, then when it equilibrates  with its contents, its temperature becomes 77.5 C

 

Take the mass of the ceramic mug to be 200g, and its specific heat capacity to be 804 J/kg K. Take the specific heat of oat milk to be 4000 J/kg K.

 

How much heat is gained/lost by each of the elements?

Example

Thermodynamics

    Heat transfer

        States (phases) of matter

There are many distinguishable states of matter

Typically distinguished by some order parameter

The classical states of matter are:

Solid,

Liquid,

Gas,

Plasma.

Thermodynamics

    Heat transfer

        States (phases) of matter

Thermodynamics

    Heat transfer

        States (phases) of matter

Thermodynamics

    Heat transfer

        Heat transfer and phase change

Q = m\ L

Heat energy required for a system of mass m

to change phases.

Where

L is the latent heat associated

with

that transition

for

that material

Thermodynamics

    Heat transfer

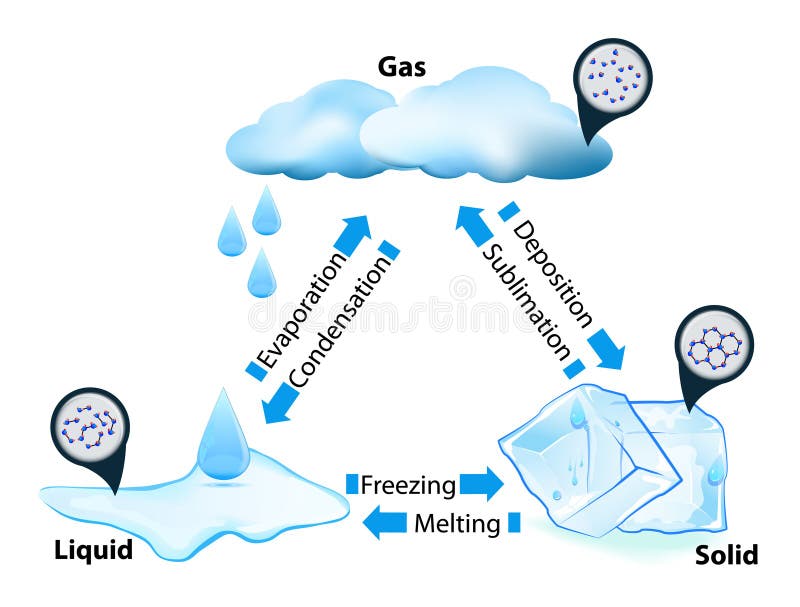
        Heat transfer and phase change (example)

How much energy does it take to turn 1.0 Ton of ice to water vapor?

btw, 1 Ton of ice, volume wise, is roughly the size of a medium washer or dryer.

Thermodynamics

    Heat transfer

        Heat transfer and phase change (example)

How much energy does it take to turn 1.0 Ton of ice to water vapor?

Sub process What is changing? Initial Temperature Final Temperature Required Heat per unit mass (J/kg) Total required Heat (J)
Ice heating up temperature -20 0 2090 /degree
Ice melting to water phase 0 0 334,000
Water heating up temperature 0 100 4186 /degree
Water vaporizing phase 100 100 2,256,000
Q_\text{total}=Q_\text{ice: -20 to 0} + Q_\text{ice to water}+Q_\text{water: 0 to 100} + Q_\text{water to steam} = 41,800,000 +334,000,000+418,600,000+2,256,000,000 = 3,050,400,000J=3\times 10^9 J
Q_\text{ice: -20 to 0} = m_\text{ice}\ c_\text{ice}\ (0-(-20)) = 1000\ \text{kg} \times 2090 \ \text{J/(kg\ K)} \times 20\ \text{K} = 41,800,000 \ \text{J}
Q_\text{ice to water} = m_\text{ice}\ L_\text{melting} = 1000 \ \text{kg} \times 334,000 \ \text{J/kg} = 334,000,000 \ \text{J}
Q_\text{water: 0 to 100} = m_\text{water}\ c_\text{water}\ (100-0) = 1000 \ \text{kg} \times 4186 \ \text{J/(kg\ K)} \times 100\ \text{K} = 418,600,000 \ \text{J}
Q_\text{water to steam} = m_\text{water}\ L_\text{vaporizing} = 1000 \ \text{kg} \times 2,256,000 \ \text{J/kg} = 2,256,000,000 \ \text{J}

btw, 1 Ton of ice, volume wise, is roughly the size of a medium washer or dryer.

Thermodynamics

    Heat transfer

        Heat transfer and phase change (example)

Example:

A 0.0500-kg ice cube at -30 C is placed in 0.400 kg of 35 C water in a very well insulated container: what is the temperature after all elements have reached thermal equilibrium?

Next,

  • Explain the macroscopic properties of gases in terms of the microscopic picture.
  • Explain and Apply the ideal gas law

Thermodynamics

    The Kinetic Theory of Gases

        Objectives

Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

How do the macroscopic properties --P, V, and T--

relate to

each other?

How do the macroscopic properties --P, V, and T--

relate to the microscopic picture?

1
2

What is an _ideal_ gas?

Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

  • A collection of molecules that are widely separated.

 

  • The interactions between the individual molecules are mostly negligible.

 

  • The motion of the molecules are independent of each other (except for the rare collision, where the momentum exchange contributes to maintaining thermal equilibrium.)

Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

How do the macroscopic properties --P, V, and T--

relate to the microscopic picture?

  • is proportional to the internal energy of the system,
  • which is the sum of the mechanical energies of the microscopic constituents. (mathematical expression coming soon.)
  • Note that temperature is not defined for a single atom or molecule.

Temperature

  • The volume of a gas is the volume of the container of the gas. 
  • The molecules of a gas fills the space it occupies.
  • Note that volume is not really defined for a single atom or molecule.

Volume

1

Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

How do the macroscopic properties --P, V, and T--

relate to the microscopic picture?

  • is a property that describes the average normal force per unit area that is exerted on any surface by the molecules of the gas.

Pressure

  • pressure is in all directions. (think Newton's 3rd)
P = \frac{F}{A}
  • the SI unit of pressure is the Pascal.
\text{Pa} = \frac{N}{m^2}
  • Atmospheric pressure
1\ \text{Atm} = 1.013 \times 10^5\ \text{Pa}
  • Gauge pressure = Absolute pressure - 1 Atm
1

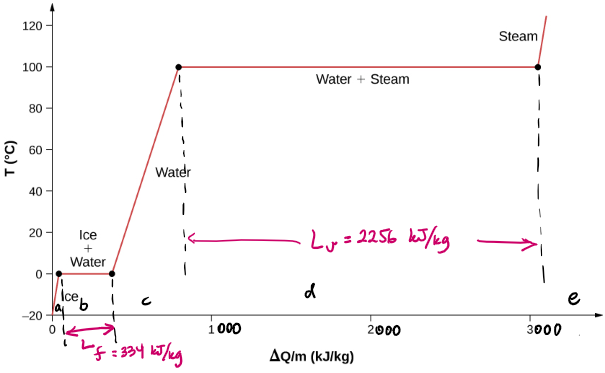
Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

Joseph Wright’s An Experiment on a Bird in the Air Pump (1768) housed at the National Gallery, London.

How do the macroscopic properties --P, V, and T--

relate to

each other?

2

Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

Boyle's Law

Constant N and T

V\ \propto\ {1}/{P}
V\ \propto\ T

Charles's Law

Constant N and P

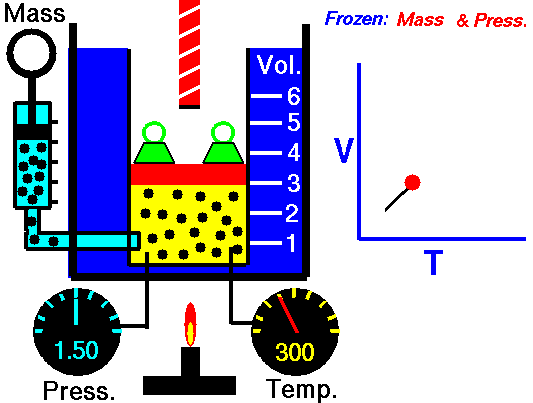
P-T Law

Constant N and V

New Experiments Physico-Mechanical, Touching the Spring of the Air and Its Effects (1660)

P\ \propto\ T

How do the macroscopic properties --P, V, and T--

relate to

each other?

2

Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

Ideal Gas Law

How do the macroscopic properties --P, V, and T--

relate to

each other?

2
P\ V\ =\ N\ k_B\ T
P\ V\ =\ n\ R\ T
n=\frac{N}{N_A}=\frac{m}{M}
R={N_A}\ {k_B}=8.314 \frac{J}{K\cdot mol}

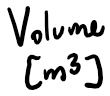
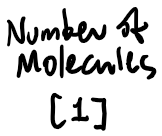
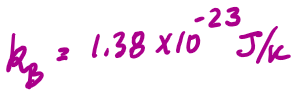
Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

Suppose 9.00g of water is vaporized inside a 2.00L container, and heated to 500 C -- what is the gauge pressure inside the container?

Example

Thermodynamics

    The Kinetic Theory of Gases

        Macroscopic properties of ideal gases

Suppose a tire is inflated to a gauge pressure of 32 Psi. If the compressed air inside the tire escapes to the outside atmosphere, what would its volume be compared to its volume inside the tire?

Example

Lastly, we would like to

  • Explain the first law of thermodynamics in terms of conservation of energy
  • Explain the second law of thermodynamics and the concept of Entropy

Thermodynamics

    The Laws of Thermodynamics

        Objectives

First, a word about work

  • Technically, Work is done by a _force_

Thermodynamics

    The Laws of Thermodynamics

        Work done by a thermodynamic system

W_{1\rightarrow 2}=\int_1^2 \vec{F}\cdot d\vec{s}
  • Work happens as the system transitions from one state to another.
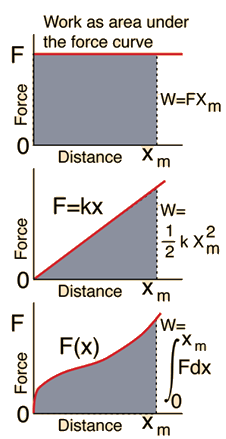
  • The work done by the force F as the system displaces along a prescribed path s from state 1 to state 2 is given by the integral along the path:

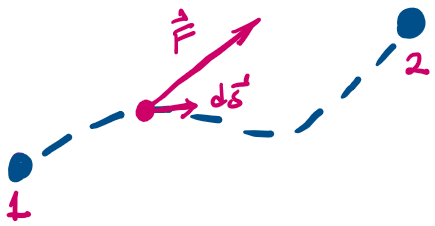
Notes

  • The work can be represented by the area "under" the force v. displacement curve.

Work done "by" a "thermodynamic system" as it expands from V_1 to V_2

Thermodynamics

    The Laws of Thermodynamics

        Work done by a thermodynamic system

W_{1\rightarrow 2}=\int_1^2 \vec{F}\cdot d\vec{s}
=\int_{x_1}^{x_2} F \ dx
=\int_{x_1}^{x_2} P\ A \ dx
\ W_{V_1\rightarrow V_2}=\int_{V_1}^{V_2} P\ dV \

Work done "by" a "thermodynamic system" as it expands from V_1 to V_2

Thermodynamics

    The Laws of Thermodynamics

        Work done by a thermodynamic system

\ W_{V_1\rightarrow V_2}=\int_{V_1}^{V_2} P\ dV \

Does the work depend on the path?

(Analysis on next slide)

              Let's classify some common processes

(but, first)

Isochoric

A\rightarrow D
B\rightarrow C

Constant Volume

Isobaric

A\rightarrow B
D\rightarrow C

Constant Pressure

Isothermal

A\rightarrow C
P_1V_1=P_2V_2

Constant Temperature

Adiabatic

No heat transfer

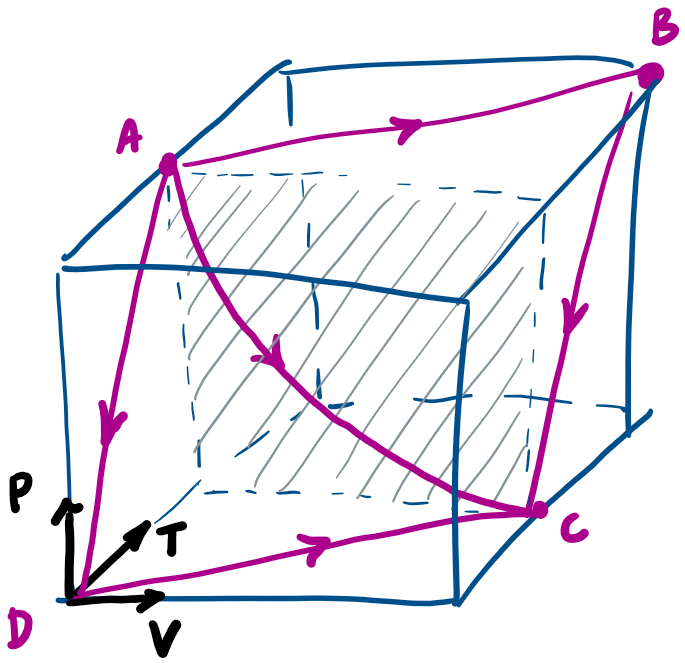
Work done "by" a "thermodynamic system" as it expands from V_1 to V_2

Thermodynamics

    The Laws of Thermodynamics

        Work done by a thermodynamic system

\ W_{V_1\rightarrow V_2}=\int_{V_1}^{V_2} P\ dV \
W_{A\rightarrow C}=W_{A\rightarrow B}+ W_{B\rightarrow C}
=\int_{V_1}^{V_2} P_1\ dV +\int_{V_2}^{V_2} P\ dV \
=P_1 \int_{V_1}^{V_2} dV +0
=P_1 (V_2-V_1)
W_{A\rightarrow C}=W_{A\rightarrow D}+ W_{D\rightarrow C}
=\int_{V_1}^{V_1} P\ dV +\int_{V_1}^{V_2} P_2\ dV \
=0+P_2 \int_{V_1}^{V_2} dV
=P_2 (V_2-V_1)
W_{A\rightarrow C}=\int_{V_1}^{V_2} P\ dV
=\int_{V_1}^{V_2} \frac{N k_B T}{V}\ dV
=N\ k_B\ T\ \int_{V_1}^{V_2} \frac{dV}{V}
=N\ k_B\ T\ \text{ln}\frac{V_2}{V_1}

Thermodynamics

    The Laws of Thermodynamics

        Temperature as a measure of internal energy

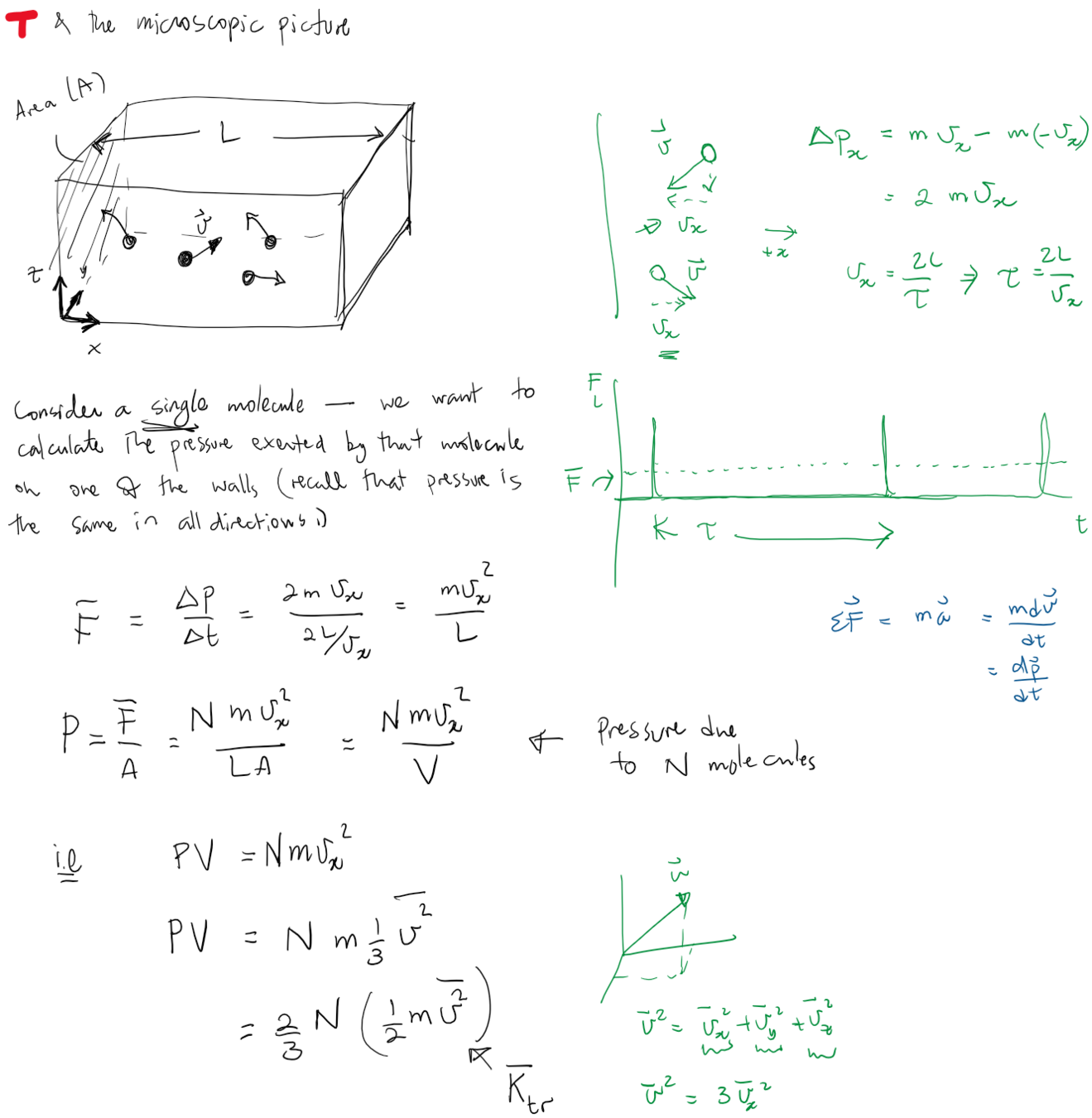
Consider an ideal gas of molecules in some thermodynamic state (P, V, T)

We wish to write an expression of the pressure exerted on the left wall by a single molecule undergoing elastic collisions with the walls.

P=\frac{\bar{F}_\perp}{A}
=\frac{\bar{J}_\text{wall on molecule}}{\Delta t \quad A}

The impulse is given by the change in momentum,

\vec{J}=\Delta \vec{p} = mv_x - (-mv_x)
= 2mv_x

And the time between successive contacts is given by:

\tau=\frac{2L}{v_x}
P=\frac{2mv_x}{2L/v_x \ A}=\frac{mv_x^2}{LA}

putting it together

P=\frac{2mv_x}{2L/v_x \ A}=\frac{mv_x^2}{LA}

Thermodynamics

    The Laws of Thermodynamics

        Temperature as a measure of internal energy

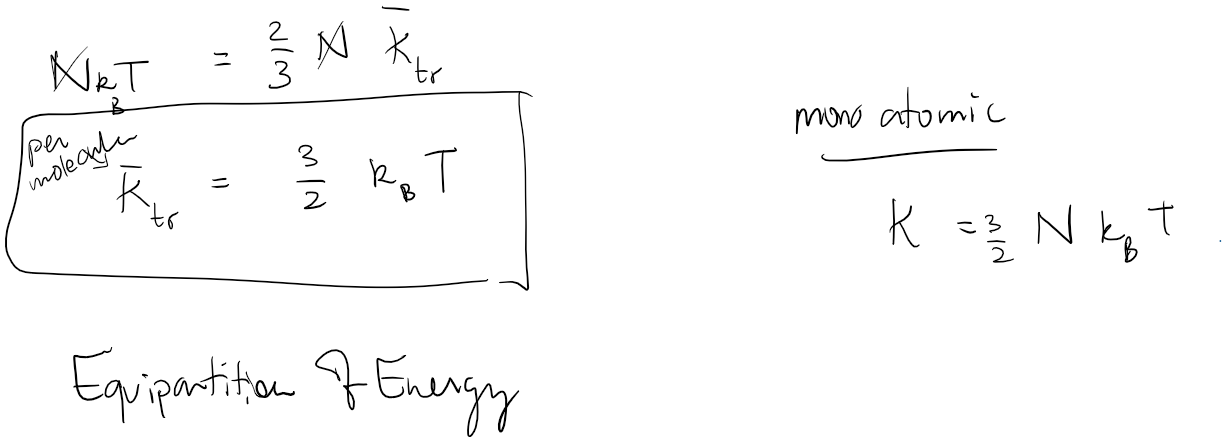
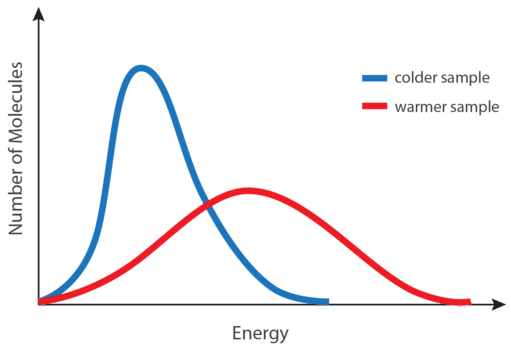
Thermodynamics

    The Laws of Thermodynamics

        First Law of Thermodynamics

Ling .... (3.7)

\Delta E_\text{int}=Q-W

Thornton .. (1.8)

\Delta U=Q+W

Essentially, 1st law is a statement about the conservation of Energy

For any transition between states of thermal equilibrium

Heat transferred

_to_

the system

The change in the internal energy of a system

 Work done _by_

the

system

?

Thermodynamics

    The Laws of Thermodynamics

        First Law of Thermodynamics

\Delta E_\text{int}=Q-W

Heat transferred

_to_

the system

The change in the internal energy of a system

 Work done _by_

the

system

process
\Delta E_\text{int}
Q
W
A \rightarrow B
B \rightarrow C
C \rightarrow D
D \rightarrow A
A \rightarrow C
C \rightarrow A

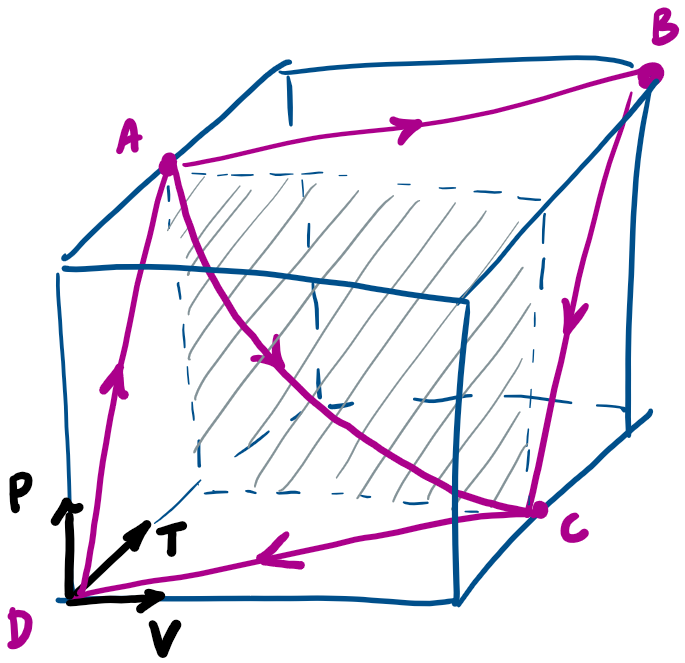
Thermodynamics

    The Laws of Thermodynamics

        First Law of Thermodynamics

\Delta E_\text{int}=Q-W

Heat transferred

_to_

the system

The change in the internal energy of a system

 Work done _by_

the

system

process
\Delta E_\text{int}
Q
W
A \rightarrow B
B \rightarrow C
C \rightarrow D
D \rightarrow A
A \rightarrow C
isobaric isochoric isobaric isochoric isotherm
+ - - + 0
+ - - + +
+ 0 - 0 +
C \rightarrow A
isobaric isochoric isobaric isochoric isotherm isotherm
+ - - + 0 0
+ - - + + -
+ 0 - 0 + -

Thermodynamics

    The Laws of Thermodynamics

        motivating 2nd law: Apparent symmetry of heat and work

\Delta E_\text{int}=Q-W

Heat transferred

_to_

the system

The change in the internal energy of a system

 Work done _by_

the

system

Q: Suppose I look at the class of all thermodynamic processes (or combinations thereof) such that the final temperature is the same as the initial temperature...

Does that mean that I can change all heat to work and all work to heat?

\Delta T=0\quad \implies\quad \Delta E_\text{int}=0\quad \implies\quad Q=W

Thermodynamics

    The Laws of Thermodynamics

        motivating 2nd law: The direction of heat flow

same action

opposite outcomes

Blowing

warms

cold hands

Blowing

cools

hot drinks

The implication is that there is a natural direction for thermodynamic evolution!

Thermodynamics

    The Laws of Thermodynamics

        motivating 2nd law: Reversibility

Q: Is it possible to reverse a thermodynamic process?

Q: What does it mean to reverse a process?

Examples from newtonian mechanics to illustrate the difference between reversible and irreversible processes:

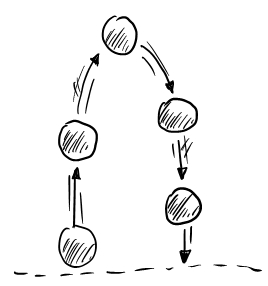
Thermodynamics

    The Laws of Thermodynamics

        motivating 2nd law: spelling it out

Suppose a block is sitting on a table, in thermal equilibrium with the surroundings.

The work you do on the system is converted into internal energy of the system and the block-table system becomes warmer → the system is no longer in thermal equilibrium with its surroundings → the system will transfer energy as heat to its surroundings until it returns to the thermal equilibrium

Suppose you spend two minutes pushing the block along the tabletop in a closed path, finally leaving the block in its initial position.

Because the final and initial states of the system are the same, the 1-st Law of TD dictates that the energy transferred to the environment as heat equals to the work done on the system.

The reverse process never occurs – a block and table that are warm will never spontaneously cool by converting their internal energy into the work that causes the block to push your hand around the table!  

Thermodynamics

    The Laws of Thermodynamics

        motivating 2nd law: spelling it out

There is a lack of symmetry in the roles played by heat and work that is not evident from the first law. This lack of symmetry is related to the fact that some processes are naturally irreversible.

Thermodynamics

    The Laws of Thermodynamics

        Statements of the second law

Thermodynamics

    The Laws of Thermodynamics

        Heat Engines

Made with Slides.com