Lukusuora

Lukusuora on esimerkki yksiulotteisesta koordinaatistosta. 

-4
−4
-\dfrac{1}{2}
−​2​​1​​
\pi
π

Jokaista lukusuoran pistettä vastaa tietty reaaliluku ja jokaista reaalilukua vastaa tietty lukusuoran piste.

Itseisarvo

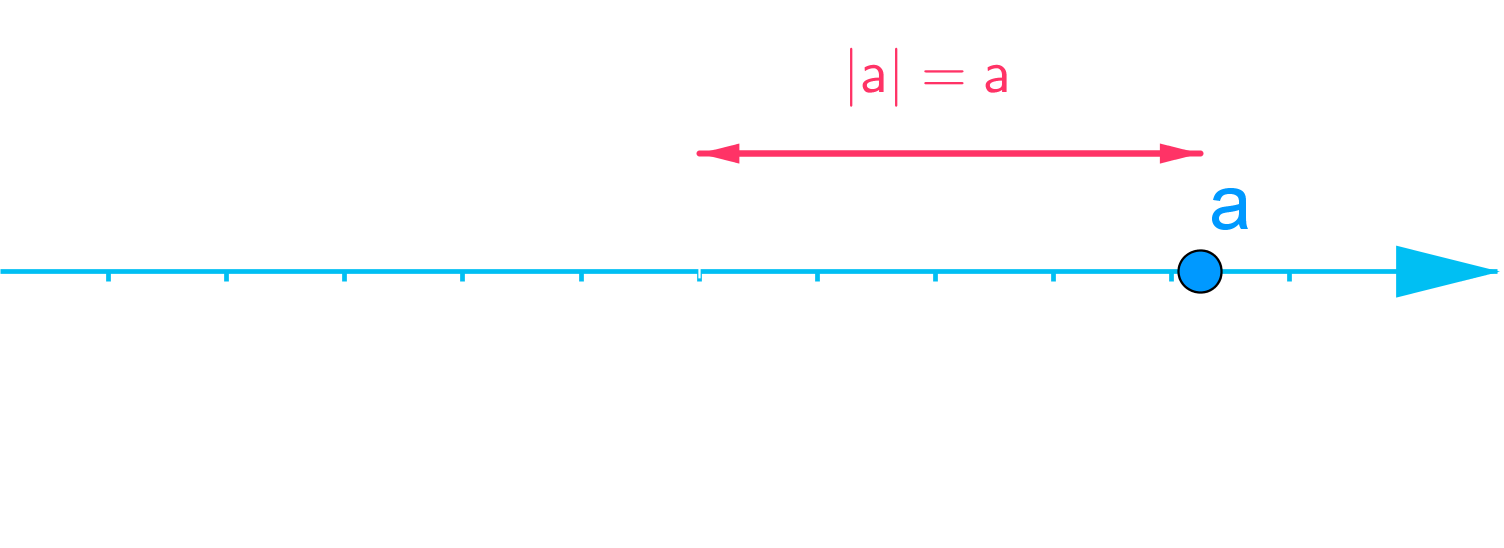
Luvun itseisarvo on luvun etäisyys luvusta nolla lukusuoralla.

Luvun a itseisarvo merkitään | a |.

4

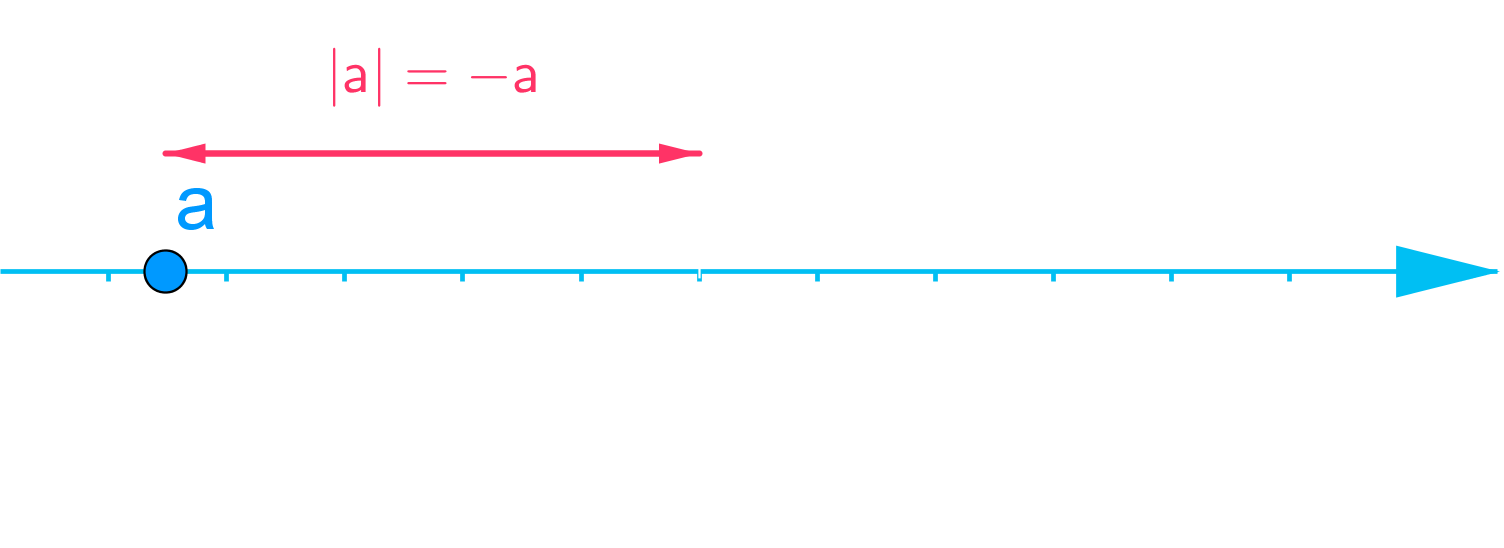
Luvun -4 itseisarvo on 4 eli 

|-4|=4
∣−4∣=4
-4
−4
\pi
π

Luvun     itseisarvo on    eli 

\pi
π
\pi
π
|\pi | = \pi
∣π∣=π
\pi
π

Itseisarvo

Itseisarvo

\text{Jos } a \geq 0, \text{ niin } |a| = a
Jos a≥0, niin ∣a∣=a
\text{Jos } a < 0, \text{ niin } |a| = -a
Jos a<0, niin ∣a∣=−a

Itseisarvo

Esimerkki

|2-\sqrt{2}|
∣2−√​2​​​∣
|\sqrt{2}-2|
∣√​2​​​−2∣

Määritä

ja

Ratkaisu

2 - \sqrt{2}\geq 0, \text{ joten } |2-\sqrt{2}|=2-\sqrt{2}
2−√​2​​​≥0, joten ∣2−√​2​​​∣=2−√​2​​​
\sqrt{2}-2 < 0, \text{ joten } |\sqrt{2}-2|=-(\sqrt{2}-2)
√​2​​​−2<0, joten ∣√​2​​​−2∣=−(√​2​​​−2)
|\sqrt{2}-2|=-\sqrt{2}+2
∣√​2​​​−2∣=−√​2​​​+2
|\sqrt{2}-2|=2-\sqrt{2}
∣√​2​​​−2∣=2−√​2​​​

Itseisarvon ominaisuuksia

|a|=|b|, \text{ jos ja vain jos } a=b \text{ tai } a=-b
∣a∣=∣b∣, jos ja vain jos a=b tai a=−b
|ab|=|a||b|
∣ab∣=∣a∣∣b∣
\Big|\dfrac{a}{b}\Big|=\dfrac{|a|}{|b|}
​∣​∣​∣​​​b​​a​​​∣​∣​∣​​=​∣b∣​​∣a∣​​

Itseisarvon määritelmästä saadaan seuraavat ominaisuudet.

Itseisarvojen yhtäsuuruus

Tulon ja osamäärän itseisarvo

ja

,b \neq 0
,b≠0

Lukujen etäisyys lukusuoralla

Lukujen a ja b etäisyys on erotuksen a-b itseisarvo | a-b |

Esimerkki

Määritä lukujen                                etäisyys toisistaan

5-3 \sqrt{3} \text{ ja } \ 2 +2 \sqrt{3}
5−3√​3​​​ ja  2+2√​3​​​

Ratkaisu

Lukujen etäisyys on erotuksen itseisarvo.

|(5-3 \sqrt{3})\color{Goldenrod}- ( 2 +2 \sqrt{3})|
∣(5−3√​3​​​)−(2+2√​3​​​)∣
=|5-3 \sqrt{3}\color{Goldenrod}- 2 \color{Goldenrod}-2 \sqrt{3}|
=∣5−3√​3​​​−2−2√​3​​​∣
=|3-5 \sqrt{3}|
=∣3−5√​3​​​∣
<0
<0
\text{Jos } a<0, \text{ niin } |a|=-a
Jos a<0, niin ∣a∣=−a
=\color{Goldenrod}-(3-5 \sqrt{3})
=−(3−5√​3​​​)
=\color{Goldenrod}-3\color{Goldenrod}+5 \sqrt{3}
=−3+5√​3​​​

Vastaus:

Lukujen välinen etäisyys on

5 \sqrt{3}-3
5√​3​​​−3

Esimerkki

Mitkä luvut toteuttavat yhtälön | x-10 | = 5 ?

Ratkaisu

Yhtälön toteuttavat sellaiset luvut, joiden etäisyys luvusta 10 on 5.

Lukusuoralta nähdään, että x on 5 tai 15.

Vastaus:

Ratkaisu

\text{Jos } x \geq 10, \text{ niin}
Jos x≥10, niin
|x-10|=x-10
∣x−10∣=x−10

1.

2.

|x-10|=5
∣x−10∣=5
x-10=5
x−10=5
x=15
x=15
\text{Jos } x < 10, \text{ niin}
Jos x<10, niin
|x-10|=-(x-10)=-x+10
∣x−10∣=−(x−10)=−x+10

1.

2.

|x-10|=5
∣x−10∣=5
-x+10=5
−x+10=5
-x=-5
−x=−5
x=5
x=5

Vastaus:

x=15 \text{ tai } x=5
x=15 tai x=5