Sistemas Inteligentes
Unidad 2: Lógica Difusa Tipo – I
Ing. Oscar Alonso Rosete Beas
Semana 18 Marzo Rev:1 ciclo 2021-1
oscarrosete.com
oscarrosete.com

Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com
Unidad 2
oscarrosete.com

oscarrosete.com

oscarrosete.com
Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com

oscarrosete.com
Lógica difusa vs lógica clásica
También llamada lógica clásica o booleana, esta fundamentada en la lógica aristotélica.
Solamente existen dos posibles valores de veracidad, donde la verdad (T) y la falsedad (F) pueden ser cualquier número en [0,1] tal que T+F=1.
Lógica aristotélica
Neutrosophic computing and machine learning

oscarrosete.com

oscarrosete.com
Lógica difusa vs lógica clásica
Gama de posibilidades de veracidad
No solo 2 posibles estados, permite valores intermedios para poder definir evaluaciones convencionales, valores entre 0 y 1.
¿Qué propone la lógica difusa?

oscarrosete.com

oscarrosete.com
Lógica difusa vs lógica clásica
Ejemplo
¿Qué tan mojada está la ropa?


oscarrosete.com

oscarrosete.com
Utilidad
El uso de técnicas de lógica difusa en control automático trata de imitar o emular el comportamiento consciente de un operador humano en el gobierno de procesos, sistemas o plantas alineales reales, los que difícilmente pueden ser modelados por los métodos fisicomatemáticos usuales.
Trasladar experiencia humana a computadora

oscarrosete.com

oscarrosete.com
Utilidad
Método básico: Traducir la experiencia o forma de trabajo de la persona experta en manipulación o control de una maquinaria en reglas lingüísticas que las comprenda una computadora.
Potencial propósito: Diseñar un controlador difuso que complemente o sustituya la operación manual.
Trasladar experiencia humana a computadora

oscarrosete.com

oscarrosete.com
Utilidad
La información que proviene de nuestro entorno que obtenemos a través de sentidos, aparatos de medición, etc tiene errores y la manera clásica de procesar la información para obtener conclusiones es utilizando teoría de probabilidad y estadística.
Otra alternativa es utilizar un razonamiento aproximado de la lógica difusa.
Procesar información con incertidumbre:

oscarrosete.com

oscarrosete.com
Control difuso
¿En qué difiere el control difuso al control convencional?
El enfoque tradicional desarrollado estuvo basado en problemas muy bien definidos con modelos precisos pero carecen de autonomía y la habilidad de la toma de decisiones.
La problemática es utilizarlos en entornos inciertos.
Intelligent Systems: Modeling, Optimization, and Control
By Yung C. Shin, Chengying Xu
oscarrosete.com

oscarrosete.com
No necesitamos modelo matemático, no se requiere identificar el sistema , lo cual lo hace más eficiente en términos del tiempo.
No necesitamos linealizarlo.
Facilita el diseño del controlador.
Desventajas:
Necesitamos conocer las reglas lingüísticas de control de un experto, en el control de cierta maquinaria o cierto sistema y traducir a reglas si y entonces de control
Ventajas
Control difuso
oscarrosete.com

oscarrosete.com
Cuando no conoces el modelo, tenemos 2 alternativas:
Control pid (una entrada y una salida)
Control difuso (multiples entradas y salidas)

Control difuso
¿En qué difiere el control difuso al control convencional?
oscarrosete.com

oscarrosete.com
Control difuso
Potenciales aplicaciones
oscarrosete.com

oscarrosete.com
Cambio fundamental de permitir que las afirmaciones tomen una gama de valores de veracidad entre 0 y 1
¿Qué puede cambiar en las matemáticas?
¿Qué implica el cambio de conjuntos clásicos a conjuntos difusos?
Las aplicaciones todavía se encuentran en investigación.
Fundamentos del control difuso

oscarrosete.com

oscarrosete.com
Nuestro enfoque será en la aplicación de lógica difusa para entender la teoría detrás de los controladores difusos (Mamdani, tsukamoto, Sugeno)
Las aplicaciones todavía se encuentran en investigación.
Fundamentos del control difuso

oscarrosete.com
oscarrosete.com
- Control de dosificación en las plantas de tratamiento de aguas residuales.
- Control de robots en inspección de túneles
- Posicionamiento en prensas
- Control de temperatura en máquinas de moldeo de plástico
- Climatización y automatización de edificios.
Aplicaciones específicas adicionales

oscarrosete.com

oscarrosete.com
Agenda
2.1. Introducción a la Lógica Difusa
2.2. Conjuntos difusos y funciones de membresía
2.3. Operaciones sobre conjuntos difusos
2.4. Inferencia usando Lógica Difusa
2.5. Diseño de clasificadores difusos
Unidad 2: Lógica Difusa Tipo – I
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Un conjunto es un grupo de elementos u objetos especificados de tal forma que se pueda afirmar con certeza que un objeto dado pertenece o no al conjunto. En general, para denotar a los conjuntos se usan las letras mayúsculas, y letras minúsculas para sus elementos.
Conjuntos
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Para los conjuntos y sus elementos se utilizan símbolos de pertenencia e igualdad.
Conjuntos

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Ejemplo


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Conjuntos clásicos (certeros)
Potencial criterio para diferenciar altos de bajos, quizás altura promedio.
Todos los que estén abajo del promedio serán clasificados como bajos.
Clasifique a las personas de acuerdo con su estatura en dos conjuntos


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Conjuntos difusos
Todas las personas pertenecen en cierta medida a ambos conjuntos.
Por ejemplo la persona mas alta del grupo puede tener una muy baja pertenencia de 0.1 al grupo de los bajos.
Clasifique a las personas de acuerdo con su estatura en dos conjuntos


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Universo de discurso
Todas las personas pertenecen en cierta medida a ambos conjuntos.
La totalidad de los elementos que se estan clasificando, se puede escoger esa totalidad o todo el mundo.
En este escenario representaría los números reales que representen las estaturas de las personas.
Conceptos básicos

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Función de membresía
Medida de pertenencia de un elemento al conjunto
0 significa no hay pertenencia al conjunto y 1 significa que hay mucha pertenencia
Conceptos básicos


Bajos
Altos
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Función de membresía para el conjunto de los bajos
La altura intermedia entre 1 y 2.5 es 1.75
Estaturas inferiores a 1.75 decrecen pertenencia y superiores a 1.75 incrementan pertenencia aproximándose a 1.
Conceptos básicos


oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
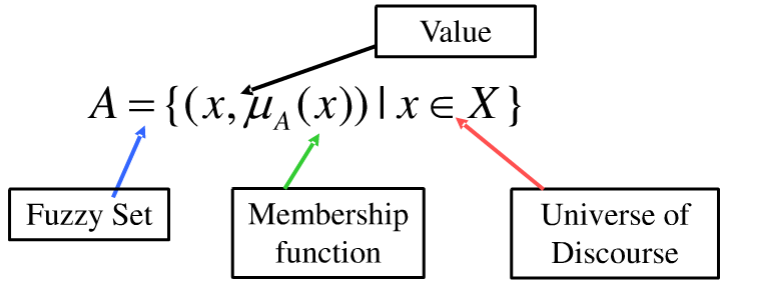
Asumamos que X es la colección de objetos representado por x, un conjunto difuso A en X es un conjunto de pares ordenados.
Entre mayor sea el valor de su funcion de membresia, mayor sera la certeza de que x pertenece a A.
Notación de los conjuntos difusos
oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Los miembros del conjunto difuso tienen un grado de pertenencia o membresía.
Un conjunto difuso puede ser representado por un conjunto de pares ordenados, el primer elemento es ensimmismo el elemento, el segundo elemento es el grado de pertenencia-membresia.
Representación pares ordenados

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Un agente de bienes raíces quiere clasificar las casas que ofrece a sus clientes. Un indicador de la comodidad de las casas es el numero de habitaciones en ellas.
Definiendo X={1,2,3,4...,10} como el conjunto de casas disponibles. El conjunto difuso de "comodidad de acuerdo al tipo de casa para una familia" puede ser descrito de la siguiente manera:
Ejemplo de estudio de conjuntos difusos

oscarrosete.com

oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Representación como la unión de sus elementos (Conjuntos difusos discretos)



Función de membresía
oscarrosete.com
oscarrosete.com
Conjuntos clásicos vs conjuntos difusos
Representación como la unión de sus elementos (Conjuntos difusos continuos)
Función de membresía



oscarrosete.com
oscarrosete.com
Conjuntos clásicos
B es un subconjunto de A, porque todos sus elementos están contenidos en A.
Si solo parcialmente algunos de B están en A, entonces B no es un subconjunto de A


oscarrosete.com
oscarrosete.com
Conjuntos difusos
El conjunto difuso B es subconjunto del conjunto difuso A si y solo si la función de membresia de B es menor o igual a la funcion de membresia de A


oscarrosete.com
oscarrosete.com
Conjuntos Certeros
La intersección sera definida como todos los elementos que estén en A y B.


oscarrosete.com
oscarrosete.com
Conjuntos Difusos
La intersección sera definida como todos los elementos que estén en A y B.




oscarrosete.com
oscarrosete.com
Conjuntos Certeros
La unión sera definida como todos los elementos que estén en A ó en B.


oscarrosete.com
oscarrosete.com
Conjuntos Difusos
La unión sera definida como todos los elementos que estén en A ó en B.

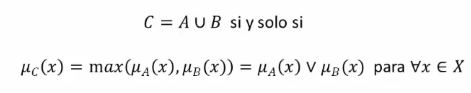


oscarrosete.com
oscarrosete.com
Conjuntos Certeros
El complemento sera definido como todos los elementos que estén en X, pero no en A