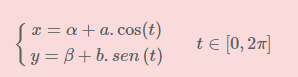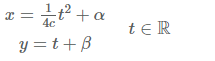Cálculo Multivariable

Unidad 1: Ecuaciones Paramétricas y coordenadas polares.

Ing. Oscar Alonso Rosete Beas

Semana 7 Septiembre Rev:2 ciclo 2020-2

 

Agenda

1.1 Introducción y encuadre del curso.
1.2 Ecuaciones paramétricas, definición y aplicación a las formas cicloidales y cónicas.
1.3 Trazado y descripción de situaciones que requieran coordenadas paramétricas, longitud de
arco.
1.4 Coordenadas polares: definición, trazado y curvas notables, cónicas.
1.5 Cálculo de áreas empleando coordenadas polares.

Unidad 1: Ecuaciones Paramétricas y coordenadas polares.

Unidad 1

Ejercicios alumnos 2

En los ejercicios, de el vector v mediante sus componentes y dibuje el vector con su punto inicial en el origen.

Ejemplo ilustrativo

Dados v=<-2,5> y w=<3,4>, encuentre cada uno de los vectores.

a. 1/2 v

b. w-v

c. v+2w

Operaciones vectoriales

Dados los siguientes vectores:

 

 

Encontrar

a) 2/3u

b) 3v

c) v-u

d) 2u+5v

Teorema vector unitario en la dirección de v

En muchas aplicaciones de los vectores es util encontrar un vector unitario que tenga la misma direccion que un vector dado. El teorema siguiente da un procedimiento para hacer esto.

 

Si v es un vector distinto de cero en el plano, entonces el vector

 

 

tiene longitud 1 y la misma dirección que v.

Normalización de v

Ejemplo ilustrativo

Halle un vector unitario en la dirección de v=<-2,5> y verifique que tiene longitud 1.

tiene longitud 1 y la misma dirección que v.

Normalización de v

Vectores unitarios canónicos o estándar

A los vectores unitarios (1,0) y (0,1) se les llama vectores unitarios canónicos o estándares en el plano y se denotan por.

 

 

Estos pueden utilizarse para representar cualquier vector de manera única, como sigue:

 

v=<v1,v2>=<v1,0>+<0,v2>=v1<1,0>+v2<0,1>=v1i+v2j

v1 y v2 son llamados componentes horizontal y vertical de v.

Ejemplo ilustrativo

Sea u el vector con punto inicial (2,-5) y punto final (-1,3), y sea v=2i-j. Exprese cada vector como combinación lineal de i y j.

 

 

 

Ejercicios alumnos

Encontrar un vector unitario, halle el vector unitario en la dirección de v y verifique que tiene longitud 1.

 

 

 

Vector en una dirección y magnitud dada

Si u es un vector unitario y theta es el angulo(medido en el sentido contrario a las manecillas del reloj) desde el eje x positivo hasta u, el punto final de u esta en el circulo unitario, y tiene:

 

Ademas cualquier vector distinto de cero v que forma un angulo con el eje x positivo tiene la misma direccion que u y puede escribir:

Ejemplo ilustrativo

El vector v tiene una magnitud de 3 y forma un angulo de 30 con el eje x positivo. Exprese v como combinacion lineal de los vectores unitarios i y j.

Ejercicios

Halle el vector v de la magnitud dada en la misma dirección que u.

Operaciones con vectores

Propiedades de las operaciones con vectores

Ejemplo ilustrativo

Un avion viaja a una altitud fija con un factor de viento despreciable y mantiene una velocidad de 500 millas por hora con un rumbo de 330. Cuando alcanza cierto punto, el avion encuentra un viento con una velocidad de 70 millas por hora en direccion 45 NE. ¿Cuáles son la velocidad y la dirección resultante del avion?

Coordenadas en el espacio

Antes de extender el concepto de vector a tres dimensiones, se debe poder identificar puntos en el sistema  de coordenadas tridimensional. Se puede construir este sistema trazando en el origen un eje z perpendicular al eje x y al eje y.

Tomado por pares, los ejes determinan tres planos coordenados: el plano xy, el plano xz y el plano yz. Estos tres planos coordenados dividen el espacio tridimensional en ocho octantes. El primer octante es en el que todas las coordenadas son positivas.

Coordenadas en el espacio

En este sistema tridimensional un punto P en el espacio está determinado por una terna ordenada (x,y,z) donde x,y y z son:

x=distancia dirigida que va del plano yz a P

y= distancia dirigida que va del plano xz a P

z=distancia dirigida que va del plano xy a P

Coordenadas en el espacio

Coordenadas en el espacio

Los puntos en el sistema de coordenadas tridimensional se representan por medio de ternas ordenadas.

Muchas de las formulas establecidas para el sistema de coordenadas bidimensional pueden extenderse a tres dimensiones. para encontrar la distancia entre dos puntos en el espacio, es usa dos veces el teorema pitagorico. 

 

Coordenadas en el espacio

La fórmula de la distancia entre los puntos (x1,y1,z1) y (x2,y2,z2)

Coordenadas en el espacio

Ejemplo ilustrativo

Encuentre la distancia entre los puntos (2,-1,3) y (1,0,-2)

Una esfera con centro en (x0,y0,z0) y radio r está definidia como el conjunto de todos los puntos tales que la distancia entre (x,y,z) y (x0,y0,z0) es r. Puede usar la formula distancia para encontrar la ecuación canónica o estándar de una esfera de radio r.

Considerando (x,y,z) como un punto arbitrario en la esfera, la ecuación:

Ecuación canónica de una esfera

El punto medio del segmento de recta que une a los puntos (x1,y1,z1) y (x2,y2,z2)

Punto medio del segmento de recta

Ejemplo ilustrativo

Determine la ecuación canónica o estándar de la esfera que tiene los puntos (5,-2,3) y (0,4,-3) como extremos de un diámetro.

Vectores en el espacio

En el espacio los vectores se denotan mediante ternas ordenadas v=<v1,v2,v3>. El vector cero se denota 0=<0,0,0>. Usando los vectores unitarios:

i=<1,0,0>, j=<0,1,0> y k=<0,0,1>

 

La notacion de vectores unitarios canónicos o estándar para v es:

v=v1i+v2j+v3k

Vectores en el espacio

Si v se representa por el segmento de recta dirigido de P(p1,p2,p3) a Q(q1,q2,q3), como se muestra en la figura, las componentes de v se obtienen restando las coordenadas del punto inicial de las coordenadas del punto final:

 

Propiedades en el espacio

Las propiedades de suma de vectores y la multiplicación  por un escalar en 2D también lo es en 3D.

Ejemplo ilustrativo

Encuentre las componentes y la longitud del vector v que tiene punto inicial (-2,3,1) y punto final (0,-4,4).

Después, halle un vector unitario en la dirección de v.

Vectores paralelos

Dos vectores distintos de cero u y v son paralelos si hay algun escalar c tal que u=cv.

El vector w tiene punto inicial (2,-1,3) y punto final (-4,7,5). cual de los siguientes vectores es paralelo a w?

u=<3,-4,-1>

v=<12,-16,4>

Vectores paralelos

Dos vectores distintos de cero u y v son paralelos si hay algun escalar c tal que u=cv.

El vector w tiene punto inicial (2,-1,3) y punto final (-4,7,5). ¿Cuál de los siguientes vectores es paralelo a w?

u=<3,-4,-1>

v=<12,-16,4>

Ejercicios alumnos

Subir la solución a la actividad correspondiente en blackboard

Gráfica manual en un mismo plano

Gráfica software en un mismo plano

Ejercicios alumnos

Encuentre las longitudes de los lados del triángulo con los vértices que se indican, y determine si el triángulo es rectángulo, isósceles o ninguna de ambas cosas.

Ejercicios alumnos

Halle la ecuación estándar de la esfera.

Puntos terminales de un diámetro: (2,0,0), (0,6,0)

Expresar un vector en el espacio en su forma de componentes.

a)Encuentre las componentes del vector v,

b)Escriba el vector utilizando la notacion del vector unitario estándar

c)Dibuje el vector con su punto inicial en el origen.

Ejemplo ilustrativo

Expresar un vector en el espacio en su forma de componentes.

a)Encuentre las componentes del vector v.

b)Escriba el vector utilizando la notacion del vector unitario estándar.

c)Dibuje el vector con su punto inicial en el origen.

e) Encontrar vector unitario en dirección.

f) Encontrar vector unitario longitud 7.

Ejemplos adicionales

Determine si los puntos

P(1,-2,-3)

Q(2,1,0)

R(4,7,-6)

son colineales

Ejemplos adicionales

Notación empleando los vectores unitarios canónicos.

 

Encuentre el punto final del vector v=7i-j+3k, dado que el punto inicial es P(-2,3,5).

Timer

Agenda

1.1 Introducción y encuadre del curso.
1.2 Ecuaciones paramétricas, definición y aplicación a las formas cicloidales y cónicas.
1.3 Trazado y descripción de situaciones que requieran coordenadas paramétricas, longitud de arco.
1.4 Coordenadas polares: definición, trazado y curvas notables, cónicas.
1.5 Cálculo de áreas empleando coordenadas polares.

Unidad 1: Ecuaciones Paramétricas y coordenadas polares.

30/08

Gráfica Ecuaciones paramétricas

Traza la curva dada por las ecuaciones paramétricas. Donde

 

30/08

Gráfica Ecuaciones paramétricas software

30/08

Gráfica Ecuaciones paramétricas

Al hecho de encontrar la ecuación rectangular que representa la gráfica de un conjunto de ecuaciones paramétricas se le llama eliminación del parámetro.

Se puede eliminar como sigue:

30/08

Hallar Ecuaciones paramétricas

Si sabemos que la gráfica de 2 ecuaciones paramétricas puede ser similar.

¿Cómo determinar un conjunto de ecuaciones paramétricas para una gráfica o una descripción física dada?

a)t=x

b) La pendiente m= dy/dx en el punto (x,y)

30/08

Ecuaciones paramétricas

En una presentación realizada en equipos

1. Definir 2 aplicaciones de las ecuaciones paramétricas en la ingeniería. Proponer un ejercicio con datos conocidos de una situación real relacionado a la aplicación mencionada que pueda apoyarse con la utilización de ecuaciones paramétricas.
2. Graficar la ecuación paramétrica.
3. Obtener la ecuación rectangular.

 

Ejercicios individual

30/08

Toda sección cónica o simplemente cónica puede describirse como la intersección de un plano y un cono de dos hojas.

30/08

Cónicas

30/08

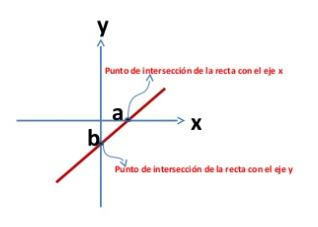
Recta

Ecuación canónica o estándar de una circunferencia

30/08

Circunferencia

30/08

Ecuaciones paramétricas de una circunferencia

La elipse es el lugar geométrico de todos los puntos de un plano, tales que la suma de las distancias a otros dos puntos fijos, llamados focos, es constante.

30/08

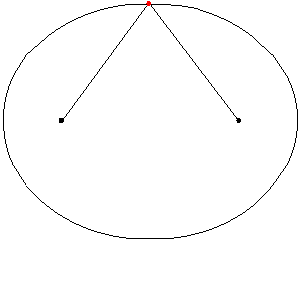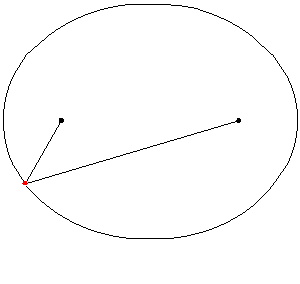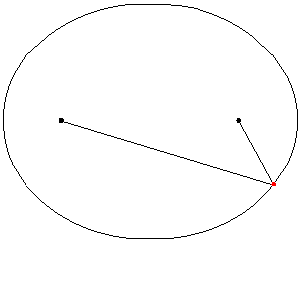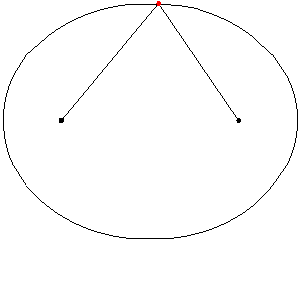
Elipse

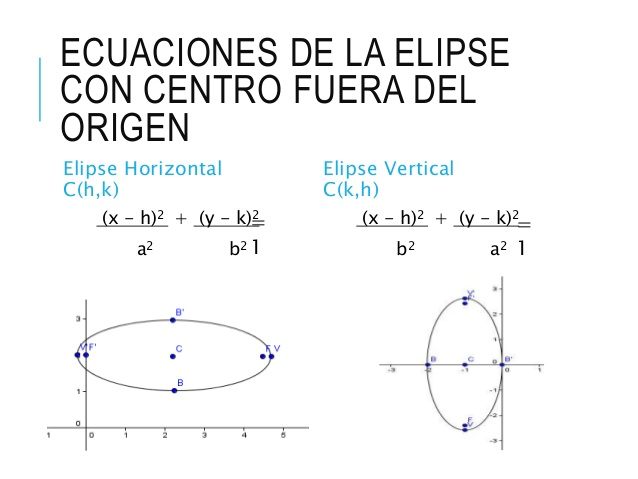
Ecuación canónica o estándar de una  elipse con centro (h,k) y longitudes de los ejes mayor y menor 2a y 2b, donde a>b, es:

30/08

Elipse

30/08

Elipse

30/08

Ecuaciones paramétricas elipse

Parametrización de la elipse con $C\left(\alpha ,\beta \right)$ y semiejes  y .

Ecuaciones paramétricas

En una presentación realizada en equipos

1. Definir 2 aplicaciones de las ecuaciones paramétricas en la ingeniería. Proponer un ejercicio con datos conocidos de una situación real relacionado a la aplicación mencionada que pueda apoyarse con la utilización de ecuaciones paramétricas.
2. Graficar la ecuación paramétrica.
3. Obtener la ecuación rectangular.

 

Ejercicios individual

02/09

Hipérbola

02/09

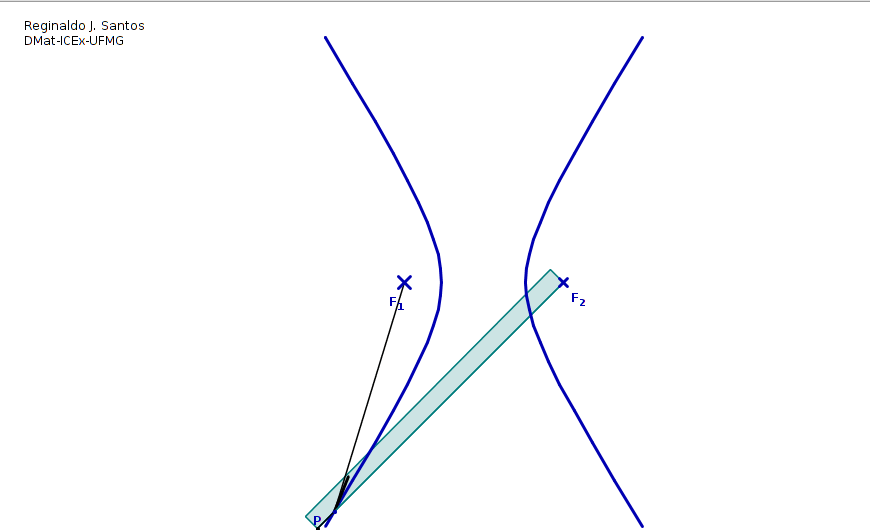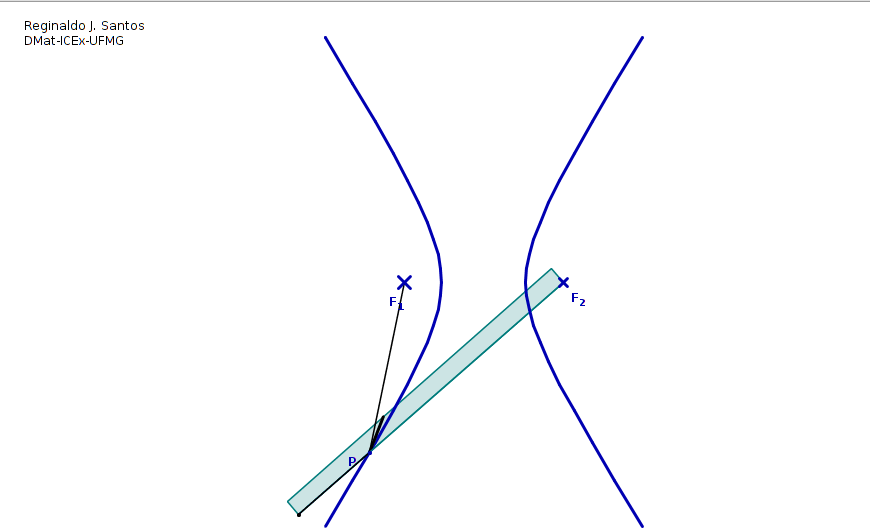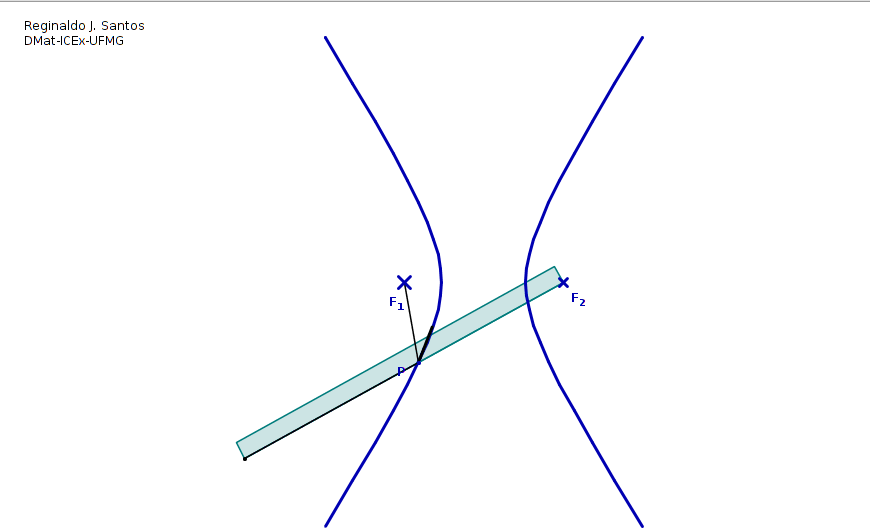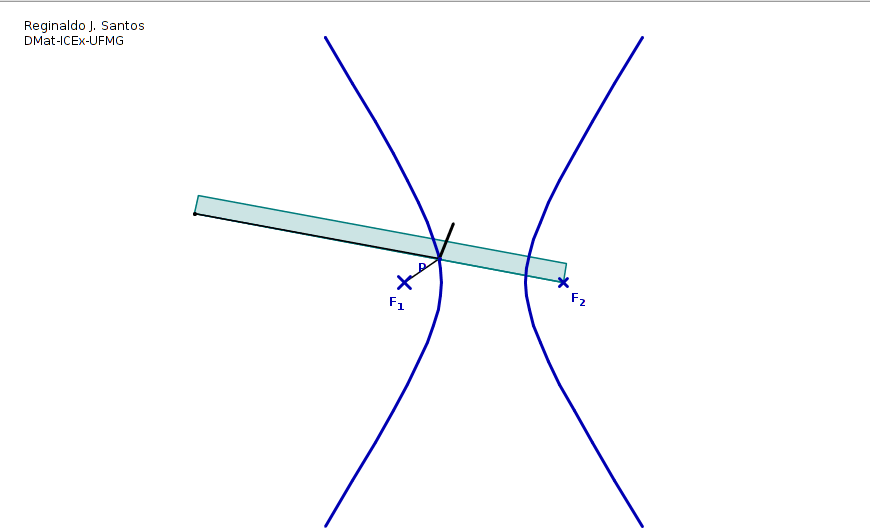
Una hipérbola es el conjunto de todos los puntos (x,y) para los que el valor absoluto de la diferencia entre las distancias a dos puntos fijos llamados focos es constante.

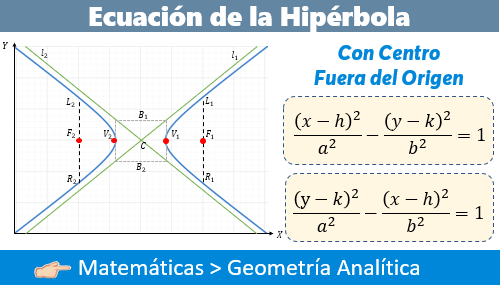
Ecuaciones canónicas hipérbola

02/09

Eje focal horizontal

Eje focal vertical

Ecuaciones paramétricas hipérbola

02/09

Parametrización de la hipérbola con centro C(0,0) y eje focal y =0 (eje x)

 

02/09

Parametrización de la hipérbola con centro C(0,0) y eje focal x =0 (eje y)

 

Ecuaciones paramétricas hipérbola

Agenda

1.1 Introducción y encuadre del curso.
1.2 Ecuaciones paramétricas, definición y aplicación a las formas cicloidales y cónicas.
1.3 Trazado y descripción de situaciones que requieran coordenadas paramétricas, longitud de arco.
1.4 Coordenadas polares: definición, trazado y curvas notables, cónicas.
1.5 Cálculo de áreas empleando coordenadas polares.

Unidad 1: Ecuaciones Paramétricas y coordenadas polares.

06/09

Parábola

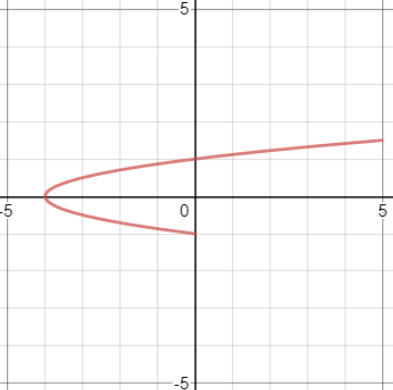
La parábola es el conjunto de todos los puntos (x,y) equidistantes de una recta fija llamada directriz y de un punto fijo, fuera de dicha recta, llamada foco. El punto medio entre el foco y la directriz es el vértice, y la recta que pasa por el foco y el vertice es el eje de la parábola.

06/09

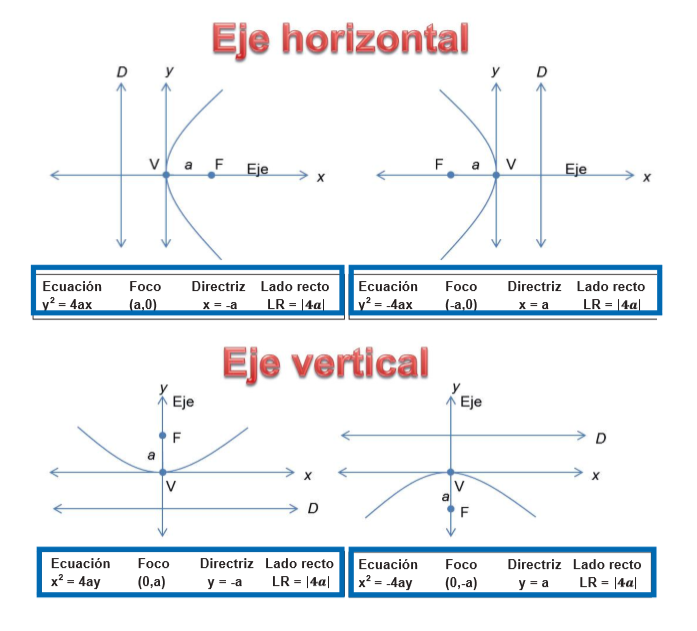
La forma estándar o canónica de la ecuación de una parábola con vértice (h,k) y directriz y=k-p (eje vertical) es

 

 

Para la directriz x=h-p (eje horizontal) la ecuacion es

 

Las coordenadas del foco son para eje horizontal y eje vertical las siguientes:

Parábola

06/09

Parábola

06/09

Ecuaciones paramétricas parábola

En el caso en que la parábola sea de eje focal vertical, resulta:

06/09

Longitud de arco de ecuación paramétrica

• Imagina aproximar la curva con un montón de pequeños segmentos de recta.

• La longitud de cada segmento está dada por el teorema de Pitágoras.

• Los términos $dx$,  y $dy$, y representan el pequeño cambio en los valores de $x$ y $y$desde el principio hasta el final del segmento.

06/09

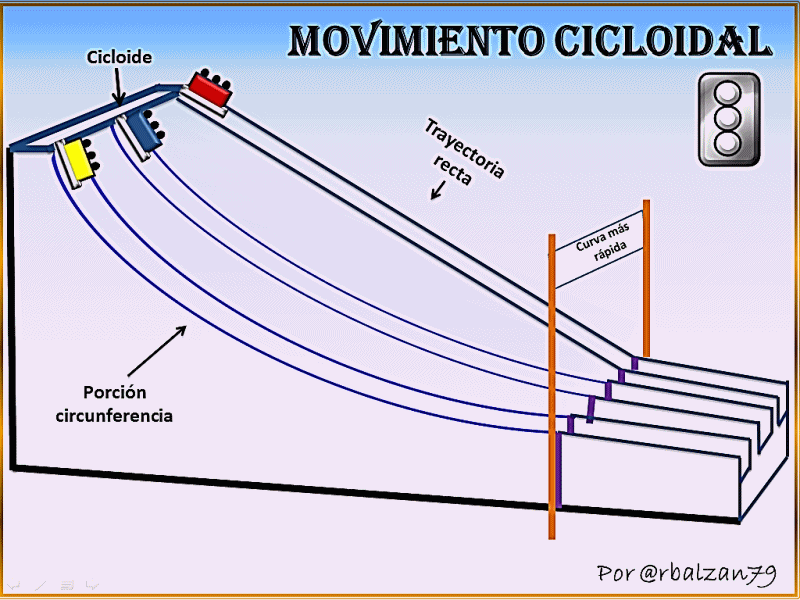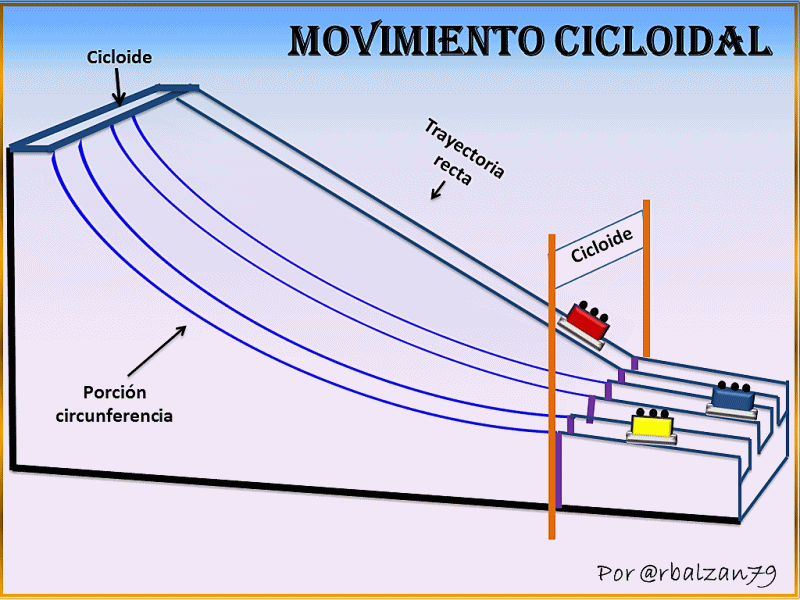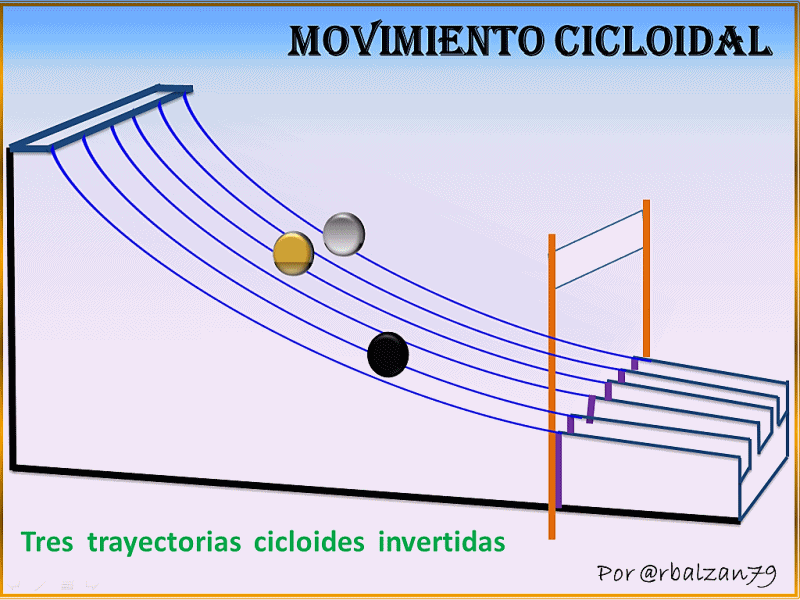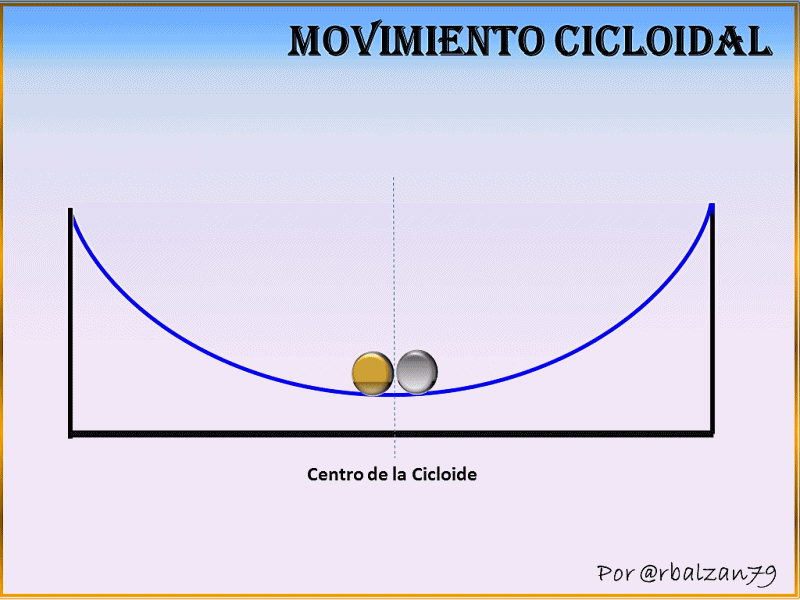
Galileo fue el primero en llamar la atencion hacia la cicloide, recomendando que se empleara en los arcos de los puentes.

La cicloide tiene tantas propiedades interesantes y ha generado disputas entre los matematicos "la Helena de la geometria"

06/09

Cicloides

Aplicaciones Cicloides

06/09

06/09

Cicloides

La condición de rodadura, que se cumple cuando un sólido se desplaza por una superficie rodando y sin deslizar.

Por ejemplo, si tenemos una rueda que gira cumpliendo la condición de rodadura, tendremos que tras un giro completo la distancia recorrida habrá sido exactamente la longitud de su circunferencia. 

06/09

Cicloides

Ecuaciones paramétricas de Cicloides

06/09

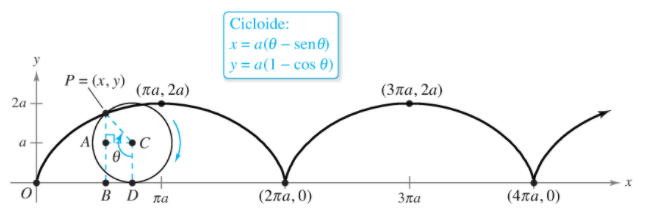
Sea x el parámetro que mide la rotación del circulo y suponemos el inicio P=(x,y) en el origen.

Cuando theta=0, P se encuentra en el orgien.

Cuando theta=π, P está en un punto maximo(πa,2a). cuando theta=2π, p vuelve al eje x en (2πa,0)

06/09

Ecuaciones paramétricas de Cicloides

Agenda

1.1 Introducción y encuadre del curso.
1.2 Ecuaciones paramétricas, definición y aplicación a las formas cicloidales y cónicas.
1.3 Trazado y descripción de situaciones que requieran coordenadas paramétricas, longitud de arco.
1.4 Coordenadas polares: definición, trazado y curvas notables, cónicas.
1.5 Cálculo de áreas empleando coordenadas polares.

Unidad 1: Ecuaciones Paramétricas y coordenadas polares.

10/09

Coordenadas cartesianas

Un sistema coordenado representa un punto en el plano mediante un par ordenado de números llamados coordenadas. Por lo general usamos coordenadas cartesianas, que son las distancias dirigidas desde dos ejes perpendiculares.

10/09

Coordenadas polares

Sistema coordenado introducido por Newton, que es más conveniente para muchos propósitos.

Se elige un punto en el plano que se llama polo (u origen) y se identifica con O. Luego se dibuja un rayo (semirrecta) que empieza en O llamado eje polar. Usualmente, este eje se traza horizontalmente a la derecha, y corresponde al eje x positivo en coordenadas cartesianas.

10/09

Coordenadas polares

Si P es cualquier otro punto en el plano, sea r la distancia de 0 a P y sea θ el ángulo (por lo regular medido en radianes) entre el eje polar y la recta OP como en la figura. Entonces el punto P se representa mediante el par ordenado (r, θ) y r, θ se llaman coordenadas polares de P. Un ángulo es positivo si se mide en el sentido contrario a las manecillas del reloj desde el eje polar.

10/09

Coordenadas polares

Extendemos el significado de las coordenadas polares (r, θ) al caso en que r es negativa estando de acuerdo en que, como en la figura, los puntos (-r, θ) y (r, θ) están sobre la misma recta que pasa por 0 y a la misma distancia |r| desde 0, pero en lados opuestos de 0. Si r>0, el punto (r, θ) está en el mismo cuadrante que θ; si r<0, está en el cuadrante sobre el lado opuesto del polo. Observe que (-r,θ) representa el mismo punto que (r, θ+π ).

10/09

Coordenadas polares

10/09

(1,5π /4)

(2,3π)

(2,-2π/3)

(-3,3π/4) 

Coordenadas polares

10/09

En el sistema coordenado cartesiano todo punto tiene sólo una representación, pero en el sistema de coordenadas polares cada punto tiene muchas representaciones. Por ejemplo, el punto (1, 5π/4) se podría escribir como (1, -3π/4) o (1, 13π/4) o (1, π/4).

Coordenadas polares

10/09

De hecho, puesto que una vuelta completa en sentido contrario a las manecillas del reloj está dada por un ángulo 2π , el punto representado por coordenadas polares (r, θ) se representa también por

 

 

donde n es cualquier entero.

Coordenadas polares

10/09

La conexión entre coordenadas polares y cartesianas se puede ver en la figura , en la cual el polo corresponde al origen y el eje polar coincide con el eje x positivo. Si el punto P tiene coordenadas cartesianas (x, y) y coordenadas polares (r, θ), entonces, de la figura, se tiene

 

 

 

 

 

valido para r>0 y 0<θ<π/2

Curvas polares

10/09

Curvas polares

10/09

Simetría

10/09

Actividad estudiante

 

1. Bosqueje la curva r=1+senθ
2. Bosqueje la curva r=cos2θ
3. Encuentre la ecuación rectangular equivalente a r=2senθ

 

Comprobar con graficación por software

 

Subir en un documento a Blackboard.

 

10/09