Dinámica de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
Ing. Oscar Alonso Rosete Beas
Semana 25 Enero Rev:1 ciclo 2021-1
oscarrosete.com
oscarrosete.com

Agenda
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com
Unidad 1
oscarrosete.com

oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Horas de Clase Asistidas: 80
Horas de Clase Independientes: 80
Duración Total: 160 horas
Horario: Martes 19:00-21:00 / Jueves 19:00-22:00
Salón: 28106
DATOS DEL DOCENTE
Nombre: Oscar Alonso Rosete Beas
E-mail: oscar.rosete@cetys.mx
oscarrosete.com

oscarrosete.com
25/01
PROPÓSITO DEL CURSO
Esta asignatura tiene como propósito introducir al estudiante en los conceptos fundamentales relacionados al diseño y síntesis de mecanismos.
Durante el curso se estudiará:
-
El estudio cinemático y diseño de levas y engranajes
-
La síntesis/diseño y análisis de mecanismos.
-
Análisis de movilidad de Gruebler
-
Criterio de discernimiento de Grashoff
-
Estudio de vibraciones y balanceo estático y dinámico de maquinaria
oscarrosete.com

25/01
Introducción a la materia
Las actividades que se realicen dentro del aula serán dirigidas por el profesor y otras serán de carácter independiente para ser realizadas por los alumnos fuera del aula.
Las formas genéricas de actividades de aprendizaje que serán realizadas por los alumnos son:
- Trabajo colaborativo dentro del aula para analizar y debatir sobre los contenidos y bajo la dirección del profesor.
- Exposición de contenidos por parte del profesor y alumnos
- Aprendizaje basado en proyectos de aplicación por equipos o individuales.
oscarrosete.com
oscarrosete.com

oscarrosete.com
25/01
EVIDENCIAS DE DESEMPEÑO
- Reportes de análisis y resolución de casos de estudio y ejercicios de aplicación.
-
Reportes de lectura y reportes de investigación.
-
Prácticas de Laboratorio(*)
-
Presentaciones en clase.
-
Elaboración de prototipos.
-
Exámenes escritos a lo largo del curso y examen final.
-
Proyecto final integrador en donde se apliquen las herramientas vistas durante el curso.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Durante el curso el alumno tendrá la oportunidad de aplicar sus conocimientos en el área de diseño mecánico, utilizar paquetes computacionales para la modelación de elementos, manipular y realizar un proyecto de Mecanismos integrado.


Agenda
oscarrosete.com

oscarrosete.com
25/01
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
- Levas, con diferentes tipos de seguidores.
- Bases del diseño de levas
- Engranajes cilíndricos de dientes rectos, Involumetría y Nomenclatura.
- Engranajes Cónicos.
- Análisis de transmisión de velocidad en engranajes
Unidad 2: Análisis cinemático de Levas y Engranajes
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
- Espaciado de puntos de precisión.
- Síntesis de un 4 barras generación de función.
- Síntesis de un 4 barras para valores instantáneos de la velocidad y aceleración angulares.
- Síntesis de un 4 barras para 3 posiciones del acoplados
Unidad 3: Introducción a la síntesis de mecanismos.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
- Movimientos de una partícula
- Lineal.
- Angular.
- Relativo.
- Métodos de análisis de velocidad y aceleración.
- Análisis de velocidad y aceleración mediante matemáticas vectoriales.
- Análisis de velocidad por
- Centros instantáneos.
- Teorema de Kennedy.
- Componente de Coriólisis de aceleración.
Unidad 4: Cinemática de maquinas
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
- Vibración natural.
- Vibración forzada.
- Amortiguación.
- Rotación excéntrica de flechas.
- Frecuencia natural y velocidad crítica.
Unidad 5: Vibración de Maquinas.
oscarrosete.com

oscarrosete.com
POLÍTICAS ENTREGAS
- Existe tolerancia de 5 minutos de llegada tardía, a partir de los cuales se tomará asistencia.
- Las fechas de entrega y presentación para exámenes parciales, tareas, exposiciones, prácticas y trabajo final son Inamovibles.
- No se aceptarán entregas de exámenes fuera de la fecha y hora establecida y la calificación de una falta de entrega o entrega extemporánea es cero.
oscarrosete.com

oscarrosete.com
- Se aceptarán entregas de tareas/prácticas fuera de las fechas y horas establecidas (calificación de falta de entrega es cero).
- Penalización 10%/ día en tareas
- Penalización 10%/ semana en práctica.
- Todas las entregas deberán realizarse por medio definido en clase, de acuerdo a las indicaciones dadas (blackboard y pdf generalmente).
POLÍTICAS ENTREGAS
oscarrosete.com

oscarrosete.com
POLÍTICAS MATERIAL
- El material para trabajar en clase, descripción de tareas y temas para exposición, así como cualquier material de apoyo estará disponible a través del Blackboard o el sitio web y este será actualizado periódicamente.
- Es responsabilidad de cada estudiante traer a la sesión de clase el material que indique el maestro, incluyendo exposiciones y tareas.
oscarrosete.com

oscarrosete.com
POLÍTICAS PRESENTACIONES
- Preparar una presentación formal e interactiva que presente al grupo el tema correspondiente (Prezi, PowerPoint, Google Slides, otro).
- Preparar un reporte escrito de los puntos más relevantes de la presentación, así como las referencias consultadas.
- Subir en la actividad correspondiente en Blackboard la presentación y el reporte escrito.
- Es necesario estar presente en las actividades de exposición, de lo contrario la calificación para la exposición es cero.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Bibliografía
Robert L. Norton. Diseño de Maquinaria Síntesis y Análisis de maquinas y Mecanismos. McGraw Hill
Mabie y Ockvirk. (Texto) Mechanisms and Dynamics of Machinery.Limusa Wiley
Shigley J. E., Uicker. Theory of Machines and Mechanisms. McGraw Hill
Hartenberg and Denavit. Kinematic Synthesis of Linkages. McGraw Hill



oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Software:
Working Model, Solidworks Motion
Herramientas digitales:
Blackboard, Google suite, recursos microsoft, portafolio electronico, bases de datos.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
| Concepto | Descripción | Ponderación |
|---|---|---|
| Examenes | Pruebas objetivas en forma de exámenes parciales y/o finales que se pueden realizar de manera individual o por equipos. |
30% |
| Tareas | Resolución de ejemplos típicos, solución de problemas en Tareas individuales y en equipo. | 15% |
| Prácticas (Ejercicios apoyados con software) | Diseño de elementos mecánicos por computadora. Usando un software especializado. |
10% |
| Desarrollo y Exposición de prototipos de mecanismos | Elaboración de prototipos físicos de acuerdo al contenido visto en clase. | 15 % |
| Proyectos. | Desarrollo y presentaciones profesionales de los proyectos | 30% |
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Profesor:
Ing. Oscar Alonso Rosete Beas
E-Mail:
oscar.rosete@cetys.mx
Pagina de facebook:
https://www.facebook.com/oscararosete
Sitio web:
https://oscarrosete.com/
oscarrosete.com

oscarrosete.com
25/01
Contacto preferente para dudas

Asesorías: WhatsApp 686 264 5073
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Enlaces relevantes:
http://bibliotecadigital.cetys.mx/
http://courses.csail.mit.edu/6.S080/lectures/02_all.pdf
http://www.mekanizmalar.com/index.html
http://www.technologystudent.com/cams/camdex.htm
http://www.softintegration.com/chhtml/toolkit/mechanism/fourbar/



oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia



oscarrosete.com
oscarrosete.com
25/01
Introducción a la materia
Formación de equipos para presentaciones y proyecto final.



oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Tarea 1. Investigue el significado de los siguientes términos:
- Dinámica de maquinaria
- Mecanismo, y que acepciones tiene en el idioma ingles.
- ¿Cual es la diferencia entre maquina y mecanismo?
- ¿Cual Mecanismo se considera es el mas importante y porque?

oscarrosete.com
oscarrosete.com
25/01
Introducción a la materia
Tarea 1. Investigue el significado de los siguientes términos:
- ¿Cual es la diferencia entre Análisis y Síntesis?
- ¿Por qué se deben balancear los rotores?
Nota: Toda tarea debe subirse a blackboard en un solo archivo cuyo nombre sea:
No de matricula – Tarea No
Ejemplo: 13256 Tarea 1

Agenda
oscarrosete.com

oscarrosete.com
25/01
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Se explora la cinemática y la dinámica de maquinaria con respecto a la síntesis de mecanismos para lograr los movimientos o tareas requeridas, así como el análisis de mecanismos para determinar su comportamiento dinámico de cuerpo rígido.
Estos temas son fundamentales en el tema más amplio de diseño de máquinas. Sobre la premisa de que no se puede analizar algo hasta que sea sintetizado dentro de su existencia, primero se explorará el tema de síntesis de mecanismos.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Se explora la cinemática y la dinámica de maquinaria con respecto a la síntesis de mecanismos para lograr los movimientos o tareas requeridas, así como el análisis de mecanismos para determinar su comportamiento dinámico de cuerpo rígido.
Estos temas son fundamentales en el tema más amplio de diseño de máquinas.

oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Un mecanismo es un sistema de elementos acomodados para transmitir movimiento de una forma predeterminada.
Por lo general desarrolla fuerzas muy bajas y transmite poca potencia.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Una máquina, en general, contiene mecanismos que están diseñados para producir y transmitir fuerzas significativas.
Transmite movimiento y energia de forma determinada.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
No existe una clara línea divisoria entre mecanismos y máquinas. Difieren en su grado y no en su clase.
Si las fuerzas o niveles de energía en el dispositivo son significativos, se considerará como una máquina; si no es así, será considerado como un mecanismo.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Ejemplos de mecanismos pueden ser un sacapuntas, un obturador de cámara fotográfica, un reloj análogo, una silla plegable, una lámpara de escritorio ajustable y un paraguas.



oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Ejemplos de máquinas un procesador de alimentos, la puerta de la bóveda de un banco, la transmisión de un automóvil, una niveladora, un robot y un juego mecánico de un parque de diversiones.


oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Cuerpo rígido
Un cuerpo rígido es teóricamente un cuerpo sólido de tamaño finito, en el que las deformaciones originadas por cualquier carga, son despreciables, de manera que la distancia entre dos puntos cualquiera en el mismo, es siempre una constante.

oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
TIPOS DE MOVIMIENTO
Un cuerpo rígido libre de moverse dentro de un marco de referencia, en el caso general, tendrá movimiento complejo, el cual es una combinación simultánea de rotación y traslación.
La traslación y rotación representan movimientos independientes del cuerpo. Cada uno puede presentarse sin el otro.

oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Para simplificar, se limitará este análisis al caso de sistemas cinemáticos planos (2-D). Para este propósito, se definirán estos términos en movimiento plano como sigue:
- Rotación pura
El cuerpo posee un punto (centro de rotación) que no tiene movimiento con respecto al marco de referencia “estacionario”. Todos los demás puntos del cuerpo describen arcos alrededor del centro. Una línea de referencia trazada en el cuerpo a través del centro cambia sólo su orientación angular.
oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Traslación pura
Todos los puntos del cuerpo describen trayectorias paralelas (curvilíneas o rectilíneas). Una línea de referencia trazada en el cuerpo cambia su posición lineal pero no su orientación angular.

oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Movimiento complejo
Una combinación simultánea de rotación y traslación. Cualquier línea de referencia trazada en el cuerpo cambiará tanto su posición lineal como su orientación angular. Los puntos en el cuerpo recorrerán trayectorias no paralelas, y habrá, en todo instante, un centro de rotación, el cual cambiará continuamente de ubicación.

oscarrosete.com

oscarrosete.com
25/01
Introducción a la materia
Movimiento complejo
Una combinación simultánea de rotación y traslación. Cualquier línea de referencia trazada en el cuerpo cambiará tanto su posición lineal como su orientación angular. Los puntos en el cuerpo recorrerán trayectorias no paralelas, y habrá, en todo instante, un centro de rotación, el cual cambiará continuamente de ubicación.

oscarrosete.com

oscarrosete.com
25/01
Eslabones, juntas y cadenas cinemáticas
Los eslabonamientos son los bloques de construcción básicos de todos los mecanismos.
Los eslabonamientos se componen de eslabones y juntas.
Un eslabón, es un cuerpo rígido (supuesto) que posee por lo menos dos nodos que son puntos de unión con otros eslabones.
oscarrosete.com

oscarrosete.com
25/01
Eslabones
Un eslabón es un cuerpo rígido (supuesto) que posee por lo menos dos nodos que son puntos de unión con otros eslabones.
Eslabón binario el que tiene dos nodos.
Eslabón ternario el que tiene tres nodos.
Eslabón cuaternario el que tiene cuatro nodos.


oscarrosete.com

oscarrosete.com
25/01
Eslabones
Otra clasificación de los mecanismos tiene que ver con el tipo de movimiento que representan. Independientemente de la forma del eslabón y(o) la función que desempeñan, estos pueden clasificarse en función del movimiento como:
1. Manivela.
2. Biela.
3. Corredera.
oscarrosete.com

oscarrosete.com
25/01
Eslabones
La manivela es el eslabón que representa el movimiento de rotación alrededor de un nodo fijo; cuando las revoluciones no son completas, entonces específicamente se le conoce como oscilador.
Una corredera es el eslabón que representa el movimiento de translación rectilínea sobre una referencia o guía fija.
La biela representa el movimiento donde todos los nodos se encuentran en movimiento.
oscarrosete.com

oscarrosete.com
25/01
Eslabones
Considérense los componentes del motor de combustión interna. Este mecanismo convierte el movimiento reci- procante (rectilíneo) del pistón en un movimiento circular del cigüeñal. En términos cinemáticos, los eslabones son la corredera, que representa al pistón, la manivela, que representa al cigüeñal, y la biela.

oscarrosete.com

oscarrosete.com
25/01
Eslabones
Considérese el mecanismo utilizado en máquinas de costura.
En este caso, el mecanismo convierte el tipo de movimiento circular de la manivela en uno lineal, correspondiente a la base de la aguja, mediante un elemento intermedio llamado biela.

oscarrosete.com

oscarrosete.com
25/01
Eslabones
Máquinas de costura antiguas para impulsar el disco excéntrico. En este mecanismo, la palanca utilizada como elemento impulsor es una manivela, específicamente un oscilador, el disco excéntrico es una manivela, mientras que el elemento que une estos dos eslabones es una biela.

oscarrosete.com

oscarrosete.com
25/01
Junta/ Joint
Una junta es una conexión entre dos o más eslabones (en sus nodos), la cual permite algún movimiento, o movimiento potencial, entre los eslabones conectados.


oscarrosete.com

oscarrosete.com
25/01
Junta/ Joint
Las juntas (también llamadas pares cinemáticos) se pueden clasificar de varias maneras:
1 Por el tipo de contacto entre los elementos, de línea, de punto o de superficie.
2 Por el número de grados de libertad permitidos en la junta.
3 Por el tipo de cierre físico de la junta: cerrada por fuerza o por forma.
4 Por el número de eslabones unidos (orden de la junta).

oscarrosete.com

oscarrosete.com
25/01
Tipos de juntas
Clasificación de acuerdo al tipo de contacto:

Pares inferiores
Aquellos en los que el contacto de unión entre los dos cuerpos ocurre a través de una superficie.
Pares superiores
Aquellos en los que el contacto se realiza a través de un punto o una línea.

oscarrosete.com

oscarrosete.com
25/01
Tipo de contacto
Los seis pares cinemáticos inferiores

oscarrosete.com

oscarrosete.com
25/01
Ejemplos de pares superiores
Tienen contacto a través de un punto o una línea.



Tipo de contacto
oscarrosete.com

oscarrosete.com
25/01

Tipo de contacto
Ejemplos de pares superiores
Tienen contacto a través de un punto o una línea.
oscarrosete.com

oscarrosete.com
25/01
Tipos de juntas
Tipos de juntas por grados de libertad

oscarrosete.com

oscarrosete.com
25/01
Tipos de juntas (GDL)
Junta Revoluta (R)
1 GDL, solo movimiento de rotacion






oscarrosete.com

oscarrosete.com
25/01
Junta prismática (P)
1 GDL solo movimiento traslación o deslizamiento entre los eslabones.




Tipos de juntas (GDL)
oscarrosete.com

oscarrosete.com
25/01
Junta prismática (P)
1 GDL solo movimiento traslación o deslizamiento entre los eslabones.


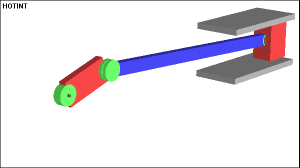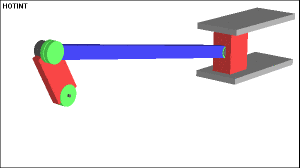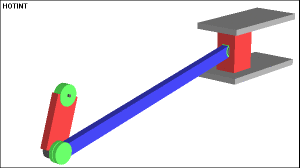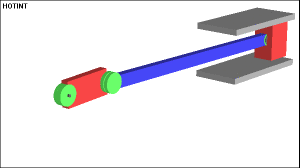
Tipos de juntas (GDL)
oscarrosete.com

oscarrosete.com
25/01
Junta helicoidal/helical (H)
1 GDL, solo movimiento rotación

Tipos de juntas (GDL)
oscarrosete.com

oscarrosete.com
25/01
Junta cilíndrica (C)
2 GDL, traslación y rotación


Tipos de juntas (GDL)
oscarrosete.com

oscarrosete.com
25/01
Junta esférica (S)
3 GDL, solo rotación



Tipos de juntas (GDL)
oscarrosete.com

oscarrosete.com
25/01
Junta plana (p)
3 GDL, 2 movimientos traslación y 1 de rotación

Tipos de juntas (GDL)
oscarrosete.com
Actividad en equipo
En equipos, seleccionen un producto o sistema mecánico que de acuerdo a los conceptos vistos en el curso pueda ser considerado mecanismo y uno que pueda ser considerado una máquina.
- Identificar y clasificar las juntas que lo componen.
- Identificar y clasificar los eslabones que lo componen.
Deberá generarse una presentación y subirse a actividad correspondiente de blackboard.
oscarrosete.com

Agenda
oscarrosete.com

oscarrosete.com
02/02
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com
Actividad en equipo
En equipos, seleccionen un producto o sistema mecánico que de acuerdo a los conceptos vistos en el curso pueda ser considerado mecanismo y uno que pueda ser considerado una máquina.
- Identificar y clasificar las juntas que lo componen.
- Identificar y clasificar los eslabones que lo componen.
Deberá generarse una presentación y subirse a actividad correspondiente de blackboard.
oscarrosete.com


02/02
oscarrosete.com
Mecanismos
oscarrosete.com

02/02

oscarrosete.com

oscarrosete.com
Junta/ Joint
Las juntas (también llamadas pares cinemáticos) se pueden clasificar de varias maneras:
1. Por el tipo de contacto entre los elementos, de línea, de punto o de superficie.
2. Por el número de grados de libertad permitidos en la junta.
3. Por el tipo de cierre físico de la junta: cerrada por fuerza o por forma.
4. Por el número de eslabones unidos (orden de la junta).

02/02
oscarrosete.com

oscarrosete.com
Tipos de juntas
Clasificación de acuerdo al tipo de contacto:

Pares inferiores
Aquellos en los que el contacto de unión entre los dos cuerpos ocurre a través de una superficie.
Pares superiores
Aquellos en los que el contacto se realiza a través de un punto o una línea.

02/02
oscarrosete.com

oscarrosete.com
Tipos de juntas
Tipos de juntas por grados de libertad

02/02
oscarrosete.com

oscarrosete.com
Tipos de juntas
Una junta con cierre de fuerza, un pasador en un semicojinete o una corredera sobre una superficie, requieren alguna fuerza externa para mantenerlas en contacto o cerradas.
Esta fuerza podría ser suministrada por la gravedad, un resorte o cualquier medio externo

02/02
oscarrosete.com

oscarrosete.com
25/01
Tipos de juntas
Una junta con cierre de forma se mantiene unida o cerrada por su geometría. Un pasador en un orificio o una corredera en una ranura de dos caras son juntas con cierre de forma.


oscarrosete.com

oscarrosete.com
Tipos de juntas
El orden de una junta es menor en uno que el número de eslabones unidos.

02/02
oscarrosete.com

oscarrosete.com
Cadena cinemática
Cadena cinemática:
Un ensamble de eslabones y juntas interconectados de modo que produzcan un movimiento controlado en respuesta a un movimiento suministrado.

02/02
oscarrosete.com

oscarrosete.com
Cadena cinemática
Las cadenas cinemáticas, pueden ser abiertas o cerradas.
Un cadena cerrada no tendrá pares o nodos abiertos y puede no tener grados de libertad.
Una cadena abierta siempre tendrá mas de un grado de libertad, por lo que requerirá de tantos motores o servos como grados de libertad tenga.
A una cadena cinemática abierta de dos eslabones binarios y un par se le llama díada.
02/02
oscarrosete.com

oscarrosete.com
Mecanismos
Mecanismo:
Una cadena cinemática en la cual por lo menos un eslabón se ha “fijado” o sujetado al marco de referencia (el cual por sí mismo puede estar en movimiento).
Mediante los mecanismos se pretende obtener y controlar movimientos específicos.
02/02
oscarrosete.com

oscarrosete.com
Mecanismos
Una cadena cinemática no dispone de un eslabón fijo, pero cuando se selecciona uno de sus elementos como eslabón fijo, entonces forma un mecanismo.

02/02
oscarrosete.com

oscarrosete.com
Mecanismos
Mecanismo cerrado: Un mecanismo cerrado no tendrá puntos de fijación abiertos o nodos, y puede tener uno o más grados de libertad. Se forma a partir de una cadena cerrada.
Mecanismo abierto: siempre tendrá más de un grado de libertad, por lo que requiere tantos actuadores (motores) como grados de libertad tenga.

02/02
oscarrosete.com

oscarrosete.com
Mecanismos
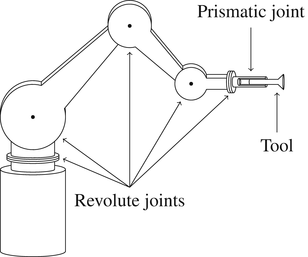
Ejemplo común de un mecanismo abierto es un robot industrial.

02/02
oscarrosete.com

Tipos de mecanismos
En general se pueden obtener mecanismos planares y espaciales.
Mecanismo planar es aquel en el que el movimiento de los eslabones es paralelo a un plano de referencia.
En general los únicos pares que pueden utilizarse para construir mecanismos planos son el de revoluta y el prismático.
oscarrosete.com

02/02
oscarrosete.com

Tipos de mecanismos
Mecanismo espacial es aquel cuyos elementos pueden moverse en las tres dimensiones.
Los otros cuatro pares inferiores conocidos, se utilizan para construir mecanismos espaciales o tridimensionales.
oscarrosete.com
02/02
oscarrosete.com

oscarrosete.com
Máquina
Una maquina es un mecanismo o conjunto de mecanismos, cuyo propósito es el de transmitir una fuerza desde una fuente, vencer las resistencias que se presenten y realizar un trabajo.
Una maquina es un mecanismo pero un mecanismo puede no ser una maquina.

02/02
oscarrosete.com
Actividad individual
- Instalar Working Model
- Seguir tutorial de manejo del software
- Investigar mecanismo biela–manivela–corredera y simular
- Subir a blackboard el resultado
oscarrosete.com
02/02


Agenda
oscarrosete.com

oscarrosete.com
04/02
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
El análisis de mecanismos requiere que se dibujen diagramas cinemáticos claros, simples y esquemáticos de los eslabones y juntas con los que están formados dichos mecanismos.
Un diagrama cinemático es la representación gráfica de un mecanismo mediante elementos simples, como líneas, rectángulos, etcétera, y solo denota la cinemática del mismo.
04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Los eslabones reales pueden tener cualquier forma, pero un eslabón “cinemático”, o borde de eslabón, se define como una línea entre juntas que permite el movimiento relativo entre eslabones adyacentes.
Las juntas pueden permitir rotación, traslación o ambos movimientos entre los eslabones unidos. Los movimientos posibles de la junta deben ser claros y obvios en el diagrama cinemático.
04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos






04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos








04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Para elaborar un diagrama cinemático se dispone de los siguientes componentes:
Manivela
Biela
Corredera
Rueda
04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Una manivela está representada por una línea dirigida desde la articulación fija hacia el nodo de interés. Como se puede ver, en la figura se representa una manivela de dos y tres nodos.
Una biela tiene una representación similar a una manivela, con la única diferencia de que no tiene articulación fija.


04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Una corredera se representa como un elemento rectangular que se desliza sobre una superficie fija.
Una rueda, aunque es un elemento con movimiento circular alrededor de un nodo fijo, no se considera como manivela, ya que la transmisión del movimiento no es por revoluta sino por contacto directo.


04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Ejemplos de diagramas cinemáticos


04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Ejemplos de diagramas cinemáticos


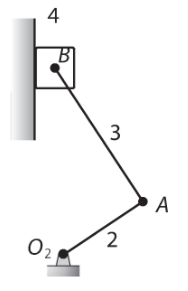

04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos

04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Ejemplos de diagramas cinemáticos
La figura es de una máquina que se usa para cortar y ajustar tableros de circuitos electrónicos impresos. Elabore un diagrama cinemático



04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Ejemplos de diagramas cinemáticos
1. Identifique la bancada.
El primer paso en la elaboración de un diagrama cinemático es decidir la parte que se diseñará como la bancada. El movimiento de todos los demás eslabones se determinará en relación con la bancada.
En algunos casos, la selección es evidente porque la bancada está firmemente sujeta en el suelo.
La base grande atornillada a la mesa se designa como la bancada.
04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
2. Identifique todos los demás eslabones
Una observación cuidadosa revela otras tres partes que se mueven:
Eslabón 2: Mango
Eslabón 3: Cuchilla cortante
Eslabón 4: Barra que conecta la cuchilla con el mango.

04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
3. Identifique las uniones
Se utilizan pernos para unir el eslabón 1 al 2, el eslabón 2 al 3 y el eslabón 3 al 4. Tales uniones se identifican con las letras A a C.
Además, el cortador se desliza hacia arriba y hacia abajo, a lo largo de la base. Esta unión de corredera conecta el eslabón 4 con el 1 y se identifica con la letra D.

04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Ejemplos de diagramas cinemáticos
4. Identifique los puntos de interés.
Por último, se desea conocer el movimiento en el extremo del mango, que se identifica como el punto de interés X.
5. Elabore el digrama cinemático

04/02
oscarrosete.com

oscarrosete.com
Diagramas cinemáticos
Diagrama cinemático

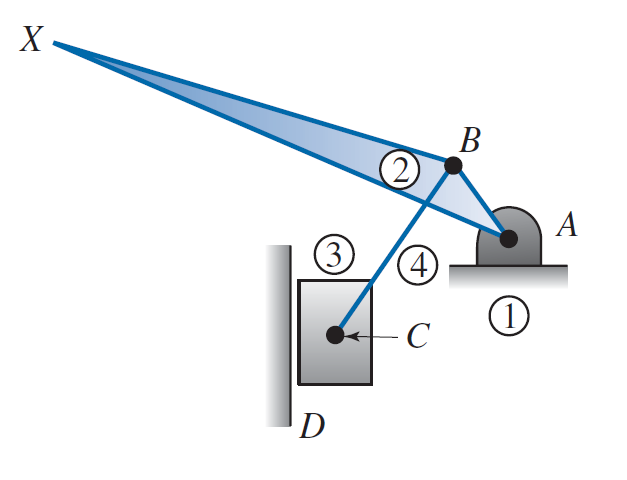
04/02
oscarrosete.com

oscarrosete.com
04/02
oscarrosete.com
Actividad en equipo
En equipos, seleccionen un producto o sistema mecánico que de acuerdo a los conceptos vistos en el curso pueda ser considerado mecanismo y uno que pueda ser considerado una máquina.
- Identificar y clasificar las juntas que lo componen.
- Identificar y clasificar los eslabones que lo componen.
- Elaborar su diagrama cinemático
Deberá generarse una presentación y subirse a actividad correspondiente de blackboard.
oscarrosete.com

oscarrosete.com

oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos

Considérese los siguientes mecanismos y elabore su diagrama cinemático:

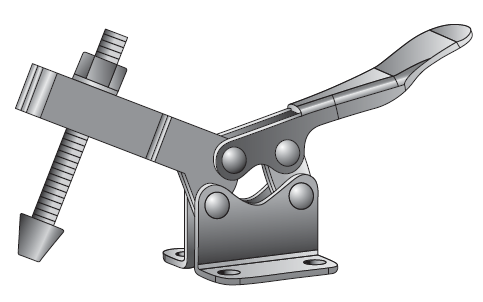


04/02

oscarrosete.com

oscarrosete.com
Clasificación de mecanismos
Ante el hecho de que las representaciones cinemáticas permiten representar cualquier mecanismo de n barras en una forma simple, los mecanismos se pueden clasificar en familias que representan los componentes principales de su movilidad.
1. Mecanismos de barras articuladas
- Mecanismos de manivela-biela-corredera, o RRRP.
- Mecanismos de cuatro barras, o RRRR.
- Diadas.
2. Mecanismos de contacto directo
- Por deslizamiento.
- Por rodamiento
- Ruedas.
04/02
oscarrosete.com

oscarrosete.com
Mecanismos manivela-biela-corredera
Aun cuando los mecanismos de combustión interna y la máquina de costura de la parecen no tener nada en común, en términos cinemáticos son lo mismo, ya que ambos están formados por los eslabones de manivela- biela-corredera; por tanto, una representación única de ambos mecanismos y otros similares se puede observar en la figura
04/02

oscarrosete.com

oscarrosete.com
Mecanismos manivela-biela-corredera
En la figura se puede ver el conocido mecanismo manivela-corredera, o bien como RRRP, ya que las articulaciones O2, A y B y el contacto deslizante de la corredera 4 son Revoluta, Revoluta, Revoluta y Prisma, respectivamente.
04/02

oscarrosete.com

oscarrosete.com
Mecanismos manivela-biela-corredera
Los nodos móviles son asignados mediante una letra y los nodos fijos por la letra O (de origen) y un número (el correspondiente al número del eslabón que articula). Los eslabones se enumeran a partir del 2, ya que el número 1 se reserva al elemento fijo.
04/02

oscarrosete.com
oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos
- Identificar una aplicación del mecanismo biela-manivela-corredera, también llamado slider-crank mechanism y documentarla en una presentación.
- Realizar su propio mecanismo planar, biela-manivela-corredera a mostrar en clase
04/02


Mecanismo que impulsa una bomba de agua manual
Slider-crank kinematic diagram
oscarrosete.com
oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos
- Identificar una aplicación del mecanismo biela-manivela-corredera, también llamado slider-crank mechanism y documentarla en una presentación.
- Realizar su propio mecanismo planar, biela-manivela-corredera a mostrar en clase
04/02
oscarrosete.com
oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos
- Identificar una aplicación del mecanismo biela-manivela-corredera, también llamado slider-crank mechanism y documentarla en una presentación.
- Realizar su propio mecanismo planar, biela-manivela-corredera a mostrar en clase
04/02
Tutorial

Agenda
oscarrosete.com

oscarrosete.com
11/02
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com
oscarrosete.com
Actividad Individual
Inversión cinemática
El movimiento absoluto se mide con respecto a una bancada estacionaria.
El movimiento relativo de un punto o un eslabón se mide con respecto a otro eslabón.
11/02

oscarrosete.com
oscarrosete.com
Actividad Individual
Inversión cinemática
Cuando se seleccionan diferentes eslabones como bancada, no se altera el movimiento relativo de los eslabones sin embargo, el movimiento absoluto puede ser significativamente diferente.
El uso de eslabones alternos como eslabones fijos se conoce como inversión cinemática.
11/02

oscarrosete.com
oscarrosete.com
Actividad Individual
Inversión cinemática
11/02

oscarrosete.com
oscarrosete.com
Actividad Individual
Grado de libertad o movilidad
El concepto de grado de libertad (GDL) es fundamental tanto para la síntesis como para el análisis de mecanismos. Es necesario ser capaz de determinar rápidamente el GDL de cualquier conjunto de eslabones o juntas que pueda ser sugerido como solución a un problema.
El grado de libertad (también llamado movilidad M) de un sistema se define como
11/02

oscarrosete.com
oscarrosete.com
Actividad Individual
El número de entradas que se necesita proporcionar para crear una salida predecible.
El número de coordenadas independientes requerido para definir su posición.
11/02

Grado de libertad
oscarrosete.com
oscarrosete.com
Actividad Individual
Para determinar el GDL global de cualquier mecanismo, se debe considerar el número de eslabones, así como las juntas y las interacciones entre ellos.
El GDL de cualquier ensamble de eslabones se puede pronosticar con una investigación de la condición de Gruebler
11/02

Grado de libertad
oscarrosete.com
oscarrosete.com
Actividad Individual
- Cualquier eslabón en un plano tiene tres GDL
- Cuando estos eslabones están conectados por una junta completa elimina dos GDL
- Cualquier eslabón está conectado a tierra o unido al marco de referencia, se eliminarán sus tres GDL.
Este razonamiento lleva a la ecuación de Gruebler
11/02

Grado de libertad
oscarrosete.com
oscarrosete.com
Actividad Individual
11/02



Grado de libertad

oscarrosete.com
oscarrosete.com
Actividad Individual
11/02


Ecuación de Gruebler
Hay que observar que en cualquier mecanismo real, aun cuando mas de un eslabon de la cadena cinematica este conectado a tierra, el efecto neto sera crear un eslabon conectado a tierra de mayor orden y mas grande, ya que solo puede haber un plano de tierra. Por lo tanto, G siempre es uno y la ecuacion de Gruebler se convierte en :


oscarrosete.com
oscarrosete.com
Actividad Individual
11/02


Ecuación de Gruebler
El valor de J en las ecuaciones debe reflejar el valor de todas las juntas en el mecanismo. Esto es, las semijuntas cuentan como 1/2 porque solo eliminan un GDL. Esto es menos confuso si se utiliza la modificacion de Kutzbachh de la ecuacion de Gruebler en esta foroma:
J1 (pernos o correderas) J2 (levas o engranes)

oscarrosete.com
oscarrosete.com
Actividad Individual
11/02

Ecuación de Gruebler
El numero de grados de libertad del eslabonamiento o movilidad(M)
Se puede definir como el numero de actuadores necesarios para operar el mecanismo.
Un mecanismo actuador podría ser el movimiento manual de un eslabón hacia otra posición, la conexión de un motor al eje de un eslabón o el empuje del pistón de un cilindro hidráulico.
oscarrosete.com
oscarrosete.com
Actividad Individual
11/02

Ecuación de Gruebler

Un grado de libertad
M=1
Mecanismo bloqueado M=1
Múltiples grados de libertad
M=2
oscarrosete.com

oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos

Considérese los siguientes mecanismos y elabore su diagrama cinemático:
Determinar su movilidad





11/02
oscarrosete.com

oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos
11/02


oscarrosete.com

oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos

Considérese los siguientes mecanismos y elabore su diagrama cinemático:
Determinar su movilidad





16/02
oscarrosete.com

oscarrosete.com
SÍNTESIS DE NÚMERO
16/02
Síntesis el proceso de desarrollar un mecanismo a partir de un conjunto de requerimientos de desempeño
- Síntesis dimensional
- Síntesis de tipo
- Síntesis de numero
El análisis asegura que el mecanismo exhibirá movimiento que lograra el conjunto de requerimientos.

oscarrosete.com

oscarrosete.com
SÍNTESIS DE NÚMERO
16/02
El término síntesis de número significa la determinación del número y orden de eslabones y juntas necesarios para producir movimiento de un GDL en particular.
En este contexto orden de eslabón se refiere al número de nodos por eslabón, es decir, binario, ternario, cuaternario, etc.

oscarrosete.com

oscarrosete.com
SÍNTESIS DE NÚMERO
16/02
El valor de síntesis de número permite la exhaustiva determinación de todas las posibles combinaciones de
eslabones que producirán cualquier GDL elegido.
Esto equipa entonces al diseñador con un catálogo
definitivo de eslabonamientos potenciales para resolver una variedad de problemas de control de movimiento.

oscarrosete.com

oscarrosete.com
Mecanismos
Mecanismo cerrado: Un mecanismo cerrado no tendrá puntos de fijación abiertos o nodos, y puede tener uno o más grados de libertad. Se forma a partir de una cadena cerrada.
Mecanismo abierto: siempre tendrá más de un grado de libertad, por lo que requiere tantos actuadores (motores) como grados de libertad tenga.

16/02
oscarrosete.com

oscarrosete.com
Eslabones
Un eslabón es un cuerpo rígido (supuesto) que posee por lo menos dos nodos que son puntos de unión con otros eslabones.
Eslabón binario el que tiene dos nodos.
Eslabón ternario el que tiene tres nodos.
Eslabón cuaternario el que tiene cuatro nodos.
No aplicable a bancada de mecanismos abiertos

16/02

oscarrosete.com

oscarrosete.com
Eslabones (Final)
Un eslabón es un cuerpo rígido (supuesto) que posee movimiento relativo respecto a otro cuerpo rígido.
Eslabón unitario el que tiene un nodo.
Eslabón binario el que tiene dos nodos.
Eslabón ternario el que tiene tres nodos.
Eslabón cuaternario el que tiene cuatro nodos.
16/02

oscarrosete.com

oscarrosete.com
Junta/ Joint
Una junta es una conexión entre dos o más eslabones (en sus nodos), la cual permite algún movimiento relativo, o movimiento potencial, entre los eslabones conectados.


16/02
oscarrosete.com

oscarrosete.com
Tipos de juntas (GDL)
Junta Revoluta (R)
1 GDL, solo movimiento de rotacion






16/02
oscarrosete.com

oscarrosete.com
Junta prismática (P)
1 GDL solo movimiento traslación o deslizamiento entre los eslabones.




Tipos de juntas (GDL)
16/02
oscarrosete.com
oscarrosete.com
Actividad Individual


Ecuación de Gruebler
El valor de J en las ecuaciones debe reflejar el valor de todas las juntas en el mecanismo. Esto es, las semijuntas cuentan como 1/2 porque solo eliminan un GDL. Esto es menos confuso si se utiliza la modificacion de Kutzbachh de la ecuacion de Gruebler en esta foroma:
J1 (pernos o correderas) J2 (levas o engranes)

16/02
oscarrosete.com

oscarrosete.com
Casos especiales
16/02
La movilidad es una propiedad extremadamente importante de un mecanismo ya que brinda información acerca del número de actuadores requeridos para operar un mecanismo.
Uniones coincidentes
Físicamente utilizamos un perno, por definición, una unión de perno conecta dos eslabones, se modela como dos uniones separadas.

oscarrosete.com

oscarrosete.com
Casos especiales
16/02
Uniones coincidentes
Físicamente utilizamos un perno, por definición, una unión de perno conecta dos eslabones, se modela como dos uniones separadas.
Una unión juntaría el primer y segundo, la segunda unión juntaría el segundo y tercer eslabón



oscarrosete.com

oscarrosete.com
Casos especiales
16/02
Uniones coincidentes
Físicamente utilizamos un perno, por definición, una unión de perno conecta dos eslabones, se modela como dos uniones separadas.

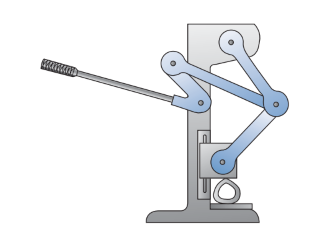
oscarrosete.com

oscarrosete.com
Casos Gruebler
16/02
Mecanismo
Existen solo tres posibilidades. Si el GDL es positivo, será un mecanismo, y los eslabones tendrán movimiento relativo.

oscarrosete.com

oscarrosete.com
16/02
Estructura
Si el GDL es exactamente cero, entonces se tendrá una estructura, lo que significa que ningún movimiento es posible.

Casos Gruebler
Casos Gruebler
oscarrosete.com

oscarrosete.com
16/02
Estructura precargada
Si el GDL es negativo, entonces se tendrá una estructura precargada, lo que significa que no será posible ningún movimiento y que algunos esfuerzos también pueden estar presentes en el momento del ensamble.


Casos Gruebler
oscarrosete.com

oscarrosete.com
Paradojas de Gruebler
16/02
La ecuacion de Gruebler no toma en cuenta la geometria de los eslabones, en raras ocasiones esto causa resultados erroneos.


Excepciones geométricas
oscarrosete.com

oscarrosete.com
Paradojas de Gruebler
16/02
Excepciones geométricas
El eslabonamiento de la izquierda tiene cinco eslabones y seis uniones de perno, lo que nos diría cero grados de libertad. Sin embargo seria capaz de moverse con un grado de libertad. El eslabón central es redundante.
Hay varios ejemplos de mecanismos que transgreden la ecuación debido a su geometría única.



oscarrosete.com

oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos

Considérese los siguientes mecanismos y elabore su diagrama cinemático:
Determinar su movilidad





16/02
oscarrosete.com
oscarrosete.com
oscarrosete.com
Actividad en equipo
En equipos, seleccionen un producto o sistema mecánico que de acuerdo a los conceptos vistos en el curso pueda ser considerado mecanismo y uno que pueda ser considerado una máquina.
- Identificar y clasificar las juntas que lo componen.
- Identificar y clasificar los eslabones que lo componen.
- Elaborar su diagrama cinemático
- Determinar su movilidad
Deberá generarse una presentación y subirse a actividad correspondiente de blackboard.
oscarrosete.com
16/02

oscarrosete.com

oscarrosete.com

El eslabonamiento más simple y más comun es el de cuatro barras. Una combinación de cuatro eslabones, uno designado como la bancada y conectado por cuatro uniones de perno.
Se muestra como referencia el mecanismo de un limpiador para el cristal.
Mecanismos de 4 barras
Introducción
16/02

oscarrosete.com

oscarrosete.com

Al considerar que se encuentra integrado por cuatro barras, cuatro uniones de perno y un eslabón esta impedido para moverse.
La movilidad de un mecanismo de cuatro barras se calcula de la siguiente manera:

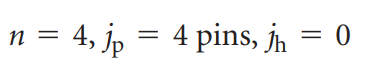

Mecanismos de 4 barras
Introducción
16/02
oscarrosete.com

oscarrosete.com

Como el mecanismo de cuatro barras tiene un grado de libertad, está restringido a un solo actuador o es totalmente operado por este.
El sistema del limpiador es activado por un motor eléctrico de corriente continua.
Mecanismos de 4 barras
Introducción
16/02
oscarrosete.com

oscarrosete.com
El eslabón impedido se elige como la bancada.
El eslabón pivote conectado al impulsor o a la fuente de potencia se conoce como eslabón de entrada.
El otro eslabón pivote, sujeto a la bancada, se designa como eslabón de salida o seguidor.
El acoplador o brazo conector "acopla" el movimiento de entrada con el del eslabón de salida.
Mecanismos de 4 barras
Introducción
16/02

oscarrosete.com

oscarrosete.com
Criterio de Grashof
La condición de Grashof es una relación muy simple que predice el comportamiento de rotación o rotabilidad de las inversiones de un eslabonamiento de cuatro barras basado sólo en las longitudes de los eslabones.
Mecanismos de 4 barras
16/02

oscarrosete.com

oscarrosete.com
Criterio de Grashof
La siguiente nomenclatura se utiliza para describir la longitud de los cuatro eslabones.
Mecanismos de 4 barras
s=longitud del eslabón más corto
l=longitud del eslabón más largo
p=longitud de uno de los eslabones de longitud intermedia
q=longitud del otro eslabón de longitud intermedia
16/02

oscarrosete.com

oscarrosete.com
Criterio de Grashof
Mecanismos de 4 barras
El teorema de Grashof establece que un mecanismo de cuatro barras tiene al menos un eslabón giratorio si:
s+l <= p+q
Los mecanismos que cumplen con esta condición son denominados mecanismos de Grashof
16/02
oscarrosete.com

oscarrosete.com
Criterio de Grashof
Mecanismos de 4 barras
Mecanismos de 4 barras clase I: s+l < p+q
Manivela - Balancín, Doble Manivela, Doble Balancín
Mecanismos de 4 barras clase III: s+l = p+q
Doble-Manivela o Manivela-Balancín.
Puntos de cambio/puntos muertos.
cuando todos los eslabones se vuelven colineales, se volverá indeterminado. “configuraciones inciertas”
16/02
oscarrosete.com

oscarrosete.com
Criterio de Grashof
Mecanismos de 4 barras
Mecanismos de 4 barras clase II, los tres eslabones que no están fijos solamente oscilarán si:
s+l>p+q
Los mecanismos que cumplen con esta condición no son denominados mecanismos de Grashof
Todas las inversiones obtendrán mecanismo de Doble balancín.
16/02
oscarrosete.com

oscarrosete.com
Categorías mecanismos/Criterio Grashof
Los mecanismos de cuatro barras caen en una de las cinco categorias listadas en la tabla


Mecanismos de 4 barras
16/02
bancada

oscarrosete.com

oscarrosete.com
Categorías mecanismos/Criterio Grashof

Mecanismos de 4 barras
16/02
bancada







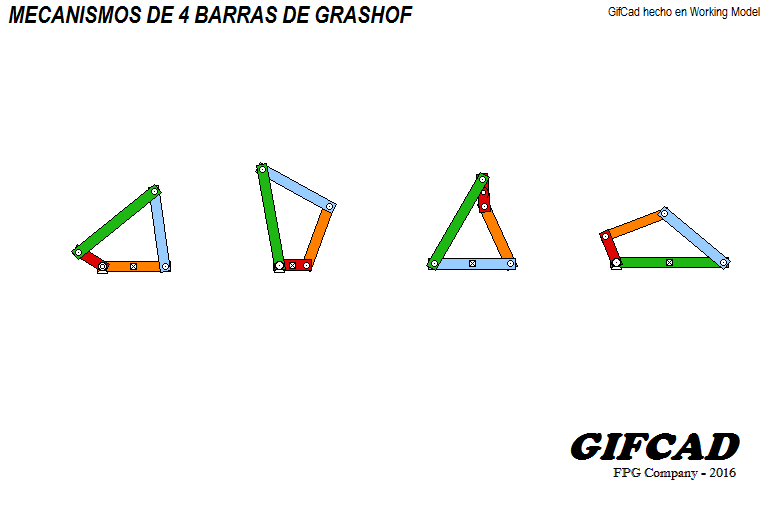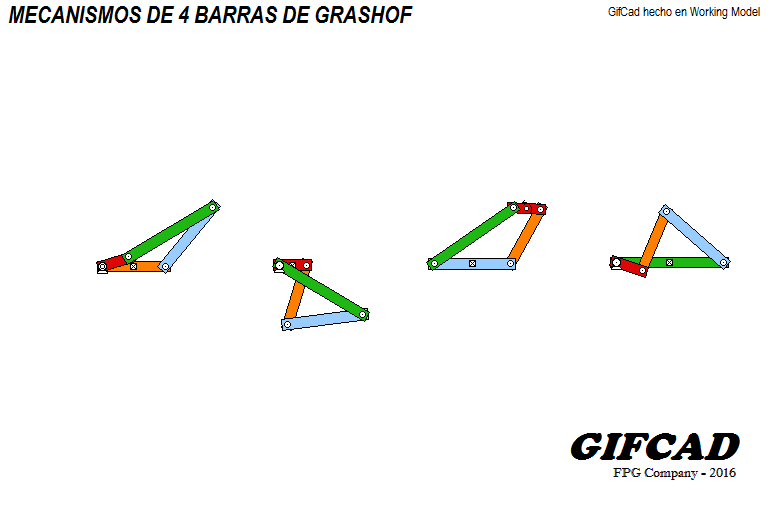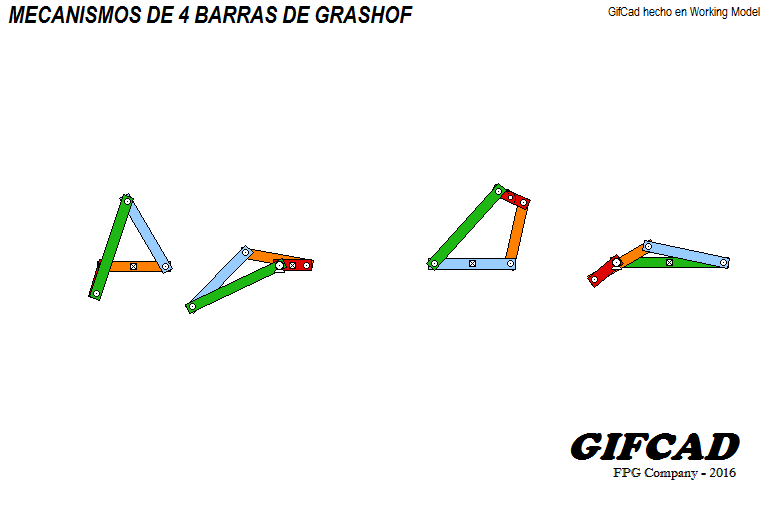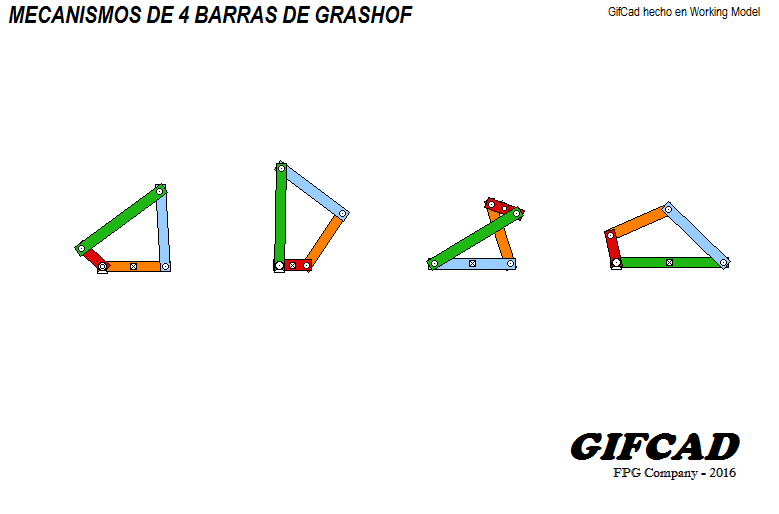
Las cinco categorías se muestran en los siguientes diagramas cinemáticos

Doble manivela
Doble balancín
Triple balancín
Doble manivela- Punto de cambio
Manivela-balancín
Categorías mecanismos/Criterio Grashof
Mecanismos de 4 barras
16/02
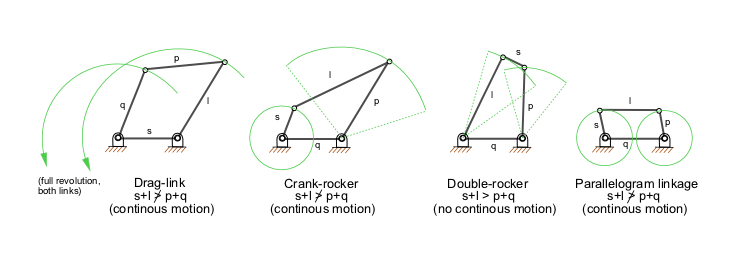
oscarrosete.com
oscarrosete.com

oscarrosete.com
Las cinco categorías se muestran en los siguientes diagramas cinemáticos
Categorías mecanismos/Criterio Grashof
Mecanismos de 4 barras
16/02

Manivela-balancín
Doble manivela
Doble balancín
oscarrosete.com

oscarrosete.com
Doble balancín
El eslabón mas corto, esta opuesto al configurado como la bancada. En esta configuración, ningún eslabón conectado a la bancada podrá completar una revolución. Solamente oscilara entre ciertos limites.
El acoplador si completa una revolución.


Mecanismos de 4 barras
16/02
oscarrosete.com

oscarrosete.com
Actividad Individual
Doble manivela
El eslabón mas corto del mecanismo de cuatro barras es configurado como la bancada.
Si uno de los eslabones pivote gira continuamente, el otro eslabón pivote también girará continuamente.


16/02
oscarrosete.com

oscarrosete.com
Actividad Individual
Punto de cambio
La suma de dos lados es la misma que la suma de los otros dos. El tipo mas familiar del mecanismo es el eslabonamiento que forma un paralelogramo. Los cuatro eslabones se traslaparan entre si


16/02
oscarrosete.com

oscarrosete.com
Actividad Individual
Triple balancin
No tiene eslabones que logren completar una revolución completa, de modo que los tres eslabones móviles se balancean


16/02
oscarrosete.com

oscarrosete.com
Actividad Individual
Manivela balancin
El eslabón mas corto gira continuamente, el eslabón de salida oscilara entre unos limites


16/02
oscarrosete.com
oscarrosete.com
Actividad Individual
Mecanismos de 4 barras
Para los mecanismos manivela balancín y doble balancín realizar los siguientes pasos:
- Identificar una aplicación.
- Realizar su propio mecanismo planar
- Realizar un diagrama cinemático de su mecanismo, identificar y clasificar los eslabones y juntas.
- Determinar la movilidad.
16/02

oscarrosete.com
oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos

Considérese los siguientes mecanismos y elabore su diagrama cinemático:





11/02


oscarrosete.com
oscarrosete.com
Actividad Individual
Ejemplos de diagramas cinemáticos

Considérese los siguientes mecanismos y elabore su diagrama cinemático:





11/02

Agenda
oscarrosete.com

oscarrosete.com
23/02
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com
oscarrosete.com
Actividad Individual
Mecanismos de 4 barras
Para los mecanismos manivela balancín y doble balancín realizar los siguientes pasos:
- Identificar una aplicación.
- Realizar su propio mecanismo planar
- Realizar un diagrama cinemático de su mecanismo, identificar y clasificar los eslabones y juntas.
- Determinar la movilidad.


23/02
oscarrosete.com
oscarrosete.com
oscarrosete.com
Actividad en equipo
En equipos, seleccionen un producto o sistema mecánico que de acuerdo a los conceptos vistos en el curso pueda ser considerado:
Mecanismo de cuatro barras
Máquina con mecanismo de 4 barras
- Identificar y clasificar las juntas que lo componen.
- Identificar y clasificar los eslabones que lo componen.
- Elaborar su diagrama cinemático
- Determinar su movilidad
- Clasificar de acuerdo al tipo y categorizar de acuerdo al criterio de Grashof.
Deberá generarse una presentación y subirse a actividad correspondiente de blackboard.
oscarrosete.com
23/02


oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Posición
En muchos mecanismos, el proposito del analisis es determinar unicamente la ubicacion de todos los eslabones conforme el (los) eslabon(es) impulsor(es) del mecanismo se mueve(n) hacia otra posición.

25/02

oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Posición
Para integrar el "clamp" a una maquina, es esencial entender el movimiento de los eslabones, asimismo debemos considerar las tolerancias de otros componentes en la maquinaria.

25/02

oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Posición
La posición se refiere a la ubicación de un objeto.
Estudiaremos la posición de puntos de interés y eslabones.
La posición de un punto sobre un mecanismo es la ubicación espacial de ese punto, que se define con un vector de posición, R, el cual se extiende de un origen de referencia a la ubicación del punto.

25/02
oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Posición
Al igual que todos los vectores, la posición en un plano se especifica con la distancia desde el origen (magnitud vectorial) y el angulo a partir de un eje de referencia (orientación).
Un vector bidimensional tiene dos atributos, los cuales pueden expresarse en coordenadas polares o cartesianas.

25/02

oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Desplazamiento
El desplazamiento de un punto es el cambio en su posición y se define como la distancia en línea recta entre la posición inicial y final de un punto que se ha movido en el marco de referencia.
Observe que el desplazamiento no es necesariamente el mismo que la longitud de la trayectoria que el punto pueda haber recorrido de su posición inicial a la final.

25/02
oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Desplazamiento
La fi gura muestra un punto en dos posiciones, A y B. La línea curva ilustra la trayectoria a lo largo de la cual viajó el punto.
El vector de posición RBA define el desplazamiento del punto B con respecto al punto A.

25/02

oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Desplazamiento
Se utilizará la notación R para denotar un vector de posición. Los vectores RA y RB definen, respectivamente, las posiciones absolutas de los puntos A y B con respecto a este marco de referencia global XY.

25/02



oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Desplazamiento
El vector RBA denota la diferencia de posición, o el desplazamiento, entre A y B. Éste se puede expresar como la ecuación de diferencia de posición

25/02



oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Desplazamiento
Esta expresión se lee: La posición de B con respecto a A es igual a la posición (absoluta) de B menos la posición (absoluta) de A, donde absoluta significa con respecto al origen del marco de referencia global.

25/02

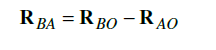

oscarrosete.com
oscarrosete.com
Análisis de Posición y desplazamiento
Posición angular de un eslabon
La posición angular de un eslabón tambien es una magnitud importante, se define como el ángulo que forma una línea entre dos puntos del eslabón con un eje de referencia.
En la figura, la linea MN queda sobre el eslabón 4. La posición angular del eslabón 4 se denota con θ4 (angulo entre eje x y la linea MN).
Medido en contra de las
manecillas del reloj(+).

25/02

oscarrosete.com
oscarrosete.com
Determinación de posición
Método gráfico
Los métodos gráficos para el análisis de posición y desplazamiento en mecanismos constituyen una excelente herramienta en el estudio cinemático, debido a que presentan un panorama muy claro de su funcionamiento.

25/02
oscarrosete.com
oscarrosete.com
Determinación de posición
Método gráfico
Para cualquier mecanismo con un GDL, tal como uno de cuatro barras, se requiere sólo un parámetro para definir por completo las posiciones de todos los eslabones. El parámetro usualmente elegido es el ángulo de eslabón de entrada.
El análisis gráfico de este problema es trivial y puede realizarse sólo con geometría de alta escuela.

25/02
oscarrosete.com
oscarrosete.com
Determinación de posición
Método gráfico
Si se dibuja el mecanismo de manera cuidadosa a escala, con una regla, compás y transportador en una posición particular (dado θ2), entonces sólo es necesario medir los ángulos de los eslabones 3 y 4 con el transportador.

25/02

oscarrosete.com
oscarrosete.com
Determinación de posición
Método gráfico
Obsérvese que todos los ángulos de los eslabones se miden con respecto a un eje X positivo.
Se creó una sistema de ejes xy local, paralelo al sistema XY global, en el punto A para medir θ3.

25/02

oscarrosete.com
oscarrosete.com
Determinación de posición
Método gráfico
El análisis de posición consiste en lo siguiente:
Dadas las longitudes de sus eslabones y la ubicación de sus pivotes, determine la posición de cada uno de los eslabones en función de la posición de entrada.

25/02
oscarrosete.com
oscarrosete.com
Determinación de posición
Procedimiento sugerido
- Establecer en una hoja de papel los nodos de todas las manivelas
- Trazar las trayectorias circulares de los nodos pertenecientes a las manivelas con el uso de sus radios de giro.
- Trazar las trayectorias de los nodos de las correderas paralelas al deslizamiento.

25/02
oscarrosete.com
oscarrosete.com
Determinación de posición
Procedimiento sugerido
- Establecer la posición del eslabón conocido.
- Para establecer la posición de las bielas, utilizar un compás cuya abertura sea el radio de la biela, posicionando el inicio del compás en la posición del eslabón conocido y luego trazando una circunferencia que intersecte la trayectoria del otro eslabón.

25/02
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02

Considerese el mecanismo de 4 barras, cuyas longitudes son
Determinar la posición de los eslabones si


oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02

Primero se establecen las posiciones de las articulaciones O2 y O4, para lo cual se utiliza l1 y θ1=0
Enseguida se trazan las circunferencias relacionadas con las trayectorias de las manivelas de entrada y salida.
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02

Al ubicarse en el nodo de entrada correspondiente a 110 de la posición de la manivela de entrada, se traza una circunferencia de la longitud I3=10cm.
La intersección indica dos soluciones existentes, conocidas como solución abierta y solución cerrada, se debe escoger la correcta al tener el conocimiento de la posición ultima anterior.
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02

Se selecciona la solución 1 y con esto se tiene la solución para la posición del mecanismo.
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02


la construcción de la solución gráfica de posición. Se dan las cuatro longitudes de los eslabones a,b,c,d y el ángulo θ2 del eslabón de entrada
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02


Primero, se dibuja la bancada (1) y el eslabón de entrada (2) a una escala conveniente, de modo que se corten en el origen O2 del sistema de coordenadas XY global con el eslabón 2 colocado en el ángulo de entrada θ2.
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02


Por conveniencia, el eslabón 1 se dibuja a lo largo del eje X. El compás se abre a la longitud a escala del eslabón 3 y se traza un arco de ese radio en torno al extremo del eslabón 2 (punto A).
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02


Se abre el compás a la longitud a escala del eslabón 4 y se traza un segundo arco en torno al extremo del eslabón 1 (punto O4).
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02


Estos dos arcos tendrán dos intersecciones en B y B′ que definen las dos soluciones al problema de posición de un mecanismo de cuatro barras, el cual puede ensamblarse
en dos configuraciones llamadas circuitos, designados como abierto y cruzado.
oscarrosete.com
oscarrosete.com
Determinación de posición
Ejemplo

25/02


Los ángulos de los eslabones 3 y 4 se miden con un transportador. Un circuito tiene los ángulos θ3 y θ4, el otro θ3' y θ4'. Una solución gráfica sólo es válida para el valor particular del ángulo de entrada utilizado.
oscarrosete.com
oscarrosete.com
Determinación de posición
Desventaja

25/02


Para cada análisis de posición adicional habrá que volver a dibujar por completo (tedioso al incrementar 1 o 2 grados)
oscarrosete.com
oscarrosete.com
Ejercicios de tarea
Identificar los ángulos θ3 y θ4 para el mecanismo mostrado en la imagen dado los siguientes datos:

03/02
- Eslabón 1:6, eslabón 2:2, eslabón 3:7, eslabón 4: 9 y θ2=30
- Eslabón 1:7, eslabón 2:9, eslabón 3:3, eslabón 4:8 y θ2=80


oscarrosete.com
oscarrosete.com
Determinación de posición
Procedimiento sugerido
03/02
oscarrosete.com
oscarrosete.com
Ejercicios de tarea
Identificar los ángulos θ3 y θ4 para el mecanismo mostrado en la imagen dado los siguientes datos:

09/02
- Eslabón 1:6, eslabón 2:2, eslabón 3:7, eslabón 4: 9 y θ2=30
- Eslabón 1:7, eslabón 2:9, eslabón 3:3, eslabón 4:8 y θ2=80


oscarrosete.com
oscarrosete.com
Método gráfico mecanismo manivela-biela-corredera
Considérese el mecanismo RRRP de la figura.
Si la manivela de entrada se encuentra posicionada a un ángulo de 40°, determinar la posición del nodo B de la corredera.
La barra 2 tiene una longitud de 3.0 cm y la barra 3 una de 7.76 cm.
09/02


oscarrosete.com
oscarrosete.com
Desplazamiento: Análisis gráfico
Para obtener una nueva configuración en un mecanismo, es necesario reubicar los eslabones en sus nuevas posiciones y considerar las trayectorias restringidas de los eslabones unidos a las bancadas.
09/02


oscarrosete.com
oscarrosete.com
Desplazamiento: Análisis gráfico
En la figura se muestra un diagrama cinemático impulsado pro el movimiento del eslabón 2. Reposicione gráficamente los eslabones del mecanismo, conforme el eslabón 2 se desplaza 30 en sentido anti-horario.
Determine el desplazamiento angular resultante del eslabón 4 y el desplazamiento lineal del punto E.
09/02


oscarrosete.com
oscarrosete.com
Desplazamiento: Análisis gráfico
En la figura se muestra un diagrama cinemático impulsado pro el movimiento del eslabón 2. Reposicione gráficamente los eslabones del mecanismo, conforme el eslabón 2 se desplaza 30 en sentido anti-horario. Determine el desplazamiento angular resultante del eslabón 4 y el desplazamiento lineal del punto E.
09/02


oscarrosete.com
oscarrosete.com
Tarea Individual-Ejercicio 1
Cuando se requieren grandes fuerzas de corte, se usan con frecuencia unas tijeras de palanca de hojalatero como las mostradas en la figura. Con el uso del mango superior como bancada, reposicione gráficamente las componentes de las tijeras cuando la mordaza se abre 15. Determine el desplazamiento resultante del mango inferior.
09/02



oscarrosete.com
oscarrosete.com
Tarea Individual-Ejercicio 2
El mecanismo que se representa en la figura corresponde a un proceso de corte; en este mecanismo, el pistón de corte contiene una cuchilla que efectúa el trabajo de corte. Para las dimensiones dadas y la posición de la manivela, determina la posición vertical de la corredera mediante el método gráfico.
09/02


Agenda
oscarrosete.com

oscarrosete.com
16/03
1.1 Conceptos básicos.
1.2 Transmisión del movimiento.
1.3 Mecanismos de 4 barras.
1.4 Ley de Grashoff.
1.5 Velocidad angular de miembros en contacto directo.
1.6 Aplicaciones del mecanismo de 4 barras.
1.7 Análisis de posición de mecanismos
Unidad 1: Introducción al estudio de los Mecanismos
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Introducción

oscarrosete.com
oscarrosete.com
El análisis de velocidad y aceleración en mecanismos articulados requiere un estudio detallado, muy diferente al que se hace con las partículas

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Consideraciones

oscarrosete.com
oscarrosete.com
- Las ecuaciones cinemáticas son ecuaciones vectoriales. Por esta razón requieren una solución vectorial gráfica y(o) analítica.
- Existen diferentes tipos de velocidades y aceleraciones. Por ejemplo, velocidades y aceleraciones angulares de los eslabones, velocidades y aceleraciones tangenciales en los nodos y(o) uniones y velocidades rectilíneas en las correderas, entre otras.

16/03
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Consideraciones

oscarrosete.com
oscarrosete.com
- Los métodos gráficos permiten solucionar ecuaciones de velocidad y aceleración mediante trazos vectoriales, en especial para el cálculo en un instante dado del mecanismo.
- No obstante, lo anterior no aplica para los métodos analíticos, en los que es posible establecer ecuaciones representativas de velocidad y aceleración en cualquier instante, obteniendo resultados más exactos en comparación con los métodos gráficos.

16/03
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Conceptos básicos

oscarrosete.com
oscarrosete.com
Velocidad se define como la magnitud del cambio de la posición con respecto al tiempo.
Aceleración es el cambio en la magnitud de la velocidad respecto al tiempo.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
El análisis de velocidad en los elementos de un mecanismo radica principalmente en comprender la relación vectorial que existe entre la velocidad de rotación en un eslabón y la velocidad tangencial en cada uno de sus nodos de articulación.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
Para dejar en claro lo anterior, considérese el mecanismo manivela-corredera de la figura, el cual dispone de una manivela 2, con un movimiento de rotación alrededor del nodo O2.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
Por su parte, el nodo A transmite el movimiento del eslabón 2 al eslabón 3 y tiene una trayectoria circular, mientras que el nodo B transmite el movimiento del eslabón 3 al 4, al tiempo que, debido a que forma parte de la corredera 4, tiene una trayectoria rectilínea.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad

oscarrosete.com
oscarrosete.com
Como primer paso del análisis cinemático de mecanismos se establecen las ecuaciones de velocidad aislando cada elemento, en las cuales el cambio de posición se expresa como un vector desplazamiento Δr

16/03



oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad angular

oscarrosete.com
oscarrosete.com
La velocidad angular, o de rotación, puede presentarse en los eslabones con movimiento de rotación alrededor de un punto.
La velocidad angular promedio e instantánea se define como:

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad tangencial

oscarrosete.com
oscarrosete.com
La velocidad tangencial se encuentra en los nodos de un eslabón y es tangente a la trayectoria generada por el nodo durante el movimiento.

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad

oscarrosete.com
oscarrosete.com
Cuando un eslabón tiene movimiento de rotación, como en el caso de la figura a), cada nodo del eslabón experimenta un desplazamiento lineal, que se denota por ΔrA, el cual, después de ser dividido por el lapso de tiempo, proporciona la velocidad de desplazamiento, o velocidad tangencial (VT ):

16/03
Velocidad tangencial


oscarrosete.com
oscarrosete.com
Análisis de velocidad
Relación entre velocidad tangencial y angular

oscarrosete.com
oscarrosete.com
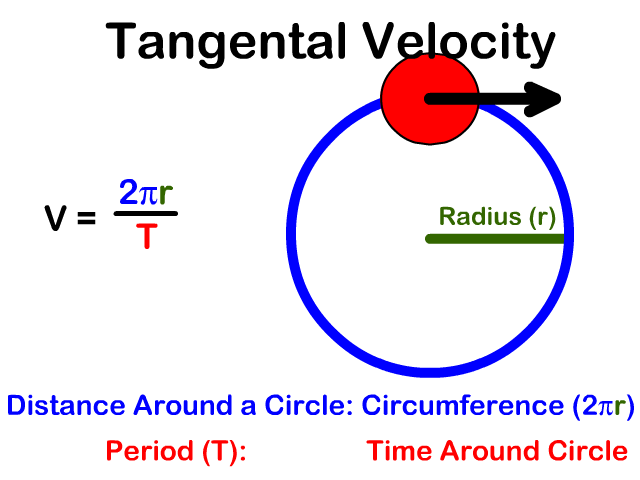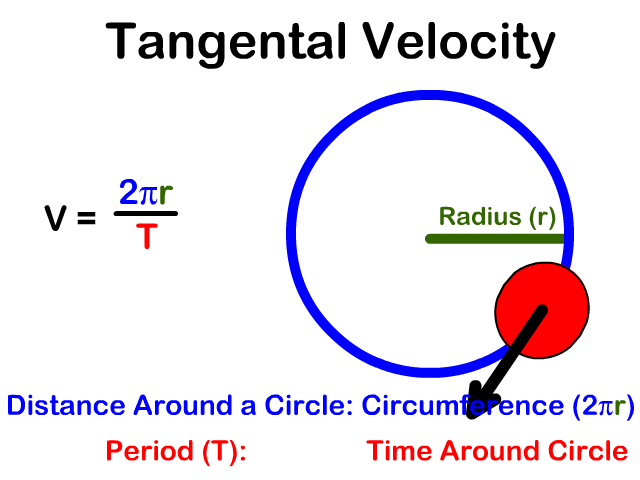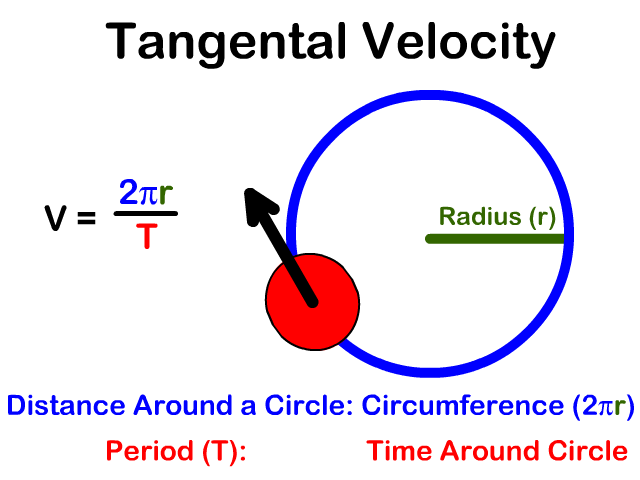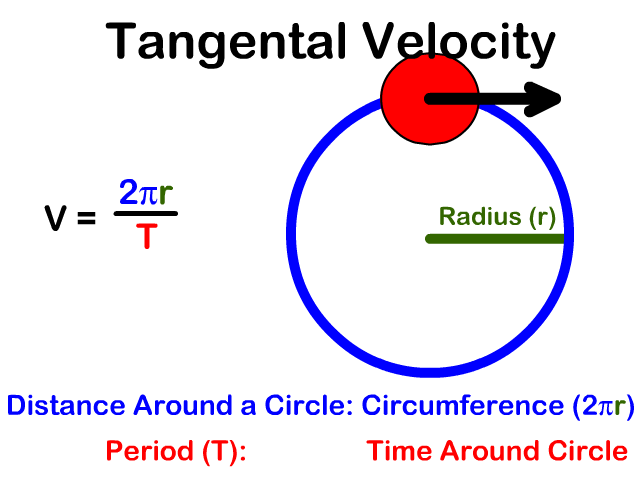
En los eslabones que tienen movimiento de rotación existe una relación entre la velocidad angular del eslabón (ω) y la velocidad lineal de algún nodo del eslabón (V), conocida como velocidad tangencial. Si la longitud de arco en una circunferencia es s=rθ, entonces para pequeños desplazamientos del nodo A de la manivela se tiene ds=rAdθ; por tanto:

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad

oscarrosete.com
oscarrosete.com
Así, se establece una relación entre la magnitud de la velocidad lineal de un nodo VTA con la velocidad de rotación (ω) y el radio de giro (rA), siempre y cuando no cambie la magnitud del radio de giro.

16/03


Relación entre velocidad tangencial y angular
oscarrosete.com
oscarrosete.com
Análisis de velocidad

oscarrosete.com
oscarrosete.com
Tanto la posición de un mecanismo como la velocidad tangencial de uno de sus nodos son cantidades vectoriales, y como vector la velocidad tangencial es perpendicular al radio de giro, cuyo sentido depende del movimiento del eslabón.

16/03

Relación entre velocidad tangencial y angular
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad rectilínea

oscarrosete.com
oscarrosete.com
Considérese ahora el caso de un sólido rígido que tiene un movimiento de translación rectilínea, como el de la figura. Cada partícula de un sólido rígido tiene los mismos desplazamientos; además, debido a que las trayectorias entre dos nodos del mismo eslabón son siempre paralelas, la velocidad en cada partícula siempre es lineal e idéntica, la cual se conoce como velocidad rectilínea o lineal VL y se define como:

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad rectilínea

oscarrosete.com
oscarrosete.com
Vectorialmente, la dirección de la velocidad rectilínea VL es paralela al movimiento de la corredera en el sentido de esta, como se muestra en la figura

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Tanto la velocidad tangencial como la velocidad rectilínea se conocen como velocidades absolutas, ya que ambas se miden desde un marco de referencia fijo.

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Asimismo, existe otro tipo de velocidad, conocida como velocidad relativa, vector que se mide tomando como origen un nodo del sólido rígido que se encuentra en movimiento.
Un ejemplo de estas velocidades lo constituyen las bielas, debido a que en este eslabón todos sus nodos están en movimiento.

16/03
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Para el análisis de velocidad relativa considérese un observador que está situado en el nodo A de un sólido rígido, el cual desea determinar la velocidad de otro nodo, al que se denomina nodo B.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Con base en lo anterior, ¿cómo es el desplazamiento del nodo B visto desde A, es decir, (ΔrB/A)? Entonces, para hallar la velocidad se fija el nodo A y se trazan ambas posiciones relativas (ΔrB1/A1 y ΔrB2 /A2), como se muestra en la figura.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
De lo anterior puede deducirse que, en términos generales, las trayectorias de los nodos A y B son des- conocidas, ya que dependen del eslabón al cual habrán de articularse.

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Sin embargo, independientemente de las trayectorias absolutas de A y B, la trayectoria relativa de B vista desde A es siempre conocida y circular, por lo que la velocidad relativa (VB/A) puede determinarse mediante la ecuación:

16/03


oscarrosete.com
oscarrosete.com
Análisis de velocidad
Velocidad relativa

oscarrosete.com
oscarrosete.com
Como la trayectoria relativa de dos puntos de una misma barra siempre es circular, entonces la dirección de la velocidad relativa es perpendicular al radio de giro como dirección.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Método del polígono de velocidad

oscarrosete.com
oscarrosete.com
Al considerar dos puntos p y q de cualquier eslabón rígido en un mecanismo, la ecuación de velocidad entre dichos puntos quedará determinada de la siguiente manera:

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Método del polígono de velocidad

oscarrosete.com
oscarrosete.com
Si la ecuación fuera algebraica, entonces se requerirían dos datos (de tres) para su solución, pero como es una ecuación vectorial que posee magnitud y dirección por vector, entonces se requiere de cuatro datos (de seis) para su solución.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Método del polígono de velocidad

oscarrosete.com
oscarrosete.com
Las velocidades Vp y Vq se conocen como velocidades absolutas, y su magnitud y dirección dependen de los eslabones a los que se encuentran articulados.
Por otra parte, la velocidad relativa (Vp/q) puede calcularse mediante la expresión Vp/q=(ωp/q)(rp/q), ya que siempre es de trayectoria circular y, por tanto, perpendicular al radio de giro rp/q.

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
1. Identificar el dato conocido de velocidad, ya sea velocidad angular (por parte de un eslabón) o velocidad tangencial (por parte de un nodo).
2. Si se conoce la velocidad angular de un eslabón, establecer ecuaciones de puntos de la misma barra p y q que pertenezcan al mismo eslabón mediante:

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
3. La ecuación vectorial tendrá solución si se tienen como máximo dos incógnitas. Si se tienen más incógnitas, deberá establecerse otra ecuación que relacione el punto de interés con otro nodo del eslabón, del cual por lo menos se conozca su trayectoria.
Las incógnitas pueden ser la magnitud y(o) la dirección por cada vector; si la trayectoria del nodo es circular o rectilínea, entonces se dice que es conocida; de ser circular, será perpendicular al radio de giro; y si es rectilínea, será paralela a la línea de desplazamiento.

16/03
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
4. Se tiene un caso específico cuando se plantea la ecuación de velocidad de dos puntos de la misma barra en una manivela, ya que la velocidad en uno de sus nodos (Vp) es igual a la velocidad relativa del nodo vista desde el pivote Ox (Vp/Ox), el cual al estar siempre fijo es de magnitud nula:

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com
5. Resolver las ecuaciones vectoriales en el orden permitido. Una ecuación vectorial contiene vectores representados por magnitud y dirección, y tendrá solución solo si se tienen dos incógnitas.
Para la solución de la ecuación vectorial se pueden presentar dos opciones, como se muestra en la siguiente tabla

16/03
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com

16/03
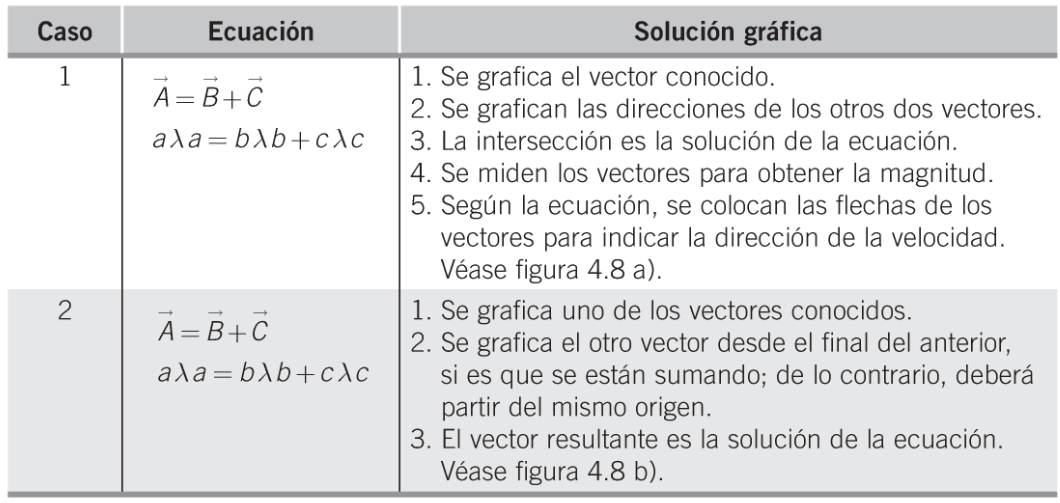
oscarrosete.com
oscarrosete.com
Análisis de velocidad
Metodología

oscarrosete.com
oscarrosete.com

16/03

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Ejemplo

oscarrosete.com
oscarrosete.com
16/03
El mecanismo de la figura representa el diagrama cinemático de un mecanismo manivela-oscilador. La manivela 2 se mueve a una velocidad constante de 5 rad/s, cmr (en sentido contrario al movimiento de las manecillas del reloj).

oscarrosete.com
oscarrosete.com
Análisis de velocidad
Ejemplo
oscarrosete.com
oscarrosete.com
16/03
Determinar la velocidad del centro de gravedad G de la biela 3 mediante el uso del método gráfico del polígono de velocidad.

oscarrosete.com
oscarrosete.com
Ejercicio de tarea
oscarrosete.com
oscarrosete.com
16/03
La barra AB del mecanismo de cuatro articulaciones de la figura gira con una velocidad angular w1 de 9 rad/s en sentido antihorario. Determine las velocidades angulares w2 y w3 de las barras BC y CD, en la posición mostrada