Gamma ray production in sources with relativistic outflows and complex environments

Yukawa Institute, 京都市, 14th February 2017

V. M. DE LA CITA

Outline of the talk

  • gamma-ray sources with relativistic outflows

  • Methods: coupling hydrodynamics and NT calculation

  • star-jet interactions in active galactic nuclei

  • pulsar wind interacting with a clumpy stellar wind

  • clumpy wind-jet interacions in high-mass microquasars

gamma-ray astronomy

Gamma rays allow us to study non-thermal (NT) processes of emission in astronomical sources, given that at these energies there is no contamination of thermal radiation.

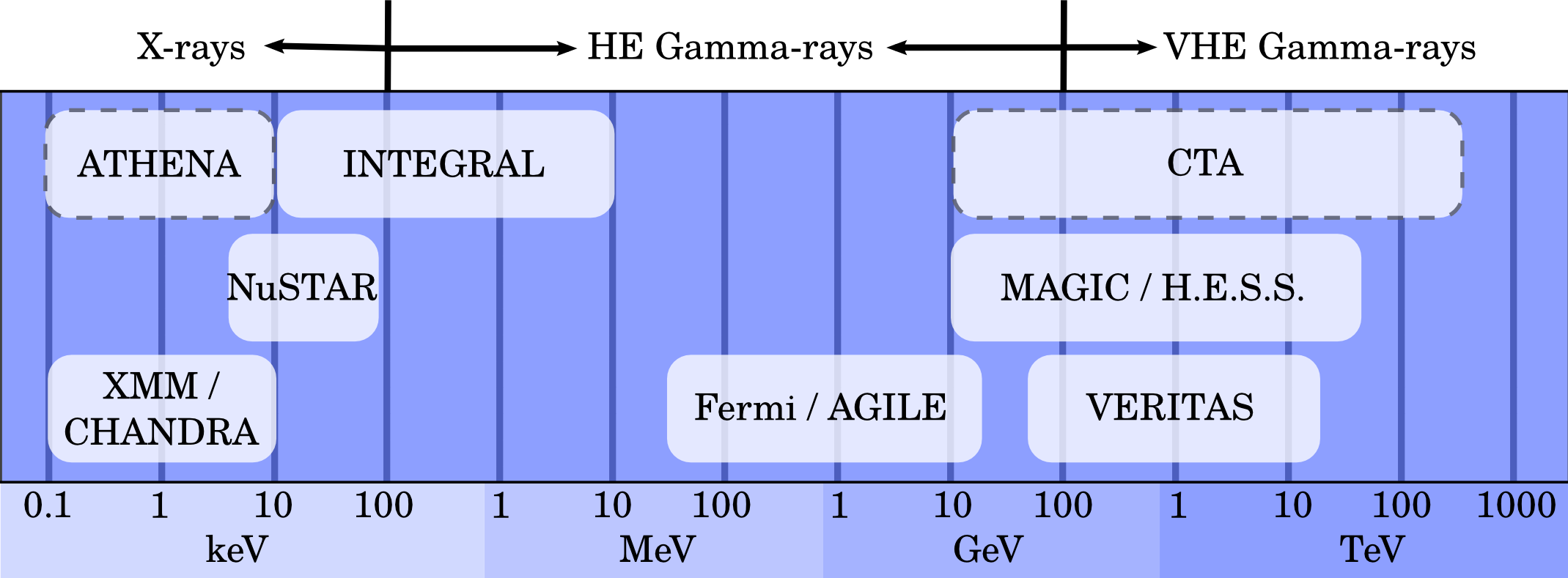
Space satellites like Fermi or AGILE and ground-based Cherenkov array telescopes like MAGIC, H.E.S.S. or HAWC are the current observational tools in gamma rays.

Gamma-ray sources with relativistic outflows

Active galactic nuclei

Credit: Seeds (1997)

NT processes are expected to play an important role in several sites inside a galaxy containing an AGN, such as the accretion disk, the jet itself or within its termination shock.

Gamma-ray sources with relativistic outflows

GAMMA-ray binaries and microquasars

Credit: Mirabel (2006)

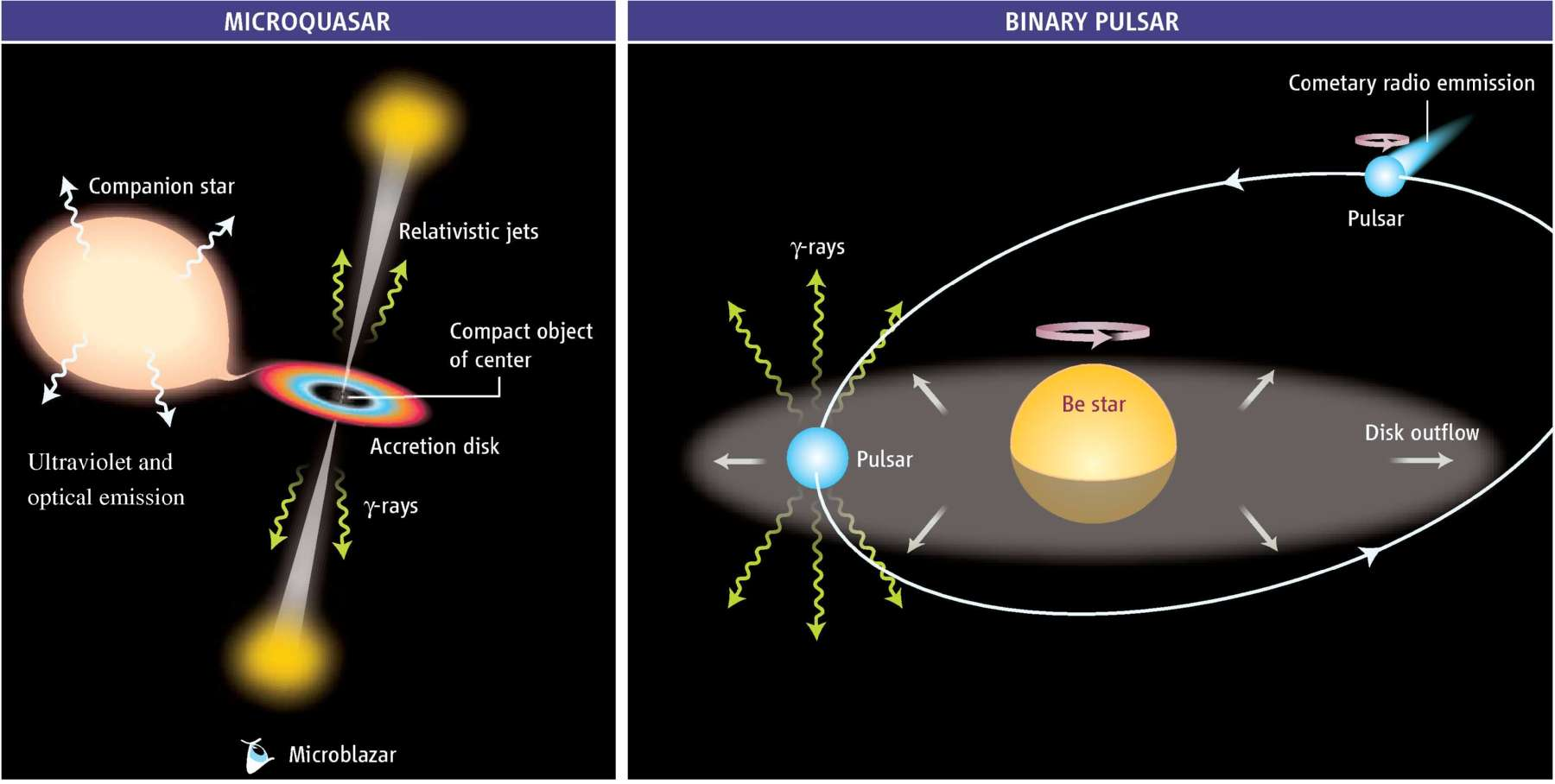
Gamma-ray binaries are formed by a compact object (BH or NS) and a companion massive star. The radiation production site is related with the interaction between the powerful star winds and the compact object.

Microquasars are a special kind of binary, also composed by a compact object and star, but in this case the compact object accretes material from the star. This may lead to the formation of two jets, observable from radio to X-rays and, in some cases, gamma-rays.

Gamma-ray sources with relativistic outflows

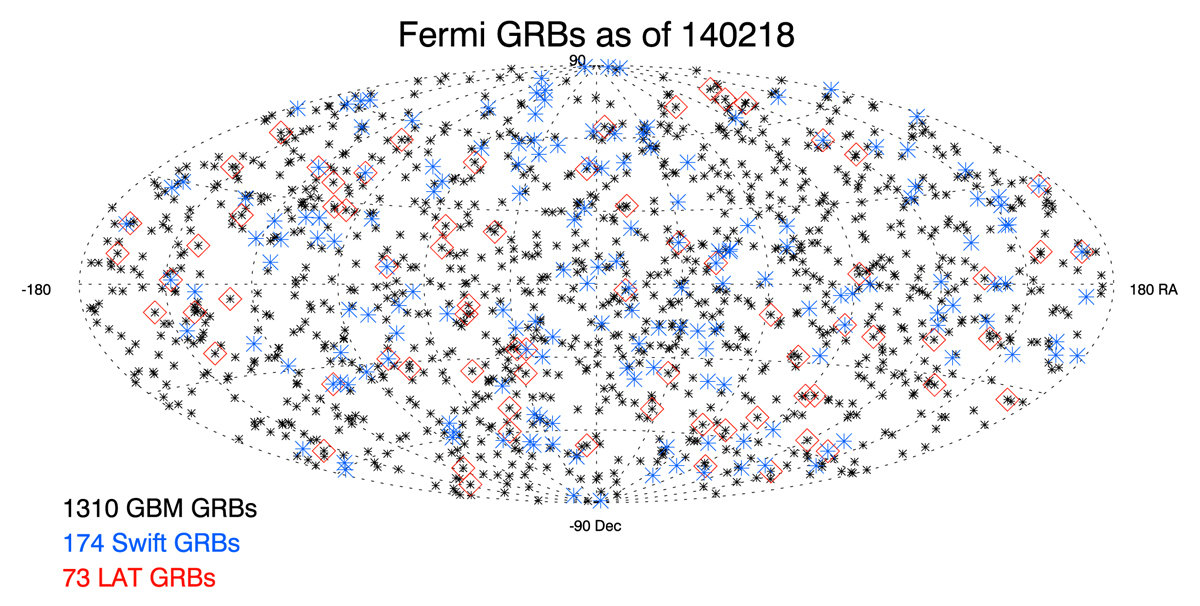
GAMMA-ray bursts

Credit: Gruber et al. (2014) and Kienlin et al. (2014)

Not covered in this work

Gamma-ray sources with relativistic outflows

Complex environments

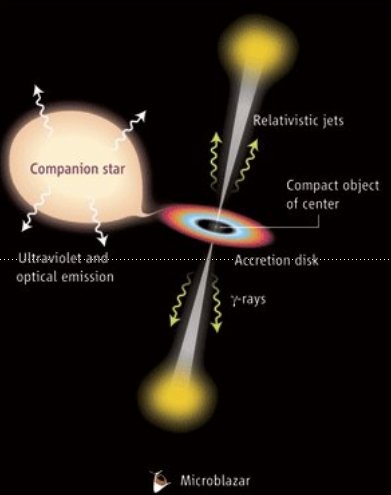
​​Credit: F. Mirabel

Outline of the talk

  • gamma-ray sources with relativistic outflows

  • Methods: coupling hydrodynamics and NT calculation

  • star-jet interactions in active galactic nuclei

  • pulsar wind interacting with a clumpy stellar wind

  • clumpy wind-jet interacions in high-mass microquasars

Coupling Hydrodynamics And NT computation

Outline

  1. Perform relativistic hydrodynamic simulations of the system. In our case, 2D axisymmetric simulations.
  2. Extract the streamlines of the simulated fluid.
  3. Compute the injection of NT particles, assuming a given acceleration efficiency.
  4. Let the particles evolve inside the fluid, until a steady-state is reached.
  5. Compute the NT emission. We focused on the most efficient channels in our systems: inverse Compton (IC) and synchrotron emission.
  6. Plot SEDs and maps of the results.

This was done by our collaborators. I'm not an expert on hydro!

Coupling Hydrodynamics And NT computation

Hydrodynamic setup and streamline calculation

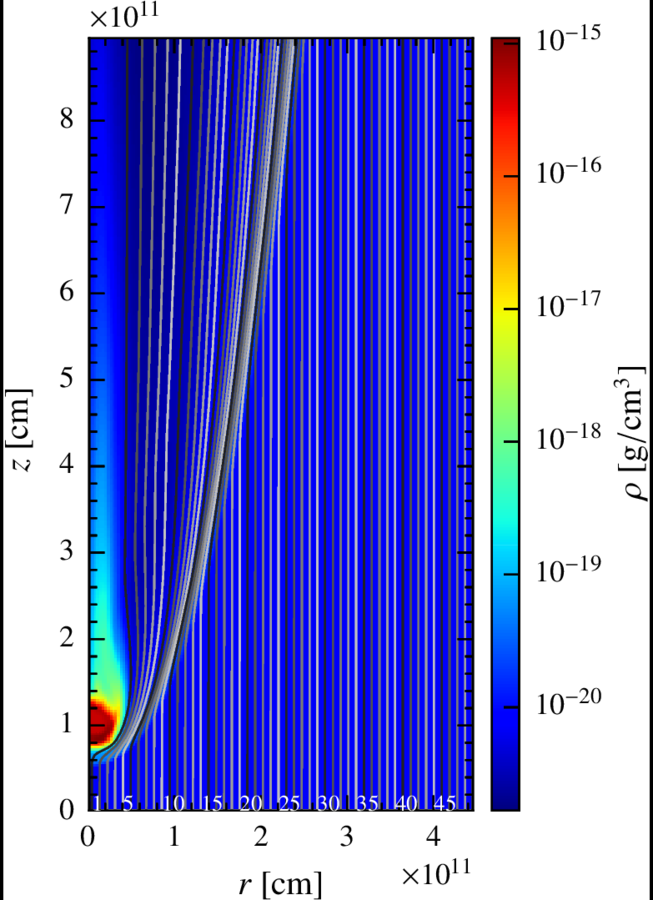
We perform relativistic hydrodynamic simulations in 2D taking advantage of the axisymmetry of our systems.

In this simulations the magnetic field was not included.

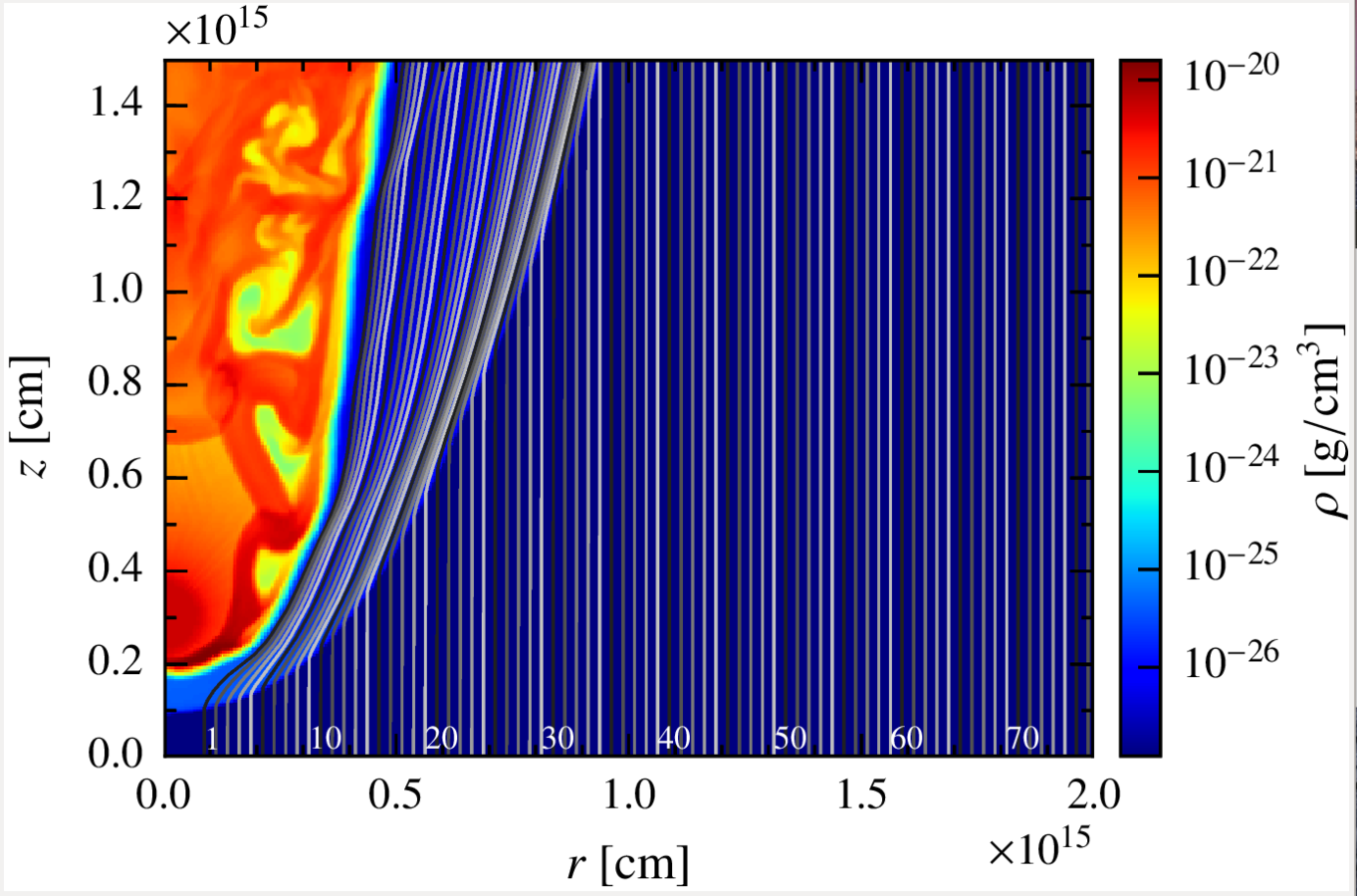
Later we define a set of fluid elements at the bottom of our grid and we draw the trajectories they follow (streamlines).

Coupling Hydrodynamics And NT computation

Hydrodynamic setup and streamline calculation

Although the RHD simulation is 2D, we take this information and scramble the different lines around the z axis, giving each cell a random azimuthal angle psi, so the result is more similar to the 3D real scenario.

Coupling Hydrodynamics And NT computation

We inject non-thermal particles when a shock takes place:

Internal energy goes up

and

fluid velocity goes down

Where and how do we inject non-thermal particles

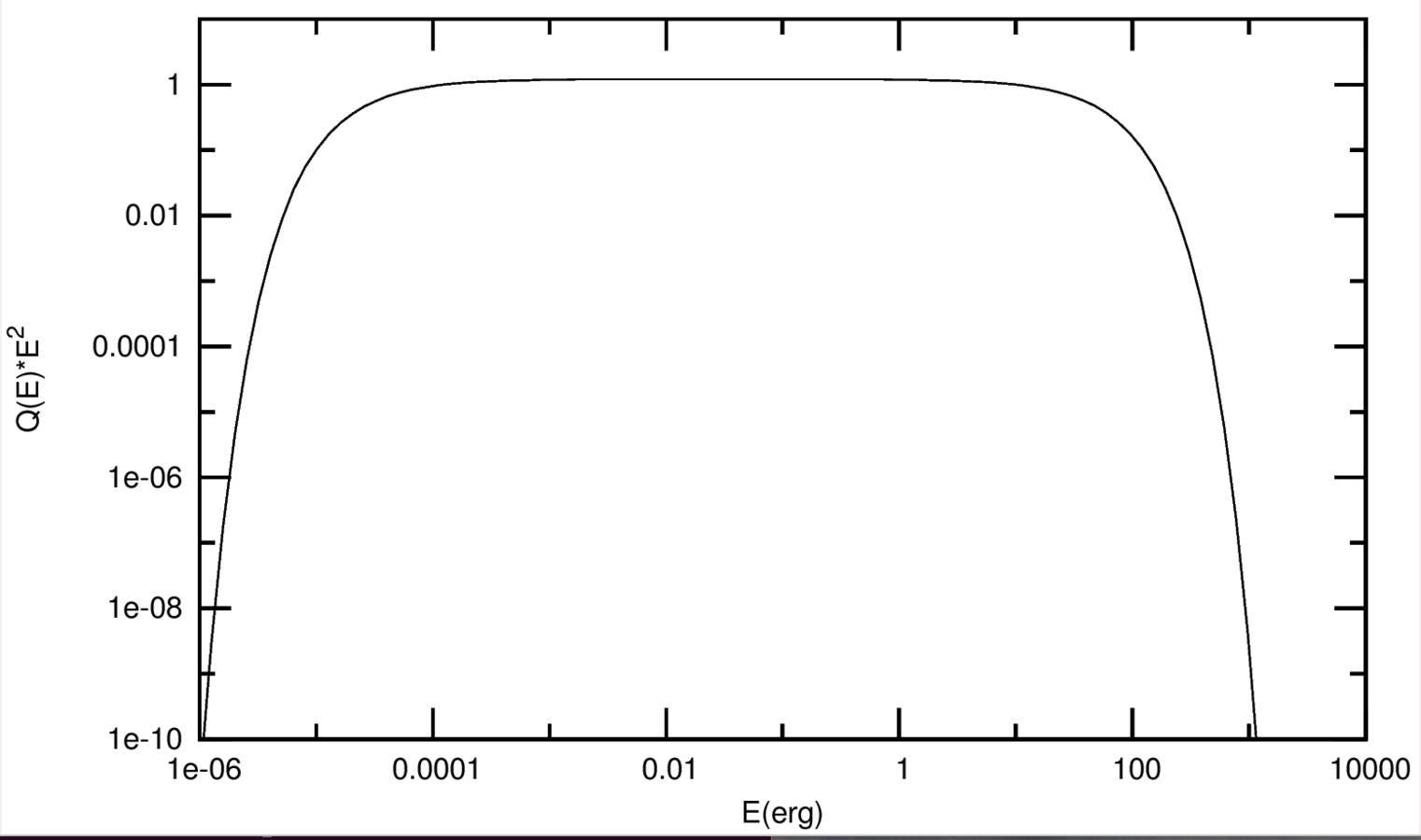
Q(E) \propto E^{-2} \times (e^{-E_{min}/E})^5 \times e^{-E/E_{max}}
Q(E)∝E−2×(e−Emin/E)5×e−E/EmaxQ(E) \propto E^{-2} \times (e^{-E_{min}/E})^5 \times e^{-E/E_{max}}

A fraction of the generated internal energy per second in a given cell is transferred to NT particles.

Coupling Hydrodynamics And NT computation

Particle evolution and NT radiation

  1. We let the particles evolve until they reach a steady state so we can consider the medium stationary, in other words, every loss time (e.g. synchrotron) or cell-crossing time is much shorter than the dynamical time on large scales.
  2. All the particle evolution and radiation computations are done in the (relativistic) frame of the fluid, so every relevant quantity has to be transformed, including the angles between fluid, gamma photons and target photons velocities.
  3. Once we have the electron distribution, we compute the inverse Compton (IC) and synchrotron radiation, taking into account  Doppler boosting.
\delta = 1/\Gamma(1-\beta\cos{\theta_\text{obs}})
δ=1/Γ(1−βcosθobs)\delta = 1/\Gamma(1-\beta\cos{\theta_\text{obs}})
\epsilon L(\epsilon)= \delta^4\epsilon'L(\epsilon')
ϵL(ϵ)=δ4ϵ′L(ϵ′)\epsilon L(\epsilon)= \delta^4\epsilon'L(\epsilon')

where

Coupling Hydrodynamics And NT computation

Outline of the talk

  • gamma-ray sources with relativistic outflows

  • Methods: coupling hydrodynamics and NT calculation

  • star-jet interactions in active galactic nuclei

  • pulsar wind interacting with a clumpy stellar wind

  • clumpy wind-jet interacions in high-mass microquasars

Star-jet interactions: a tale of two winds

  • 70's:  Blandford & König 79 propose stars/clouds can form shocks inside AGN jets
  • 80's: Several authors (Frölik et al. 89, Rees 87, Penston 88) explore the possibility of the BLR being the interactive cloud.
  • 90's: Analytical (Komissarov 94) and numerical (Bowman et al. 96) studies of the dynamical impact of stars on AGN jets. 
  • 00's: Hubbard & Blackman 06, Perucho et al. 14 - disruption of the jet by stars.

Impact on the jet dynamics

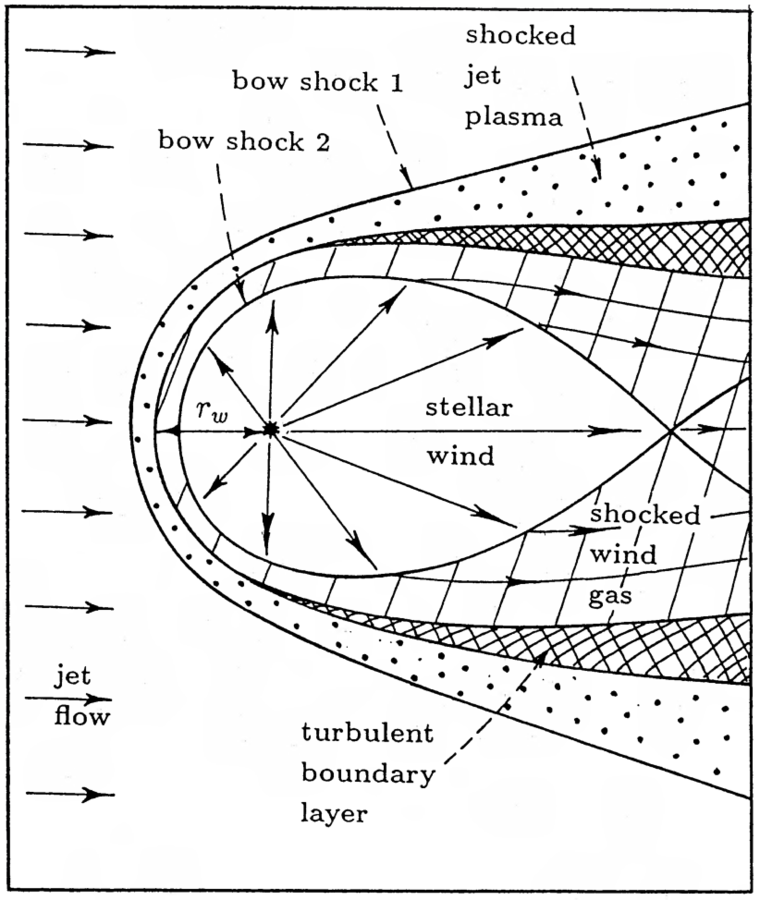
Komissarov 94

Star-jet interactions: a tale of two winds

  • 90's: Bednarek & Protheroe 97 first studied the possibility
  • S. XXI: Several authors have explored the blazar, non-blazar, transient and persistent high energy emission (Barkov, Khangulyan, Bosch-Ramón, Araudo)
  • Even observational evidence could exist (Hardcastle et al. 2003, Müller et al. 2014) 

Gamma-ray emission

Inner parsec of Centaurus A
Müller, C. et al. 2014
Bednarek & Protheroe 1997; Barkov et al. 2010, 2012; Khangulyan et al. 2013; 
Bosch-Ramon et al. 2012; Araudo et al. 2010,2013; Bosch-Ramon 2015; 
Bednarek & Banasinski 2015, this work.

physical scenario

The impact of stars and its atmospheres on AGN jets has been studied previously by other authors.

A number of problems must be addressed: the type of star populations, the impact of the stars in the jet dynamics...

We perform hydrodinamic simulations ot the regions close to the star, and then we compute its non-thermal emission.

physical scenario. A single star 

Inner parsec of Centaurus A
Müller, C. et al. 2014

10 pc

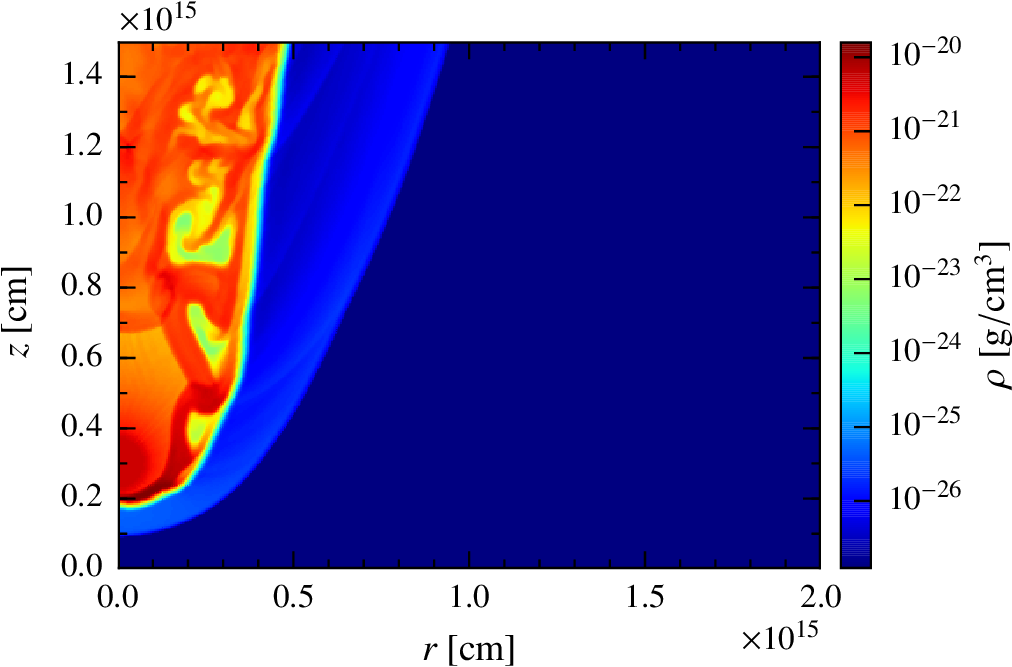
We fix our coordinate system with the z axis in the line connecting the base of the jet and the star. The shock is formed where the ram pressures of the two winds are balanced.

Our workframe

\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
v⃗stellar wind=2000 km s−1\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
\dot{M}_\star = 10^{-9} M_\odot \text{yr}^{-1}
M˙⋆=10−9M⊙yr−1\dot{M}_\star = 10^{-9} M_\odot \text{yr}^{-1}

The stellar wind is uniform with the thrust of a high mass star with moderate mass-loss rate (the corresponding thrust also typical for red giants) with the following data:

The jet has a luminosity of:

and a wind Lorentz factor of:

L_\text{jet} \sim 10^{44}\text{ erg s}^{-1}
Ljet∼1044 erg s−1L_\text{jet} \sim 10^{44}\text{ erg s}^{-1}
\Gamma = 10
Γ=10\Gamma = 10

for a 1 pc radius

Going into details. hidrodynamic setup.

The fluid is divided in 77 lines with 200 cells each, describing an axisymmetric 2D space of:

r\in[0,2\times10^{15}\text{ cm}]
r∈[0,2×1015 cm]r\in[0,2\times10^{15}\text{ cm}]
z\in[0,1.5\times10^{15}\text{ cm}]
z∈[0,1.5×1015 cm]z\in[0,1.5\times10^{15}\text{ cm}]
z_\star = 3\times 10^{14} \text{ cm}
z⋆=3×1014 cmz_\star = 3\times 10^{14} \text{ cm}

Going into details. Physical assumptions.

Magnetic field perpendicular to the fluid line

\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0cv)
B0′24π=χB(ρ0h0cv)\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0cv)
\chi_B = 10^{-4}, 0.1
χB=10−4,0.1\chi_B = 10^{-4}, 0.1

Definition of the magnetic field at the beginning of the line:

(Low, high magnetic field)

Fraction of matter energy flux that goes to magnetic energy (Poynting flux)

Photon field:

T_{\star} = 3\times 10^3 \text{ K}
T⋆=3×103 KT_{\star} = 3\times 10^3 \text{ K}
L_{\star} = 3\times 10^{36} \text{erg s}^{-1}
L⋆=3×1036erg s−1L_{\star} = 3\times 10^{36} \text{erg s}^{-1}

injection of non-thermal particles in the fluid:

A fraction of the generated internal energy per second in a given cell (at the shocks) is transferred to non-thermal particles.

\chi = 0.1
χ=0.1\chi = 0.1

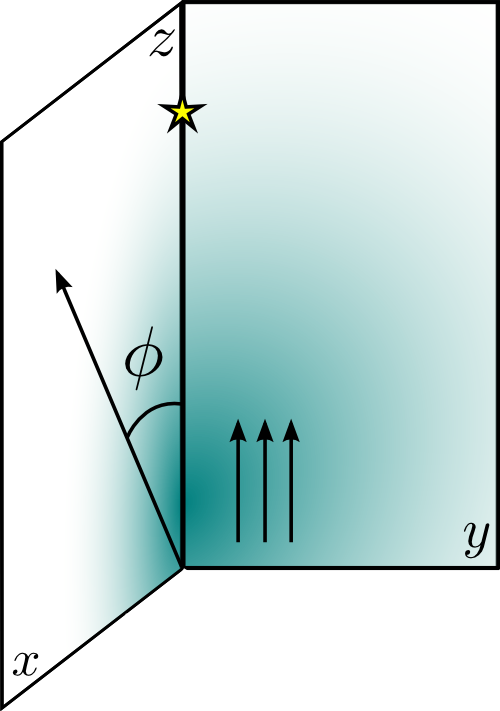
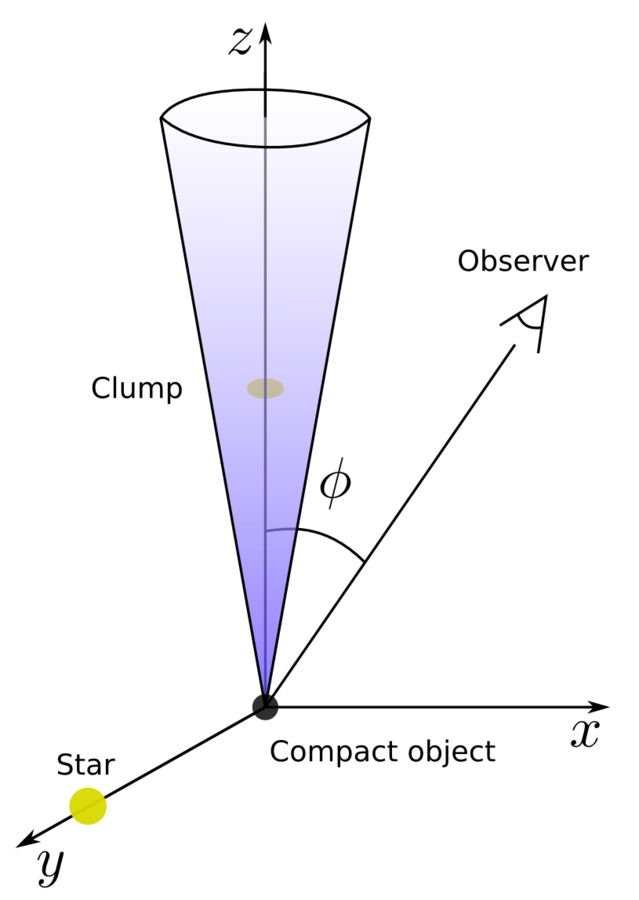
Going into details. Observer angle.

To sample a wide range of possibilities, we take four angles: 0º (with the jet bulk velocity pointing at the observer),  45º, 90º (when the observer is placed on the z axis) and 135º.

The observer will be placed beyond the star forming an angle phi with the vertical axis. 

Star

Jet thrust

\phi = 0^\circ, 45^\circ, 90^\circ, 135^\circ
ϕ=0∘,45∘,90∘,135∘\phi = 0^\circ, 45^\circ, 90^\circ, 135^\circ

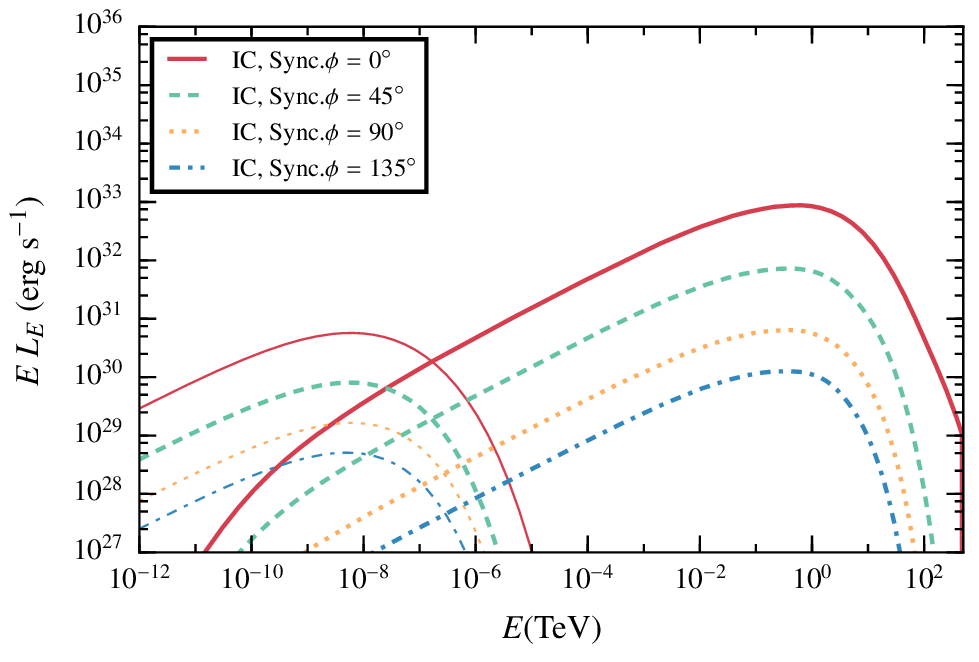
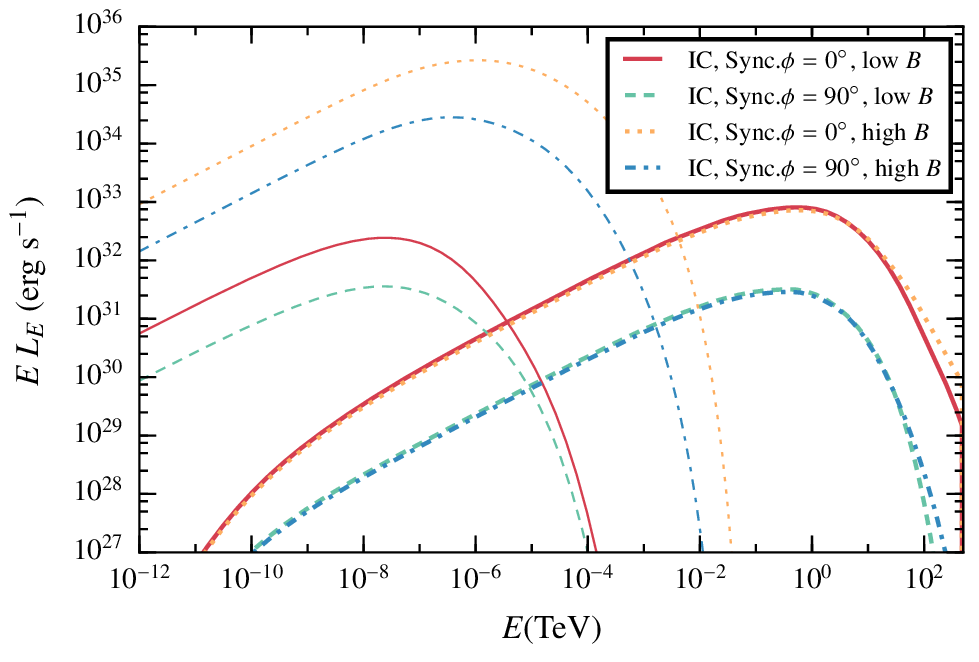
Results. Low magnetic field, steady state.

In the case of a low magnetic field, the IC radiation dominates the spectrum.

The difference between the four angles come from the doppler boosting, more important for smaller angles given that most of the cells have a strong         z- component of the  velocity

\chi_B = 10^{-4}
χB=10−4\chi_B = 10^{-4}

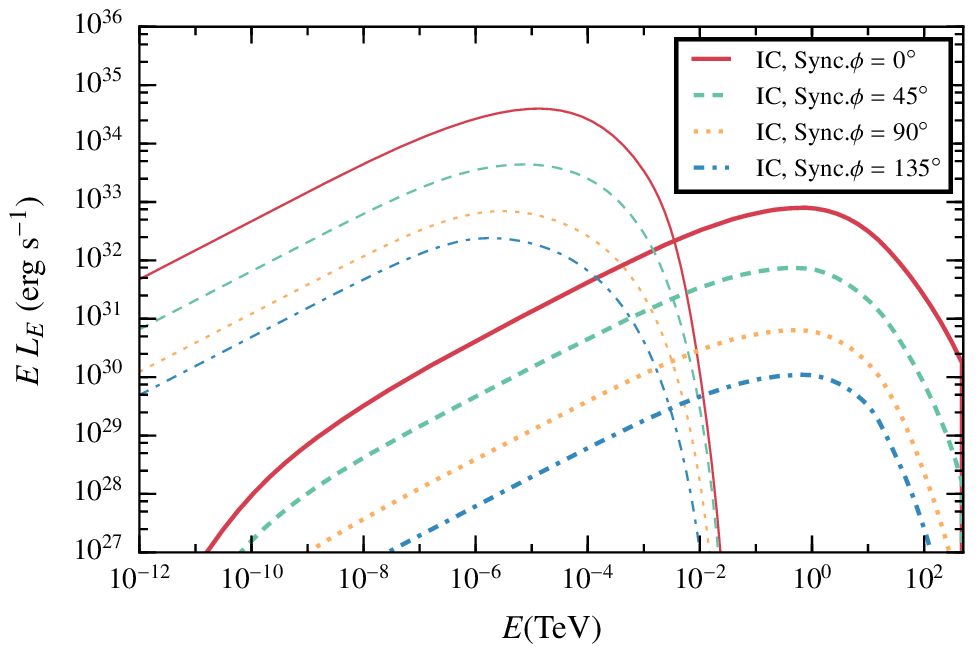
Results. high magnetic field, steady state.

In this case the synchrotron emission dominates the spectrum, whereas the IC is very similar.

\chi_B = 0.1
χB=0.1\chi_B = 0.1

Synchrotron emission can play an important role at GeV energies even with not-so-extreme magnetic fields.

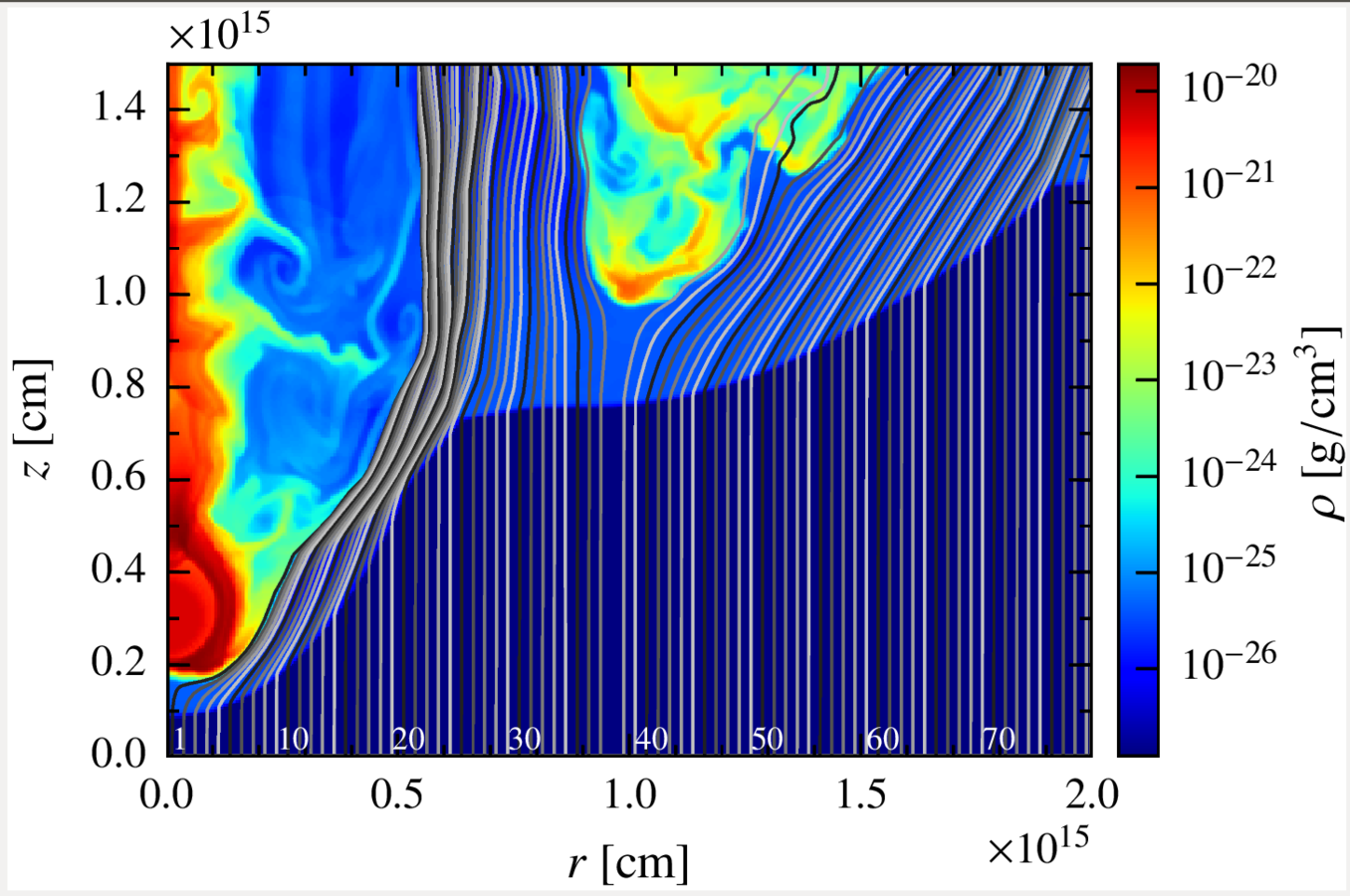
Results. perturbed state.

In some cases, the instabilities can eventually lead to a perturbed state of the shock, increasing the effective area of the emitter.

Results. perturbed state with with different B fields and angles

When the instabilities lead to a perturbed state of the shock, a transient increment of the synchrotron luminosity is expected.

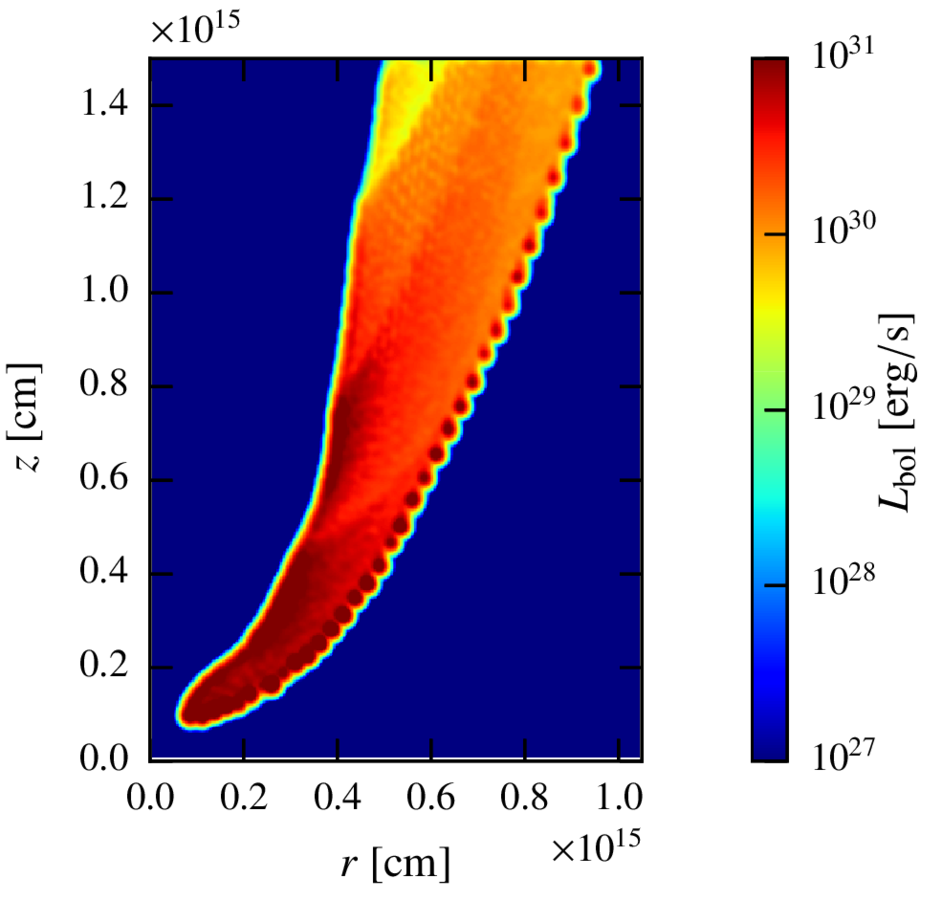
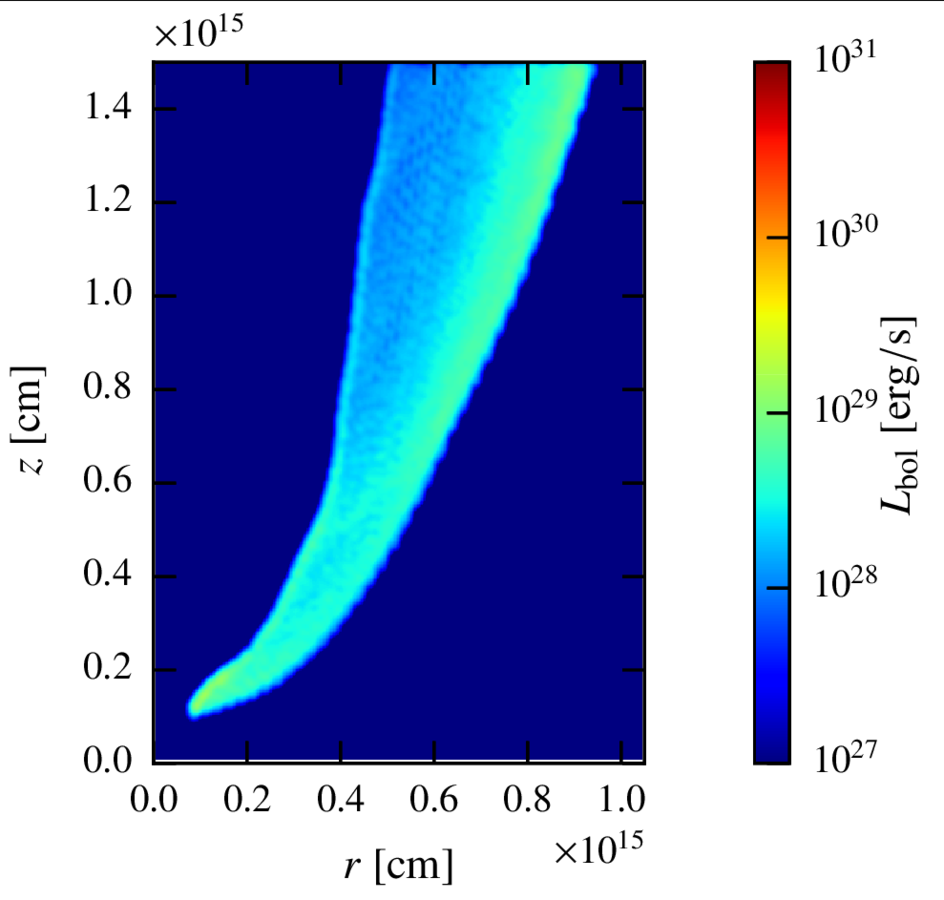
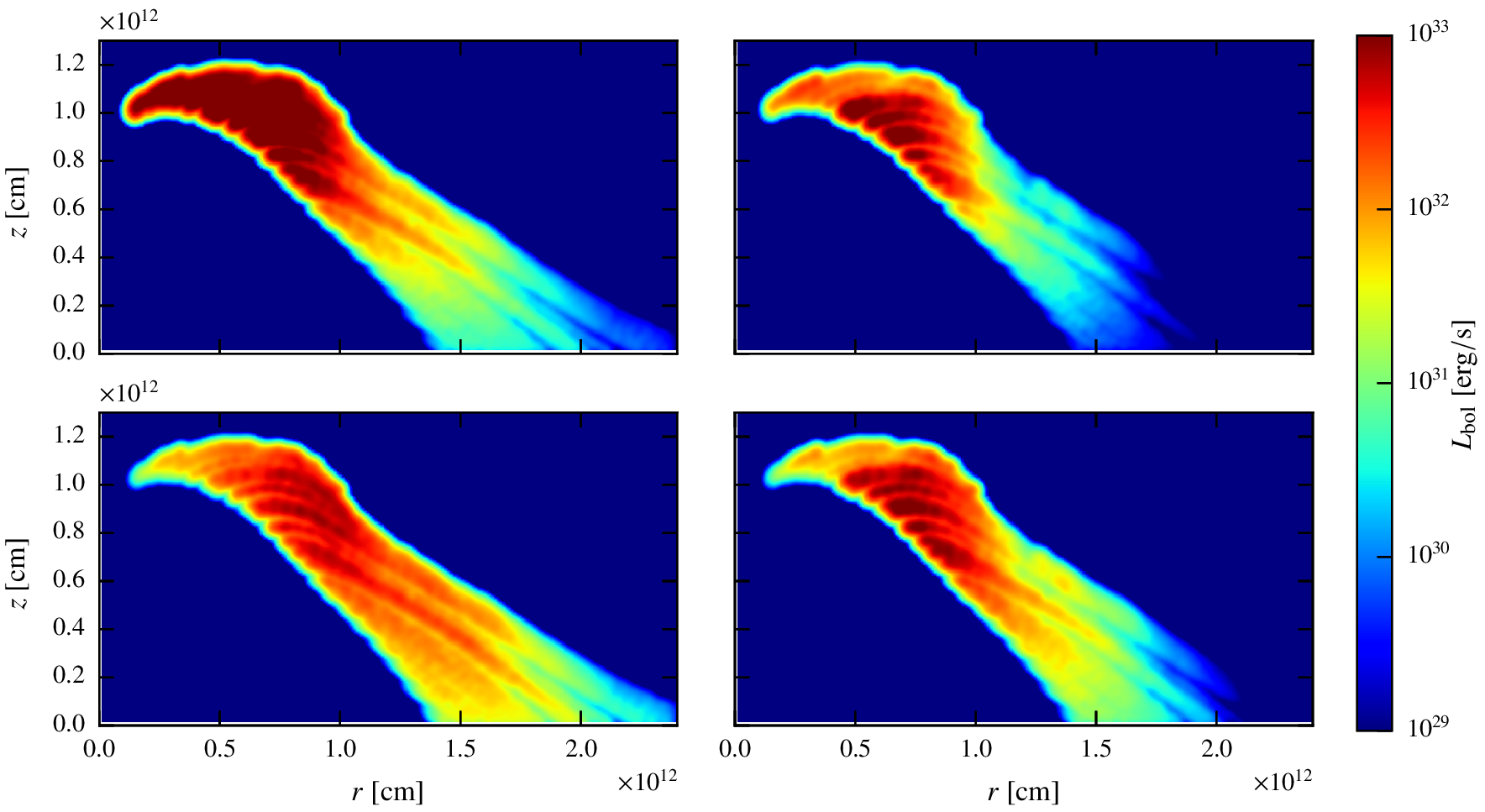
Maps. Steady state.

Inverse compton

The total observer luminosity in this case is:

r < r_{CD}
r<rCDr < r_{CD}
\chi_B = 10^{-4},\,\,\phi = 0^\circ
χB=10−4,ϕ=0∘\chi_B = 10^{-4},\,\,\phi = 0^\circ

Whereas the luminosity of the region with

L_{IC}=5 \times 10^{34} \text{erg s}^{-1}
LIC=5×1034erg s−1L_{IC}=5 \times 10^{34} \text{erg s}^{-1}

is ~100 times smaller, so the effective size of the emitter is much larger than the CD region.

Maps. Steady state.

synchrotron

The total observer luminosity in this case is:

For the synchrotron, the emission is even more equally distributed through the shock, because it does not depend on the external photon field.

L_{sync}=2.5 \times 10^{32} \text{erg s}^{-1}
Lsync=2.5×1032erg s−1L_{sync}=2.5 \times 10^{32} \text{erg s}^{-1}
\chi_B = 10^{-4},\,\,\phi = 0^\circ
χB=10−4,ϕ=0∘\chi_B = 10^{-4},\,\,\phi = 0^\circ

Maps. perturbed state.

Inverse compton

synchrotron

\chi_B = 10^{-4},\,\,\phi = 0^\circ
χB=10−4,ϕ=0∘\chi_B = 10^{-4},\,\,\phi = 0^\circ

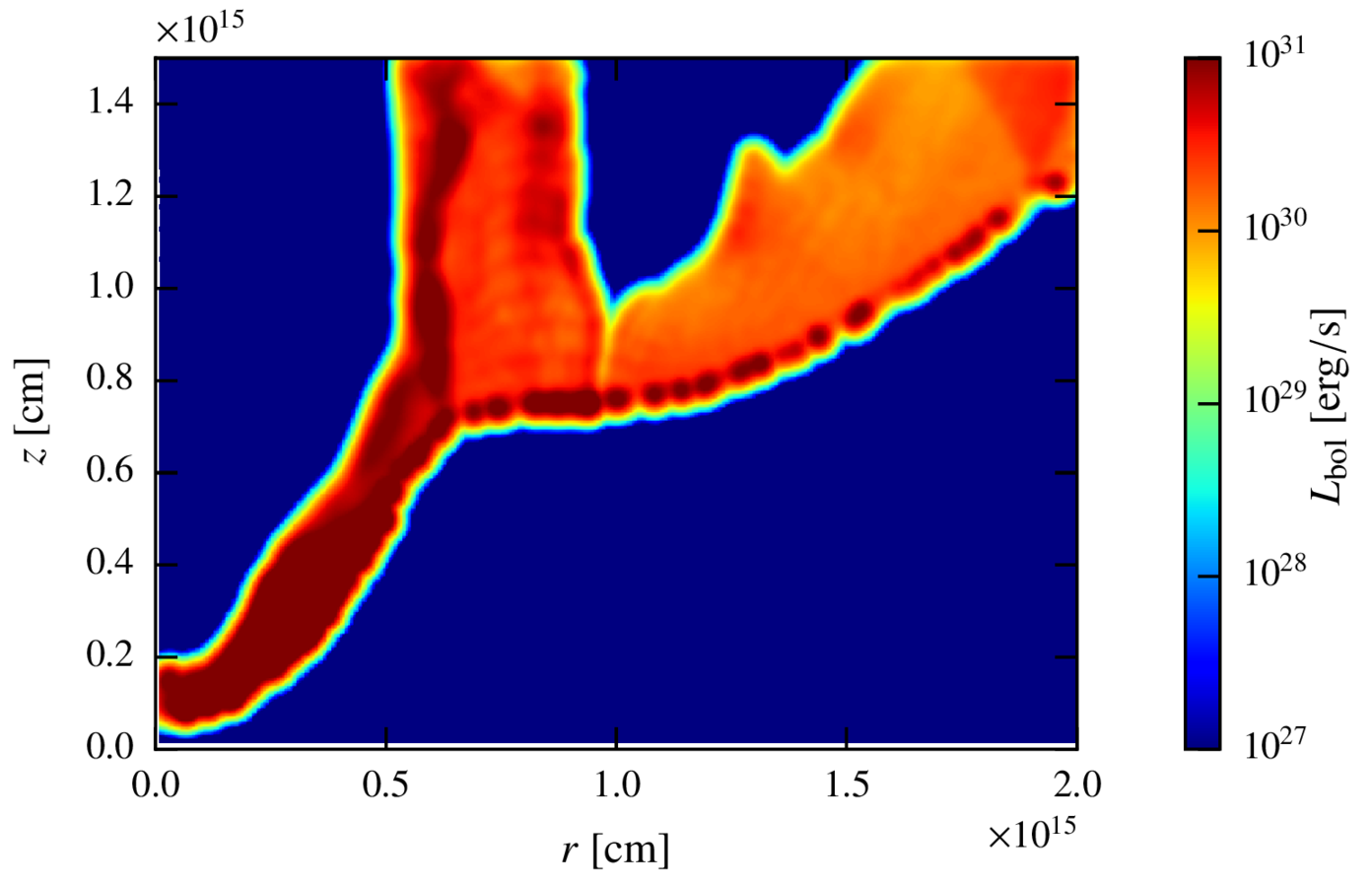
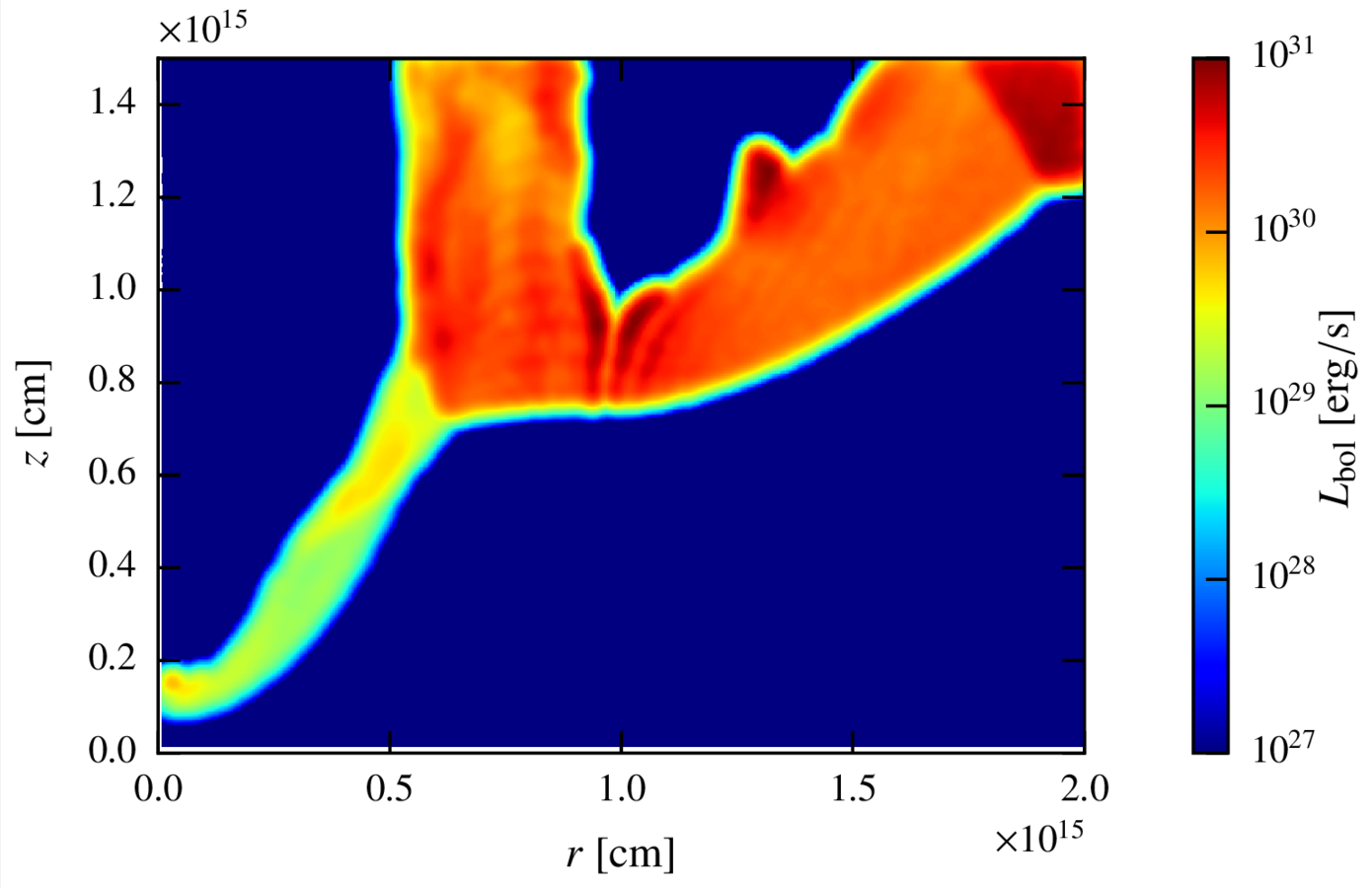
Discussion. Scalability of the results

\chi_B = 10^{-4},\,\,\theta = 0^\circ
χB=10−4,θ=0∘\chi_B = 10^{-4},\,\,\theta = 0^\circ

Our hydrodinamical simulation places the star at a jet height of z = 10pc, but the results can be easily scaled with z.

L_\text{rad}\propto 1/z
Lrad∝1/zL_\text{rad}\propto 1/z

If the losses are dominated by escape:

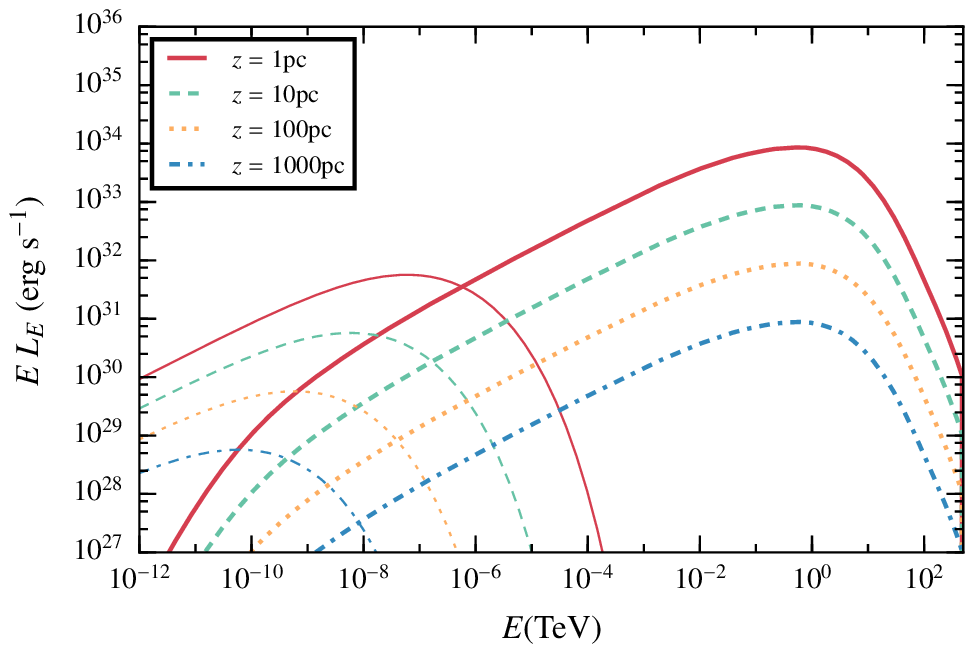
AGN jet - star interactions. Conclusions.

  • The effective radius of the emitter is much bigger than the contact discotinuity radius. 
  • Emission levels strongly depend on the viewer angle due to Doppler boosting.
  • The non-thermal luminosity for a single star points towards potentially detectable luminosities for typical populations crossing AGN jets, according to Bosch-Ramón 15 estimates.

V. M. de la Cita, V. Bosch-Ramon, X. Paredes-Fortuny, D. Khangulyan and M. Perucho, 2016, A&A, 591, A15

Outline of the talk

  • gamma-ray sources with relativistic outflows

  • Methods: coupling hydrodynamics and NT calculation

  • star-jet interactions in active galactic nuclei

  • pulsar wind interacting with a clumpy stellar wind

  • clumpy wind-jet interacions in high-mass microquasars

We consider a binary system consisting on a massive star (O type) and a pulsar with a relativistic wind.

Massive stars present strong inhomogeneities in their winds, or clumps (Owocki & Cohen 2006, Moffat 2008). This clumps can introduce inertia in the system, forming shocks inside the jet. 

Gamma-ray binaries: Early-type star + pulsar 

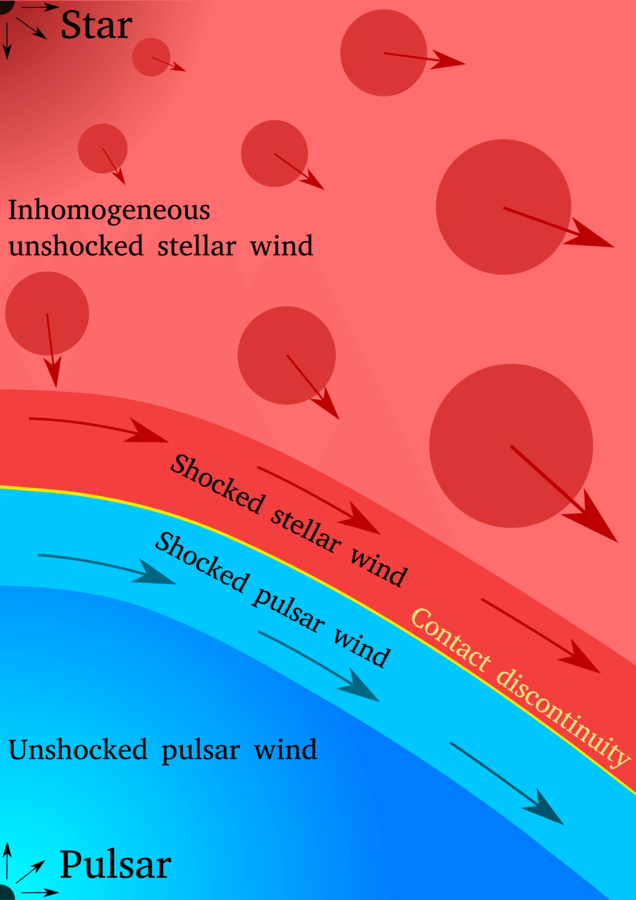
​Paredes-Fortuny et al. 2015

Going into details. hidrodynamic setup.

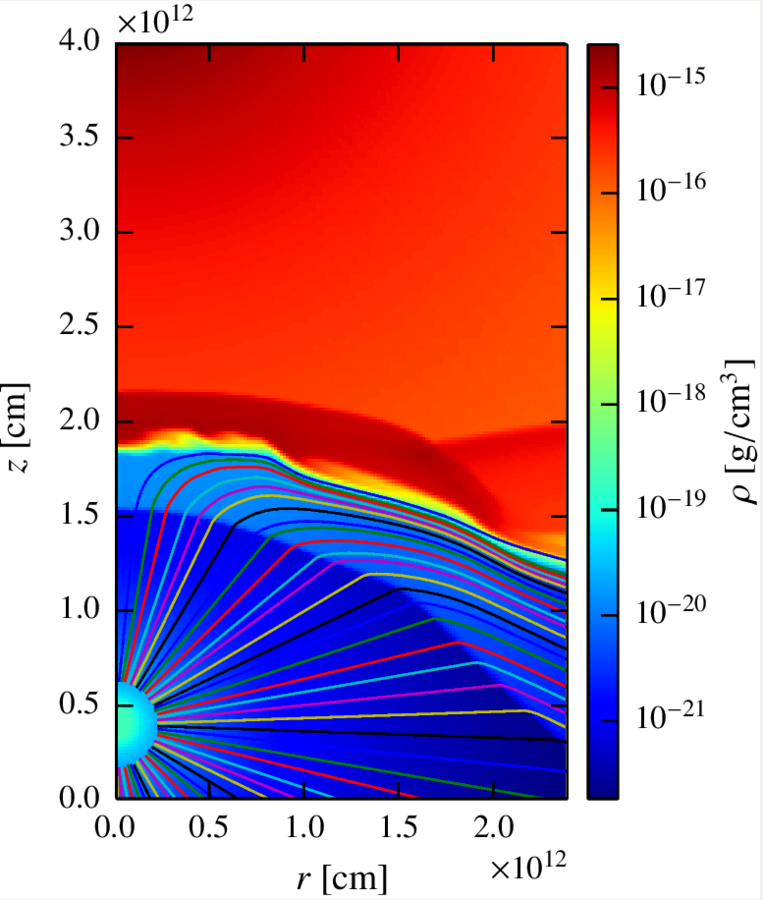
We consider a single clump-wind interaction, with the clump placed between the pulsar and the star. 

To do so, we first impose an homogeneous wind until we reach a stationary state and then we add a clump of a given size and density.

T_{\star} = 4\times 10^4 \text{ K}
T⋆=4×104 KT_{\star} = 4\times 10^4 \text{ K}
L_{\star} = 10^{39} \text{erg s}^{-1}
L⋆=1039erg s−1L_{\star} = 10^{39} \text{erg s}^{-1}
\vec{v}_{wind,\star} = 3000 \text{ km s}^{-1}
v⃗wind,⋆=3000 km s−1\vec{v}_{wind,\star} = 3000 \text{ km s}^{-1}
\dot{M}_\star = 10^{-7} M_\odot \text{yr}^{-1}
M˙⋆=10−7M⊙yr−1\dot{M}_\star = 10^{-7} M_\odot \text{yr}^{-1}
R_c = 1 \text{ or }5 \text{ in units of } a, \text{ with }\,\, a = 8\times 10^{10} \text{ cm}
Rc=1 or 5 in units of a, with a=8×1010 cmR_c = 1 \text{ or }5 \text{ in units of } a, \text{ with }\,\, a = 8\times 10^{10} \text{ cm}

Clump radius:

Our workframe

The pulsar has a spin-down luminosity of:

And a wind Lorentz factor of:

L_{sd} = 10^{37}\text{ erg s}^{-1}
Lsd=1037 erg s−1L_{sd} = 10^{37}\text{ erg s}^{-1}
\Gamma = 5
Γ=5\Gamma = 5
z_\star = 4.4\times 10^{12} \text{ cm}
z⋆=4.4×1012 cmz_\star = 4.4\times 10^{12} \text{ cm}
z_p = 4\times 10^{11} \text{ cm}
zp=4×1011 cmz_p = 4\times 10^{11} \text{ cm}

Going into details. Structure of the shock. 

​Paredes-Fortuny et al. 2015

Going into details. Physical assumptions.

Magnetic field perpendicular to the fluid line

\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0cv)
B0′24π=χB(ρ0h0cv)\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0cv)
\chi_B = 10^{-3}, 0.1
χB=10−3,0.1\chi_B = 10^{-3}, 0.1

Definition of the magnetic field at the beginning of the line:

(Low, high magnetic field)

Fraction of matter energy flux that goes to magnetic energy (Poynting flux)

Photon field:

T_{\star} = 4\times 10^4 \text{ K}
T⋆=4×104 KT_{\star} = 4\times 10^4 \text{ K}
L_{\star} = 10^{39} \text{erg s}^{-1}
L⋆=1039erg s−1L_{\star} = 10^{39} \text{erg s}^{-1}

injection of non-thermal particles in the fluid:

A fraction of the generated internal energy per second in a given cell (at the shocks) is transferred to non-thermal particles.

\chi = 0.1
χ=0.1\chi = 0.1

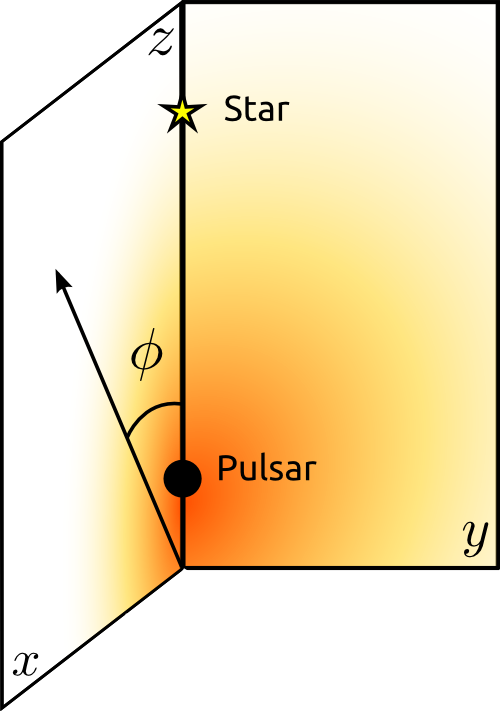
Going into details. observer angle.

The observer is placed in the z-r plane, forming an angle phi with the z axis.

To avoid eclipses, we do not simulate the extreme angles 0º and 180º. Instead, three intermediate angles are studied:

45º, 90º and 135º.

Low B

High B

\chi_B = 10^{-3}
χB=10−3\chi_B = 10^{-3}
\chi_B = 0.1
χB=0.1\chi_B = 0.1

Results. two magnetic fields.

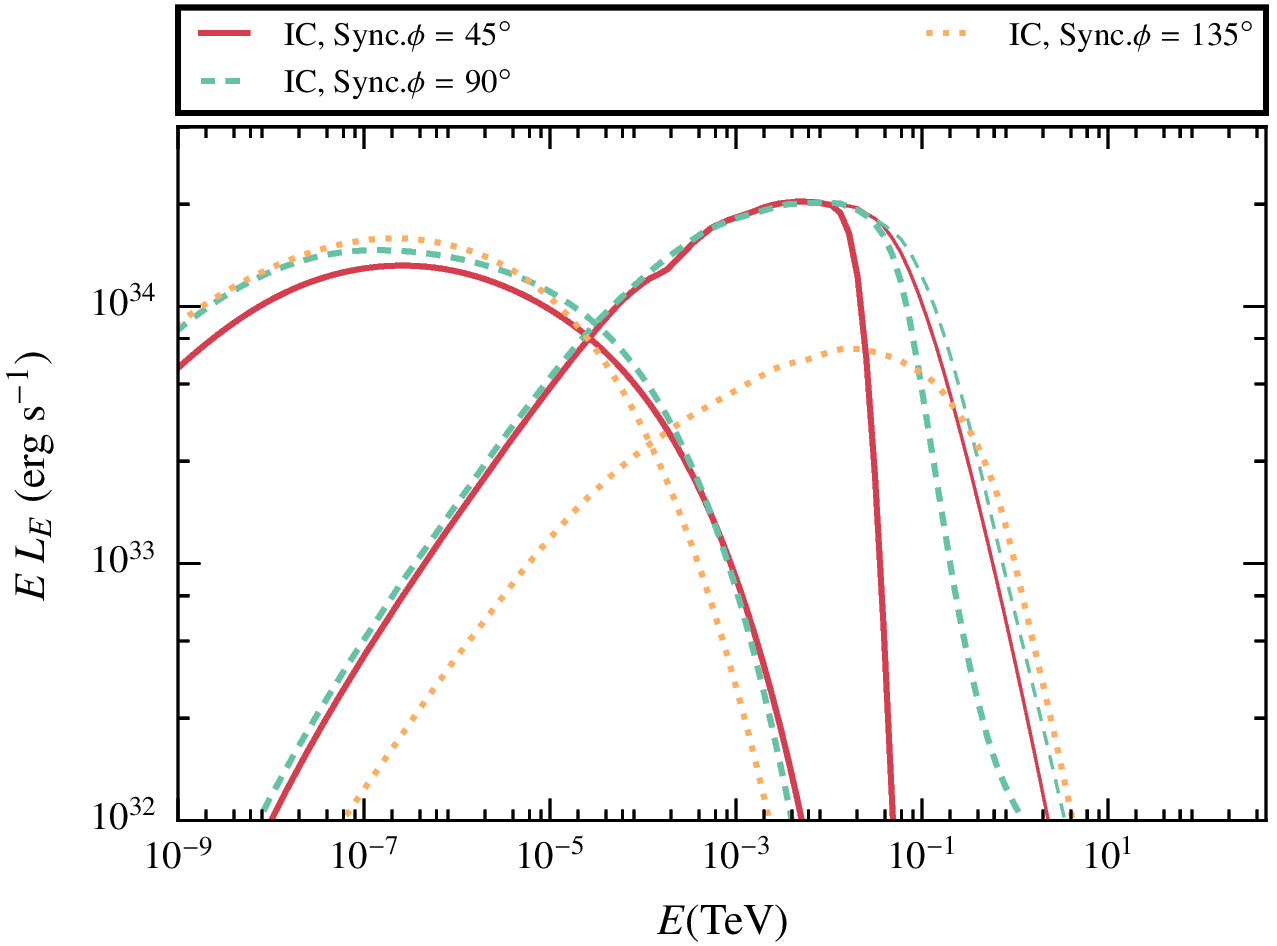
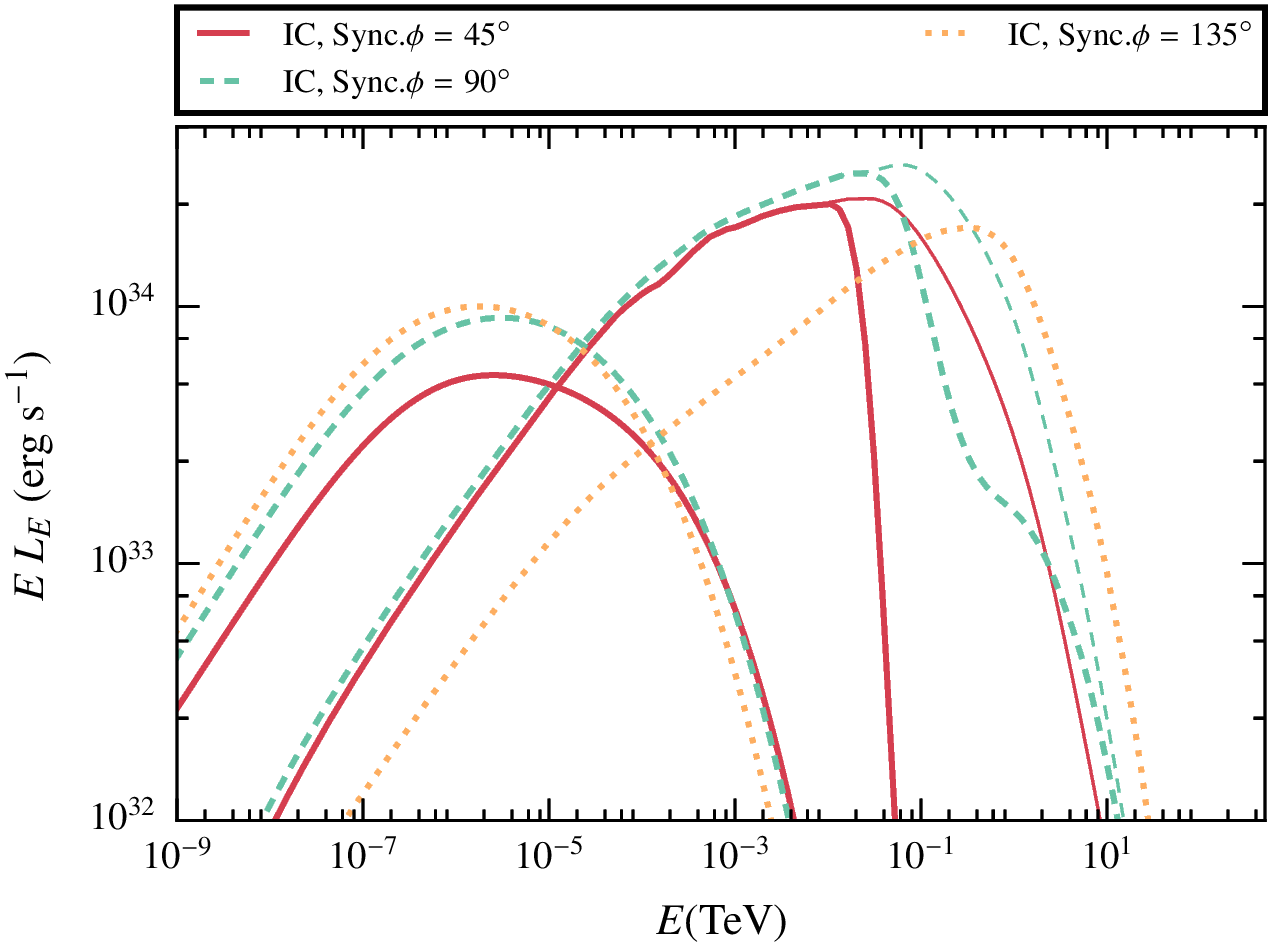
Results. Extended vs point-like emitter.

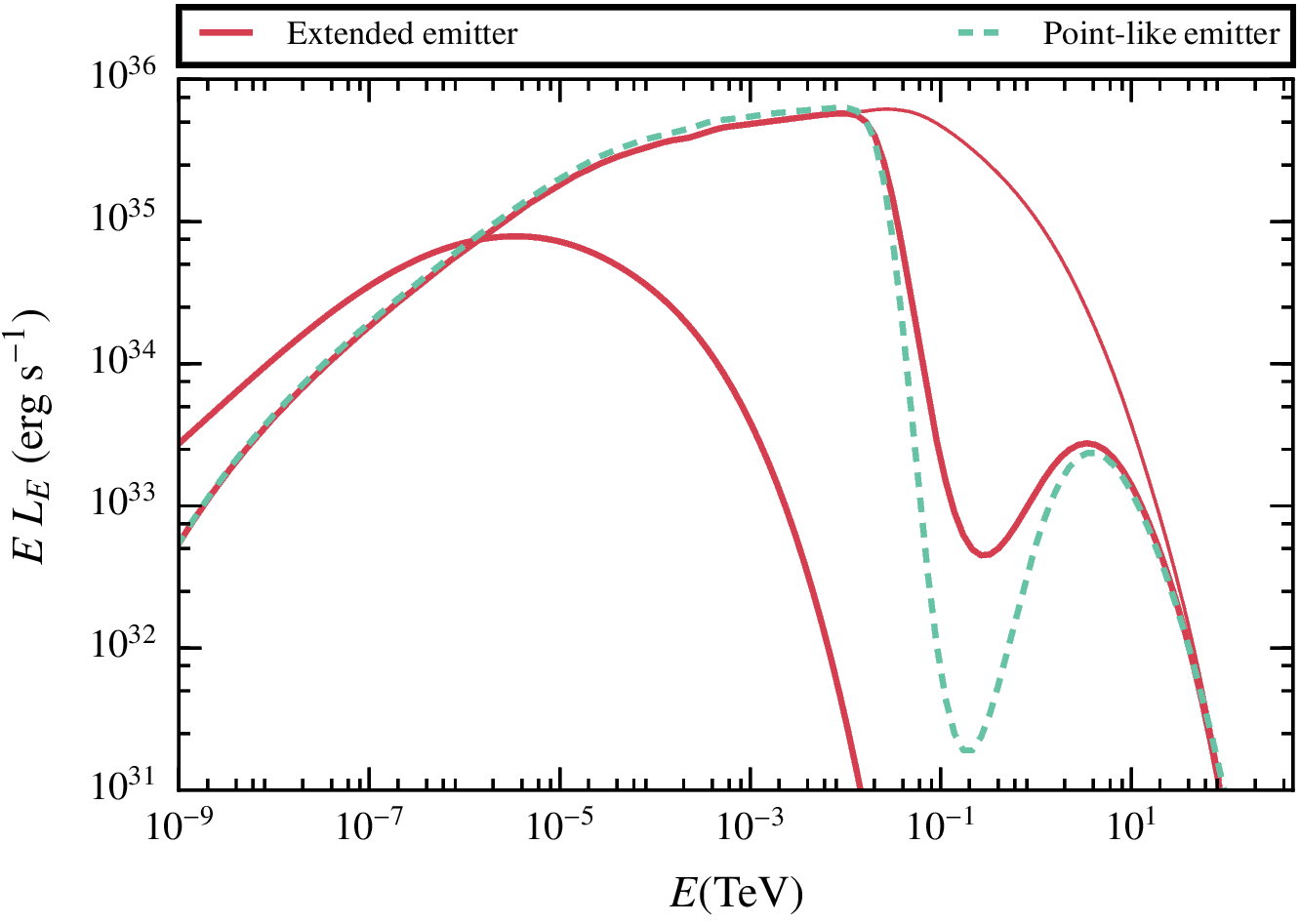
The importance of the hydrodynamic study of the problem is clear when we compare the results obtained assuming a point-like emitter.

A proper characterisation of the emitter is key for the understanding of the SED.

Results. MAPS OF THE no-CLUMP SCENARIO.

\text{IC, }\phi = 45^\circ
IC, ϕ=45∘\text{IC, }\phi = 45^\circ
\text{IC, }\phi = 135^\circ
IC, ϕ=135∘\text{IC, }\phi = 135^\circ
\text{Sync, }\phi = 45^\circ
Sync, ϕ=45∘\text{Sync, }\phi = 45^\circ
\text{Sync, }\phi = 135^\circ
Sync, ϕ=135∘\text{Sync, }\phi = 135^\circ

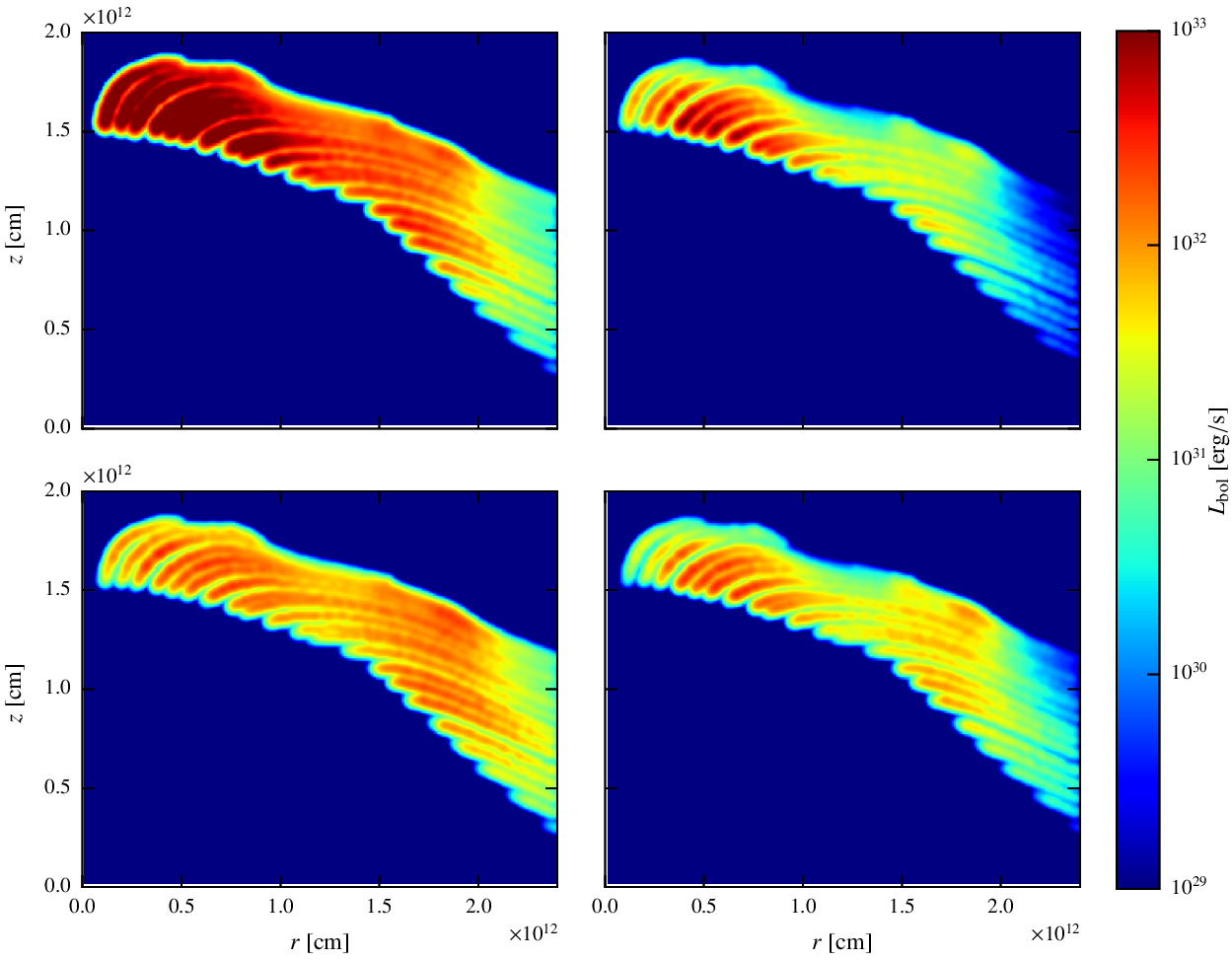
Results. Maps of the big clump scenario.

\text{IC, }\phi = 45^\circ
IC, ϕ=45∘\text{IC, }\phi = 45^\circ
\text{IC, }\phi = 135^\circ
IC, ϕ=135∘\text{IC, }\phi = 135^\circ
\text{Sync, }\phi = 45^\circ
Sync, ϕ=45∘\text{Sync, }\phi = 45^\circ
\text{Sync, }\phi = 135^\circ
Sync, ϕ=135∘\text{Sync, }\phi = 135^\circ

pulsar wind + clump. conclusions.

V. M. de la Cita, V. Bosch-Ramon, X. Paredes-Fortuny, D. Khangulyan  and M. Perucho A&A 598, A13 (2017)

  • The Doppler boosting effect is very important in the understanding of these systems.
  • Strong instabilities take place easily, and together with the Doppler effect a variable short-time output is expected.
  • The main effect of the clump is to move the shocked region closer to the pulsar, which affects the radiation normalisation and SED shape.

Outline of the talk

  • gamma-ray sources with relativistic outflows

  • Methods: coupling hydrodynamics and NT calculation

  • star-jet interactions in active galactic nuclei

  • pulsar wind interacting with a clumpy stellar wind

  • clumpy wind-jet interacions in high-mass microquasars

high-mass Microquasars (HMMQ)

  • Microquasar jets:  the donor star transfers matter to the compact object, forming an accretion disk around it and two relativistic jets.
  • High-mass microquasar: the winds of the massive donor star (O, B type) are expected to be strongly inhomogeneous, presenting overdensities (clumps) that may interact with the jet.
Owocki & Cohen '06, Moffat '08

gamma ray emission. cygnus x-1 and cygnus x-3

Cygnus X-1

Cygnus X-3

AGILE Collaboration

Both detected in GeV by Fermi satellite, when  the jet is present

physical scenario 

​​Credit: F. Mirabel
  • Proposed by Owocki et al. 09, first analytical estimates by Araudo et al. '09 and detailed three-dimensional simulations by  Perucho et al. '12 
  • Here we couple for the first time relativistic hydrodynamical (RHD) simulations with non-thermal radiative calculations.
  • Along with a semi-analytical description of the frequency and characteristics of this jet-clumps interactions.

first considerations. jet penetrability.

R_{cl} > 3\times10^{10} \left(\frac{\theta_{j}}{0.1}\right) \left(\frac{10}{\chi}\right) \left(\frac{R_{orb}}{3\times10^{12}\mathrm{cm}}\right) \mathrm{cm}
Rcl>3×1010(θj0.1)(10χ)(Rorb3×1012cm)cmR_{cl} > 3\times10^{10} \left(\frac{\theta_{j}}{0.1}\right) \left(\frac{10}{\chi}\right) \left(\frac{R_{orb}}{3\times10^{12}\mathrm{cm}}\right) \mathrm{cm}

The minimum radius for a clump to enter the jet is:

The maximum jet luminosity not to destroy the jet before it enters:

L_j < 1.4\times 10^{37} \, \big(\frac{\Gamma_j-1}{\Gamma_j}\big) \big(\frac{\chi}{10}\big) \big(\frac{\dot{M}_w}{3\times 10^{-6} M_\odot \text{yr}^{-1}}\big)
Lj<1.4×1037(Γj−1Γj)(χ10)(M˙w3×10−6M⊙yr−1)L_j < 1.4\times 10^{37} \, \big(\frac{\Gamma_j-1}{\Gamma_j}\big) \big(\frac{\chi}{10}\big) \big(\frac{\dot{M}_w}{3\times 10^{-6} M_\odot \text{yr}^{-1}}\big)
\big(\frac{\theta_j}{0.1}\big)^2 \big(\frac{v_w}{10^8 \text{cm s}^{-1}}\big)\big(\frac{v_j}{c}\big)^{-1} \text{erg} \, \text{s}^{-1}
(θj0.1)2(vw108cm s−1)(vjc)−1ergs−1\big(\frac{\theta_j}{0.1}\big)^2 \big(\frac{v_w}{10^8 \text{cm s}^{-1}}\big)\big(\frac{v_j}{c}\big)^{-1} \text{erg} \, \text{s}^{-1}

jet opening angle

contrast density

orbital radius

R_{cl}
RclR_{cl}
L_{j}
LjL_{j}

stellar wind speed

jet Lorentz factor

stellar mass-loss rate

\theta_{j}
θj\theta_{j}
\frown
⌢\frown
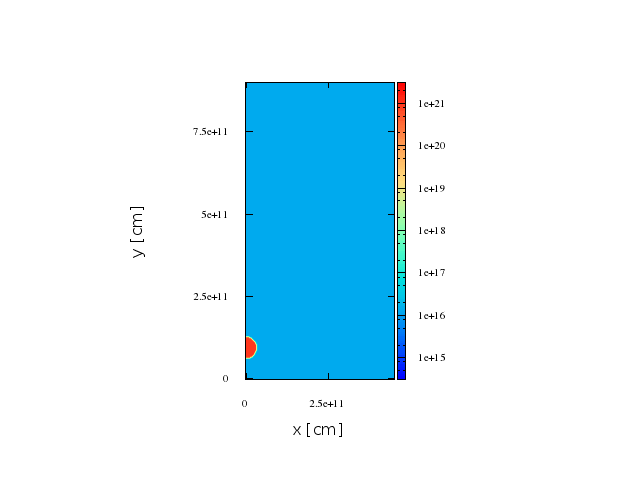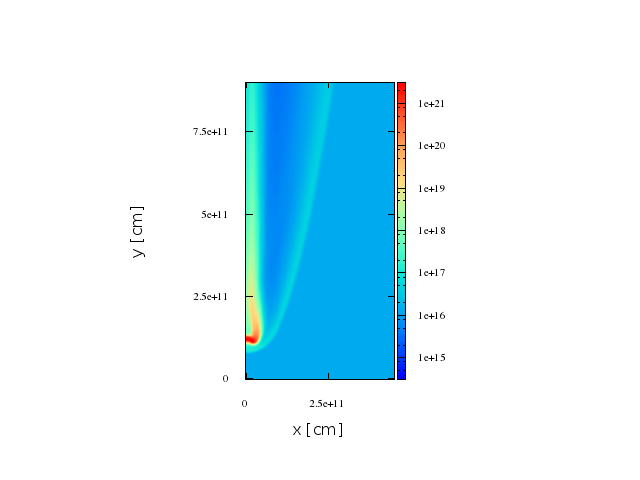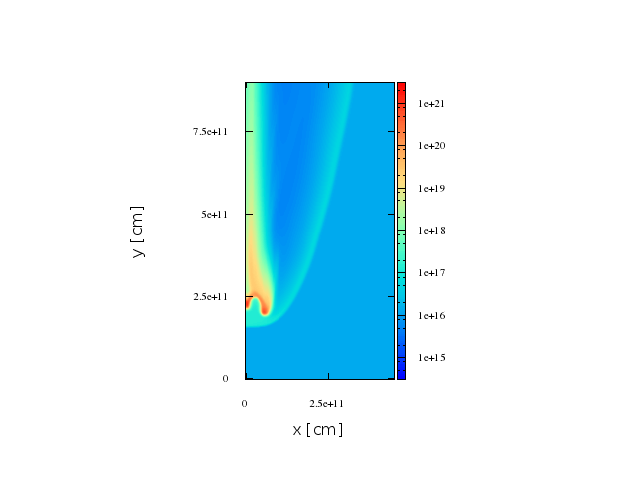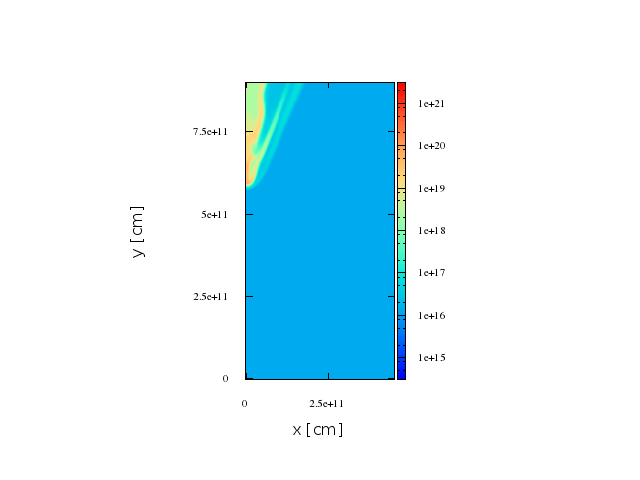
Jet
direction
L_\text{jet} \sim 10^{37}\text{ erg s}^{-1}
Ljet∼1037 erg s−1L_\text{jet} \sim 10^{37}\text{ erg s}^{-1}
\Gamma = 2
Γ=2\Gamma = 2
\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
v⃗stellar wind=2000 km s−1\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
\dot{M}_\star = 3 \times 10^{-6} M_\odot \text{yr}^{-1}
M˙⋆=3×10−6M⊙yr−1\dot{M}_\star = 3 \times 10^{-6} M_\odot \text{yr}^{-1}

O-type Star

x_\star = (-3,-3)\times 10^{12} \mathrm{cm}
x⋆=(−3,−3)×1012cmx_\star = (-3,-3)\times 10^{12} \mathrm{cm}
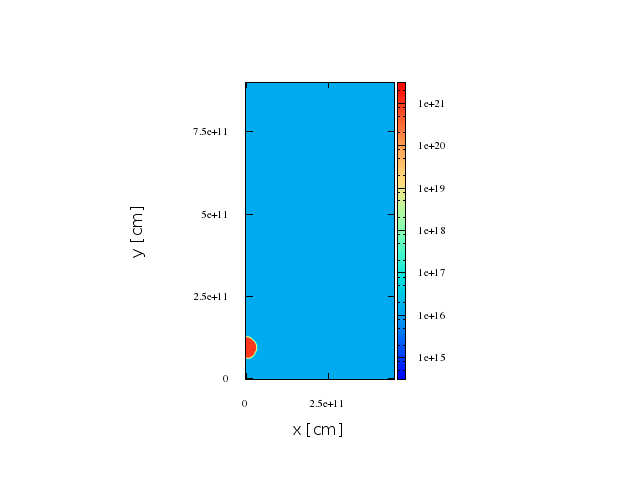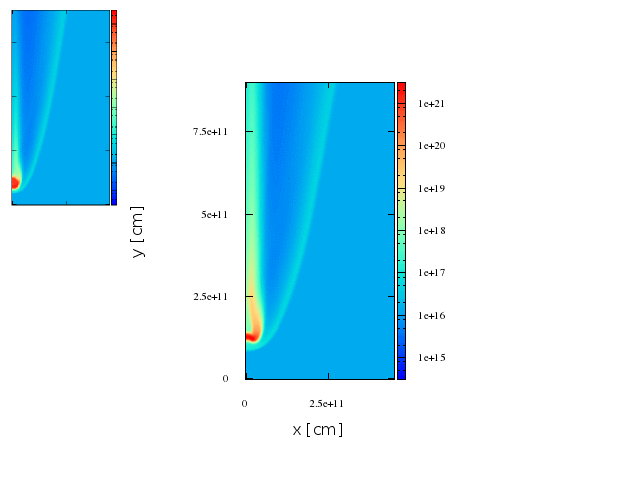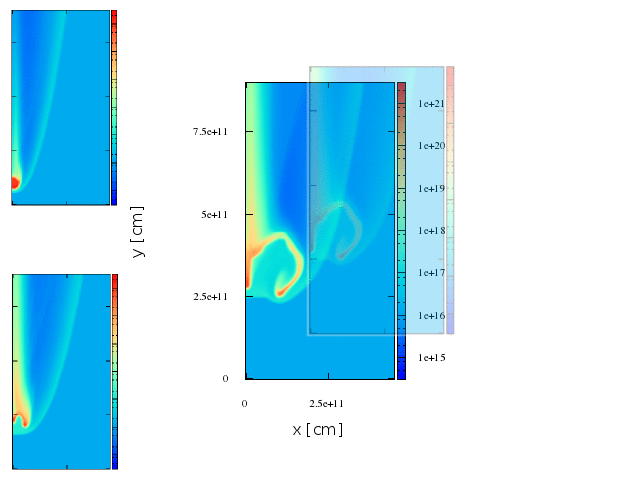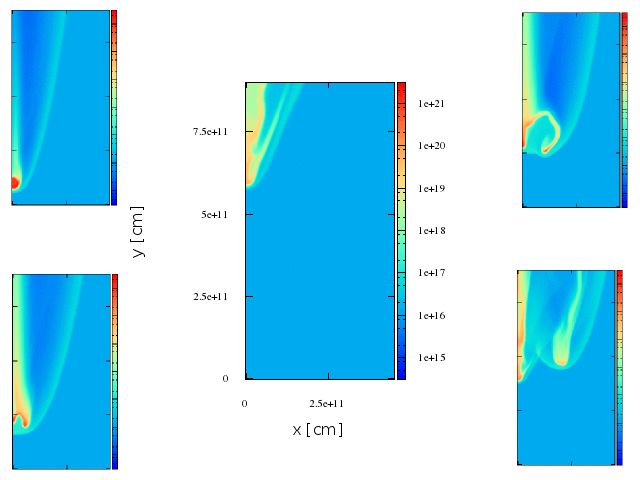
~8.5 min
~1 min
~12 min
~10 min
~14 min
First stage
Second stage

Going into details. hydrodynamic setup.

The fluid is divided in 50 lines with 200 cells each, describing an axisymmetric 2D space of:

r\in[0,4.5]\times10^{11}\text{ cm}
r∈[0,4.5]×1011 cmr\in[0,4.5]\times10^{11}\text{ cm}
y\in[0,9]\times10^{11}\text{ cm}
y∈[0,9]×1011 cmy\in[0,9]\times10^{11}\text{ cm}

The clump radius, height and density contrast are:

r_{cl}=3\times10^{10}\text{ cm}
rcl=3×1010 cmr_{cl}=3\times10^{10}\text{ cm}
z_{cl}=3\times10^{12}\text{ cm}
zcl=3×1012 cmz_{cl}=3\times10^{12}\text{ cm}
\chi=10
χ=10\chi=10

Half the solar radius

A fifth of an Astronomical Unit

Going into details. Physical assumptions.

Magnetic field perpendicular to the fluid line

\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0c^2)
B0′24π=χB(ρ0h0c2)\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0c^2)
B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
Bk′=B0′(ρkv0Γ0ρ0vkΓk)1/2B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
\chi_B = 10^{-4}, 1
χB=10−4,1\chi_B = 10^{-4}, 1

Definition of the magnetic field at the beginning of the line:

Evolution of the B field in the different cells k:

(Low, high magnetic field)

Fraction of matter energy flux that goes to magnetic energy

Photon field:

T_{\star} = 4\times 10^4 \text{ K}
T⋆=4×104 KT_{\star} = 4\times 10^4 \text{ K}
L_{\star} = 1\times 10^{39} \text{erg s}^{-1}
L⋆=1×1039erg s−1L_{\star} = 1\times 10^{39} \text{erg s}^{-1}

injection of non-thermal particles

A fraction of the generated internal energy per second in the cell k enters in the form of non-thermal particles.

\chi = 0.1
χ=0.1\chi = 0.1

Biggest uncertainty

Going into details. Observer angle.

To get a feeling of the importance of the observer angle, we have chosen the following angles:

  • 0º - with the jet pointing at the observer
  • 30º - representative of Cygnus X-1
  • 90º - the observer is placed in the x axis

The observer will be placed in the x axis forming an angle phi with the vertical axis. 

\phi = 0^\circ, 30^\circ, 90^\circ
ϕ=0∘,30∘,90∘\phi = 0^\circ, 30^\circ, 90^\circ

Results. First case, smaller shocked region

In the case of a low magnetic field, the IC radiation dominates the spectrum.

The difference between the three angles come from the doppler boosting, more important for smaller angles given that most of the cells have a strong z- component of the  velocity

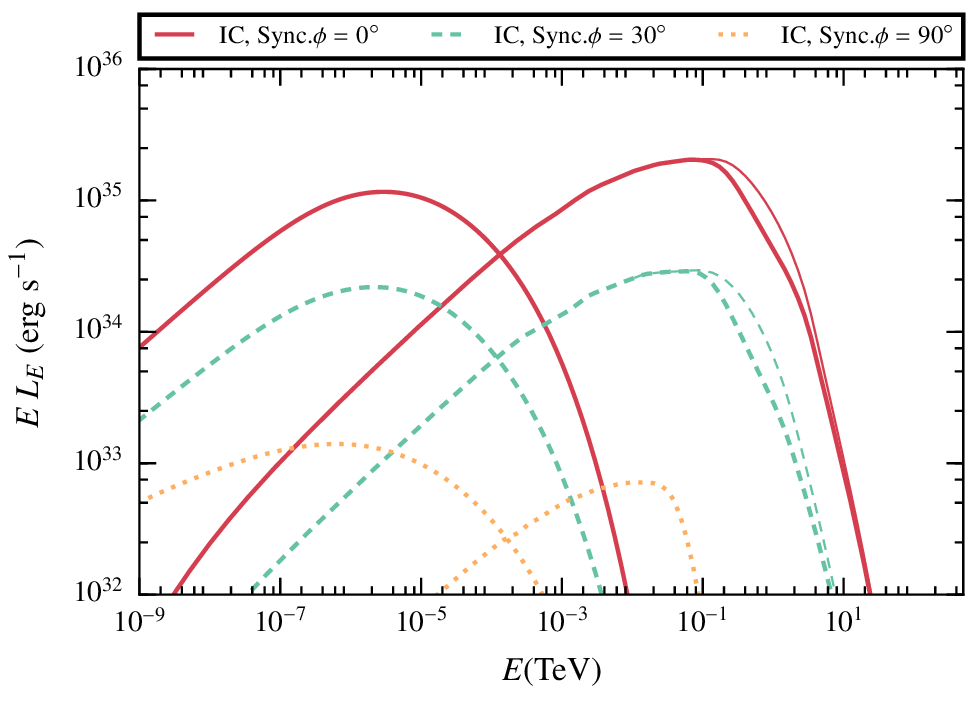
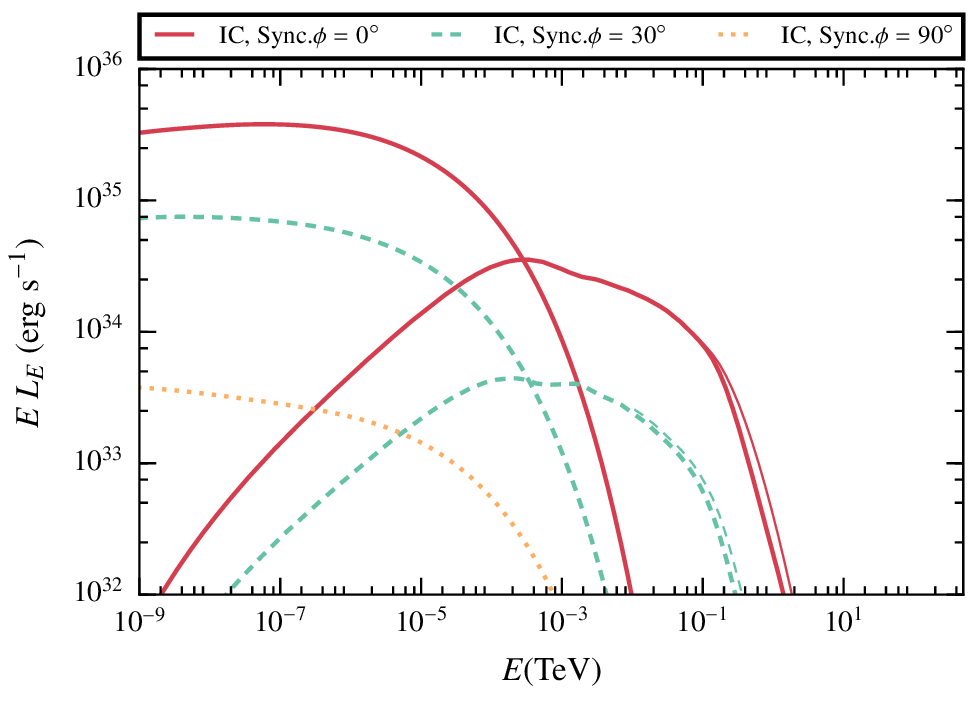
Low B

High B

\chi_B = 10^{-4}
χB=10−4\chi_B = 10^{-4}
\chi_B = 1
χB=1\chi_B = 1
10^{35} \text{ erg s}^{-1}
1035 erg s−110^{35} \text{ erg s}^{-1}

Low B

High B

\chi_B = 10^{-4}, \phi = 30^\circ
χB=10−4,ϕ=30∘\chi_B = 10^{-4}, \phi = 30^\circ
\chi_B = 1, \phi = 30^\circ
χB=1,ϕ=30∘\chi_B = 1, \phi = 30^\circ

Results. comparison between the two cases.

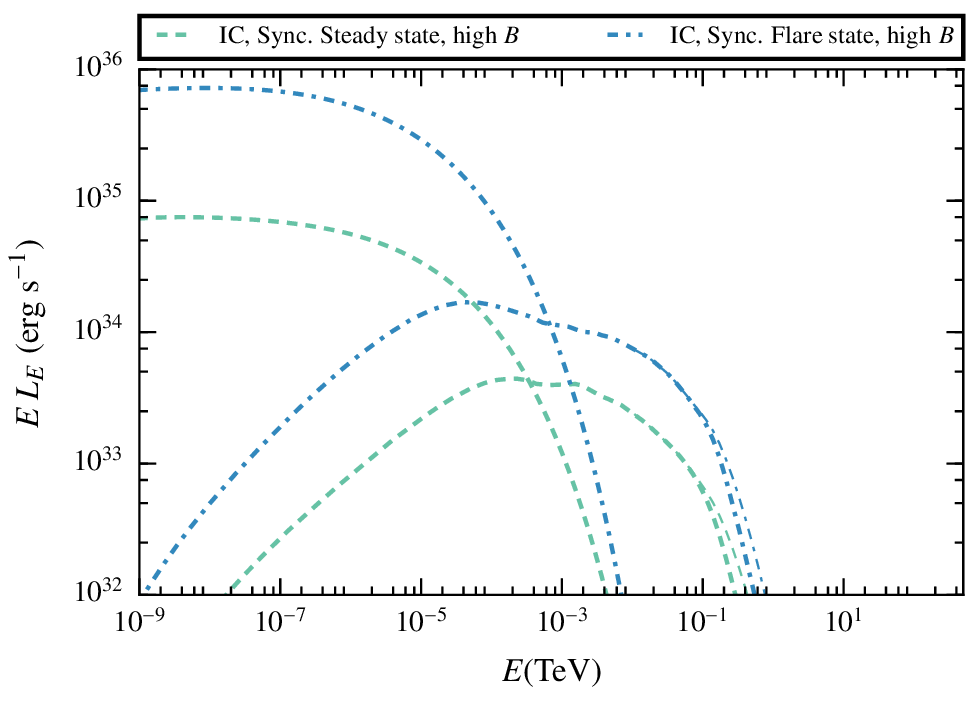
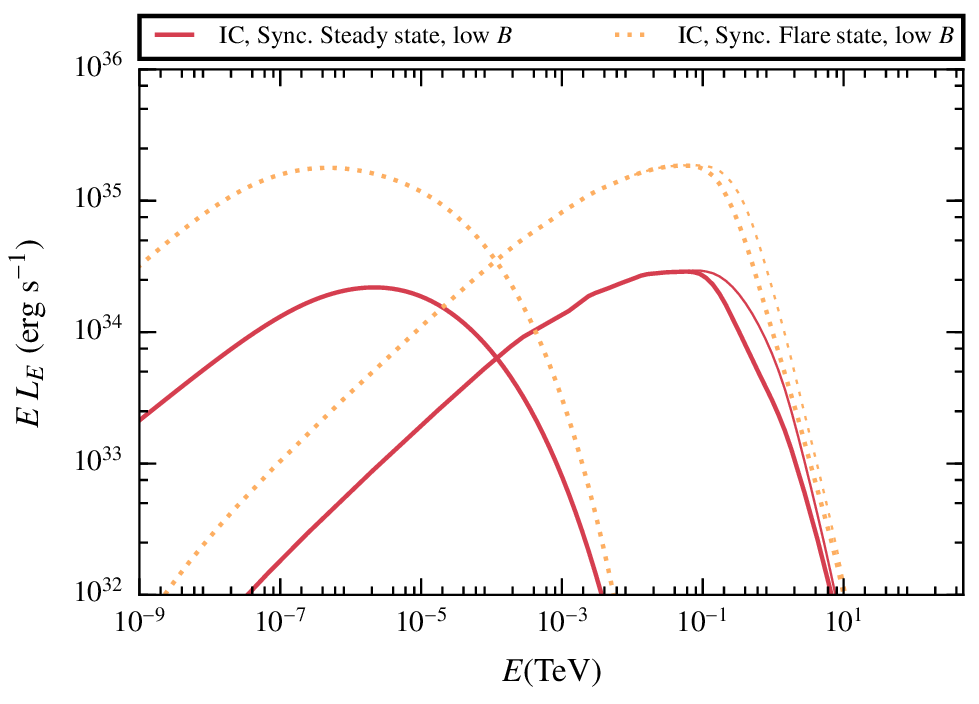
In general the non-thermal radiation will be increased for larger shocks, produced while the clumps is being disrupted.

Results. Duty cycle and standing luminosity.

L_\text{GeV}\approx 10^{35} \text{ erg s}^{-1}
LGeV≈1035 erg s−1L_\text{GeV}\approx 10^{35} \text{ erg s}^{-1}

Knowing the lifetime of a clump inside the jet and the frequency they enter with (for a given clump size) we can compute the duty cycle (DC): the fraction of the time that a certain type of clumps are interacting with the jet.

For a wide variety of parameters we obtain a duty cycle of 1, meaning there is about one clump interacting with the jet at every time .

Cygnus X-1:

Cygnus X-3:

\chi \sim 0.01
χ∼0.01\chi \sim 0.01
\chi \sim 0.1
χ∼0.1\chi \sim 0.1
DC \sim 1
DC∼1DC \sim 1

Results. Cygnus x-1.

V. M. de la Cita S. del Palacio, V. Bosch-Ramon, X. Paredes-Fortuny, G. E. Romero and D. Khangulyan 2017, accepted for publication in A&A

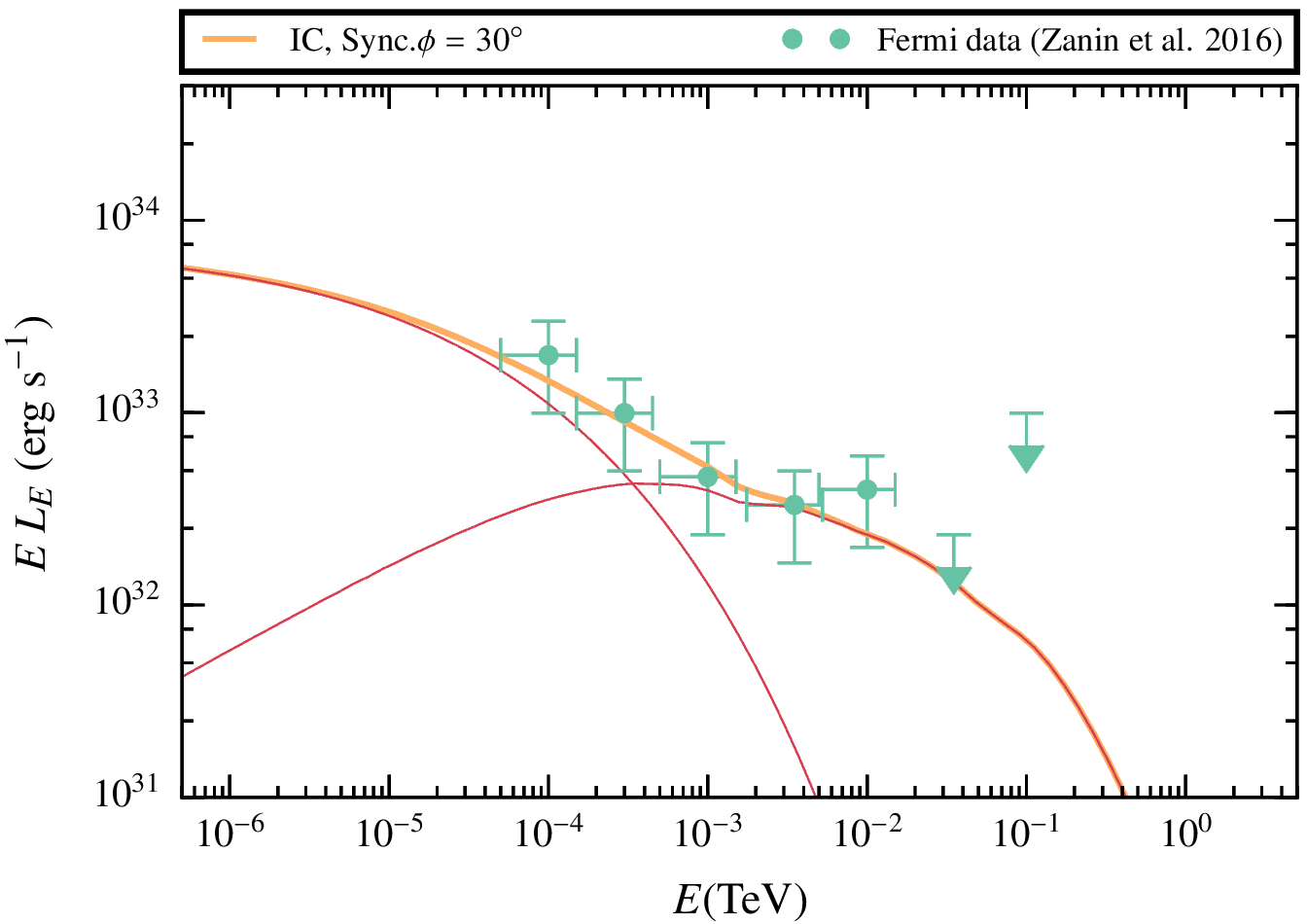
We were able to reproduce the results for Cyg X-1 with a strong magnetic field 

and a relatively conservative NT efficiency

\chi_B = 0.5
χB=0.5\chi_B = 0.5
\chi = 0.01
χ=0.01\chi = 0.01

Thank You.

Backup slide. Injected Luminosity.

The injected non-thermal particles have a lumisosity given by a fraction of the generated internal energy per second in the cell.

L_{inj} = \chi_{NT} \times \dot{U}'_k =
Linj=χNT×U˙k′=L_{inj} = \chi_{NT} \times \dot{U}'_k =

With the pre-factor varying between 0 and 1 and the +/- subindexes refering to the right/left boundaries, respectively.

= \chi_{NT} v_k\Gamma_k^2\times \left(S_+\Gamma_+^2h_+\rho_+c^2\left(1 +\dfrac{v_+^2}{c^2}\right) - S_-\Gamma_-^2h_-\rho_-c^2\left(1 +\dfrac{v_-^2}{c^2}\right)\right)
=χNTvkΓk2×(S+Γ+2h+ρ+c2(1+v+2c2)−S−Γ−2h−ρ−c2(1+v−2c2))= \chi_{NT} v_k\Gamma_k^2\times \left(S_+\Gamma_+^2h_+\rho_+c^2\left(1 +\dfrac{v_+^2}{c^2}\right) - S_-\Gamma_-^2h_-\rho_-c^2\left(1 +\dfrac{v_-^2}{c^2}\right)\right)
Made with Slides.com