Contribution due to clumpy winds to the gamma-ray emission in microquasar jets

s. del palacio, v. bosch-ramon, X. paredes-fortuny, g. e. romero and D. khangulyan

Bilbo, 22th July 2016

V. M. DE LA CITA

high-mass Microquasars (HMMQ)

  • Microquasar jets:  the donor star transfers matter to the compact object, forming an accretion disk around it and two relativistic jets.
  • High-mass microquasar: the winds of the massive donor star (O, B type) are expected to be strongly inhomogeneous, presenting overdensities (clumps) that may interact with the jet.
Owocki & Cohen '06, Moffat '08

gamma ray emission. cygnus x-1 and cygnus x-3

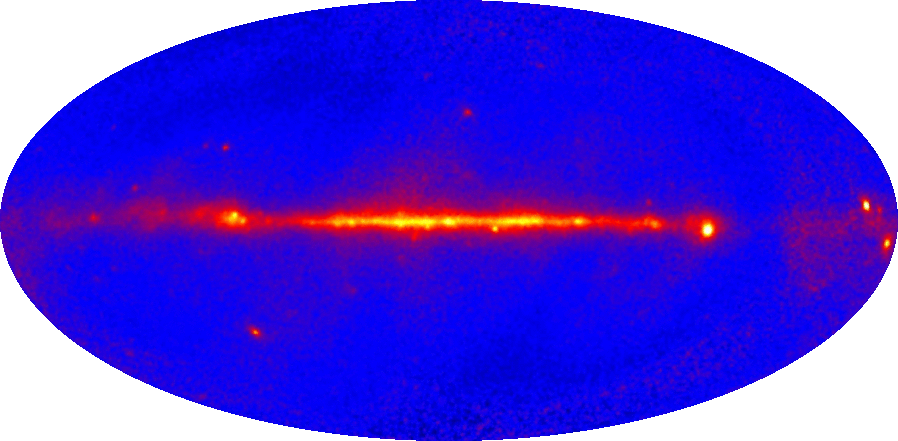
Cygnus X-1

Cygnus X-3

AGILE Collaboration

Both detected in GeV by Fermi satellite, when  the jet is present

physical scenario 

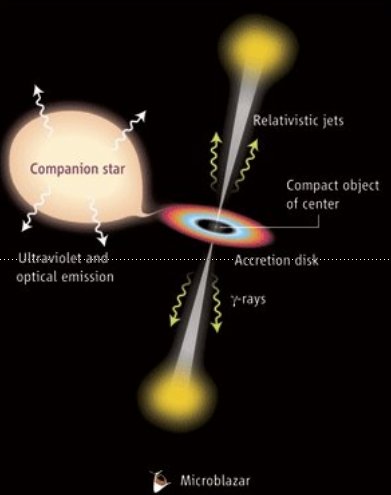
​​Credit: F. Mirabel
  • Proposed by Owocki et al. 09, first analytical estimates by Araudo et al. '09 and detailed three-dimensional simulations by  Perucho et al. '12 
  • Here we couple for the first time relativistic hydrodynamical (RHD) simulations with non-thermal radiative calculations.
  • Along with a semi-analytical description of the frequency and characteristics of this jet-clumps interactions.

first considerations. jet penetrability.

R_{cl} > 3\times10^{10} \left(\frac{\theta_{j}}{0.1}\right) \left(\frac{10}{\chi}\right) \left(\frac{R_{orb}}{3\times10^{12}\mathrm{cm}}\right) \mathrm{cm}
Rcl>3×1010(θj0.1)(10χ)(Rorb3×1012cm)cmR_{cl} > 3\times10^{10} \left(\frac{\theta_{j}}{0.1}\right) \left(\frac{10}{\chi}\right) \left(\frac{R_{orb}}{3\times10^{12}\mathrm{cm}}\right) \mathrm{cm}

The minimum radius for a clump to enter the jet is:

The maximum jet luminosity not to destroy the jet before it enters:

L_j < 1.4\times 10^{37} \, \big(\frac{\Gamma_j-1}{\Gamma_j}\big) \big(\frac{\chi}{10}\big) \big(\frac{\dot{M}_w}{3\times 10^{-6} M_\odot \text{yr}^{-1}}\big)
Lj<1.4×1037(Γj−1Γj)(χ10)(M˙w3×10−6M⊙yr−1)L_j < 1.4\times 10^{37} \, \big(\frac{\Gamma_j-1}{\Gamma_j}\big) \big(\frac{\chi}{10}\big) \big(\frac{\dot{M}_w}{3\times 10^{-6} M_\odot \text{yr}^{-1}}\big)
\big(\frac{\theta_j}{0.1}\big)^2 \big(\frac{v_w}{10^8 \text{cm s}^{-1}}\big)\big(\frac{v_j}{c}\big)^{-1} \text{erg} \, \text{s}^{-1}
(θj0.1)2(vw108cm s−1)(vjc)−1ergs−1\big(\frac{\theta_j}{0.1}\big)^2 \big(\frac{v_w}{10^8 \text{cm s}^{-1}}\big)\big(\frac{v_j}{c}\big)^{-1} \text{erg} \, \text{s}^{-1}

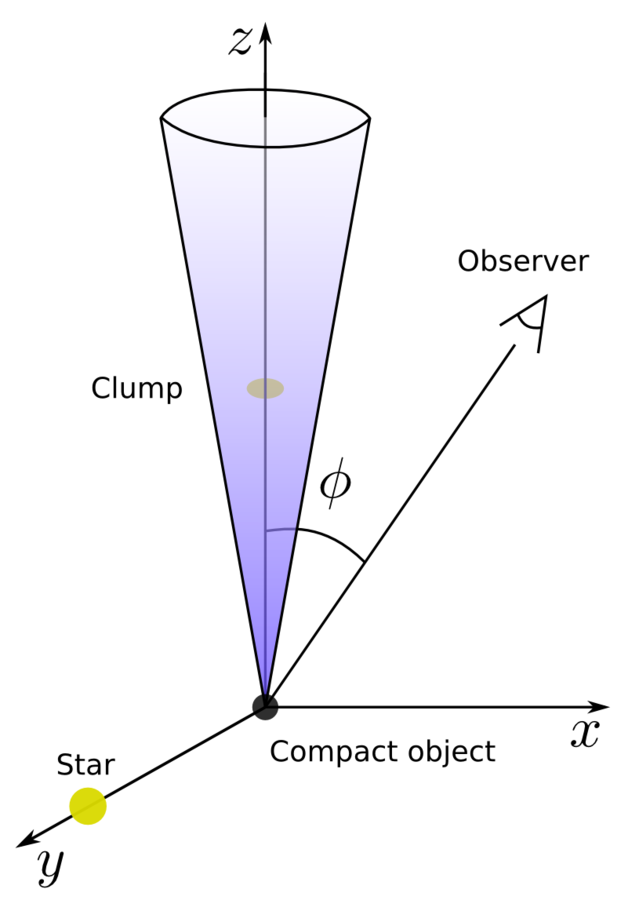
jet opening angle

contrast density

orbital radius

R_{cl}
RclR_{cl}
L_{j}
LjL_{j}

stellar wind speed

jet Lorentz factor

stellar mass-loss rate

\theta_{j}
θj\theta_{j}
\frown
⌢\frown
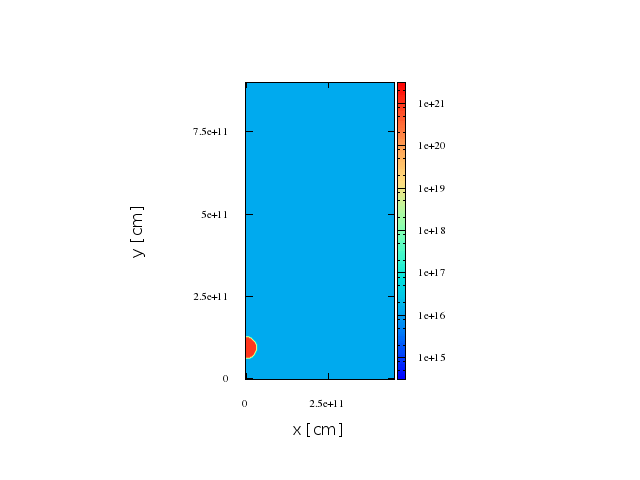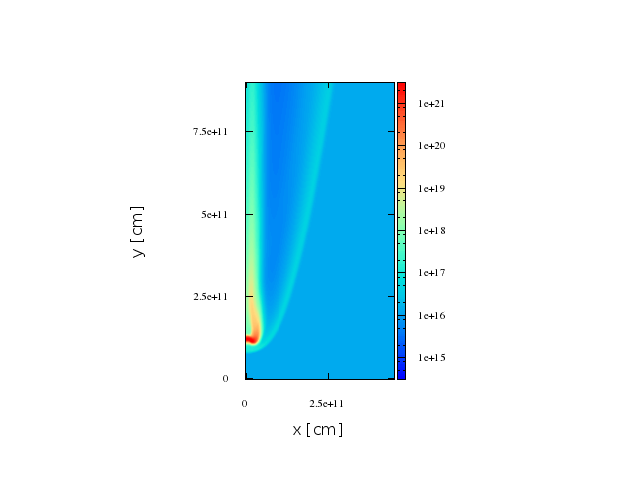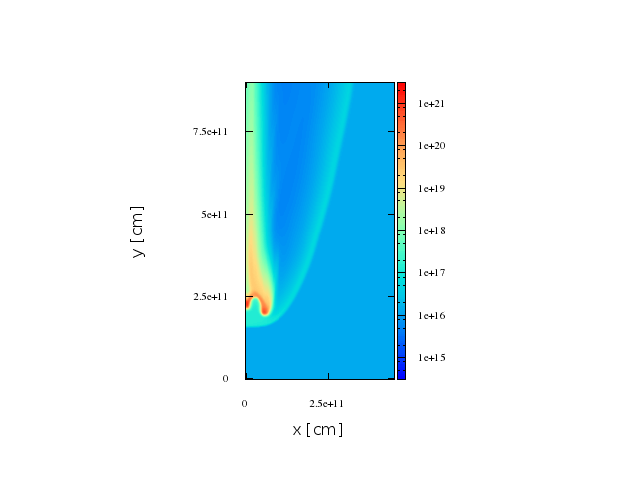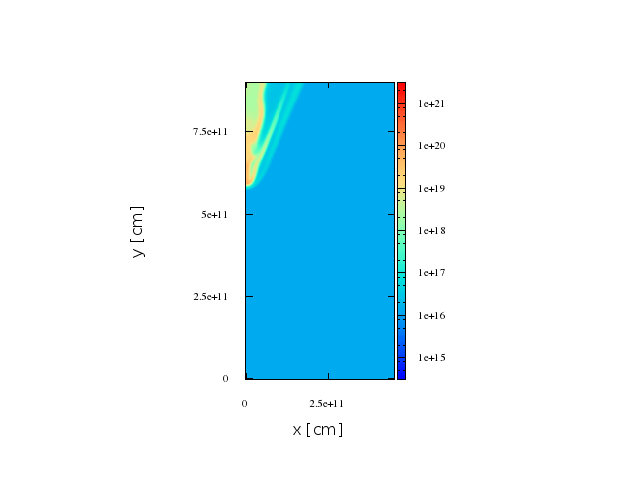
Jet
direction
L_\text{jet} \sim 10^{37}\text{ erg s}^{-1}
Ljet∼1037 erg s−1L_\text{jet} \sim 10^{37}\text{ erg s}^{-1}
\Gamma = 2
Γ=2\Gamma = 2
\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
v⃗stellar wind=2000 km s−1\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
\dot{M}_\star = 3 \times 10^{-6} M_\odot \text{yr}^{-1}
M˙⋆=3×10−6M⊙yr−1\dot{M}_\star = 3 \times 10^{-6} M_\odot \text{yr}^{-1}

O-type Star

x_\star = (-3,-3)\times 10^{12} \mathrm{cm}
x⋆=(−3,−3)×1012cmx_\star = (-3,-3)\times 10^{12} \mathrm{cm}
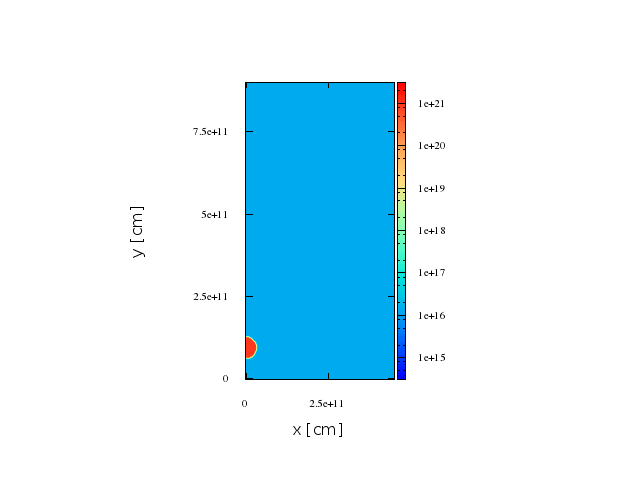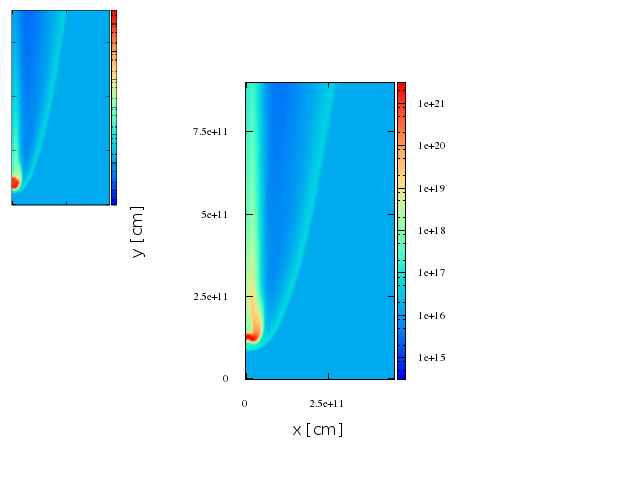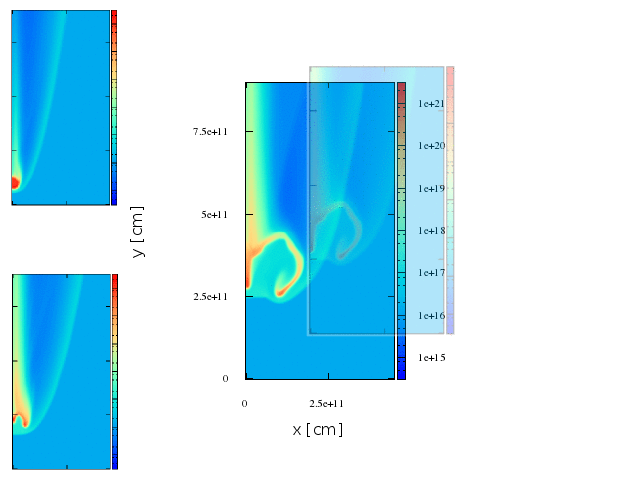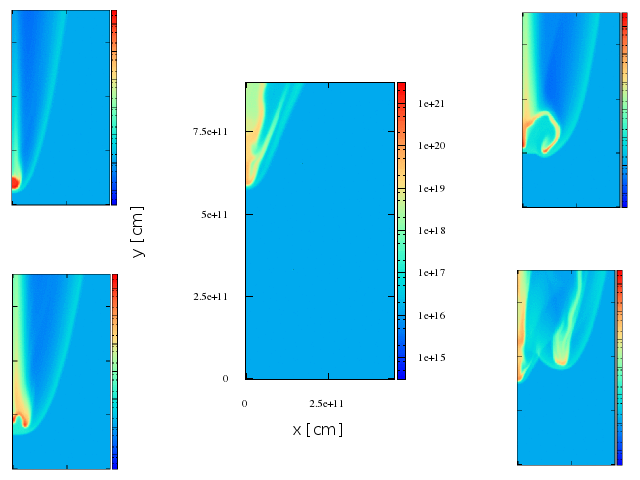
~8.5 min
~1 min
~12 min
~10 min
~14 min
First stage
Second stage

Going into details. hydrodynamic setup.

The fluid is divided in 50 lines with 200 cells each, describing an axisymmetric 2D space of:

r\in[0,4.5]\times10^{11}\text{ cm}
r∈[0,4.5]×1011 cmr\in[0,4.5]\times10^{11}\text{ cm}
y\in[0,9]\times10^{11}\text{ cm}
y∈[0,9]×1011 cmy\in[0,9]\times10^{11}\text{ cm}

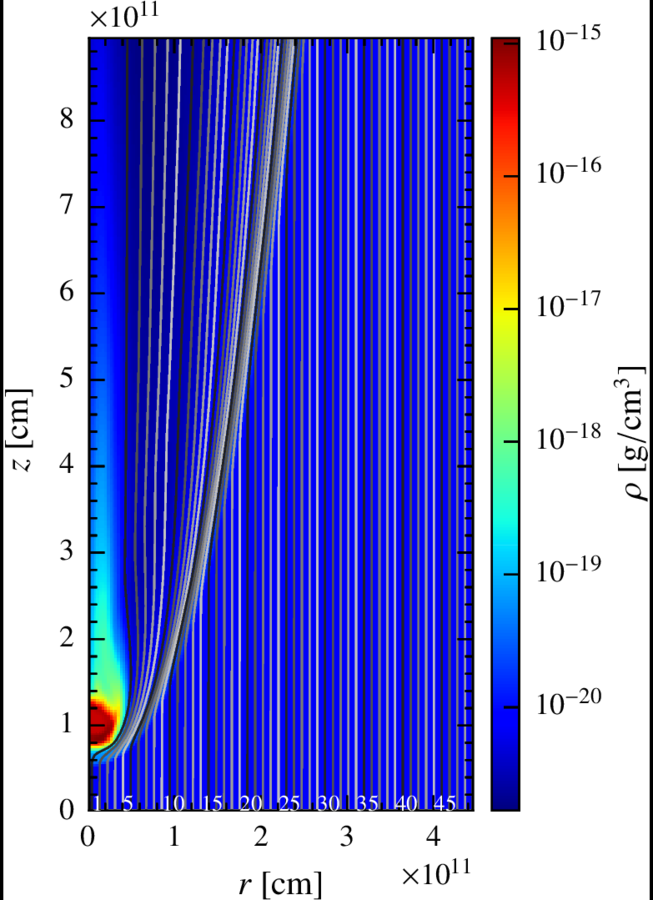
The clump radius, height and density contrast are:

r_{cl}=3\times10^{10}\text{ cm}
rcl=3×1010 cmr_{cl}=3\times10^{10}\text{ cm}
z_{cl}=3\times10^{12}\text{ cm}
zcl=3×1012 cmz_{cl}=3\times10^{12}\text{ cm}
\chi=10
χ=10\chi=10

Half the solar radius

A fifth of an Astronomical Unit

Although the RHD simulation is 2D, we take this information and scramble the different lines around the y axis, giving each cell a random azimuthal angle phi, so the result is more similar to the 3D real scenario.

Going into details. 3d emitter. 

​​de la Cita et al. 2016

Going into details. Physical assumptions.

Magnetic field perpendicular to the fluid line

\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0c^2)
B0′24π=χB(ρ0h0c2)\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0c^2)
B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
Bk′=B0′(ρkv0Γ0ρ0vkΓk)1/2B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
\chi_B = 10^{-4}, 1
χB=10−4,1\chi_B = 10^{-4}, 1

Definition of the magnetic field at the beginning of the line:

Evolution of the B field in the different cells k:

(Low, high magnetic field)

Fraction of matter energy flux that goes to magnetic energy

Photon field:

T_{\star} = 4\times 10^4 \text{ K}
T⋆=4×104 KT_{\star} = 4\times 10^4 \text{ K}
L_{\star} = 1\times 10^{39} \text{erg s}^{-1}
L⋆=1×1039erg s−1L_{\star} = 1\times 10^{39} \text{erg s}^{-1}

injection of non-thermal particles

A fraction of the generated internal energy per second in the cell k enters in the form of non-thermal particles.

\chi = 0.1
χ=0.1\chi = 0.1

Biggest uncertainty

Going into details. Observer angle.

To get a feeling of the importance of the observer angle, we have chosen the following angles:

  • 0º - with the jet pointing at the observer
  • 30º - representative of Cygnus X-1
  • 90º - the observer is placed in the x axis

The observer will be placed in the x axis forming an angle phi with the vertical axis. 

\phi = 0^\circ, 30^\circ, 90^\circ
ϕ=0∘,30∘,90∘\phi = 0^\circ, 30^\circ, 90^\circ

Going into details. some notes on the code.

  1. We let the particles evolve until they reach a steady state so we can consider the medium stationary, in other words, every loss time (e.g. synchrotron) or cell-crossing time is much shorter than the dynamical time on large scales. Described in de la Cita et al.  '16.

  2. All the computation is done in the (relativistic) frame of the fluid, so every relevant quantity has to be transformed, including the angles between fluid, gamma photons and target photons velocities.

  3. Once we have the electron distribution, we compute the inverse Compton (IC) and synchrotron radiation, taking into account the Doppler boosting.

\delta = 1/\Gamma(1-\beta\cos{\theta_\text{obs}})
δ=1/Γ(1−βcosθobs)\delta = 1/\Gamma(1-\beta\cos{\theta_\text{obs}})
\epsilon L(\epsilon)= \delta^4\epsilon'L'(\epsilon')
ϵL(ϵ)=δ4ϵ′L′(ϵ′)\epsilon L(\epsilon)= \delta^4\epsilon'L'(\epsilon')

where

Results. First case, smaller shocked region

In the case of a low magnetic field, the IC radiation dominates the spectrum.

The difference between the three angles come from the doppler boosting, more important for smaller angles given that most of the cells have a strong z- component of the  velocity

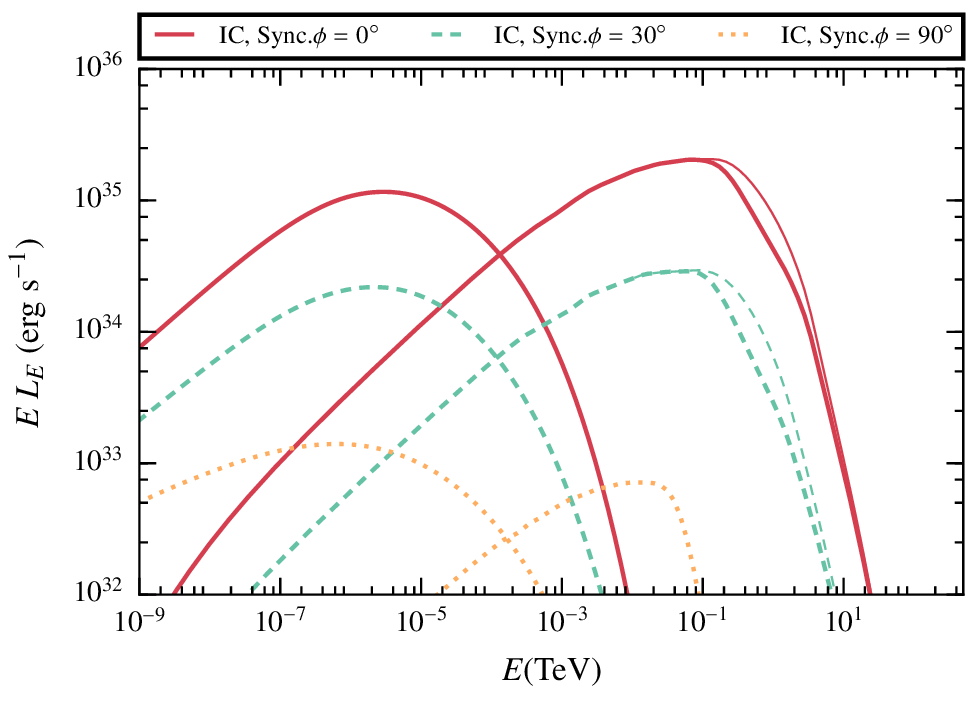
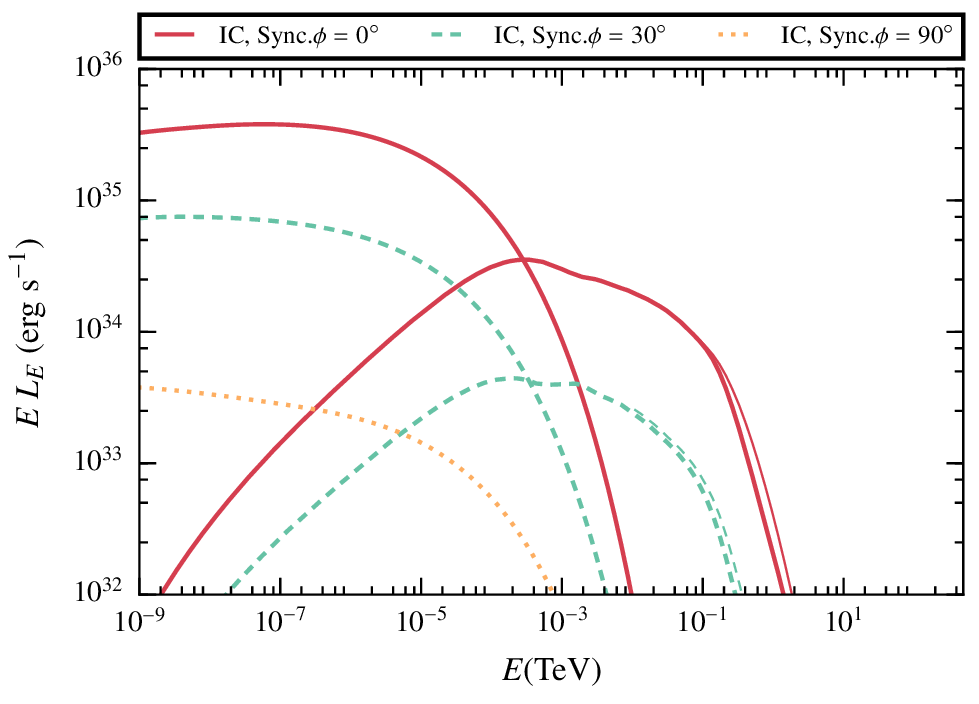
Low B

High B

\chi_B = 10^{-4}
χB=10−4\chi_B = 10^{-4}
\chi_B = 1
χB=1\chi_B = 1
10^{35} \text{ erg s}^{-1}
1035 erg s−110^{35} \text{ erg s}^{-1}

Low B

High B

\chi_B = 10^{-4}, \phi = 30^\circ
χB=10−4,ϕ=30∘\chi_B = 10^{-4}, \phi = 30^\circ
\chi_B = 1, \phi = 30^\circ
χB=1,ϕ=30∘\chi_B = 1, \phi = 30^\circ

Results. comparison between the two cases.

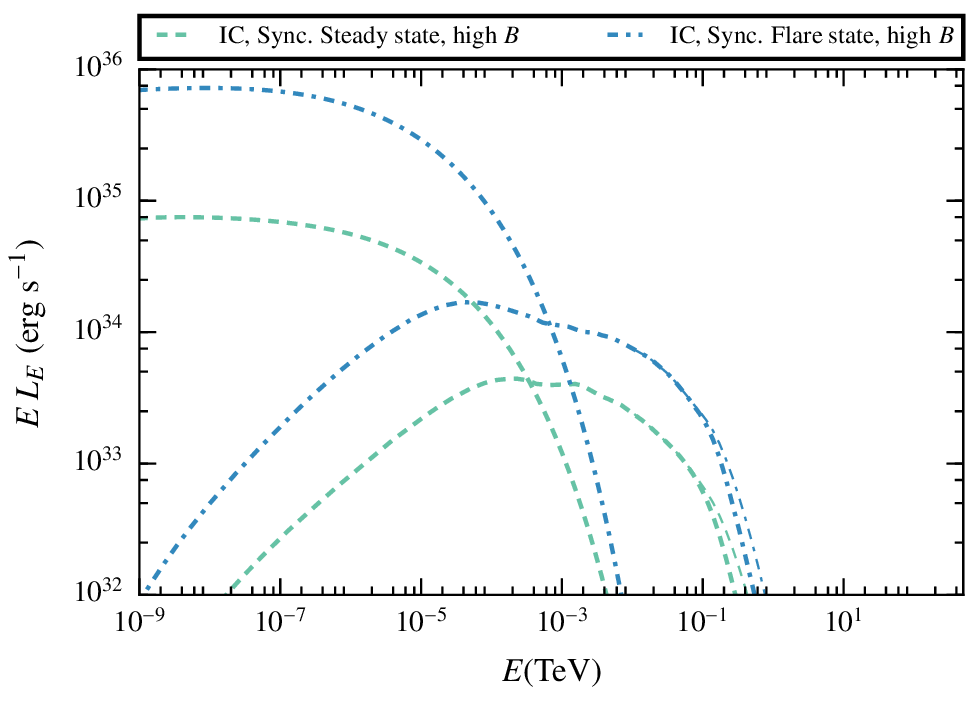
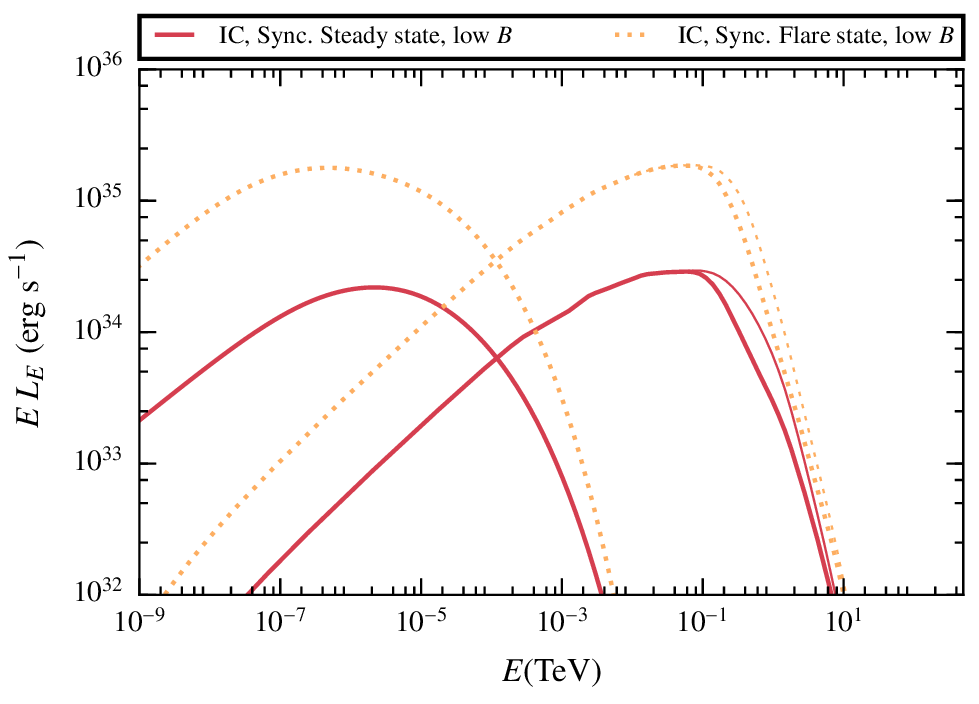
In general the non-thermal radiation will be increased for larger shocks, produced while the clumps is being disrupted.

Results. Duty cycle and standing luminosity.

L_\text{GeV}\approx 10^{35} \text{ erg s}^{-1}
LGeV≈1035 erg s−1L_\text{GeV}\approx 10^{35} \text{ erg s}^{-1}

Knowing the lifetime of a clump inside the jet and the frequency they enter with (for a given clump size) we can compute the duty cycle (DC): the fraction of the time that a certain type of clumps are interacting with the jet.

For a wide variety of parameters we obtain a duty cycle of 1, meaning there is about one clump interacting with the jet at every time .

Cygnus X-1:

Cygnus X-3:

\chi \sim 0.01
χ∼0.01\chi \sim 0.01
\chi \sim 0.1
χ∼0.1\chi \sim 0.1
DC \sim 1
DC∼1DC \sim 1

Conclusions.

  • The effective radius of the emitter is much bigger than the clump radius. Emission levels strongly depend on the viewer angle due to Doppler boosting.

  • Depending on the duty cycle and the mass distribution of clumps, their radiation can contribute to either the standing high-energy emission.

  • ...and also be responsible of short GeV flares,   like those observed by AGILE in Cygnus X-1 (Sabatini et al. '10).

eskerrik asko.

backup slide. Physical assumptions.

We follow a prescription for particle acceleration in strong shocks. The acceleration timescale  goes like ~1/v² as proposed in previous works (e.g. Drury 1983)

We inject non-thermal particles when a shock takes place:

Internal energy goes up

and

fluid velocity goes down

Where and how do we inject non-thermal particles

Q(E) \propto E^{-2} \times (e^{-E_{min}/E})^5 \times e^{-E/E_{max}}
Q(E)∝E−2×(e−Emin/E)5×e−E/EmaxQ(E) \propto E^{-2} \times (e^{-E_{min}/E})^5 \times e^{-E/E_{max}}
t'_\text{acc}=\eta E'qB'c, \text{with}
tacc′=ηE′qB′c,witht'_\text{acc}=\eta E'qB'c, \text{with}
\eta = 2\pi (c/v)^2
η=2π(c/v)2\eta = 2\pi (c/v)^2

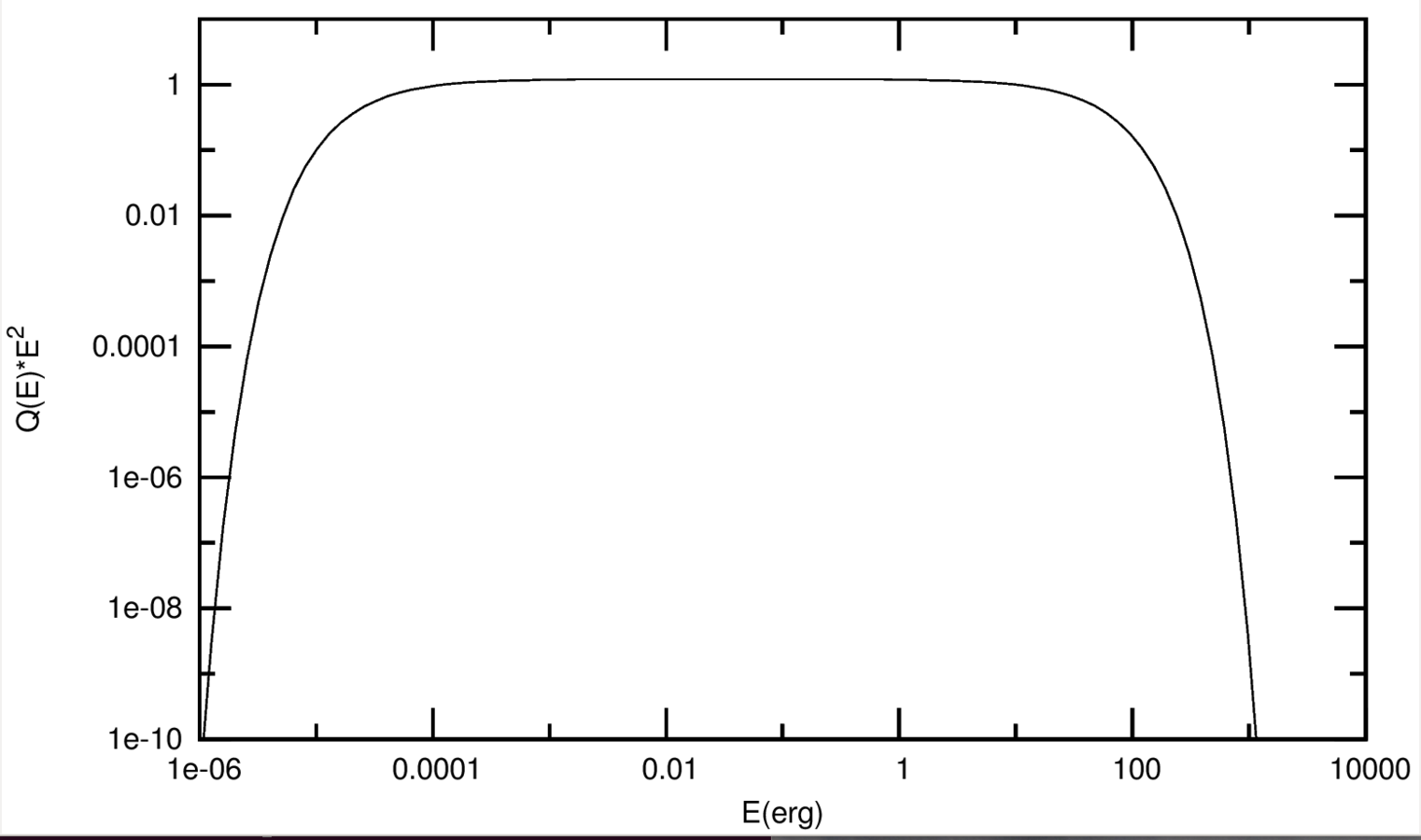
Backup slide. Fixing the line ending.

Given that the two winds can mix through the fluid lines, we have had to cut the lines at a certain point. To do so, we can impose that the amount of material that crosses the section do not get larger than a certain threshold:

\text{if: } S\rho v\Gamma > 2\times S_0\rho_0v_0\,\rightarrow\, \text{end of the line}
if: SρvΓ>2×S0ρ0v0→end of the line\text{if: } S\rho v\Gamma > 2\times S_0\rho_0v_0\,\rightarrow\, \text{end of the line}

Backup slide. Injected Luminosity.

The injected non-thermal particles have a lumisosity given by a fraction of the generated internal energy per second in the cell.

L_{inj} = \chi_{NT} \times \dot{U}'_k =
Linj=χNT×U˙k′=L_{inj} = \chi_{NT} \times \dot{U}'_k =

With the pre-factor varying between 0 and 1 and the +/- subindexes refering to the right/left boundaries, respectively.

= \chi_{NT} v_k\Gamma_k^2\times \left(S_+\Gamma_+^2h_+\rho_+c^2\left(1 +\dfrac{v_+^2}{c^2}\right) - S_-\Gamma_-^2h_-\rho_-c^2\left(1 +\dfrac{v_-^2}{c^2}\right)\right)
=χNTvkΓk2×(S+Γ+2h+ρ+c2(1+v+2c2)−S−Γ−2h−ρ−c2(1+v−2c2))= \chi_{NT} v_k\Gamma_k^2\times \left(S_+\Gamma_+^2h_+\rho_+c^2\left(1 +\dfrac{v_+^2}{c^2}\right) - S_-\Gamma_-^2h_-\rho_-c^2\left(1 +\dfrac{v_-^2}{c^2}\right)\right)
Made with Slides.com