Contribution due to clumpy winds to the gamma-ray emission in microquasar jets

s. del palacio, v. bosch-ramon, X. paredes-fortuny, g. e. romero,

D. khangulyan and M. ribó

Cargese, 26th May 2016

V. M. DE LA CITA

high-mass Microquasars (HMMQ)
A story of clumpy winds

Within the textbook picture of an x-ray binary, the donor star transfers matter to the compact object, forming an accretion disk around it and, in the case of microquasars, two bipolar relativistic outflows (our beloved jets).

In the specific case of  a high-mass microquasar, the winds of the (massive) donor star are expected to be strongly inhomogeneous (e.g. Owocki & Cohen '06, Moffat '08), presenting overdensities (clumps) that may interact with the jet.

physical scenario

The impact of clump-like wind inhomogeneities on the jets of microquasars has been addressed in a more analytical way by Araudo et al. '09 and Perucho et al. '12 performed a detailed three-dimensional simulations. 

Here we couple for the first time relativistic hydrodynamical (RHD) simulations with non-thermal radiative calculations, along with a semi-analytical description of the frequency and characteristics of this jet-clumps interactions.

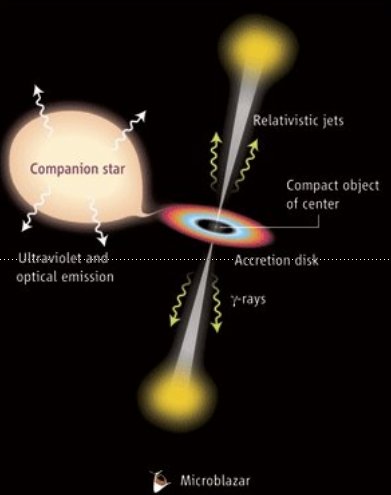
​​Credit: F. Mirabel
Jet
direction
L_\text{jet} \sim 10^{37}\text{ erg s}^{-1}
Ljet∼1037 erg s−1L_\text{jet} \sim 10^{37}\text{ erg s}^{-1}
\Gamma = 2
Γ=2\Gamma = 2
\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
v⃗stellar wind=2000 km s−1\vec{v}_\text{stellar wind} = 2000 \text{ km s}^{-1}
\dot{M}_\star = 3 \times 10^{-6} M_\odot \text{yr}^{-1}
M˙⋆=3×10−6M⊙yr−1\dot{M}_\star = 3 \times 10^{-6} M_\odot \text{yr}^{-1}

O-type Star

(far away)

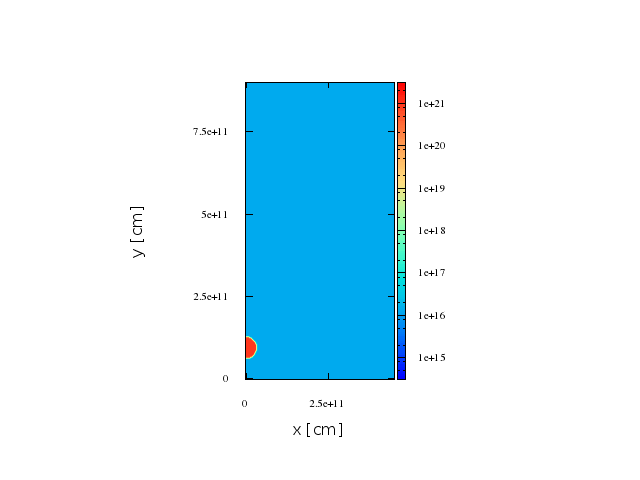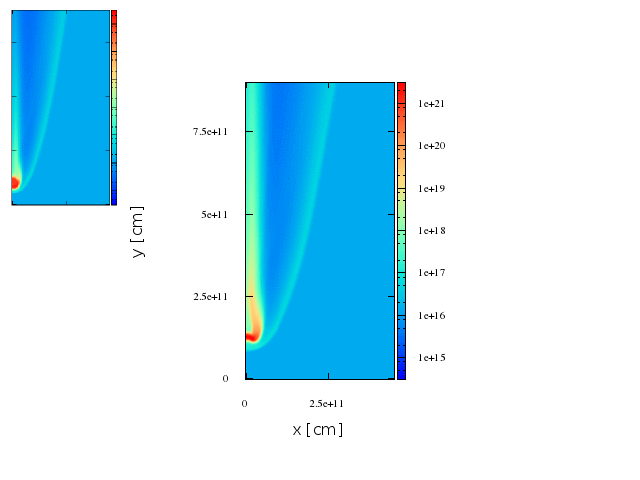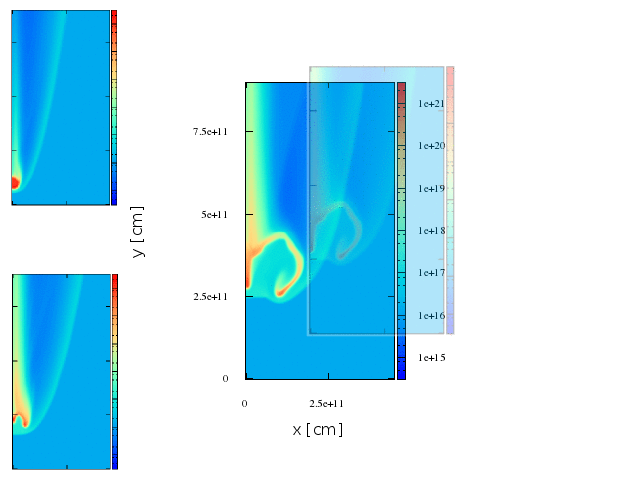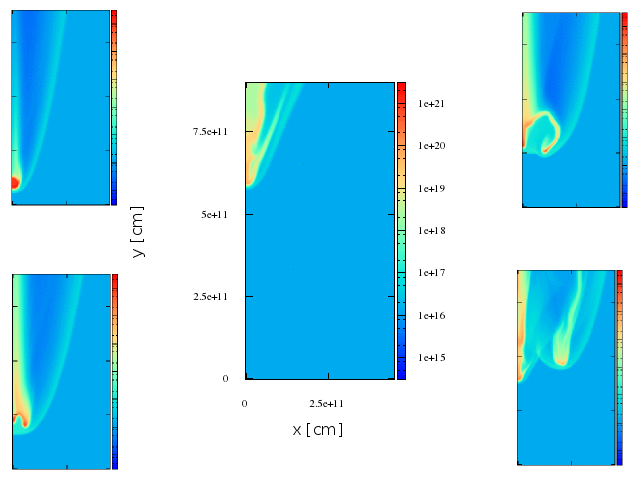
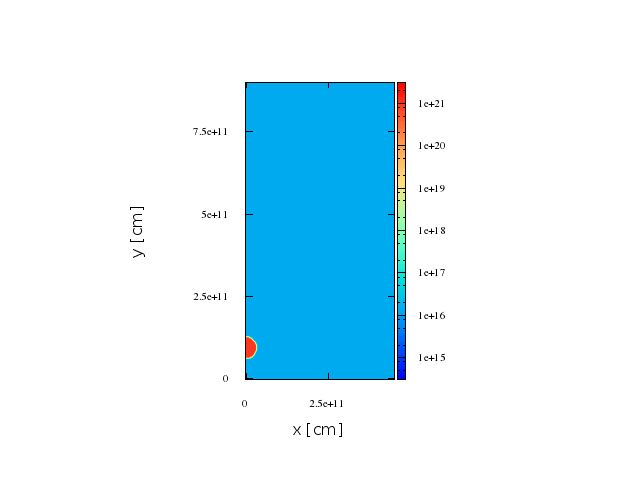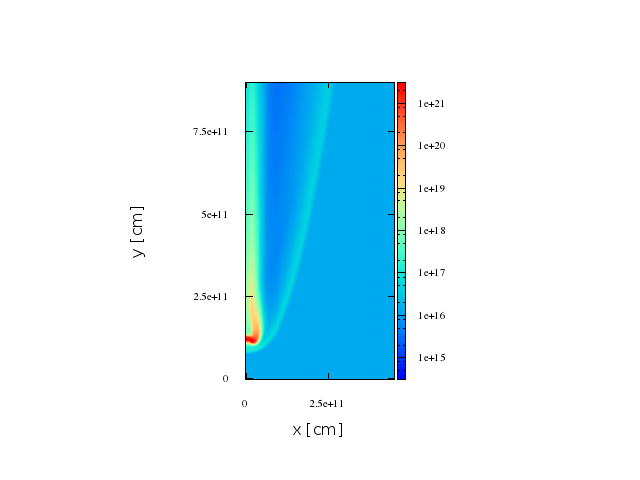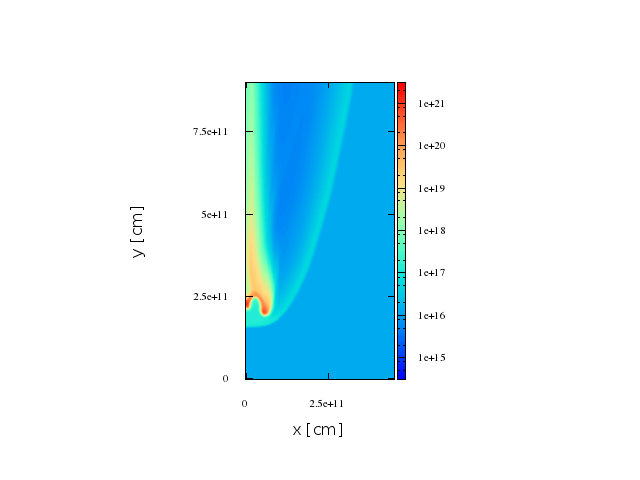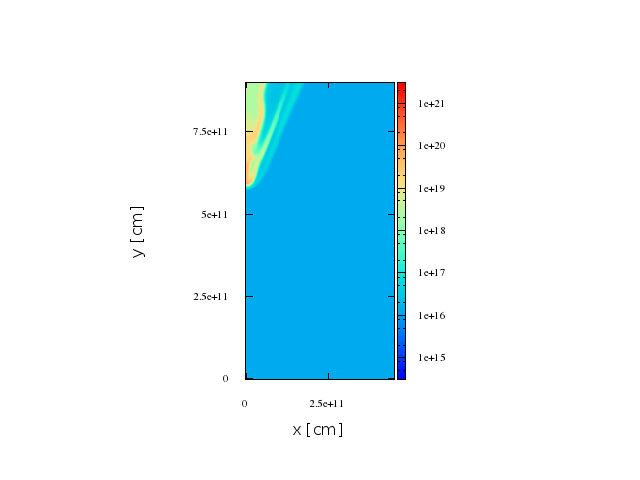
~8.5 min
~1 min
~12 min
~10 min
~14 min
First stage
Second stage

Going into details. hydrodynamic setup.

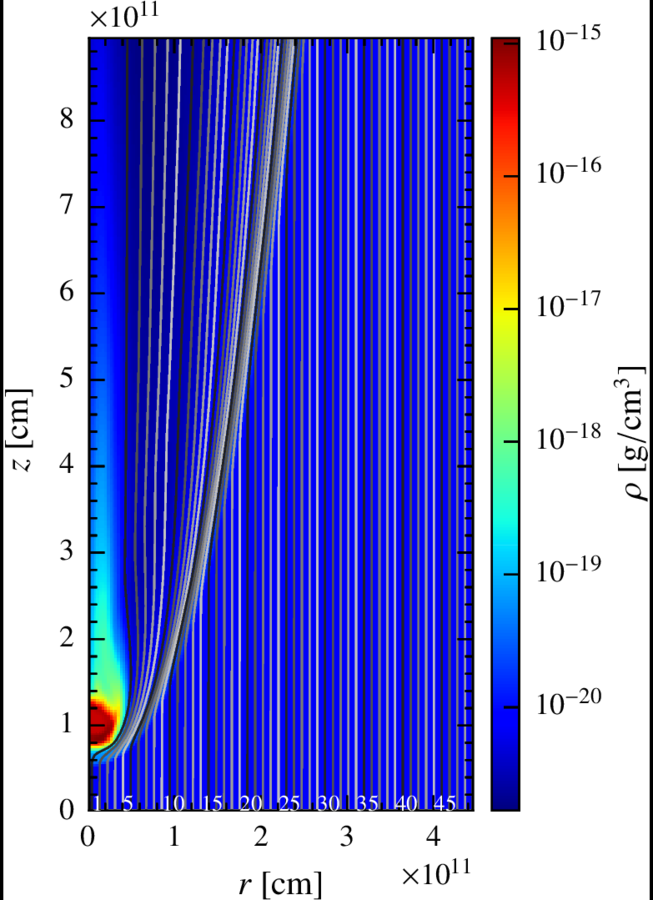
The fluid is divided in 50 lines with 200 cells each, describing an axisymmetric 2D space of:

r\in[0,4.5\times10^{11}\text{ cm}]
r∈[0,4.5×1011 cm]r\in[0,4.5\times10^{11}\text{ cm}]
y\in[0,9\times10^{11}\text{ cm}]
y∈[0,9×1011 cm]y\in[0,9\times10^{11}\text{ cm}]

The clump radius, height and density contrast are:

r_{cl}=3\times10^{10}\text{ cm}
rcl=3×1010 cmr_{cl}=3\times10^{10}\text{ cm}
z_{cl}=3\times10^{12}\text{ cm}
zcl=3×1012 cmz_{cl}=3\times10^{12}\text{ cm}
\chi=10
χ=10\chi=10

HALF the solar radius!

A FOURTH of an Astronomical Unit!

Although the RHD simulation is 2D, we take this information and scramble the different lines around the y axis, giving each cell a random azimuthal angle phi, so the result is more similar to the 3D real scenario.

Going into details. 3d emitter.

Going into details. Physical assumptions.

Magnetic field perpendicular to the fluid line

\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0c^2)
B0′24π=χB(ρ0h0c2)\dfrac{B_0^{\prime 2}}{4\pi} = \chi_B (\rho_0h_0c^2)
B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
Bk′=B0′(ρkv0Γ0ρ0vkΓk)1/2B_k^\prime = B_0^\prime \Big( \dfrac{\rho_k v_0\Gamma_0}{\rho_0 v_k \Gamma_k}\Big)^{1/2}
\chi_B = 10^{-4}, 1
χB=10−4,1\chi_B = 10^{-4}, 1

Definition of the magnetic field at the beginning of the line:

Evolution of the B field in the different cells k:

(Low, high magnetic field)

Fraction of matter energy flux that goes to magnetic energy

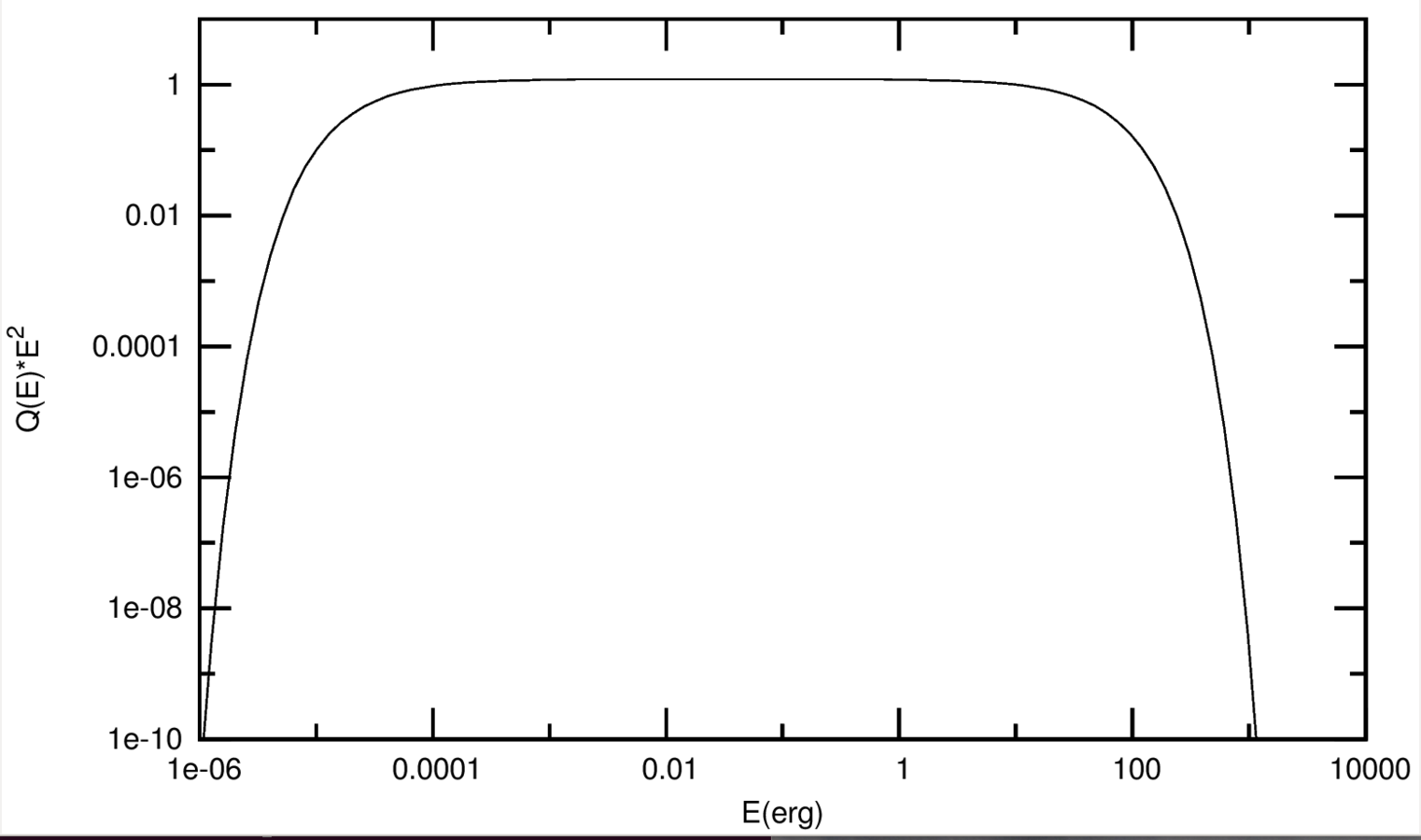
Photon field:

T_{\star} = 4\times 10^4 \text{ K}
T⋆=4×104 KT_{\star} = 4\times 10^4 \text{ K}
L_{\star} = 1\times 10^{39} \text{erg s}^{-1}
L⋆=1×1039erg s−1L_{\star} = 1\times 10^{39} \text{erg s}^{-1}

injection of non-thermal particles

A fraction of the generated internal energy per second in the cell k enters in the form of non-thermal particles.

\chi = 0.1
χ=0.1\chi = 0.1

Going into details. some notes on the code.

  1. We let the particles evolve until they reach a steady state so we can consider the medium stationary, in other words, every loss time (e.g. synchrotron) or cell-crossing time is much shorter than the dynamical time on large scales. Described in de la Cita et al  '16.

  2. All the computation is done in the (relativistic) frame of the fluid, so every relevant quantity has to be transformed, including the angles between fluid, gamma photons and target photons velocities.

  3. Once we have the electron distribution, we compute the inverse Compton (IC) and synchrotron radiation, taking into account the Doppler boosting.

\delta = 1/\Gamma(1-\beta\cos{\theta_\text{obs}})
δ=1/Γ(1−βcosθobs)\delta = 1/\Gamma(1-\beta\cos{\theta_\text{obs}})
\epsilon L(\epsilon)= \delta^4\epsilon'L(\epsilon')
ϵL(ϵ)=δ4ϵ′L(ϵ′)\epsilon L(\epsilon)= \delta^4\epsilon'L(\epsilon')

where

Ghisellini's talk

Going into details. Physical assumptions i.

We follow a prescription for particle acceleration in strong shocks. The acceleration timescale  goes like ~1/v² as proposed in previous works (e.g. Drury 1983)

We inject non-thermal particles when a shock takes place:

Internal energy goes up

and

fluid velocity goes down

Where and how do we inject non-thermal particles

Q(E) \propto E^{-2} \times (e^{-E_{min}/E})^5 \times e^{-E/E_{max}}
Q(E)∝E−2×(e−Emin/E)5×e−E/EmaxQ(E) \propto E^{-2} \times (e^{-E_{min}/E})^5 \times e^{-E/E_{max}}
t'_\text{acc}=\eta E'qB'c, \text{with}
tacc′=ηE′qB′c,witht'_\text{acc}=\eta E'qB'c, \text{with}
\eta = 2\pi (c/v)^2
η=2π(c/v)2\eta = 2\pi (c/v)^2

Going into details. Observer angle.

To get a feeling of the importance of the observer angle, we have chosen the most extremes angles: 0º (with the jet bulk velocity pointing at the observer),  and 90º (when the observer is placed in the z axis).

The observer will be placed beyond the star forming an angle theta with the vertical axis. 

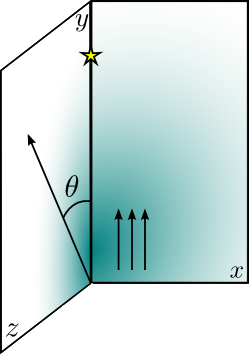
Clump

Jet thrust

\theta = 0^\circ, 90^\circ
θ=0∘,90∘\theta = 0^\circ, 90^\circ

Results. First case, smaller shocked region

In the case of a low magnetic field, the IC radiation dominates the spectrum.

The difference between the two angles come from the doppler boosting, more important for smaller angles given that most of the cells have a strong z- component of the  velocity

Results. second case, bigger shocked region

Results. comparison between the two cases.

In general the non-thermal radiation will be increased for larger shocks, produced while the clumps is being disrupted, specially when looking at the system off the head-on  direction. When looking from this directions the pair-creation absorption is more important due to the geometry of the system.

Maps. 2d axisymmetric representation.

We have built maps to have a sense of where the radiation comes from. It is important to recall that this maps are a 2D representation of a 3D shock. 

Maps. FIrst stage.

Inverse compton

synchrotron

\chi_B = 10^{-4},\,\,\theta = 0^\circ
χB=10−4,θ=0∘\chi_B = 10^{-4},\,\,\theta = 0^\circ

The total observer luminosity in this case is:

L_{IC+sync}\approx 2.5 \times 10^{35} \text{erg s}^{-1}
LIC+sync≈2.5×1035erg s−1L_{IC+sync}\approx 2.5 \times 10^{35} \text{erg s}^{-1}

While in the fluid frame the total luminosity is:

L_{IC+sync}\approx 1.5 \times 10^{37} \text{erg s}^{-1}
LIC+sync≈1.5×1037erg s−1L_{IC+sync}\approx 1.5 \times 10^{37} \text{erg s}^{-1}

Maps. second stage.

Inverse compton

synchrotron

\chi_B = 10^{-4},\,\,\theta = 0^\circ
χB=10−4,θ=0∘\chi_B = 10^{-4},\,\,\theta = 0^\circ

The total observer luminosity in this case is:

L_{IC+sync}\approx 2.2 \times 10^{36} \text{erg s}^{-1}
LIC+sync≈2.2×1036erg s−1L_{IC+sync}\approx 2.2 \times 10^{36} \text{erg s}^{-1}

While in the fluid frame the total luminosity is:

L_{IC+sync}\approx 4.5 \times 10^{37} \text{erg s}^{-1}
LIC+sync≈4.5×1037erg s−1L_{IC+sync}\approx 4.5 \times 10^{37} \text{erg s}^{-1}

Discussion. Generalization of the results.

R_{cl} > 3\times10^{10} \left(\frac{\eta_{j}}{0.1}\right) \left(\frac{10}{\chi}\right) \left(\frac{R_{orb}}{3\times10^{12}\mathrm{cm}}\right) \mathrm{cm}
Rcl>3×1010(ηj0.1)(10χ)(Rorb3×1012cm)cmR_{cl} > 3\times10^{10} \left(\frac{\eta_{j}}{0.1}\right) \left(\frac{10}{\chi}\right) \left(\frac{R_{orb}}{3\times10^{12}\mathrm{cm}}\right) \mathrm{cm}
L_{j} < 0.25 (1-1/\gamma_{j}) \, \chi \dot{M}_{w} c^2 \eta_{j}^2 (v_{w} / v_{j})
Lj<0.25(1−1/γj)χM˙wc2ηj2(vw/vj)L_{j} < 0.25 (1-1/\gamma_{j}) \, \chi \dot{M}_{w} c^2 \eta_{j}^2 (v_{w} / v_{j})

The minimum radius for a clump to enter the jet is:

L_j<1.6\times 10^{37}\mathrm{erg}\,\mathrm s^{-1}
Lj<1.6×1037ergs−1L_j<1.6\times 10^{37}\mathrm{erg}\,\mathrm s^{-1}

with

The maximum jet luminosity not to destroy the jet before it enters:

which in the case of Cygnus X1 this gives rise to 

\eta_j=R_j/z_j
ηj=Rj/zj\eta_j=R_j/z_j

Knowing the lifetime of a clump inside the jet and the frequency they enter with (for a given clump size) we can compute the duty cycle: the fraction of the time that a certain type of clumps are interacting with the jet.

Discussion. Conclusions.

  • The effective radius of the emitter is much bigger than the clump radius. 

  • Emission levels strongly depend on the viewer angle due to Doppler boosting.

  • Depending on the duty cycle and the mass distribution of clumps, their radiation can contribute to the standing high-energy emission and also be responsible of short GeV flares,   like those observed by AGILE in Cygnus X-1 (Sabatini et al. '10).

Thank You.

"Science is a wonderful thing if one does not have to earn one's living at it."
A. Einstein

Backup slide. Fixing the line ending.

Given that the two winds can mix through the fluid lines, we have had to cut the lines at a certain point. To do so, we can impose that the amount of material that crosses the section do not get larger than a certain threshold:

\text{if: } S\rho v\Gamma > 2\times S_0\rho_0v_0\,\rightarrow\, \text{end of the line}
if: SρvΓ>2×S0ρ0v0→end of the line\text{if: } S\rho v\Gamma > 2\times S_0\rho_0v_0\,\rightarrow\, \text{end of the line}

Backup slide. Injected Luminosity.

The injected non-thermal particles have a lumisosity given by a fraction of the generated internal energy per second in the cell.

L_{inj} = \chi_{NT} \times \dot{U}'_k =
Linj=χNT×U˙k′=L_{inj} = \chi_{NT} \times \dot{U}'_k =

With the pre-factor varying between 0 and 1 and the +/- subindexes refering to the right/left boundaries, respectively.

= \chi_{NT} v_k\Gamma_k^2\times \left(S_+\Gamma_+^2h_+\rho_+c^2\left(1 +\dfrac{v_+^2}{c^2}\right) - S_-\Gamma_-^2h_-\rho_-c^2\left(1 +\dfrac{v_-^2}{c^2}\right)\right)
=χNTvkΓk2×(S+Γ+2h+ρ+c2(1+v+2c2)−S−Γ−2h−ρ−c2(1+v−2c2))= \chi_{NT} v_k\Gamma_k^2\times \left(S_+\Gamma_+^2h_+\rho_+c^2\left(1 +\dfrac{v_+^2}{c^2}\right) - S_-\Gamma_-^2h_-\rho_-c^2\left(1 +\dfrac{v_-^2}{c^2}\right)\right)
Made with Slides.com