卷積
by 不卷王
卷積
by 不卷王
今天沒有偷簡報環節了吧(?
今天會講到
- FFT
- NTT
- 迭代式FFT/NTT
- 任意模數FFT
- FWHT
講師不像你們那麼卷，我最近才初學一點點卷積
講很爛很不嚴謹請見諒
然後因為我進度燒雞，所以沒有放例題，這堂課就是來看我假裝會卷積
如果覺得我的code太醜的話，我只能說學長對不起
野獸 先備
矩陣
$$\begin{bmatrix}a&b\\c&d\end{bmatrix}\times \begin{bmatrix}e&f\\g&h\end{bmatrix}=\begin{bmatrix}ae+bg&af+bh\\ce+dg&cf+dh\end{bmatrix}$$
複數
$$i^2=-1$$
$$(a+bi)\times (c+di)=ac+(ad+bc)i-bd$$
歐拉公式
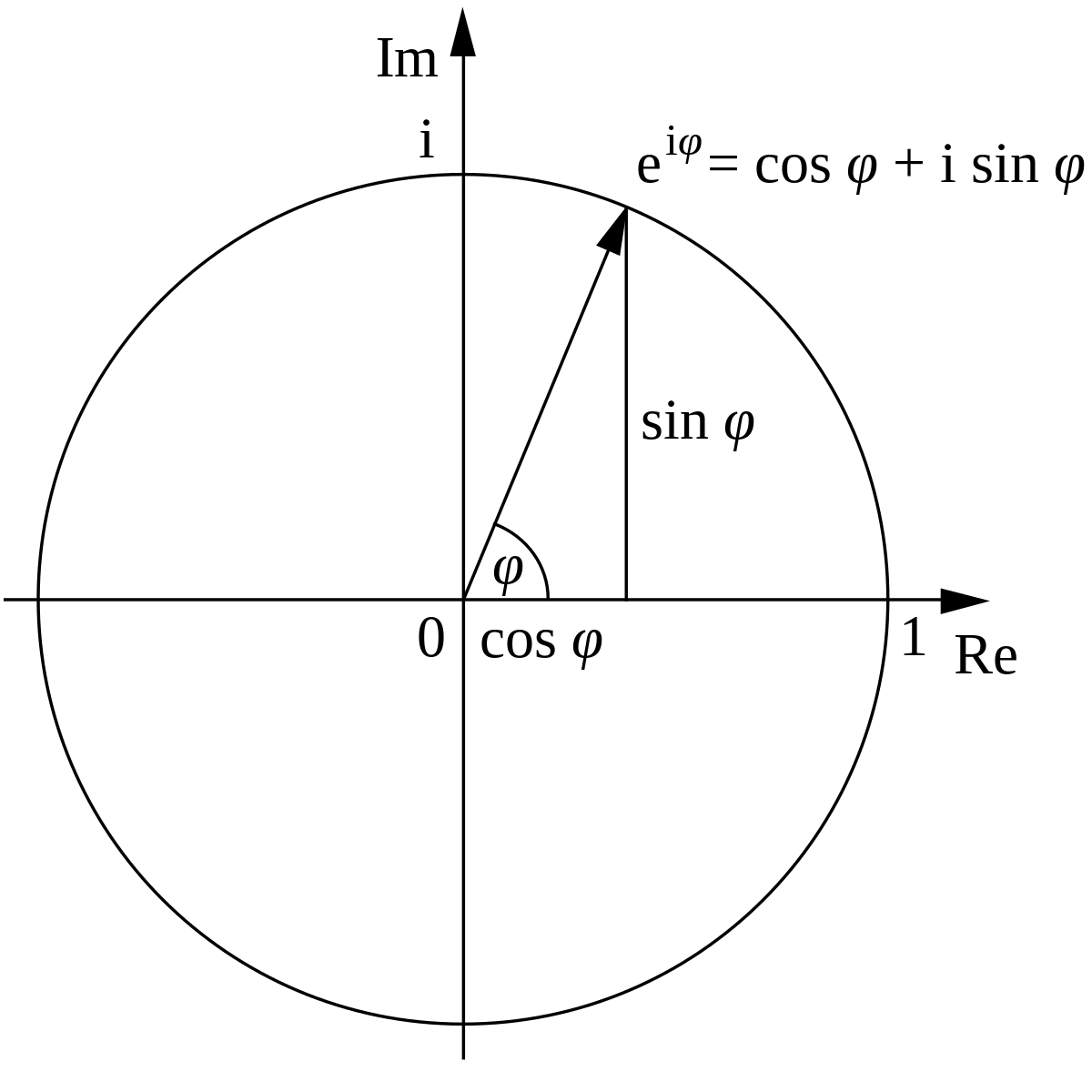
棣美弗公式
- \( (cos\theta + i\ sin\theta)n = cos(n\theta) + i\ sin(n\theta)\)
- 用歐拉公式來看的話根本是廢話 : \((e^{i\theta})^n=e^{in\theta}\)
單位根
- \((\omega_{n})^n=1\)
- \(x^n=1\)的根分別為\(1,\omega_{n},\cdots,\omega_{n}^{n-1}\)
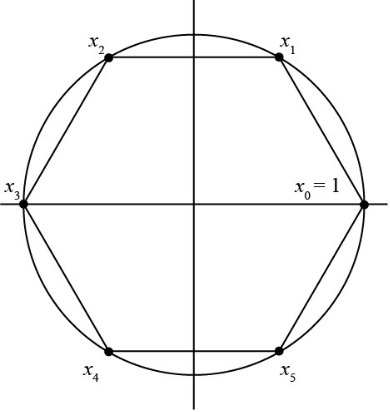
$$\omega_6^3$$
$$\omega_6^2$$
$$\omega_6$$
$$\omega_6^0$$
$$\omega_6^4$$
$$\omega_6^4$$
$$\omega_6^5$$
.
原根
其實我不會ㄟ
$$(M)$$
原根
質數\(P\)以下的原根\(g\)的\(1\)次方到\(P-1\)次方，恰好對到\(1\sim P-1\)的每個數
模\(7\)之下，\(3\)是，\(2\)不是
$$3^1\equiv 3, 3^2 \equiv 2,3^3 \equiv 6,3^4\equiv 4,3^5\equiv5,3^6=1$$
$$2^1\equiv 2, 2^2 \equiv 4,2^3 \equiv 1$$
約定
- 多項式\(A\)、\(B\)、\(C=A\times B\)皆為整係數多項式
- \(C\)有\(n\)項(最高次數為\(n-1\))
- \(A,B\)的最高次數\(<\frac{n}{2}\)，自動補0在後面到\(n項\)
- \(n\)為\(2^k\)，\(k\)為整數
約定
- 多項式\(A\)、\(B\)、\(C=A\times B\)皆為整係數多項式
- \(C\)有\(n\)項(最高次數為\(n-1\))
- \(A,B\)的最高次數\(<\frac{n}{2}\)，自動補0在後面到\(n項\)
- \(n\)為\(2^k\)，\(k\)為整數
$$a_0 x_0 + a_1 x_1+\cdots+a_{\frac{n}{2}-1}x_{\frac{n}{2}-1}$$
約定
- 多項式\(A\)、\(B\)、\(C=A\times B\)皆為整係數多項式
- \(C\)有\(n\)項(最高次數為\(n-1\))
- \(A,B\)的最高次數\(<\frac{n}{2}\)，自動補0在後面到\(n項\)
- \(n\)為\(2^k\)，\(k\)為整數
$$a_0 x_0 + a_1 x_1+\cdots+a_{\frac{n}{2}-1}x_{\frac{n}{2}-1}+0+0+\cdots+0$$
$$\frac{n}{2}個$$
$$a_0 x_0 + a_1 x_1+\cdots+a_{\frac{n}{2}-1}x_{\frac{n}{2}-1}$$
FFT
FFT想要解決什麼?
- 快速地把兩個多項式乘起來
- 直接乘起來\(O(n^2)\)
FFT想要解決什麼?
- 快速地把兩個多項式乘起來
- 直接乘起來\(O(n^2)\)
- 如果帶入固定的\(n\)個\(x\)取樣的話，乘法就變\(O(n)\)，
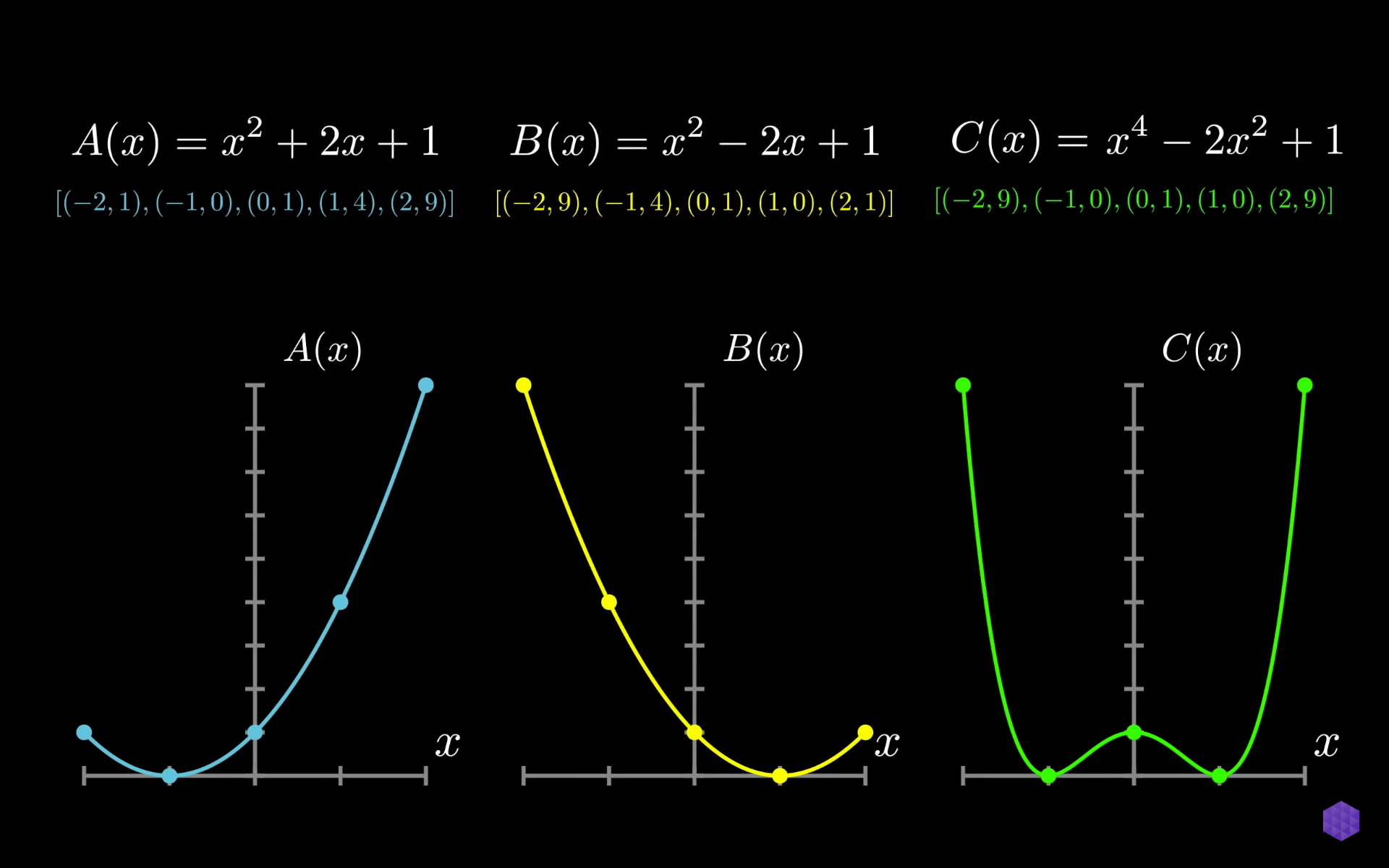
FFT想要解決什麼?
- 快速地把兩個多項式乘起來
- 直接乘起來\(O(n^2)\)
- 如果用取樣的話，乘法就變\(O(n)\)
- 要怎麼快速把\(n\)個點帶入? 暴力\(O(n^2)\)
- 要怎麼轉換回來? 拉格朗日插值要\(O(n^2)\)
是否可以找到一組有特別性質的\(x\)來加速帶入，與轉回多項式?
是否可以找到一組有特別性質的\(x\)來加速帶入，與轉回多項式?
可以!用\(\omega_n^{0\sim n-1}\)(在這裡指的是\(x^n=1\)的\(n\)個解)試試看
\begin{bmatrix}
\omega^{0 \cdot 0} & \omega^{0 \cdot 1} & \omega^{0 \cdot 2} & \omega^{0 \cdot 3} & \omega^{0 \cdot 4} & \omega^{0 \cdot 5} & \omega^{0 \cdot 6} & \omega^{0 \cdot 7} \\
\omega^{1 \cdot 0} & \omega^{1 \cdot 1} & \omega^{1 \cdot 2} & \omega^{1 \cdot 3} & \omega^{1 \cdot 4} & \omega^{1 \cdot 5} & \omega^{1 \cdot 6} & \omega^{1 \cdot 7} \\
\omega^{2 \cdot 0} & \omega^{2 \cdot 1} & \omega^{2 \cdot 2} & \omega^{2 \cdot 3} & \omega^{2 \cdot 4} & \omega^{2 \cdot 5} & \omega^{2 \cdot 6} & \omega^{2 \cdot 7} \\
\omega^{3 \cdot 0} & \omega^{3 \cdot 1} & \omega^{3 \cdot 2} & \omega^{3 \cdot 3} & \omega^{3 \cdot 4} & \omega^{3 \cdot 5} & \omega^{3 \cdot 6} & \omega^{3 \cdot 7} \\
\omega^{4 \cdot 0} & \omega^{4 \cdot 1} & \omega^{4 \cdot 2} & \omega^{4 \cdot 3} & \omega^{4 \cdot 4} & \omega^{4 \cdot 5} & \omega^{4 \cdot 6} & \omega^{4 \cdot 7} \\
\omega^{5 \cdot 0} & \omega^{5 \cdot 1} & \omega^{5 \cdot 2} & \omega^{5 \cdot 3} & \omega^{5 \cdot 4} & \omega^{5 \cdot 5} & \omega^{5 \cdot 6} & \omega^{5 \cdot 7} \\
\omega^{6 \cdot 0} & \omega^{6 \cdot 1} & \omega^{6 \cdot 2} & \omega^{6 \cdot 3} & \omega^{6 \cdot 4} & \omega^{6 \cdot 5} & \omega^{6 \cdot 6} & \omega^{6 \cdot 7} \\
\omega^{7 \cdot 0} & \omega^{7 \cdot 1} & \omega^{7 \cdot 2} & \omega^{7 \cdot 3} & \omega^{7 \cdot 4} & \omega^{7 \cdot 5} & \omega^{7 \cdot 6} & \omega^{7 \cdot 7} \\
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_1\\
a_2\\
a_3\\
a_4\\
a_5\\
a_6\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
這裡用\(\omega\)代替\(\omega_8\)
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{1} & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{3} & \omega^{6} & \omega^{1} & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega^{1} & \omega^{6} & \omega^{3} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} \\
\omega^{0} & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega^{1}
\end{bmatrix}
這裡用\(\omega\)代替\(\omega_8\)
\begin{bmatrix}
a_0\\
a_1\\
a_2\\
a_3\\
a_4\\
a_5\\
a_6\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{1} & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{3} & \omega^{6} & \omega^{1} & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega^{1} & \omega^{6} & \omega^{3} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} \\
\omega^{0} & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega^{1}
\end{bmatrix}
先把奇偶拆開來
\begin{bmatrix}
a_0\\
a_1\\
a_2\\
a_3\\
a_4\\
a_5\\
a_6\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
先把奇偶拆開來
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
第\(i(i<\frac{n}{2})\) row的偶數項和第\(i+\frac{n}{2}\)row 一模一樣!
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
神奇的事出現了!
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
第\(i(i<4\) row的奇數項和第\(i+4\) row 差\(\omega^{4}\)!
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{3} & \omega^{1} & \omega^{7} & \omega^{5} \\
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6\\
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
試圖由上半得到下半
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3\\
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
試圖由上半得到下半
切切切!
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
+
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{3} & \omega^{1} & \omega^{7} & \omega^{5}
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
+
\begin{bmatrix}
\omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3
\end{bmatrix}
試圖由上半得到下半
切切切!
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
+
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{3} & \omega^{1} & \omega^{7} & \omega^{5}
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
+
\begin{bmatrix}
\omega^{4} & \omega^{4} & \omega^{4} & \omega^{4} \\
\omega^{5} & \omega^{7} & \omega^{1} & \omega^{3} \\
\omega^{6} & \omega^{2} & \omega^{6} & \omega^{2} \\
\omega^{7} & \omega^{5} & \omega^{3} & \omega^{1}
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3
\end{bmatrix}
上下一模一樣!
上下差\(\omega^4\)!
試圖由上半得到下半
切切切!
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
+
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{3} & \omega^{1} & \omega^{7} & \omega^{5}
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
+\omega^{4}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{3} & \omega^{1} & \omega^{7} & \omega^{5}
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3
\end{bmatrix}
試圖由上半得到下半
切切切!
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
+
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{3} & \omega^{1} & \omega^{7} & \omega^{5}
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
-
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{3} & \omega^{1} & \omega^{7} & \omega^{5}
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
=
\begin{bmatrix}
y_4\\
y_5\\
y_6\\
y_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
=
\begin{bmatrix}
y_0\\
y_1\\
y_2\\
y_3
\end{bmatrix}
好像快會了喔
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{1} & \omega^{3} & \omega^{5} & \omega^{7} \\
\omega^{2} & \omega^{6} & \omega^{2} & \omega^{6} \\
\omega^{3} & \omega^{1} & \omega^{7} & \omega^{5}
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
和
只要求出
就好了
好像快會了喔
\begin{bmatrix}
\omega^{0+0} & \omega^{0+0} & \omega^{0+4} & \omega^{0+6} \\
\omega^{1+0} & \omega^{1+2} & \omega^{1+4} & \omega^{1+6} \\
\omega^{2+0} & \omega^{2+4} & \omega^{2+0} & \omega^{2+4} \\
\omega^{3+0} & \omega^{3+6} & \omega^{3+4} & \omega^{3+2}
\end{bmatrix}
\begin{bmatrix}
a_1\\
a_3\\
a_5\\
a_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
和
只要求出
就好了
再提出一次\(\omega\)
好像快會了喔
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
\begin{bmatrix}
\ 1/\omega^0\ a_1\\
\ 1/\omega^1\ a_3\\
\ 1/\omega^2\ a_5\\
\ 1/\omega^3\ a_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
和
只要求出
就好了
因為\(\omega_{n}^{i} = \omega_{\frac{n}{2}}^{\frac{i}{2}}\)，
會發現其實上述兩坨東西都是再做一次大小砍半的事(DFT)
好像快會了喔
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
\begin{bmatrix}
\ 1/\omega^0\ a_1\\
\ 1/\omega^1\ a_3\\
\ 1/\omega^2\ a_5\\
\ 1/\omega^3\ a_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
和
只要求出
就好了
因為\(\omega_{n}^{i} = \omega_{\frac{n}{2}}^{\frac{i}{2}}\)，
會發現其實上述兩坨東西都是再做一次大小砍半的事(DFT)
分治!
根據主定理，總時間複雜度\(O(n \log n)\)
好像快會了喔
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
\begin{bmatrix}
\ 1/\omega^0\ a_1\\
\ 1/\omega^1\ a_3\\
\ 1/\omega^2\ a_5\\
\ 1/\omega^3\ a_7
\end{bmatrix}
\begin{bmatrix}
a_0\\
a_2\\
a_4\\
a_6
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0}\\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6}\\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4}\\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2}
\end{bmatrix}
和
只要求出
就好了
參考code
//CD為complex<double>
void FFT (vector <CD>& a) {
int n = a.size();
if (n == 1) return;
vector <CD> even(n / 2), odd(n / 2);
for (int i = 0; i < n / 2; i++) even[i] = a[i * 2], odd[i] = a[i * 2 + 1];
FFT(even, inv); FFT(odd, inv);
for (int i = 0; i < n / 2; i++) {
CD z = OMEGA(i, n);
a[i] = even[i] + odd[i] * z;
a[i + n / 2] = even[i] - odd[i] * z;
}
return;}我們現在會很快地得到多項式圖形上的\(n\)個點了!
那要怎麼很快從多個點轉回多項式?
我們現在會很快地得到多項式圖形上的\(n\)個點了!
那要怎麼很快從多個點轉回多項式?
我們剛剛帶入點是用矩陣乘法對吧，也就是\(TA\)=\(Y_A\)
然後我們會用\(Y_A,Y_B\)得到\(Y_C\)
要怎麼從\(Y_C\)得到\(C\)?
我們現在會很快地得到多項式圖形上的\(n\)個點了!
那要怎麼很快從多個點轉回多項式?
我們剛剛帶入點是用矩陣乘法對吧，也就是\(TA\)=\(Y_A\)
然後我們會用\(Y_A,Y_B\)得到\(Y_C\)
要怎麼從\(Y_C\)得到\(C\)?
再乘一個\(T^{-1}\)! 它是誰呢?
我們現在會很快地得到多項式圖形上的\(n\)個點了!
那要怎麼很快從多個點轉回多項式?
我們剛剛帶入點是用矩陣乘法對吧，也就是\(TA\)=\(Y_A\)
然後我們會用\(Y_A,Y_B\)得到\(Y_C\)
要怎麼從\(Y_C\)得到\(C\)?
再乘一個\(T^{-1}\)! 它是誰呢?
通靈一下，跳結論考慮一下\(T\=T\)，這裡的\(\=T\)指的是對T的每個元素取共軛
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{-1} & \omega^{-2} & \omega^{-3} & \omega^{-4} & \omega^{-5} & \omega^{-6} & \omega^{-7} \\
\omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} & \omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} \\
\omega^{0} & \omega^{-3} & \omega^{-6} & \omega^{-1} & \omega^{-4} & \omega^{-7} & \omega^{-2} & \omega^{-5} \\
\omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} \\
\omega^{0} & \omega^{-5} & \omega^{-2} & \omega^{-7} & \omega^{-4} & \omega^{-1} & \omega^{-6} & \omega^{-3} \\
\omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} & \omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} \\
\omega^{0} & \omega^{-7} & \omega^{-6} & \omega^{-5} & \omega^{-4} & \omega^{-3} & \omega^{-2} & \omega^{-1}
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{1} & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{3} & \omega^{6} & \omega^{1} & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega^{1} & \omega^{6} & \omega^{3} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} \\
\omega^{0} & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega^{1}
\end{bmatrix}
考慮一下\(T\=T\)，這裡的\(\=T\)指的是對T的每個元素取共軛
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{-1} & \omega^{-2} & \omega^{-3} & \omega^{-4} & \omega^{-5} & \omega^{-6} & \omega^{-7} \\
\omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} & \omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} \\
\omega^{0} & \omega^{-3} & \omega^{-6} & \omega^{-1} & \omega^{-4} & \omega^{-7} & \omega^{-2} & \omega^{-5} \\
\omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} \\
\omega^{0} & \omega^{-5} & \omega^{-2} & \omega^{-7} & \omega^{-4} & \omega^{-1} & \omega^{-6} & \omega^{-3} \\
\omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} & \omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} \\
\omega^{0} & \omega^{-7} & \omega^{-6} & \omega^{-5} & \omega^{-4} & \omega^{-3} & \omega^{-2} & \omega^{-1}
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{1} & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{3} & \omega^{6} & \omega^{1} & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega^{1} & \omega^{6} & \omega^{3} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} \\
\omega^{0} & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega^{1}
\end{bmatrix}
發現第\(i\) row和第\(i\) column其實一樣，取負號乘起來就會變\(n\)個\(\omega^0\)
考慮一下\(T\=T\)，這裡的\(\=T\)指的是對T的每個元素取共軛
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{-1} & \omega^{-2} & \omega^{-3} & \omega^{-4} & \omega^{-5} & \omega^{-6} & \omega^{-7} \\
\omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} & \omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} \\
\omega^{0} & \omega^{-3} & \omega^{-6} & \omega^{-1} & \omega^{-4} & \omega^{-7} & \omega^{-2} & \omega^{-5} \\
\omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} \\
\omega^{0} & \omega^{-5} & \omega^{-2} & \omega^{-7} & \omega^{-4} & \omega^{-1} & \omega^{-6} & \omega^{-3} \\
\omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} & \omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} \\
\omega^{0} & \omega^{-7} & \omega^{-6} & \omega^{-5} & \omega^{-4} & \omega^{-3} & \omega^{-2} & \omega^{-1}
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{1} & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{3} & \omega^{6} & \omega^{1} & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega^{1} & \omega^{6} & \omega^{3} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} \\
\omega^{0} & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega^{1}
\end{bmatrix}
發現第\(i\) row和第\(i\) column其實一樣，取負號乘起來就會變\(n\)個\(\omega^0\)
=
\begin{bmatrix}
n\omega^{0} & & & & & & & \\
& n\omega^{0} & & & & & & \\
& & n\omega^{0} & & & & & \\
& & & n\omega^{0} & & & & \\
& & & & n\omega^{0} & & & \\
& & & & & n\omega^{0} & & \\
& & & & & & n\omega^{0} & \\
& & & & & & & n\omega^{0}
\end{bmatrix}
考慮一下\(T\=T\)，這裡的\(\=T\)指的是對T的每個元素取共軛
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{-1} & \omega^{-2} & \omega^{-3} & \omega^{-4} & \omega^{-5} & \omega^{-6} & \omega^{-7} \\
\omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} & \omega^{0} & \omega^{-2} & \omega^{-4} & \omega^{-6} \\
\omega^{0} & \omega^{-3} & \omega^{-6} & \omega^{-1} & \omega^{-4} & \omega^{-7} & \omega^{-2} & \omega^{-5} \\
\omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} & \omega^{0} & \omega^{-4} \\
\omega^{0} & \omega^{-5} & \omega^{-2} & \omega^{-7} & \omega^{-4} & \omega^{-1} & \omega^{-6} & \omega^{-3} \\
\omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} & \omega^{0} & \omega^{-6} & \omega^{-4} & \omega^{-2} \\
\omega^{0} & \omega^{-7} & \omega^{-6} & \omega^{-5} & \omega^{-4} & \omega^{-3} & \omega^{-2} & \omega^{-1}
\end{bmatrix}
\begin{bmatrix}
\omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} & \omega^{0} \\
\omega^{0} & \omega^{1} & \omega^{2} & \omega^{3} & \omega^{4} & \omega^{5} & \omega^{6} & \omega^{7} \\
\omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} & \omega^{0} & \omega^{2} & \omega^{4} & \omega^{6} \\
\omega^{0} & \omega^{3} & \omega^{6} & \omega^{1} & \omega^{4} & \omega^{7} & \omega^{2} & \omega^{5} \\
\omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} & \omega^{0} & \omega^{4} \\
\omega^{0} & \omega^{5} & \omega^{2} & \omega^{7} & \omega^{4} & \omega^{1} & \omega^{6} & \omega^{3} \\
\omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} & \omega^{0} & \omega^{6} & \omega^{4} & \omega^{2} \\
\omega^{0} & \omega^{7} & \omega^{6} & \omega^{5} & \omega^{4} & \omega^{3} & \omega^{2} & \omega^{1}
\end{bmatrix}
=
\begin{bmatrix}
n\omega^{0} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & n\omega^{0} & 0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & n\omega^{0} & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & n\omega^{0} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & n\omega^{0} & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & n\omega^{0} & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & n\omega^{0} & 0 \\
0 & 0 & 0 & 0 & 0 & 0 & 0 & n\omega^{0}
\end{bmatrix}
被嗆說這就是角速度
每一圈加總都是0，也就是說全都是0
每一圈加總都是0，也就
\(T\=T=nI_n\)
\(T^{-1}\)其實就是\(\frac{1}{n}\=T\)
瑣事-DFT
- 剛剛把\(\omega\)帶入方程式的動作稱為DFT
- 把點變回方程式叫做IDFT
- 一次FFT由兩次DFT、一次IDFT組成，\(O(n\log n)\)
瑣事-實作
- 資料型態為complex<double>，內建四則運算
- 先把所有的\(\omega_N\)找出來很好，這個\(N\)是多項式\(C\)的次數
完整code
using ld = long double;
using CD = complex<ld>;
CD OMEGA (int i, int n) {
ld angle = i;
angle = angle / n * (2 * pi);
return CD(cos(angle), sin(angle));
}
void FFT (vector <CD>& a, bool inv = 0) {
int n = a.size();
if (n == 1) return;
vector <CD> even(n / 2), odd(n / 2);
for (int i = 0; i < n / 2; i++) even[i] = a[i * 2], odd[i] = a[i * 2 + 1];
FFT(even, inv); FFT(odd, inv);
for (int i = 0; i < n / 2; i++) {
CD z = OMEGA(i * (inv?-1:1), n);
a[i] = even[i] + odd[i] * z;
a[i + n / 2] = even[i] - odd[i] * z;
if (inv) a[i] /= 2, a[i + n / 2] /= 2;
}
return;}NTT
為什麼FFT是好的?
為什麼FFT是好的?
因為\((\omega_n^{i})^{2j}=(\omega_n^{i+\frac{n}{2}})^{2j}\)和\(-(\omega_n^{i})^{2j+1}=(\omega_n^{i+\frac{n}{2}})^{2j+1}\)
為什麼FFT是好的?
因為\((\omega_n^{i})^{2j}=(\omega_n^{i+\frac{n}{2}})^{2j}\)和\(-(\omega_n^{i})^{2j+1}=(\omega_n^{i+\frac{n}{2}})^{2j+1}\)
什麼也有這個性質?(可以拿來取代單位根)
還記得野獸先備裡面有甚麼嗎?
為什麼FFT是好的?
因為\((\omega_n^{i})^{2j}=(\omega_n^{i+\frac{n}{2}})^{2j}\)和\(-(\omega_n^{i})^{2j+1}=(\omega_n^{i+\frac{n}{2}})^{2j+1}\)
什麼也有這個性質?(可以拿來取代單位根)
還記得野獸先備裡面有甚麼嗎?
在模質數\(M=r\times 2^k+1\)之下為\(M\)的原根\(g\)的\(r\)次方
為什麼FFT是好的?
因為\((\omega_n^{i})^{2j}=(\omega_n^{i+\frac{n}{2}})^{2j}\)和\(-(\omega_n^{i})^{2j+1}=(\omega_n^{i+\frac{n}{2}})^{2j+1}\)
什麼也有這個性質?(可以拿來取代單位根)
還記得野獸先備裡面有甚麼嗎?
在模質數\(M=r\times 2^k+1\)之下為\(M\)的原根\(g\)的\(r\)次方
\((g^r)^{n}=g^{r\times 2^k}\)\(=g^{M-1}\equiv1\)
為什麼FFT是好的?
因為\((\omega_n^{i})^{2j}=(\omega_n^{i+\frac{n}{2}})^{2j}\)和\(-(\omega_n^{i})^{2j+1}=(\omega_n^{i+\frac{n}{2}})^{2j+1}\)
什麼也有這個性質?(可以拿來取代單位根)
還記得野獸先備裡面有甚麼嗎?
在模質數\(M=r\times 2^k+1\)之下為\(M\)的原根\(g\)的\(r\)次方
\((g^r)^{n}=g^{r\times 2^k}\)\(=g^{M-1}\equiv 1\)
\((g^r)^{\frac{n}{2}}=g^{r\times 2^{k-1}}\)\(=g^\frac{M-1}{2}\equiv \pm1\)(正不合因為還沒繞一圈)
參考code
using ll = long long;
const int M = 998244353;
void NTT (vector <ll>& a, bool inv = 0) {
int n = a.size();
if (n == 1) return;
vector <ll> even(n / 2), odd(n / 2);
for (int i = 0; i < n / 2; i++) even[i] = a[i * 2], odd[i] = a[i * 2 + 1];
NTT(even, inv);
NTT(odd, inv);
for (int i = 0; i < n / 2; i++) {
ll z = OMEGA(i, n);
a[i] = (even[i] + odd[i] * z) % M;
a[i + n / 2] = (even[i] - odd[i] * z) % M;
a[i] = (a[i] % M + M) % M;
a[i + n / 2] = (a[i + n / 2] % M + M) % M;
}
if (inv and n == nn) {
int qq = f(n, M-2);
for (int i = 0; i < n; i++){
a[i] *= qq;
a[i] = (a[i] % M + M) % M;
}
}
return;}
...
...
...
omega[0] = 1, omega[1] = f(3, (M - 1) / nn);
for (int i = 2; i <= nn; i++) omega[i] = omega[i - 1] * omega[1] % M;常用模數
- \(998244353=119\times2^{23}+1\)，\(g=3\)
- \(1004535809=479\times2^{21}+1\)，\(g=3\)
- \(469762049=7\times2^{26}+1\)，\(g=3\)
- 可以上網看一下NTT常用模數表
- 原根不一定只有一個，但只要背一個就好
FFT v.s. NTT
- FFT需要浮點數，精度可能燒雞
- NTT的值雖然是整數，但全都模過\(M\)
- 運行上，NTT會快一點
丟掉遞迴
丟掉手錶丟外套丟掉背包再丟嘮叨丟掉電視丟電腦丟掉大腦再丟煩惱衝啥大衝啥小\(a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7\)
\(a_1, a_3, a_5, a_7\)
\(a_0, a_4\)
\(a_0, a_2, a_4, a_6\)
\(a_2, a_6\)
\(a_1, a_5\)
\(a_3, a_7\)
\(a_0\)
\(a_4\)
\(a_2\)
\(a_6\)
\(a_1\)
\(a_5\)
\(a_3\)
\(a_7\)
DFT架構圖
\(a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7\)
\(a_1, a_3, a_5, a_7\)
\(a_0, a_4\)
\(a_0, a_2, a_4, a_6\)
\(a_2, a_6\)
\(a_1, a_5\)
\(a_3, a_7\)
\(a_0\)
\(a_4\)
\(a_2\)
\(a_6\)
\(a_1\)
\(a_5\)
\(a_3\)
\(a_7\)
顯然可以排序成最下面那排，再一一往上合併
\(a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7\)
\(a_1, a_3, a_5, a_7\)
\(a_0, a_4\)
\(a_0, a_2, a_4, a_6\)
\(a_2, a_6\)
\(a_1, a_5\)
\(a_3, a_7\)
\(a_0\)
\(a_4\)
\(a_2\)
\(a_6\)
\(a_1\)
\(a_5\)
\(a_3\)
\(a_7\)
000
100
010
110
001
101
011
111
二進位
\(a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7\)
\(a_1, a_3, a_5, a_7\)
\(a_0, a_4\)
\(a_0, a_2, a_4, a_6\)
\(a_2, a_6\)
\(a_1, a_5\)
\(a_3, a_7\)
\(a_0\)
\(a_4\)
\(a_2\)
\(a_6\)
\(a_1\)
\(a_5\)
\(a_3\)
\(a_7\)
000
100
010
110
001
101
011
111
二進位
反二進位
000
001
010
011
100
101
110
111
其實是對reverse的二進位排序!
\(a_0, a_1, a_2, a_3, a_4, a_5, a_6, a_7\)
\(a_1, a_3, a_5, a_7\)
\(a_0, a_4\)
\(a_0, a_2, a_4, a_6\)
\(a_2, a_6\)
\(a_1, a_5\)
\(a_3, a_7\)
\(a_0\)
\(a_4\)
\(a_2\)
\(a_6\)
\(a_1\)
\(a_5\)
\(a_3\)
\(a_7\)
其實是對reverse的二進位排序!
對最後一位排序
對第二位排序
對首位排序
參考code
using ll = long long;
const int M = 998244353;
int rev[2010000];
ll omega[2010000];
void NTT (vector <ll>& a) {
//排序
int n = a.size();
int k = __lg(n);
memset(rev, 0, sizeof(rev));
for (int i = 0; i < nn; i++) for (int j = 0; j < k; j++)
rev[i] += (1 << j) * ((i >> (k - 1 - j)) & 1);
for (int i = 0; i < nn; i++) if (rev[i] < i) swap(a[i], a[rev[i]]);
//NTT，我這裡是用滾動的
vector <ll> ans[2] = {a, a};
int lst = 0, now = 1;
for (int len = 2; len <= nn; len *= 2) {
for (int j = 0; j < nn; j += len) {
for (int p = j; p < j + len / 2; p++) {
ll c = ans[lst][p], d = ans[lst][p + len / 2];
ans[now][p] = ((c + OMEGA(p - j, len) * d) % M + M) % M;
ans[now][p + len / 2] = ((c + OMEGA(p - j + len / 2, len) * d) % M + M) % M;
}
}
swap(lst, now);
}
a = ans[lst];
return;}優點
- 跑比較快
任意模數FFT
與其說是任意模數不如說是求得真值後，
再對一個任意的模數取模
3NTT
- 做三次NTT
- 中國剩餘定理
- 聰明的合併、取模或大數處理
3NTT
- 做三次NTT
- 中國剩餘定理
- 聰明的合併、取模或大數處理
- 不會中國剩餘定理的請舉手
3NTT
- 做三次NTT
- 中國剩餘定理
- 聰明的合併、取模或大數處理
- 不會中國剩餘定理的請舉手
- 記得學一下
，你們現在可能不知道，但我下次看到你們的時候，你們就知道為什麼很重要了(by蔡孟宗)
3NTT 參考code
MTT
- 神仙FFT
- 把一個多項式拆成兩個來減少精度造成的影響
- 純樸做要12次DFT，但可以優化到4次
FWHT(一般化位元卷積)
FFT 是想要快速算出$$c_k=\sum_{i+j=k}a_i\ b_j$$
FWHT 是想要快速算出$$c_k=\sum_{f(i,j)=k}a_i\ b_j$$
這個\(f(i,j)\)可以是任何二元位元運算
同樣的方法甚至可以擴展到某些不是位元運算的運算
我們先直接接受FWHT和FFT可以用一樣的方法做
- 算\(TA\), \(TB\)
- 用\(TA\), \(TB\)做出\(TC\)
- 算\(T^{-1}TC\)，得到\(C\)
以XOR為例
\(F\)是誰?
以XOR為例子
先看2*2的矩陣\(T_2=\begin{bmatrix}w&x\\y&z\end{bmatrix}\)
我們要\(T_2\begin{bmatrix}a_0\\a_1\end{bmatrix}\cdot\) \(T_2\begin{bmatrix}b_0\\b_1\end{bmatrix}=\) \(T_2\begin{bmatrix}c_0\\c_1\end{bmatrix}=\) \(T_2\begin{bmatrix}a_0b_0+a_1b_1\\a_0b_1+a_1b_0\end{bmatrix}\)
內積(點積)
以XOR為例子
先看2*2的矩陣\(T_2=\begin{bmatrix}w&x\\y&z\end{bmatrix}\)
我們要\(T_2\begin{bmatrix}a_0\\a_1\end{bmatrix}\cdot\) \(T_2\begin{bmatrix}b_0\\b_1\end{bmatrix}=\) \(T_2\begin{bmatrix}c_0\\c_1\end{bmatrix}=\) \(T_2\begin{bmatrix}a_0b_0+a_1b_1\\a_0b_1+a_1b_0\end{bmatrix}\)
\begin{bmatrix}
wa_0+xa_1\\
ya_0+za_1
\end{bmatrix}
\cdot
\begin{bmatrix}
wb_0+xb_1\\
yb_0+zb_1
\end{bmatrix}
=
\begin{bmatrix}
w(a_0b_0+a_1b_1)+x(a_0b_1+a_1b_0)\\
y(a_0b_0+a_1b_1)+z(a_0b_1+a_1b_0)
\end{bmatrix}
以XOR為例子
先看2*2的矩陣\(T_2=\begin{bmatrix}w&x\\y&z\end{bmatrix}\)
我們要\(T_2\begin{bmatrix}a_0\\a_1\end{bmatrix}\cdot\) \(T_2\begin{bmatrix}b_0\\b_1\end{bmatrix}=\) \(T_2\begin{bmatrix}c_0\\c_1\end{bmatrix}=\) \(T_2\begin{bmatrix}a_0b_0+a_1b_1\\a_0b_1+a_1b_0\end{bmatrix}\)
\begin{bmatrix}
w^2a_0b_0 + wxa_0b_1 + wxa_1b_0 + x^2a_1b_1\\
y^2a_0b_0 + yza_0b_1 + yza_1b_0 + z^2a_1b_1
\end{bmatrix}
=
\begin{bmatrix}
wa_0b_0+xa_0b_1+xa_1b_0+xa_1b_1\\
ya_0b_0+za_0b_1+ya_1b_0+za_1b_1
\end{bmatrix}
以XOR為例子
先看2*2的矩陣\(T_2=\begin{bmatrix}w&x\\y&z\end{bmatrix}\)
我們要\(T_2\begin{bmatrix}a_0\\a_1\end{bmatrix}\cdot\) \(T_2\begin{bmatrix}b_0\\b_1\end{bmatrix}=\) \(T_2\begin{bmatrix}c_0\\c_1\end{bmatrix}=\) \(T_2\begin{bmatrix}a_0b_0+a_1b_1\\a_0b_1+a_1b_0\end{bmatrix}\)
\begin{bmatrix}
w^2a_0b_0 + wxa_0b_1 + wxa_1b_0 + x^2a_1b_1\\
y^2a_0b_0 + yza_0b_1 + yza_1b_0 + z^2a_1b_1
\end{bmatrix}
=
\begin{bmatrix}
wa_0b_0+xa_0b_1+xa_1b_0+xa_1b_1\\
ya_0b_0+za_0b_1+ya_1b_0+za_1b_1
\end{bmatrix}
\begin{cases}
w^2=w\\
wx=x\\
x^2=w
\end{cases}
\begin{cases}
y^2=y\\
yz=z\\
z^2=y
\end{cases}
得到方程組
以XOR為例子
先看2*2的矩陣\(T_2=\begin{bmatrix}w&x\\y&z\end{bmatrix}\)
我們要\(T_2\begin{bmatrix}a_0\\a_1\end{bmatrix}\cdot\) \(T_2\begin{bmatrix}b_0\\b_1\end{bmatrix}=\) \(T_2\begin{bmatrix}c_0\\c_1\end{bmatrix}=\) \(T_2\begin{bmatrix}a_0b_0+a_1b_1\\a_0b_1+a_1b_0\end{bmatrix}\)
\begin{bmatrix}
w^2a_0b_0 + wxa_0b_1 + wxa_1b_0 + x^2a_1b_1\\
y^2a_0b_0 + yza_0b_1 + yza_1b_0 + z^2a_1b_1
\end{bmatrix}
=
\begin{bmatrix}
wa_0b_0+xa_0b_1+xa_1b_0+xa_1b_1\\
ya_0b_0+za_0b_1+ya_1b_0+za_1b_1
\end{bmatrix}
\((w,x)\)和\((y,z)\)皆可為\((0,0),(1,1),(1,-1)\)
以XOR為例子
先看2*2的矩陣\(T_2=\begin{bmatrix}w&x\\y&z\end{bmatrix}\)
我們要\(T_2\begin{bmatrix}a_0\\a_1\end{bmatrix}\cdot\) \(T_2\begin{bmatrix}b_0\\b_1\end{bmatrix}=\) \(T_2\begin{bmatrix}c_0\\c_1\end{bmatrix}=\) \(T_2\begin{bmatrix}a_0b_0+a_1b_1\\a_0b_1+a_1b_0\end{bmatrix}\)
\begin{bmatrix}
w^2a_0b_0 + wxa_0b_1 + wxa_1b_0 + x^2a_1b_1\\
y^2a_0b_0 + yza_0b_1 + yza_1b_0 + z^2a_1b_1
\end{bmatrix}
=
\begin{bmatrix}
wa_0b_0+xa_0b_1+xa_1b_0+xa_1b_1\\
ya_0b_0+za_0b_1+ya_1b_0+za_1b_1
\end{bmatrix}
\((w,x)\)和\((y,z)\)皆可為\((0,0),(1,1),(1,-1)\)
因為\(T_2\)可逆，所以\(T_2=\begin{bmatrix}1&1\\1&-1\end{bmatrix}\)，發現\(T_2^{-1}=\frac{1}{2}T_2\)
以XOR為例子-將\(T_2\)擴展
\(T_2=\begin{bmatrix}1&1\\1&-1\end{bmatrix}\)
將多項式\(A\)(長度為4)分成兩半\(A_0\),\(A_1\)，個別視作單一元素
我們要\(U\begin{bmatrix}T_2 A_0\\T_2 A_1\end{bmatrix}\cdot\) \(U\begin{bmatrix}T_2 B_0\\T_2 B_1\end{bmatrix}=\) \(U\begin{bmatrix}T_2 C_0\\T_2 C_1\end{bmatrix}=\) \(U\begin{bmatrix}T_2A_0B_0+T_2A_1B_1\\T_2A_0B_1+T_2A_1B_0\end{bmatrix}\)
以XOR為例子-將\(T_2\)擴展
\(T_2=\begin{bmatrix}1&1\\1&-1\end{bmatrix}\)
將多項式\(A\)(長度為4)分成兩半\(A_0\),\(A_1\)，個別視作單一元素
我們要\(U\begin{bmatrix}T_2 A_0\\T_2 A_1\end{bmatrix}\cdot\) \(U\begin{bmatrix}T_2 B_0\\T_2 B_1\end{bmatrix}=\) \(U\begin{bmatrix}T_2 C_0\\T_2 C_1\end{bmatrix}=\) \(U\begin{bmatrix}T_2A_0B_0+T_2A_1B_1\\T_2A_0B_1+T_2A_1B_0\end{bmatrix}\)
根據之前的經驗可以得到\(U=\begin{bmatrix}I_2&I_2\\I_2&-I_2\end{bmatrix}\)，可以分治做事。
還可以得到滿足\(T_4A\cdot\) \(T_4B=\) \(T_4C\)的\(T_4=\begin{bmatrix}T_2&T_2\\T_2&-T_2\end{bmatrix}\)
以XOR為例子-參考code(700ms)
using ll = long long;
const int M = 998244353;
int k;
vector<ll> FWHT (vector<ll>&a) {
int n = a.size();
if (n == 1) return a;
vector<ll> zero(n / 2), one(n / 2);
for (int i = 0; i < n / 2; i++) zero[i] = a[i], one[i] = a[i + n / 2];
zero = FWHT(zero), one = FWHT(one);
for (int i = 0; i < n / 2; i++) a[i] = zero[i] + one[i], a[i + n / 2] = zero[i] - one[i];
for (int i = 0; i < n; i++) a[i] = (a[i] % M + M) % M;
return a;
}
int main () {
cin >> k;
int n = (1 << k);
vector <ll> a(n), b(n), c(n);
for (auto &x : a) cin >> x;
for (auto &x : b) cin >> x;
a = FWHT(a), b = FWHT(b);
for (int i = 0; i < n; i++) c[i] = a[i] * b[i] % M;
c = FWHT(c);
for (int i = 0; i < n; i++) c[i] = c[i] * fmul(n, M - 2) % M;
for (int i = 0; i < n; i++) cout << c[i] << ' ';
cout << '\n';
}以XOR為例子-參考code-迭代(200ms)
vector<ll> FWHT (vector<ll>&a) {
int n = a.size();
if (n == 1) return a;
for (int len = 2; len <= n; len <<= 1) {
int sml = len / 2;
for (int i = 0; i < n / len; i++) {
for (int j = 0; j < sml; j++) {
int old0 = a[i * len + j], old1 = a[i * len + j + sml];
a[i * len + j] = (old0 + old1) % M;
a[i * len + j + sml] = (old0 - old1 + M) % M;
}
}
}
return a;
}OR, AND之類的也可以這樣先列式處理2*2再擴展到更大
OR的矩陣是\(\begin{bmatrix}1&0\\1&1\end{bmatrix}\)
AND的矩陣是\(\begin{bmatrix}0&1\\1&1\end{bmatrix}\)
瑣事-指稱
- 這種位元卷積的一般化解法可以叫做FWHT
- FWHT曾專指XOR卷積
OR卷積和SOS DP
OR卷積的矩陣長得像\(\begin{bmatrix}1&0\\1&1\end{bmatrix}\)
OR卷積的矩陣長得像\(\begin{bmatrix}1&0\\1&1\end{bmatrix}\)
vector<int> FWHT (vector<int>&a) {
int n = a.size();
if (n == 1) return a;
for (int len = 2; len <= n; len <<= 1) {
int sml = len / 2;
for (int i = 0; i < n / len; i++) {
for (int j = 0; j < sml; j++) {
a[i * len + j + sml] = (a[i * len + j] + a[i * len + j + sml]) % M;
}
}
}
return a;
}code可能長的像這樣
OR卷積的矩陣長得像\(\begin{bmatrix}1&0\\1&1\end{bmatrix}\)
vector<int> FWHT (vector<int>&a) {
int n = a.size();
if (n == 1) return a;
for (int len = 2; len <= n; len <<= 1) {
int sml = len / 2;
for (int i = 0; i < n / len; i++) {
for (int j = 0; j < sml; j++) {
a[i * len + j + sml] = (a[i * len + j] + a[i * len + j + sml]) % M;
}
}
}
return a;
}code可能長的像這樣
怎麼有點像SOS ?
OR卷積的矩陣長得像\(\begin{bmatrix}1&0\\1&1\end{bmatrix}\)
vector<int> FWHT (vector<int>&a) {
int n = a.size();
if (n == 1) return a;
for (int len = 2; len <= n; len <<= 1) {
int sml = len / 2;
for (int i = 0; i < n / len; i++) {
for (int j = 0; j < sml; j++) {
a[i * len + j + sml] = (a[i * len + j] + a[i * len + j + sml]) % M;
}
}
}
return a;
}code可能長的像這樣
怎麼有點像SOS ?
因為就真的是SOS
- OR是SOS(子集和)
- AND也是SOS(超集合)
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
\( =\sum_{(i\subseteq k) \land (j\subseteq k)} a_ib_j\)
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
\(=\sum_{(i\subseteq k) \land (j\subseteq k)} a_ib_j\)
\(=(\sum_{i\subseteq k}a_i)(\sum_{j\subseteq k}b_j)\)
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
\(=\sum_{(i\subseteq k) \land (j\subseteq k)} a_ib_j\)
\(=(\sum_{i\subseteq k}a_i)(\sum_{i\subseteq k}b_i)\)
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
\(=\sum_{(i\subseteq k) \land (j\subseteq k)} a_ib_j\)
\(=(\sum_{i\subseteq k}a_i)(\sum_{i\subseteq k}b_i)\) - 怎麼求\((\sum_{i\subseteq k}a_i)\)、\((\sum_{i\subseteq k}b_i)\)?
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
\(=\sum_{(i\subseteq k) \land (j\subseteq k)} a_ib_j\)
\(=(\sum_{i\subseteq k}a_i)(\sum_{i\subseteq k}b_i)\) - 怎麼求\((\sum_{i\subseteq k}a_i)\)、\((\sum_{i\subseteq k}b_i)\)? 子集和
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
\(=\sum_{(i\subseteq k) \land (j\subseteq k)} a_ib_j\)
\(=(\sum_{i\subseteq k}a_i)(\sum_{i\subseteq k}b_i)\) - 怎麼求\((\sum_{i\subseteq k}a_i)\)、\((\sum_{i\subseteq k}b_i)\)? 子集和
- 怎麼把\({c_k}'\)變回\(c_k\)?
- 現在只考慮OR
- \(c_k=\sum_{i\lor j = k}a_i b_j\)
- \({c_k}'=\sum_{(i\lor j)\subseteq k}a_i b_j\)
\(=\sum_{(i\subseteq k) \land (j\subseteq k)} a_ib_j\)
\(=(\sum_{i\subseteq k}a_i)(\sum_{i\subseteq k}b_i)\) - 怎麼求\((\sum_{i\subseteq k}a_i)\)、\((\sum_{i\subseteq k}b_i)\)? 子集和
- 怎麼把\({c_k}'\)變回\(c_k\)? 用子集和的結構來扣
黃色小鴨Pro Max
模板題
如果聽不懂我在講什麼...
-
FFT : -is-this-fft-
-
FWHT : CF blog(看FWHT就好)、leetcode居然也有好文
-
單位根與原根 : 不認識的中國人的網站
-
任意模數 : cnblogs
-
general : ultimate topic list、USACO guide、IOIC 2023
更多令人討厭的...
- 優化
- 多變數 FFT
- CDQ分治FFT
- gcd,lcm卷積
- (max,+)卷積
- 其他奇形怪狀的卷積
- 我其實不知道這是什麼
- 多項式全家桶
- 生成函數
(想學的回家自己卷的)🎉恭喜中国台湾施竣耀同学勇夺IOI金牌
国家栋梁，保送清华、北大
2 0 2 5