KAKURO - A CONSTRAINT SATISFACTION PROBLEM

Özlem Salehi, Adam Glos

Coding Competition

GENERAL SOLUTION

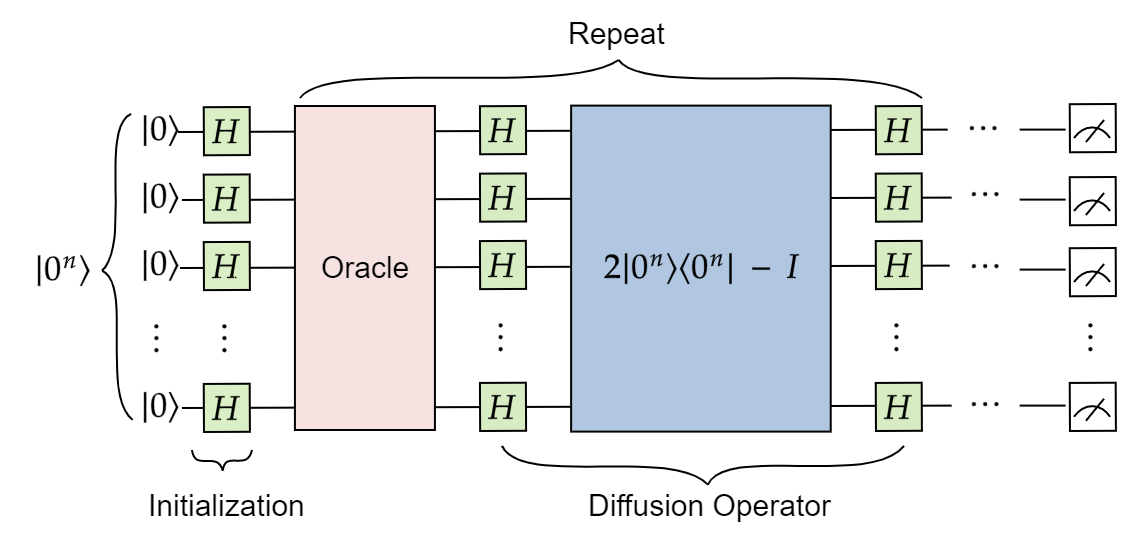
Mark states that correspond to correct assignments

Each binary variable can be represented by a qubit

OUR SOLUTION

Also used in our new paper FUNC-QAOA

Inspiration

GM-QAOA

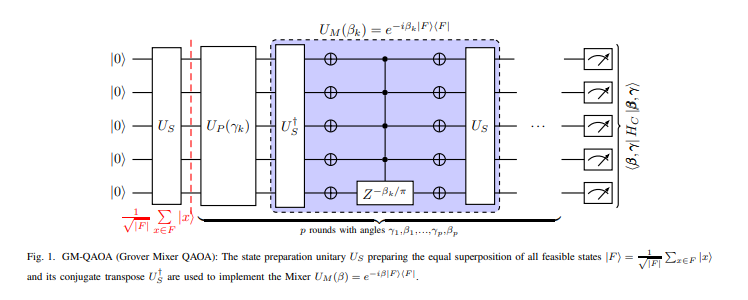
OUR SOLUTION

Some constraints are already handled when preparing the initial state

Custom initial state

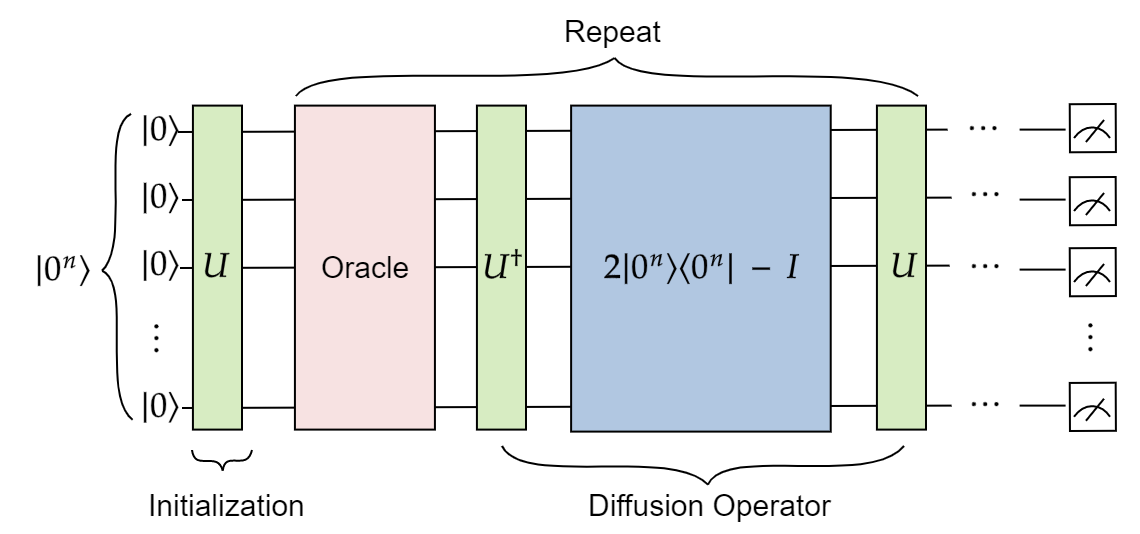
OUR SOLUTION

x_0 \neq x_1\\ x_2+2 \neq x_3\\ x_3 \neq x_4 \\ x_1 \neq x_3\\ x_3 \neq x_5\\ x_5 \neq x_6\\ x_0 \neq x_2\\ x_1 \neq x_5\\ x_4 \neq x_6\\ x_3 = 2\\ x_2+x_4+x_3 = 3

x_0 \neq x_2\\ x_0 \neq x_1\\ x_1 \neq x_5\\ x_5 \neq x_6\\ x_4 \neq x_6\\

x_2+2 \neq x_3\\ x_3 \neq x_4 \\ x_1 \neq x_3\\ x_3 \neq x_5\\ x_3 = 2\\ x_2+x_4+x_3 = 3

= \left(\frac{1}{\sqrt 2}(|101010\rangle + |010101\rangle \right) \otimes \frac{1}{2}\left(|00\rangle + |01\rangle + |10\rangle + |11\rangle \right)

|x_2,x_0,x_1,x_5,x_6,x_4\rangle \otimes |x_3\rangle \\

Initial State

Oracle

Each constraint is checked and information is stored

1: Constraint is satisfied
0: Constraint is not satisfied

MCZ gate is applied on all qubits that hold information about whether the constraint is satisfied

More costly initial state and diffusion operator

DISADVANTAGES

Smaller number of Grover iterations
Simpler oracle resulting in reduced CNOT count

ADVANTAGES

MCZ is implemented with RCCX gates
Some constraints are implemented in place

ADDITIONAL SAVINGS

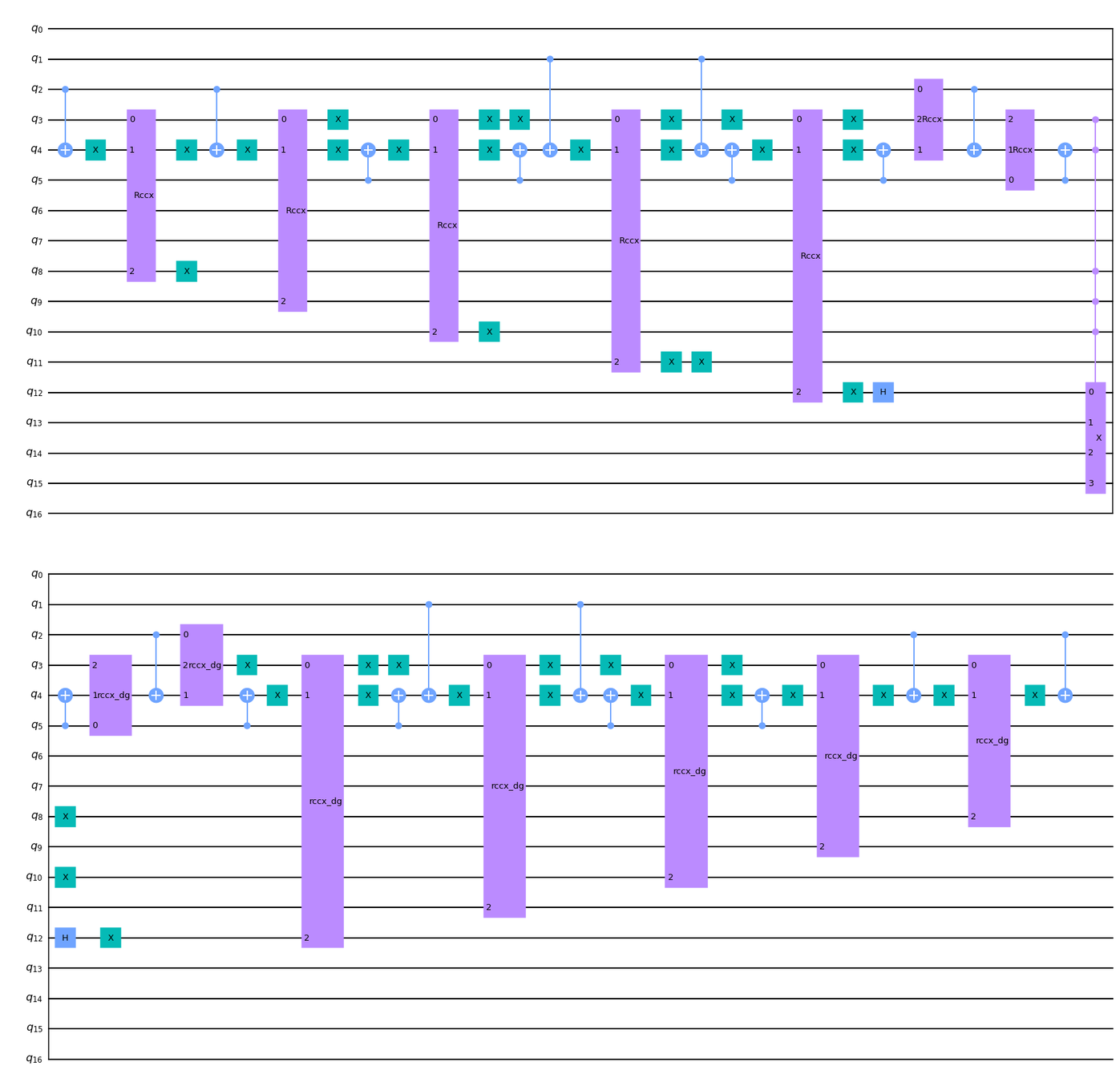
RESULT

86 CNOT gates

Problem

Two cells on the same row/column cannot have the same number.

The sum of the cells on each row/column should equal the matching filled cell.

x_0 \neq x_1\\ x_2+2 \neq x_3\\ x_3 \neq x_4 \\ x_1 \neq x_3\\ x_3 \neq x_5\\ x_5 \neq x_6\\ x_0 \neq x_2\\ x_1 \neq x_5\\ x_4 \neq x_6\\ x_3 = 2\\ x_2+x_4+x_3 = 3

x_i\in \{0,1\}, x_{3} \in \{0,1,2,3\}