Bence Bakó, Adam Glos, Özlem Salehi, Zoltán Zimborás


Near-optimal circuit design for variational quantum optimization

Problem is encoded into the Ising model
$$H_c(s) = -\sum_{i,j}J_{ij}s_is_j - \sum_i h_i s_i$$
Follows the adiabatic evolution defined through time-dependent Hamiltonian
\(H(t) =\frac{1-t}{\tau} \:H_{\rm mix} + \frac{t}{\tau}\: H_c\)
Quantum Annealing

Slow evolution during time \(\tau\)
Implemented by D-Wave quantum annealers
For the gate based model
$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+^n\rangle $$
\(\gamma_i\) and \(\beta_i\) optimized by external classical procedure
Quantum Approximate Optimization Algorithm

Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.
Can be viewed as a trotterization of AQC
Get the corresponding Ising model
\(H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)\)
\(s_i \in \{-1,1\}\)

\(b_i \leftarrow \frac{1-s_i}{2}\)
Implementing QAOA
Start with a
QUBO or HOBO
\(H = -\prod_{i=1}^n b_i\)
\(b_i \in \{0,1\}\)
Exponential number of CNOT gates!
Exponential number of terms !
Get the corresponding Ising model
\(H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)\)
\(s_i \in \{-1,1\}\)
\(b_i \leftarrow \frac{1-s_i}{2}\)
Start with a
QUBO or HOBO
\(H = -\prod_{i=1}^n b_i\)
\(b_i \in \{0,1\}\)
Can we do something else?
Implementing QAOA


\(O(n^2)\) gates on LNN!
FUNC-QAOA
This is classical AND operator!
\(H = -\prod_{i=1}^n b_i\)
\(b_i \in \{0,1\}\)
New Idea
Start with a pseudocode function!
\(|f\rangle \leftarrow AND(b_i\) for \(i=1\) to \(n\))
\(|f\rangle \leftarrow R_z(-i\theta) |f \rangle \)
Uncompute \(|f\rangle \)
- Number of gates
- Number of physical qubits
- Effective space size
- Number of parameterized gates
- Depth
- Depth on LNN
- Energy span

What else are important?
Quality Measures
- Number of gates
- Number of physical qubits
- Effective space size
- Number of parameterized gates
- Depth
- Depth on LNN
- Energy span
What else are important?
Quality Measures

5 gates 1 parametrized
- Number of gates
- Number of physical qubits
- Effective space size
- Number of parameterized gates
- Depth
- Depth on LNN
- Energy span

What else are important?
Quality Measures
- Number of gates
- Number of physical qubits
- Effective space size
- Number of parameterized gates
- Depth
- Depth on LNN
- Energy span
What else are important?
Quality Measures


Linear Nearest Neighbour
All-to-All
- Number of gates
- Number of physical qubits
- Effective space size
- Number of parameterized gates
- Depth
- Depth on LNN
- Energy span

What else are important?
Quality Measures
Claim: FUNC-QAOA allows near-optimal circuit designs for various problems





Given: Graph with \(n\) nodes and \(K\) colors
Aim: Maximize (total weight of the edges) number of edges connecting different colors
(Weighted) Max-\(K\)-Cut

What is the best that can be achieved?

\(K\) colors \(\implies \log K\) bits to encode each color in binary
Number of qubits and effective space size
\(k^n\) possible assignments of colors to nodes
\(\implies\) smallest eff. space size is \(n \log K\)
\(n\) nodes \(\implies n\log K\) bits in total
011000
3 nodes colored blue green red

Has impact on the evolution!
\(\implies\) \(n \log K\) bits are needed to encode the solutions
00
01
10
Bounded by the number of degrees in the problem
For Max-\(K\)-Cut \(\implies\) number of possible edges \(n^2\)
Number of (parametrized) gates

Bounded by
number of gates / number of qubits
Depth (LNN)

Energy span

Minimum objective value: All nodes have different color
Maximum objective value: All nodes have the same color
\(\implies\) \(n^2\) possible edges
Has impact on number of measurements!
At least one cost depends siginificantly on K

State-of-the art
State-of-the art


X-QAOA
Mixer: X-mixer
Initial state: Product of equal superposition
Encoding: One-hot
3 nodes colored
blue green red
001
010
100
010-100-001
State-of-the art


XY-QAOA
Mixer: XY-mixer
Initial state: Product of W-state
Encoding: One-hot
Each \(b_i\) starts in an equal superspsition of one-hot states
State-of-the art

HOBO
Mixer: X-mixer
Initial state: Product of equal superposition
Encoding: Binary

\(|11\rangle \) not valid if there are only 3 colors
State-of-the art

Fuchs-QAOA
Mixer: X-mixer
Initial state: Product of equal superposition
Encoding: Binary
\(|10\rangle \) and\(|11\rangle \) represent same color if there are only 3 colors
Fuchs, Franz G., et al. "Efficient Encoding of the Weighted MAX-k-CUT on a Quantum Computer Using QAOA."
State-of-the art

Fuchs-QAOA
Very bad when \(K=2^k+1\)

Penalize states representing same colors
FUNC-QAOA for Max-\(K\)-Cut
FUNC-QAOA
Mixer: Grover-mixer
Initial state: Product of equal superposition of valid colors
Encoding: Binary

Each \(c_i\) starts in an equal superspsition of valid colors


Dependency on \(K\) disappears
FUNC-QAOA for Max-\(K\)-Cut
FUNC-QAOA




- We reached optimal quality measures
- We essentially dropped the dependency on \(K\)
- Fits very well NISQ requirements!
- Very important problem!
- We just took Fuchs idea and have simply chosen better initial state...
Let's go with a harder one
Travelling Salesman Problem!
YES
NO

Was it interesting?
Given: Graph with \(n\) nodes and cost between them
Aim: Find a tour with minimum total cost that visits each node exactly once
Travelling Salesman Problem

What is the best that can be achieved?


\(n\) cities \(\implies \log n\) bits to encode each city in binary
Number of qubits and effective space size
\(n!\) permutations
\(\implies\) eff. space size is \(\log n! \approx n \log n\)
\(\implies\) \(n\log n\) bits are needed to encode the solutions
00 01 10
\(n\) time points \(\implies n\log n\) bits in total
011000 Cities are visited in order 2-3-1

Bounded by the number of degrees in the problem
For TSP \(\implies\) \(n^2\) entries in the cost matrix
Number of (parametrized) gates

Bounded by
number of gates / number of qubits
Depth (LNN)

\(n\log n / n^2 \implies O(n/\log n) \)
Assuming each city is represented by a qubit and that it should interact with \(n-1\) other qubits, it is safe to assume \(O(n)\)
Energy span
Minimum objective value: \(n \cdot\) min cost edge
Maximum objective value: \(n \cdot\) max cost edge

State-of-the art

None of the encodings matches the "natural optimal" value
State-of-the art
Initial State:
Mixer:
Encoding:
X-QAOA XY-QAOA
Equal sup. One-hot
X-mixer XY-mixer
One-hot One-hot
GM-QAOA
Permutation
Grover-mixer
One-hot
HOBO
Equal sup.
X-mixer
Binary
State-of-the art

\(b_t\) encodes city visited at time \(t\)
Initial State:
Mixer:
Encoding:
X-QAOA XY-QAOA
Equal sup. One-hot
X-mixer XY-mixer
One-hot One-hot
GM-QAOA
Permutation
Grover-mixer
One-hot
HOBO
Equal sup.
X-mixer
Binary
State-of-the art
\(b_t\) encodes city visited at time \(t\)

Initial State:
Mixer:
Encoding:
X-QAOA XY-QAOA
Equal sup. One-hot
X-mixer XY-mixer
One-hot One-hot
GM-QAOA
Permutation
Grover-mixer
One-hot
HOBO
Equal sup.
X-mixer
Binary
State-of-the art
\(b_t\) encodes city visited at time \(t\)

Initial State:
Mixer:
Encoding:
X-QAOA XY-QAOA
Equal sup. One-hot
X-mixer XY-mixer
One-hot One-hot
GM-QAOA
Permutation
Grover-mixer
One-hot
HOBO
Equal sup.
X-mixer
Binary
State-of-the art
\(b_t\) encodes city visited at time \(t\)

Initial State:
Mixer:
Encoding:
X-QAOA XY-QAOA
Equal sup. One-hot
X-mixer XY-mixer
One-hot One-hot
GM-QAOA
Permutation
Grover-mixer
One-hot
HOBO
Equal sup.
X-mixer
Binary
State-of-the art
Time-to-city representation
Initial State:
Mixer:
Encoding:
X-QAOA XY-QAOA
Equal sup. One-hot
X-mixer XY-mixer
One-hot One-hot
GM-QAOA
Permutation
Grover-mixer
One-hot
HOBO
Equal sup.
X-mixer
Binary
We need to include cost matrix \(n\) times \(\implies O(n^3) gates \)
Time-to-city representation


City-to-city representation
This is used in MTZ-ILP, but with the cost of additional constraints to avoid subtours
City 4
City 2
\(W_{1}\)
\(W_{2}\)
\(W_{3}\)
\(W_{4}\)
\(W_{5}\)
\(W_{6}\)

We need to include each row of the cost matrix once
\(\implies O(n^2) gates \)
FUNC-QAOA for TSP
FUNC-QAOA
Mixer: Grover-mixer
Initial state: Product of equal superposition of valid cities
Encoding: Binary
Each \(b_t\) is an equal supersposition of valid cities



Permutation checking
Idea:
Count occurrence of each city in modulo 2
If they are not all 1, penalize
Cost of the route

Idea:
Switch from time-to-city to city-to city representation

FUNC-QAOA for TSP
GM-QAOA clearly better!
...but at a price
Numerics for TSP



The idea can be generalized, so far we managed to use it for
- Set Cover problem
- Integer Linear Problem (trade-off)
- Graph Isomorphism (trade-off in general, optimal for Euclidean graphs)

Very difficult for general graph!
Generalization
Now something different!

Factorization using FUNC-QAOA - Idea 1
\(\min.~~d_H(N\%p,0)\)
Notation: \(N\)-number to factorize, \(|p\rangle\) - quantum register with \(\log \sqrt{N}\) bits representing \(p\), \(\theta\) - optimized parameter
\(|r \rangle \leftarrow N \% |p\rangle \)
\(\forall i|r_i \rangle \leftarrow exp(-i\theta r_i)|r_i\rangle \)
Initialization of \(|p\rangle \): \(\frac{1}{N^{1/4}} \sum_{i=0}^{\sqrt{N}-1} |i\rangle \)
If \(p\) divides \(N\), then \(N\%p\) should be 0
Factorization using FUNC-QAOA - Idea 2
We want to find \(p\) and \(q\) such that \(N=pq\)
\(\min.~~d_H(N,pq)\)
Require: \(N\)-number to factorize, \(|p\rangle\) - quantum register with \(\log \sqrt{N}\) bits representing \(p\), \(|q\rangle\) - quantum register with \(\log \sqrt{N}\) bits representing \(q\), \(\theta\) - optimized parameter
\(|s \rangle \leftarrow |pq\rangle \)
\(|s \rangle \leftarrow |N\oplus s\rangle \)
\( \forall i|s_i\rangle \leftarrow exp(-i\theta s_i)|s_i\rangle \)
Initialization of \(|p\rangle \): \(\frac{1}{N^{1/4}} \sum_{i=0}^{\sqrt{N}-1} |i\rangle \)
Initialization of \(|q\rangle \): \(\frac{1}{N^{1/4}} \sum_{i=0}^{\sqrt{N}-1} |i\rangle \)
\(d_H\): Hamming distance
Factorization using FUNC-QAOA - Idea 3
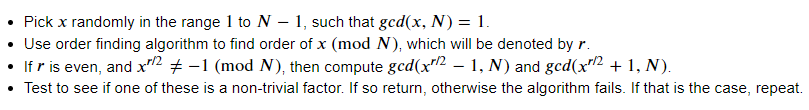
Shor's Algorithm
Idea: Given \(x\) is coprime with \(N\), find \(r\) such that \(r\) is the smallest integer satisfying
- \(x^r = 1 \mod N\)
- \(x^{r/2} \neq -1 \mod N\)
- \(r\) is even
Under Progress
Factorization using FUNC-QAOA - Idea 3
\(min.~~r + A[x^r \neq1 \mod N] \)
\(|s \rangle \leftarrow x^{|r\rangle} \mod N \)
if \( |s \rangle!= 1\) then
\(|flag \rangle \leftarrow |1\rangle \)
\( |flag \rangle \leftarrow R_z(-i\theta A) |flag \rangle \)
Initialization of \(|r\rangle \): \(\frac{1}{\sqrt{N/2}} \sum_{i=1}^{N/2} |2i\rangle \)
Require: \(N\)-number to factorize, \(|r\rangle\) - quantum register with \(\log N\) bits representing \(r\), x - an integer that is coprime with \(N\), \(\theta\) - optimized parameter, \(A\) - penalty parameter
\( |r \rangle \leftarrow exp(-i\theta r) |r \rangle \)
Under Progress
Factorization using FUNC-QAOA - Idea 4
Fermat's Factorization Method
If \(N=a^2-b^2\), then \(N=(a-b)(a+b)\).
\( (a-b) \) and \( (a+b)\) are factors of \(N\)
Idea: Find integers \(a\) and \(b\) such that \(N=a^2-b^2\).
Under Progress
Factorization using FUNC-QAOA - Idea 4
\(min.~~d_H(N,a^2 - b^2)\)
Require: \(N\)-number to factorize, \(|a\rangle\) - quantum register with \(\log N\) bits representing \(a\), \(|b\rangle\) - quantum register with \(\log N\) bits representing \(b\), \(\theta\) - optimized parameter
\(|s \rangle \leftarrow |a\rangle ^2 \)
\(|t \rangle \leftarrow |b\rangle ^2 \)
\(|r_i \rangle \leftarrow N \oplus (|s \rangle -|t \rangle) \)
\( \forall i|r_i \rangle \leftarrow exp(-i\theta r_i) |r_i \rangle \)
Initialization of \(|a\rangle \): \(\frac{1}{\sqrt{N}} \sum_{i=1}^{N} |i\rangle \)
Initialization of \(|b\rangle \): \(\frac{1}{\sqrt{N}} \sum_{i=1}^{N} |i\rangle \)
Under Progress
-
Bärtschi, Andreas, and Stephan Eidenbenz. "Grover mixers for QAOA: Shifting complexity from mixer design to state preparation." 2020 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2020.
-
Fuchs, Franz G., et al. "Efficient Encoding of the Weighted MAX-\(K\)-CUT on a Quantum Computer Using QAOA." SN Computer Science 2.2 (2021): 1-14.
-
Glos, Adam, Aleksandra Krawiec, and Zoltán Zimborás. "Space-efficient binary optimization for variational quantum computing." npj Quantum Information 8.1 (2022): 1-8.
-
Tabi, Zsolt, et al. "Quantum optimization for the graph coloring problem with space-efficient embedding." 2020 IEEE International Conference on Quantum Computing and Engineering (QCE). IEEE, 2020.
-
Wang, Zhihui, et al. "X y mixers: Analytical and numerical results for the quantum alternating operator ansatz." Physical Review A 101.1 (2020): 012320.
-
Lucas, Andrew. "Ising formulations of many NP problems." Frontiers in physics (2014): 5.
-
Farhi, Edward, Jeffrey Goldstone, and Sam Gutmann. "A quantum approximate optimization algorithm." arXiv preprint arXiv:1411.4028 (2014).
-
Peruzzo, Alberto, et al. "A variational eigenvalue solver on a photonic quantum processor." Nature communications 5.1 (2014): 1-7.