My Quantum Journey

Özlem Salehi

11.10.2022

Qiskit Quantum Explorers
Quantum Women Invited Talk Series

B.S. in Mathematics
Boğaziçi University, Turkey, 2011

M.S. in Computer Engineering
Boğaziçi University, Turkey, 2013

Ph.D. in Computer Engineering
Boğaziçi University, Turkey, 2019

Teaching assistant
Boğaziçi University, Turkey, 2011 - 2019

Instructor
Özyeğin University, Turkey, 2019 - 2021

Postdoctoral researcher
Institute of Theoretical and Applied Informatics Polish Academy of Sciences, Poland, 2021 -

RESEARCH

Main Focus: Solving optimization problems using quantum computing in the NISQ era

Two main approaches

Quantum Annealing

Quantum Approximate Optimization Algorithm

Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.

Quantum Annealing

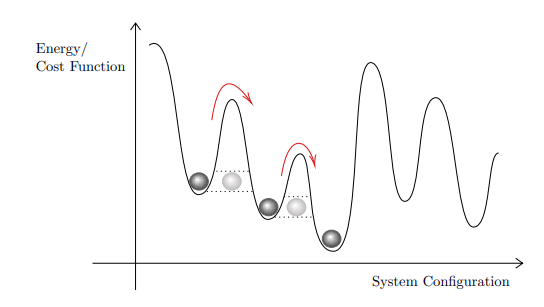
Follows the adiabatic evolution defined through time-dependent Hamiltonian

Adiabatic Quantum Computing

$H(t) =\frac{1-t}{\tau} \:H_{\rm mix} + \frac{t}{\tau}\: H_c$

Slow evolution during time $\tau$

Quantum Adiabatic Theorem: A quantum system that starts in the ground state of a time-dependent Hamiltonian, remains in the in the instantaneous ground state provided the Hamiltonian changes sufficiently slowly.

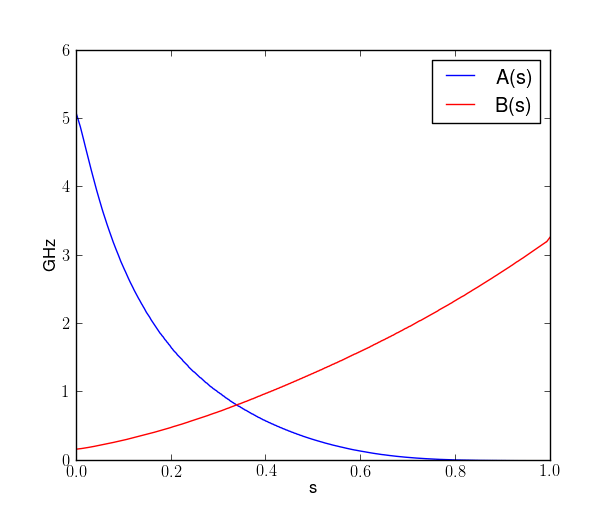
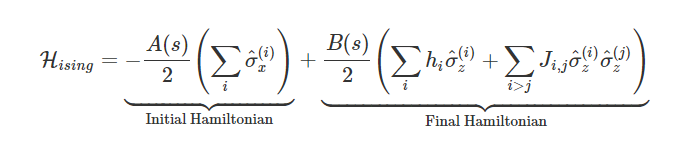
Quantum Annealing

Implemented by D-Wave quantum annealers

Some conditions of AQC are relaxed in QA resulting in a heuristic algorithm

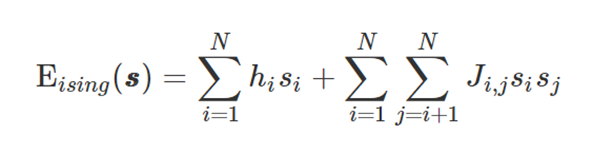
Quadratic Uncostrained Binary Optimization (QUBO)

\min.~f(x_1,x_2) = 5x_1 + 9x_2 -6x_1x_2

$x_1 = 0$ and $x_2 = 0$: $f(0,0) = 5\cdot 0 + 9\cdot 0 - 6\cdot 0\cdot 0 = 0$
$x_1 = 0$ and $x_2 = 1$: $f(0,1) = 5\cdot 0 + 9\cdot 1 - 6\cdot 0\cdot 1 = 9$
$x_1 = 1$ and $x_2 = 0$: $f(1,0) = 5\cdot 1 + 9\cdot 0 - 6\cdot 1\cdot 0 = 5$
$x_1 = 1$ and $x_2 = 1$: $f(1,1) = 5\cdot 1 + 9\cdot 1 - 6\cdot 1\cdot 1 = 8$

$\displaystyle \min.~\sum_{i} Q_{i,i} x_i + \sum_{i<j} Q_{i,j}x_i x_j $

Constrained problem:

$\min.~~ f(x_1,x_2)$
$s.t.~~~~x_1+x_2\geq 1$

QUBO for TSP

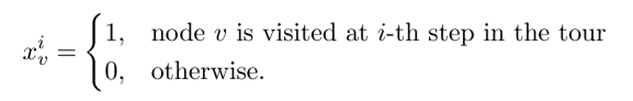
1, node $i$ is visited at step $t$ in the tour

0, otherwise

$\displaystyle \sum_{i=0}^{n-1} b_{t,i}=1$ for all $t=0,\dots,n-1$

City $i$ is visited

exactly once

$\displaystyle \sum_{t=0}^{n-1} b_{t,i}=1$ for all $i=0,\dots,n-1$

At time $t$ exactly one city is visited

Constraints

Objective

If both variables are 1, this means $ij$ is traversed at time $t$

$b_{t,i}$

$\displaystyle \sum_{\substack{i,j=0 \\ i\neq j }}^{n-1} W_{ij} $

$\displaystyle \sum_{t=0}^{n-1}b_{t,i}b_{t+1,j}$

Express your problem as a
Quadratic
Unconstrained
Binary
Optimatization

problem

Solving a Problem Using QA

Obtain the equivalent Ising model

Use QA to find the variable assignment that minimizes energy

$\displaystyle \sum_{i} Q_{i,i} x_i + \sum_{i<j} Q_{i,j}x_i x_j $

$x_i \mapsto \frac{s_i+1}{2}$

$\displaystyle \sum_{i} h_i s_i + \sum_{i<j} J_{i,j}s_i s_j $

Quantum annealing - Pros and Cons

Embedding problem
Noise - error correction?

DISADVANTAGES

Larger number of qubits
Aims at optimization problems - real-world applications

ADVANTAGES

Considered Problems

Travelling Salesman with Time Windows

Music generation

Music reduction

Test vehicle optimization

Railway dispatching problem

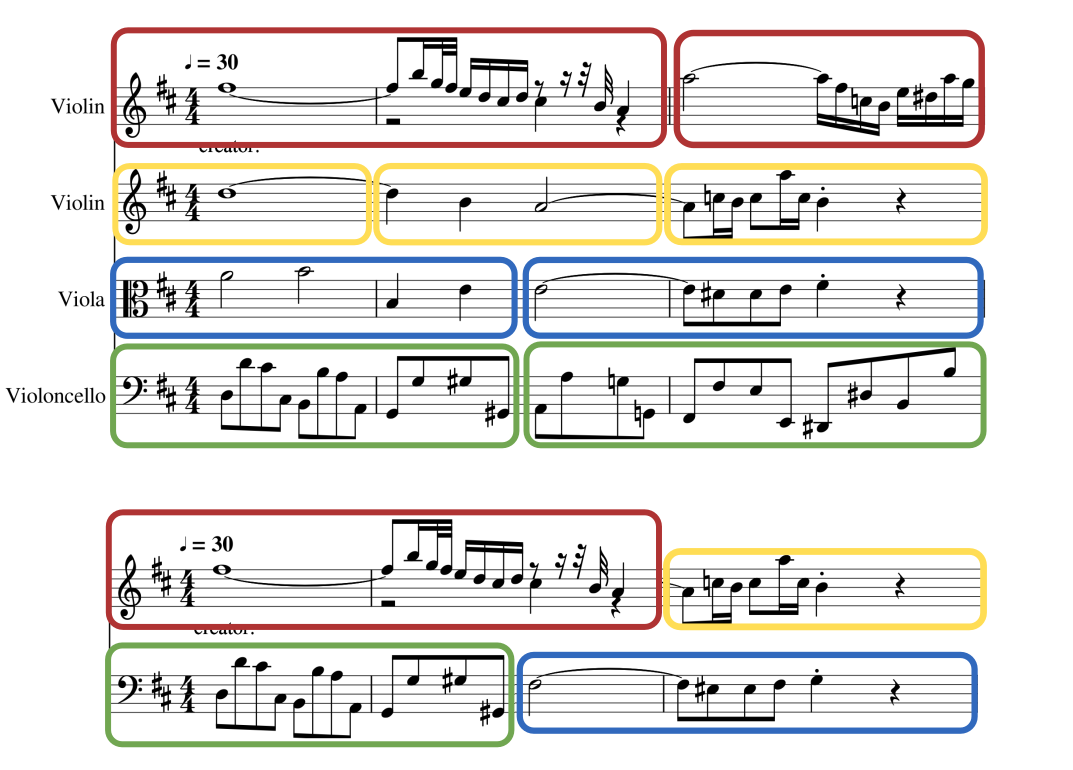
Travelling Salesman Problem with Time Windows

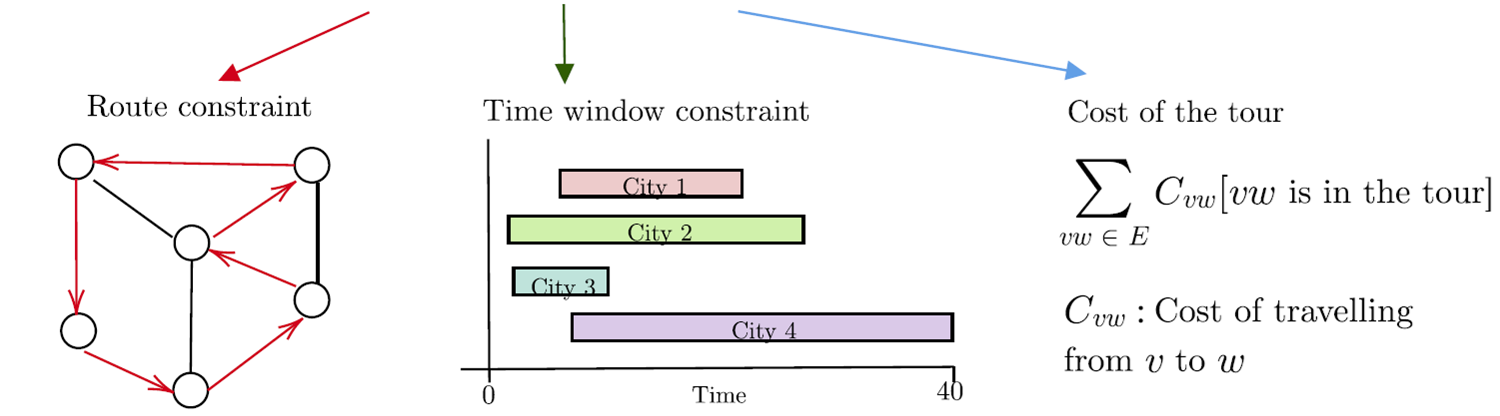
Constraints

Objective

Salehi, Ö., Glos, A. and Miszczak, J.A., 2022. Unconstrained binary models of the travelling salesman problem variants for quantum optimization. Quantum Information Processing, 21(2), pp.1-30.

Aim: Find a closed route with minimum cost that visit each city exactly once obeying each city's time window.

Music Generation

Aim: Generate a melodic sequence of pitches

Pitches

that is plausible to the ear!

How to formulate this as an optimization process?

Arya, A., Botelho, L., Cañete, F., Kapadia, D., & Salehi, Ö. (2022). Music Composition Using Quantum Annealing. to appear in Quantum Computer Music: Foundations, Methods and Advanced Concepts : Springer, 2022.

Music Reduction

Aim: Given a music piece with T tracks, obtain a new music with M<T tracks keeping the characteristics of the song as much as possible

Test-vehicle optimization

Glos, A., Kundu, A. and Salehi, Ö., 2022. Optimizing the Production of Test Vehicles using Hybrid Constrained Quantum Annealing. arXiv preprint arXiv:2203.15421.

Aim: Given a list of tests, requiring cars with certain features, find the minimum number of cars that cover the tests and obey the configuration rules

Railway Dispatching Problem

Domino, K., Kundu, A., Salehi, Ö. and Krawiec, K., 2022. Quadratic and higher-order unconstrained binary optimization of railway rescheduling for quantum computing. Quantum Information Processing, 21(9), pp.1-33.

Aim: Reduce delay propagation in railway systems in case of disruptions by rescheduling and rerouting

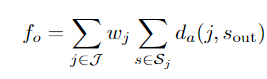
Objective: Minimize weighted additional delay

Constraints reflect minimal headway between trains, minimal stay on stations, station/track occupation, and rolling stock circulation on double-track and multi-track lines.

Two main approaches

Quantum Annealing

Quantum Approximate Optimization Algorithm

Zhou, Leo, et al. "Quantum approximate optimization algorithm: Performance, mechanism, and implementation on near-term devices." Physical Review X 10.2 (2020): 021067.

Quantum Approximate Optimization Algorithm

Quantum Approximate Optimization Algorithm (QAOA)

For the gate based model

$\gamma_i$ and $\beta_i$ optimized by external classical procedure

$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+^n\rangle $$

Can be viewed as a trotterization of AQC

Quantum Approximate Optimization Algorithm (QAOA)

$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |+^n\rangle $$

Typical initial state

$-\sum_i X_i$ s.t. eigenstate of $X$ is $|+\rangle$

$2p$ parameters required for $p$ layers

Expectation $\langle \gamma,\beta| H_c | \gamma, \beta \rangle $ is approximated by measurement in the computational basis

Quantum Alternating Operator Ansatz (QAOA+)

$$|\gamma,\beta\rangle = \prod_{i=1}^p \exp(-\mathrm{i} \beta_iH_{\rm mix})\exp(-\mathrm{i} \gamma_iH_c) |s\rangle $$

Subspace of the full Hilbert space containing all feasible states

Should preserve the space

Example: One-hot states and XY Mixer

1/\sqrt{3} ~ ( |100\rangle + |010\rangle +|001\rangle)

\sum_{i=1} X_iX_{i+1} + Y_iY_{i+1}

$b_{0,0}$

$b_{0,1}$

$b_{0,2}$

$b_{1,0}$

$b_{1,1}$

$b_{1,2}$

$b_{2,0}$

$b_{2,1}$

$b_{2,2}$

$t=0$

$t=1$

$t=2$

1/\sqrt{8} ~ ( |000\rangle + |001\rangle + \dots + |111\rangle)

1/\sqrt{3} ~ ( |100\rangle + |010\rangle +|001\rangle)

Botelho, L., Glos, A., Kundu, A., Miszczak, J. A., Salehi, Ö., & Zimborás, Z. (2022). Error mitigation for variational quantum algorithms through mid-circuit measurements. Physical Review A, 105(2), 022441.

Error mitigation through mid-circuit measurement

Ideally, quantum state of the system should be a superposition of valid states throughout the evolution.

For TSP with one-hot encoding, product of one-hot states

Idea: Detect and remove unvalid states during the evolution

Postselection by filtering

If $|s\rangle$ is not a valid state, ancilla will no longer be in $|0\cdots0\rangle$ state

$\implies$ Measure ancilla and continue if it is all 0

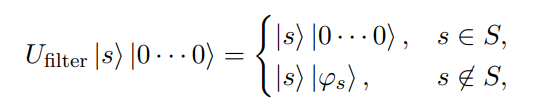
$k$-hot states: Count number of 1's
Domain wall encoding: Check consecutive bit pairs
Binary encoding: Check if encoded number exceeds maximum possible value

1000, 1100, 1110, 1111

1000, 0100, 0010, 0001

00, 01, 10, 11

Postselection by compression

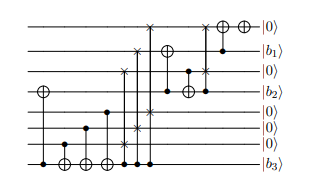
For one-hot states, apply the conversion circuit from one-hot to binary

Check if bits are 0

Near-Optimal Circuit Design for QAOA

We introduce an alternative way for implementing QAOA that allows reaching near-optimal cost metrics

Idea: Start with a classical pseudo-code function and implement it using a quantum circuit

State of the art

$b_i \leftarrow \frac{1-s_i}{2}$

Start with a
QUBO or HOBO

Get the corresponding Ising model

Implement each term in the expression

How to implement QAOA?

QUBO: $\min.~\displaystyle \frac{1}{2}\sum_{(i,j) \in E}2x_ix_j - x_i - x_j $

Ising model: $\min.~ \displaystyle \frac{1}{2}\sum_{(i,j) \in E} (s_is_j-1)$

$\implies \min. \displaystyle \sum_{(i,j) \in E} s_is_j $

$\displaystyle \sum_{(i,j) \in E} Z_iZ_j $

Corresponding Hamiltonian:

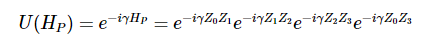
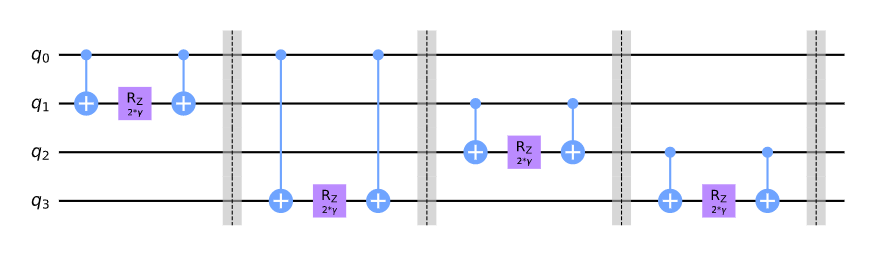
$x_i \leftarrow \frac{1-s_i}{2}$

https://qiskit.org/textbook/ch-applications/qaoa.html

$b_i \leftarrow \frac{1-s_i}{2}$

$H = -\prod_{i=1}^n b_i$

$b_i \in \{0,1\}$

Exponential number of CNOT gates!

Exponential number of terms !

$H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)$

$s_i \in \{-1,1\}$

State of the art implementation

$O(n^2)$ gates on LNN!

$H = -\frac{1}{2^n} \prod_{i=1}^n (1-s_i)$

$s_i \in \{-1,1\}$

Yet, there exists another efficient circuit

Claim: FUNC-QAOA allows near-optimal circuit designs for various problems

New Idea: Start with a classical pseudocode function

FUNC-QAOA

FUNC-QAOA for TSP

Mixer: Grover-mixer
Initial state: Product of equal superposition of valid cities
Encoding: Binary

\frac{1}{\sqrt{3}} (|00\rangle + |01\rangle + |10\rangle)

Each $b_t$ (which represents in binary city visited at time $t$) is initialized as the equal superposition of valid cities

Permutation checking

Idea:

Count occurrence of each city in modulo 2
If they are not all 1, penalize

Cost of the route

Idea:

Switch from time-to-city to city-to-city representation

QUESTIONS